gqajuin1.html

quebecium Suivant http://www.lisulf.quebec/gqajuin2.html

Traduction interdite Tous droits de traduction réservés

En premier lieu, je présente le Tableau périodique des éléments, et je procède à l'améliorer. Par une analyse arithmétique et géométrique, je fais apparaître d'importantes symétries d'ordre quatre qui existent dans la mise en ordre des atomes entre eux. Je confirme ces résultats par une discussion originale sur les atomes irréguliers. J'essaierai, dans un travail qui suivra, d'interpréter les symétries de la classification par les symétries de l'atome qui sont associées aux cônes de précession des moments cinétiques propres et orbitaux.*

*Paul Verlaine (1844-1896), Prince des poètes en 1894.

"De la musique avant toute chose,

Et pour cela préfère l'Impair"

Art poétique, 1874

*L'impair trois dans l'alexandrin prête à sa mise en carré. Fig. 1, 0.

Fig. 1, 0 . Racine, Phèdre.

•

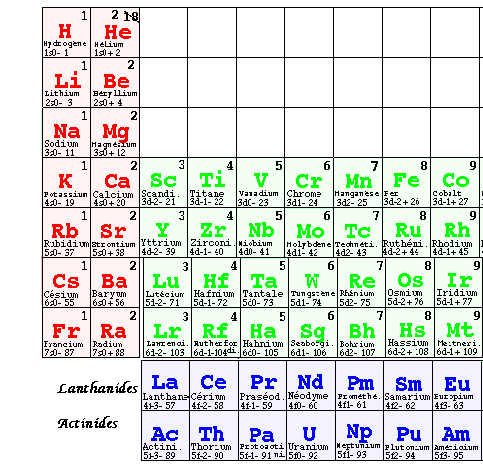
Tous les étudiants de chimie ont l'occasion d'apercevoir ce Tableau, dû à Mendeleev, Seaborg et plusieurs autres. Il énumère, avec alinéas, les éléments ordonnés selon les valeurs de Z, numéro atomique, rangés par périodes horizontales et colonnes verticales telles qu'en principe, les propriétés chimiques et physiques dans une colonne se ressemblent dans les périodes successives. Fig. 2.,51ter.

Mon analyse porte principalement sur les propriétés électroniques des atomes constituant les éléments et recherche la symétrie de leurs représentations. Je considère au départ le Tableau périodique, tel qu'il apparaît dans la figure 2, et je le transforme d'abord en un Tableau périodique remanié (Fig. 4, 51bis). On ne peut pas innover sans changer, aussi l'aspect traditionnel en rangées et colonnes va disparaître. Pour cette raison, mieux vaut-il appeler le nouveau tableau autrement que "périodique". même si les périodes y sont présentes. Ce qui va être conservé est comme suit.

Le carrelage de cases carrées, comparable à un échiquier, où les pièces sont placées selon un plan défini.

Le contenu des cases individuelles.

Je cherche à améliorer le tableau mentionné. Une nouveauté majeure est l'utilisation de deux dimensions pour la représentation des périodes. Les périodes ne sont plus des rangées linéaires de cases. Chaque période occupe des cases appartenant à au moins deux rangées horizontales, de sorte que la distinction entre rangée et colonne n'est plus fondamentale.

J'appelle le système présidant à la mise en ordre nouvelle Système du Québécium pour des raisons historiques, parce que la première version du tableau nouveau finissait avec l'élément spéculatif 118 que j'ai baptisé québécium, il était le terme de la dernière période connue. Le nouveau tableau pourrait s'appeler pour cette raison Tableau du Québécium.

Une autre raison plus fondamentale s'ajoute aux raisons historiques. C'est que la formule électronique du québécium contient celle de tous les éléments connus. La formule du québécium comprend 118 termes numérotés de 1 à 118. Il suffit, pour obtenir la formule de l'élément Z, d'enlever de celle du québécium les termes allant de 118 à Z+1. Un tableau qui contient tous les éléments, qu'il s'agisse du Tableau périodique des éléments ou du tableau nouveau ou d'un autre quelconque, est en quelque sorte le tableau de ce que contient le québécium. Il est le tableau de tous les éléments que le québécium contient virtuellement. Fig. 3. 71.

Fig. 2, 51ter. Tableau périodique des éléments. Sept périodes occupent autant de rangées, en plus des lanthanides et des actinides. Les colonnes sont verticales. La place de He est sujette à discussions. Du point de vue chimique, He appartient à la colonne 18 comme Ne et les autres gaz rares. Je préfère le placer dans la colonne 2 à cause de sa configuration électronique. Les colonnes de 1 à 18 sont données par l'Union internationale de chimie pure et appliquée UICPA. Ailleurs, je fais usage des numéros 19 à 32 pour les lanthanides et les actinides. Afin de ne laisser aucune case vide dans mes tableaux, j'ai ajouté les éléments spéculatifs 119 et 120, qui sont le début d'une huitième période spéculative.

Le présent tableau contient la liste complète et ordonnée selon la valeur de Z de tous les éléments que je considère plus loin. La même liste, lue en sens inverse en commençant par Qb 118 donne la formule électronique du québécium. Voyez cette formule, figure 3, 71.

Le nouveau tableau n'a pas qu'un contenu, il a une forme et dans cette forme, on verra que les cases de contenu comparable tracent des carrés. Le carré prédomine. Sa forme présente les symétries du carré, d'ordre quatre. Pour cette raison, on serait justifié d'appeler le nouveau tableau des éléments "Tableau quadratique des éléments"

Le Tableau périodique, à la vérité, possède le nécessaire à la source d'un tableau quadratique puisque, sans addition sinon celle d'une organisation mutuelle, on en déduit le tableau quadratique. Il est donc un peu quadratique lui-même (disons crypto-quadratique). Par ailleurs, ses cases sont carrées; mais elles sont organisées selon des périodes rectilignes successives et il n'a aucune bidimensionnalité à l'intérieur des périodes.

Fig.3, 71. Formule (électronique) du québécium. Le québécium contient virtuellement tous les éléments connus. On les obtient par une synthèse soustractive. Pour obtenir la formule de l'élément Z, on on enlève de la formule du québécium ci-dessus les termes de 118 à z+1. 3I2007

N. B. Ce sont des formules nominales, identiques aux formules réelles dans la plupart des éléments, qui sont réguliers. On connaît 19 éléments irréguliers, dont l'examen est instructif, suggérant la réalité d'une classification quadratique des éléments. Voir plus loin.

N. B. Le tableau nouveau a connu plusieurs versions. Il a évolué depuis la toite première d'entre elles, que j'ai abandonnée. C'était une version à 118 éléments, calquée respectueusement sur le tableau périodique habituel, avec deux cases vides après He. Suivit une version primitive qui se loge dans une demi-ellipse; puis une version qui tient dans une ellipse et une autre, dans un quart d'ellipse. Ce sont des versions 2D. Il y a en outre des versions 3D, occupant les trois dimensions.

Voici mes 4 étapes vers le nouveau tableau dans la présentation originale que voici.

1. Tableau périodique des éléments remanié.

2. Demi sous-blocs et demi sous-couches en nombres impairs dans les périodes.

3. Réflexions sur les équerres. Représentation d'un impair par une équerre équilatère.

4. Un tableau quadratique.

Dans une première étape du processus qui donnera finalement le tableau nouveau, j'ai remanié le tableau de la figure 1 et le résultat, que j'appelle Tableau périodique remanié, apparaît à la figure 3.51bis. L'ordonnance ainsi réalisée a le grand intérêt d'être davantage symétrique.

Le remaniement est obtenu par deux translations à angle droit. Par une première translation horizontale, je place les colonnes 1 et 2 à droite de la dernière et dix-huitième. Par une deuxième translation qui est verticale, je déplace les mêmes colonnes 1 et 2 d'une rangée vers le haut. Fig. 3, 51bis.

Cela revient à faire des éléments des colonnes 1 et 2 les derniers éléments des périodes à partir de de celle contenant les éléments 5, 6 etc, et non plus les premiers. Ils suivent immédiatement les éléments de la colonne 18 qui sont les gaz rares. Les éléments Z = 1 à 4 apparaissent comme un groupe distinct suggérant deux périodes isolées marquant le début du tableau des éléments.

L'ordonnance ainsi réalisée n'est pas une innovation de ma part. Elle est exactement celle proposée par un anticipateur peu remarqué, Charles Janet de Beauvais en 1927. Il anticipait quant aux deux extrémités du tableau des éléments. Pour ce qui est du début, il suggérait deux périodes courtes, ce que je propose ici explicitement; pour ce qui est de la fin, il suggérait deux périodes longues, dont l'existence n'a été définitivement admise qu'après les travaux de Seaborg vers 1945.

ISBN B0000DQ0QX

Ce qui est une innovation de ma part suit.

Fig. 4, 51bis. Tableau périodique des éléments remanié (à la manière de Janet ) en huit périodes et arrété à l'élément 120. Quarante demi sous-couches. Ce tableau, aussi bien que le précédent Fig.2, est tout entier composé de demi sous-couches. Elles sont au nombre de 40 et elles sont mises en évidence ici. Dans ce tableau, les périodes se présentent par paires ayant des blocs égaux en longueur : 2, 8, 18 et 32 cases. J'appelle strates ces paires.

"Une demi sous-couche compte un nombre impair d'éléments".

J'examine la structure des périodes.

La suite des éléments dans une période du tableau tel que remanié forme un bloc ininterrompu. Il se fragmente en sous-blocs, chaque sous-bloc étant une sous-couche, où la valeur du quantum de moment cinétique orbital l reste constant : l = 0, 1, 2 ou 3. Une couche est la suite des éléments ayant la même valeur du quantum principal n. Sous-blocs et sous-couches se fragmentent à leur tour en deux moitiés égales, selon la valeur du nombre s, égale à - ou +. La moitié + suit immédiatement la moitié -. Il y a donc huit sortes de demi sous-blocs et de demi sous-couches, comme suit.

0-, 0+; 1-, 1+; 2-, 2+; 3-, 3+

Le paramètre spin correspond au moment cinétique propre de l'électron. Une demi sous-couche est identifiée complètement par les trois nombres quantiques n, l, s. Elle est composée d'un nombre restreint d'éléments et ce nombre est un impair. Il y a un élément par case et une case dans une demi sous-couche est identifiée complètement par un quatrième nombre quantique m, quantum magnétique,

"Le nombre d'éléments, égal au nombre des valeurs de m dans une demi sous-couche, est 1, 3, 5 ou 7." On l'appelle dégénérescence, il est égal à 2l+1.

Une manière d'illustrer la genèse des nombres m est la règle du 2l+1. C'est de considérer l comme un vecteur de valeur absolue Ã[l(l+1)] doué d'un moment magnétique proportionnel à cette valeur. On suppose que l'atome possède un champ magnétique qui oriente ce vecteur. Les orientations possibles sont celles assurant une projection au plus égale à l en valeur absolue, parmi les valeurs 0, ±1, ±2, ±3 etc C'est en somme ce qui se passe dans l'effet Zeeman. Le nombre de ces projections est égal à la dégénérescence. Fig. 5, 58.

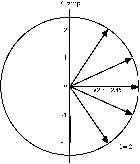
Fig. 5, 58. Au nombre quantique l = 2, on associe un vecteur de valeur absolue Ã[l(l+1)] = Ã(2.3) = 2,45.

Dans un champ magnétique qu'on imagine exister dans un atome, ce vecteur peut prendre les orientations assurant une projection de valeur absolue nulle ou entière inférieure à 2,45. Il y a cinq telles projections, qui sont les valeurs de m : -2, -1, 0, 1, 2. Cinq est la dégénérescence du nombre l = 2. La dégénérescence d'un nombre entier l est nécessairement égale à un impair.

Dans un carrelage, trois cases contigües non alignées sont la représentation graphique de l'impair trois. Elles forment une équerre équilatère dont les bras valent l'unité. Il en est semblablement pour cinq, sept etc. Je confonds dans mon langage l'impair k et l'équerre ayant k cases. Une équerre équilatère a une case centrale ou charnière et des cases latérales qui sont ses bras. Si les bras sont nuls, l'équerre n'a que la case charnière. Une équerre équilatère dont chaque bras vaut l (nécessairement entier), possède k = 2l+1 cases. Je confonds de plus l nombre quantique de moment cinétique orbital et l nombre de cases dans un bras de l'équerre.

k = 2l+1

Impairs et équerres. Un impair k se figure par une équerre de cases symétrique dans le carrelage que je me suis donné. Dans une équerre équilatère ou symétrique, les bras sont égaux. Fig. 6 59.

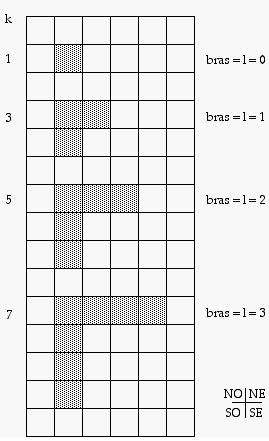
Fig. 6, 59. Nombre impair = équerre k.

Équerre k = 2l+1, l = nombre quantique de moment cinétique orbital.

Je vois dans les considérations arithmétiques et géométriques qui précèdent la suggestion de remplacer, dans le tableau périodique remanié, les demi sous-couches rectilignes par des équerres de cases occupant deux dimensions. Le tableau de quarante alignements unidimensionnels sera remplacé par un ou plusieurs tableaux carrelés contenant quarante équerres bidimensionnelles.La nature même des choses réclame de moi cette démarche, susceptible de me conduire à mieux connaître des aspects de la nature des choses.

On gagne, dans la solution de certains problèmes, à utiliser une géométrie de représentation plutôt qu'une autre, cartésienne, sphérique, circulaire, hexagonale ou triangulaire. Dans le cas de la classification des atomes, je propose qu'on pourrait gagner à utiliser, comme géométrie de représentation, celle des équerres et des symétries d'ordre quatre, suggérée par la théorie des moments cinétiques orbitaux et de la théorie du spin qui est un moment cinétique propre égal à 1/2.

Il y a plusieurs manières de disposer entre elles quarante équerres. Voici quelques propriétés des équerres équilatères pouvant nous guider.

Une équerre (équilatère) dans un carrelage est un objet mathématique avec ses propriétés et ses contraintes.

Fig. 7, 60. Quatre couronnes résultant de l'assemblage exact de quatre équerres semblables.

Composition. Une équerre k contient un nombre impair k de cases, égal à 1, 3, 5 etc, Chacun de ses bras contient un nombre de cases égal à l = 0, 1, 2 etc, avec k = 2l+1.

Similitude. Deux équerres sont semblables si elles ont les mêmes valeurs de k. Elles sont superposables par translation et rotation dans le plan.

Orientations et rotations. Une équerre a l'une de quatre orientations, différant l'une de l'autre par une rotation multiple entier de 90o. L'orientation est celle pointée par l'équerre vue comme une flèche, sur la rose des vents : NO, SO, SE, NE. L'équerre de bras nuls l = 0, k = 1, a ces quatre orientations indifféremment.

Association exacte : couronnes. Quatre équerres semblables ayant chacune des orientations possibles s'associent exactement en une couronne (quadrangulaire, fermée). La couronne d'équerres de bras nuls, k = 1, est pleine. Les autres, k > 2, ont un vide qui reçoit exactement une ou plusieurs couronnes emboîtées. Fig. 7, 60.

Inscription. Une équerre k s'inscrit dans un carré de côté (k+1)/2.

Inscription exacte de K équerres semblables k dans un carré. Soit K équerres semblables assemblées exactement, K = 2, 3, 4. Le carré le plus petit pouvant les circonscrire exactement a pour côté k+1.

Fig. 8. Carré circonscrit exactement à une équerre; à l'assemblage exact de K équerres semblables, avec K = 2, 3 ou 4. Carré circonscrit à l'assemblage en diagonale symétrique de deux équerres semblables

Il est le même pour K = 2, 3 ou 4. Il est le même pour l'assemblage en diagonale symétrique de deux équerres semblables. Fig. 8.

Association : carrés d'impairs. La suite des équerres (dissemblables) s'emboîte exactement et trace un carré totalisant la puissance deux de leur nombre. Fig. 9, 61ter.

Suite d'équerres, nombre d'équerres. Une suite d'équerres dont la plus grande est k, renferme (k+1)/2 équerres.

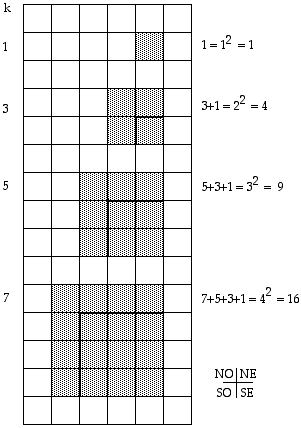
Fig. 9, 61ter. La suite des impairs est égale à la puissance deux de leur nombre.

Et voilà Fig. 12, 52 un tableau quadratique consécutif et conforme aux considérations des étapes 1, 2 et 3 qui précèdent. Certaines de ses dispositions sont imposées, d'autres relèvent de mon arbitraire. Voyons d'abord les dispositions imposées.

Deux périodes prises à la fois égale une strate. Un caractère frappant du Tableau remanié est sa dualité : les périodes s'y présentent en groupes de deux ayant même longueur et même structure. Les cases respectives de la deuxième période répètent la formule nlms de celles de la première période avec addition de l'unité à n.

Première période : ......nlms

Deuxième période : (n+1)lms

Il est difficile de voir là effet du hasard et pures coïncidences numériques et d'échapper à cette sorte de symétrie. Au contraire, il est naturel de voir là une invitation à grouper les périodes deux par deux et d'y donner suite. Dans la perspective d'une recherche de symétrie, le résultat est encourageant puisque les groupes successifs, que j'appelle des strates, sont tous des carrés exacts d'entiers et reflètent la suite des pairs et celle des carrés des entiers un, deux, trois et quatre.

Strate 1 = 4 = 2² = 4 X1²

Strate 2 = 16 = 4² = 4X2²

Strate 3 = 36 = 6² = 4X3²

Strate 3 = 64 = 8² = 4X4²

Les moitiés de strates c'est-à-dire les périodes ne sont pas des carrés d'entiers.

Une période de la strate 1 = 2

Une période de la strate 2 = 8

Une période de la strate 3 = 18

Une période de la strate 3 = 3²

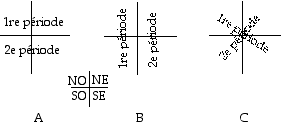
Fig. 10, 51 quater. Affectation des quadrants aux périodes 1re et 2e dans une strate.

En revanche, les quarts de strates c'est-à-dire les moitiés de périodes sont des carrés d'entiers.

Une moitié de période de la strate 1 = 1 = 1²

Une moitié de période de la strate 2 = 4 = 2²

Une moitié de période de la strate 3 = 3²

Une moitié de période de la strate 3 = 4²

La représentation d'une strate sera naturellement un carré et par symétrie il est à peu près obligatoire que l'affectation de son domaine soit répartie selon ses quatre quadrants et que deux soient dévolus à la première période de la strate, et les deux autres, à la deuxième période.

Ici commencent choix et décisions arbitraires. Le premier quadrant de chaque période sera de spin - et le deuxième, de spin +. Voyons les autres dispositions à choisir arbitrairement Trois possibilités principales se présentent quant à l'affectation des quadrants aux périodes. Fig. 10, 51quater. J'exclus B parce que j'affecte l'ouest au spin - et l'est au spin + et je préfère C qui fait participer nord et sud à chaque période.

Poursuivons et voyons donc comment meubler les quadrants.

Quantum l. Valeur de l, quantum de moment cinétique orbital. Il n'y a pas de case centrale dans une strate, mais un centre ponctuel. J'attribue un paramètre distance du centre d = 0 aux quatre cases les plus rapprochées du centre, puis les paramètres 1, 2, 3 aux cases des couronnes plus éloignées. Cette distance se trouve égale à l = k-1 tel que dans la discussion plus haut sur la géométrie des impairs et des couronnes. J'affecte les cases des couronnes l à l'hébergement des atomes ayant le quantum l. Avec le jeu de couleurs choisi, les cases des couronnes RJVB rouge, jaune, vert et bleu reçoivent respectivement les éléments de quantum l = 0, 1, 2 et 3, de symboles littéraux souvent pratiqués s, p, d, f, ce qui fut une notation spectroscopique avant d'être interprété dans la théorie des vecteurs moments cinétiques orbitaux. (Notez qu'il existe une certaine proportionnalité entre les distances probables d'un électron au centre de l'atome et les présentes distances d = l = k-1). Fig. 11, 67.

Quantum m. Le quantum m correspond à un angle de rotation désignant l'une des cases à l'intérieur de la couronne l à mesure qu'on garnit le quart de couronne. Par symétrie, les rotations sont choisies soit directes, i. e. dans le sens des aiguilles d'une montre, soit anti, dans le sens opposé. Voyez le plan universel. Fig. 11, 67.

Plan universel. Il se trouve que l'occupation des cases de chacune des quatre strates se réalise selon un plan universel unique valable pour chaque strate distincte. Ce plan possède quatre couronnes emboîtées et 64 cases pourvues chacune de trois nombres quantiques lms.

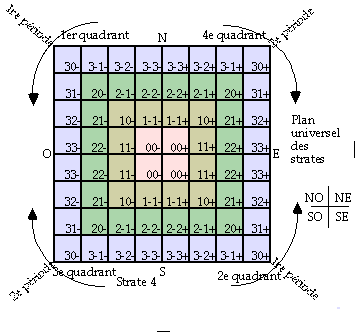
Fig.11, 67. Plan universel des strates. Il sert tout entier à la strate 4. Dans les autres strates, certaines couronnes extérieures restent inutilisées. Dans chaque case, il faut ajouter, selon la strate, les symboles de l'élément et la valeur de n quantum principal. L'occupation de chaque quadrant commence par la case voisine de l'axe nord-sud.

L'occupation de la strate procède dans l'ordre des valeurs de Z numéro atomique, la couronne la plus grande d'abord et la première période de la strate d'abord. On inscrit alors les symboles, les valeurs de Z et les valeurs de n quantum principal, dans chaque case. La valeur de n augmente d'une unité à chaque changement de couronne c'est-à-dire de l et en même temps, la valeur de l diminue d'une unité. (On vérifie ainsi la règle de Klechowski-Madelung selon laquelle la somme n+l reste constante dans une période).

La première période de la strate est inscrite au complet puis on procède à l'inscription de la deuxième période. La suite des valeurs de n rencontrées alors est la même que dans l'inscription de la première période sauf addition de l'unité. À ce moment, la figure est un carré complet sans case vide.

Chaque quadrant rempli satisfait la propriété mentionnée des carrés d'impairs : le nombre d'éléments présents est la puissance deux d'un entier, cet entier étant 1, 2, 3... , égal au nombre de cases dans le côté du quadrant

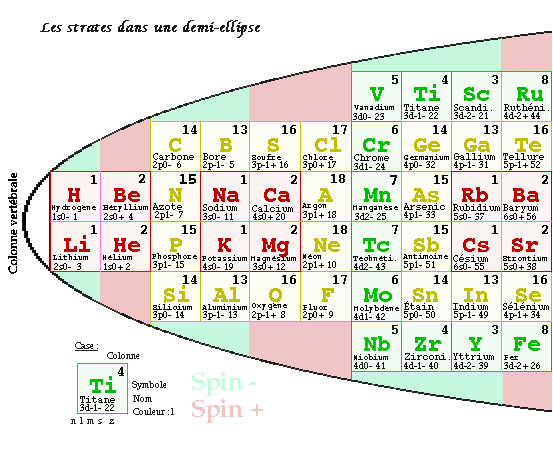
L'organisation graphique est pourvue des symétries du carré et peut s'appeler Tableau quadratique, elle s'inscrit sensiblement dans une demi-ellipse, ce qui permet de l'appeler Tableau dans une demi-ellipse. Fig. 12, 52 Pour marquer qu'il peut subir des transformations, on peut l'appeler Tableau primitif. On notera que la demi-ellipse circonscrite au Tableau a un demi grand-axe égal à un peu plus de vingt côtés de cases et un petit-axe égal à un peu plus de huit côtés de cases.

Je me permets de dire que le Tableau primitif est un succès au point de vue des symétries qu'il révêle et rend manifestes. Ce résultat découle principalement primo de l'importance accordée aux moments cinétiques l et m, tandis que le Tableau périodique des éléments s'attache surtout au nombre quantique principal et secundo, à la réflexion sur les nombres impairs et les symétries d'ordre quatre, ce qui découle de primo.

Dans ce tableau, les quatre strates sont accolées côte à côte d'ouest en est, occupant partie d'un rectangle de longueur 20 cases et hauteur 8 cases. Le tout forme un ensemble compact sans lacune ou espace vide. Un sous-ensemble de hauteur deux cases se distingue, allant de H et Li à l'ouest jusqu'à No et Yb à l'est, déterminant un rectangle de 20X2 = 40 cases et 40 éléments. Ce sont les seuls éléments dont les demi sous-couches sont complètes. Je l'appelle la Colonne vertébrale du tableau primitif.

Le Tableau primitif se trouve constitué par la juxtaposition arbitraire de quatre graphismes distincts. que rien ne m'oblige à accoler de la façon choisie. Le Tableau périodique, lui, a une logique demandant qu'on reste sur la même surface plane afin de sauter de la dernière colonne d'une période à droite à la première colonne à la période suivante à gauche et c'est là un héritage de la vis tellurique de Béguyer de Chancourtois, dessinée sur une peu commode feuille cylindrique.

Cette logique de la surface plane unique ou du moins de la surface continue où se trouverait assuré le passage en continuité d'une fin de strate au commencement de la strate suivante fait défaut dans le Tableau primitif, où les deux dimensions sont accaparées pour usage interne.

Les symétries propres au tableau des éléments ne peuvent pas se représenter complètement dans deux dimensions.

Je vois là une raison de présenter les strates en superposition, comme leur nom même, tiré du vocabulaire géologique, le suggère*. Chacune occupe deux dimensions, mais la troisième est disponible pour superposition. En remplaçant les cases planes par des cubes, on obtient des colonnes massives de continuité verticale. Il y a deux telles colonnes massives pour un numéro de colonne dans le Tableau périodique, une dans la première période de la strate et une dans la deuxième période de la strate. Au total, il y a trente-deux colonnes massives en double exemplaire (les dix-huit désignées par l'UICPA et quatorze autres pour les Lanthanides et les Actinides). Fig. 13.

*J'ai choisi le nom de strate en mémoire de Pierre-Louis Maubeuge, géologue et membre d'honneur de la LISULF (Saint-Clément 08 février 1923 - Nancy 22 janvier 1999).

Tableau elliptique. En symétrie miroir par rapport à l' axe nord-sud, les cases ds spin - à l'ouest et les cases de spin + à l'est. Le résultat est un tableau dans une ellipse. Le demi grand axe vaut un peu plus de 10 côtés de case, le demi petit-axe vaut un peu plus de 4 côtés de case Fig. 14.53

Tableau quart d'ellipse. Production d'une tétrade. Dans le Tableau elliptique, j'attribue des coordonnées algébriques x et y au centre de chaque case, le centre du système de coordonnées étant le centre de figure. Les quatre éléments ayant les mêmes coordonnées absolues |x|, |y| sont réunis dans une grande case de capacité quadruple de l'unique quadrant NO du Tableau quart d'ellipse, de coordonnées -2|x|, 2|y|. À l'intérieur de chaque grande case, les éléments reportés conservent l'orientation de leur quadrant d'origine ; dans l'ordre de valeurs de Z : NO, SE, SO, NE. Ils composent une tétrade d'éléments. Fig. 15, 54.

Une autre manière de décrire la composition d'une tétrade est celle-ci. Dans une grande case de quatre logements, on place les quatre cases du Tableau elliptique placées en X par rapport au centre de figure.

Le tableau s'inscrit sensiblement dans un quart d'ellipse ayant pour demi grand-axe un peu plus de vingt côtés de case et pour demi petit-axe un peu plus de huit côtés de case.

---

Fig. 12, 52.Tableau dans une demi-ellipse, Tableau primitif. L'un des tableaux tétraédriques. Colonnes : dix-huit désignées par l'UICPA.et quatorze autres pour les Lanthanides et les Actinides, au total, trente-deux.

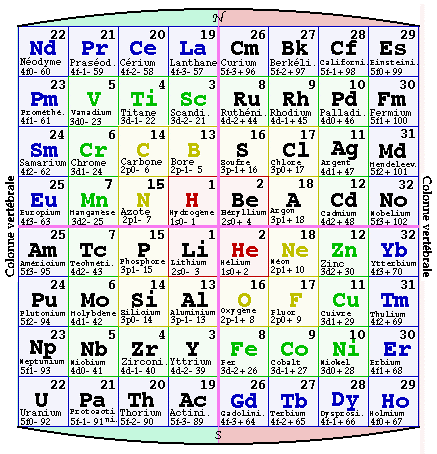
Fig. 13. Un tableau 3D. Tableau primitif tridimensionnel, les strates étant superposées. Vue en projection plane donnant la vedette aux numéros des trente-deux colonnes, chaque colonne apparaissant deux fois, une fois en couleurs dans la première période d'une strate, et une fois en noir dans la deuxième période d'une strate. La strate 1

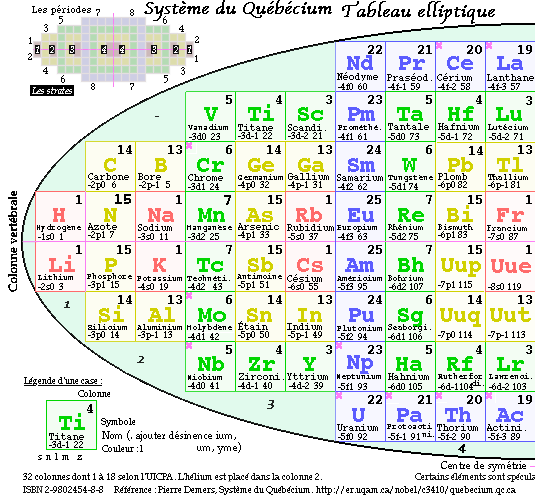
Fig. 14, 53. Tableau elliptique. http//lisulf.quebec/quebecium.qc.ca

Suite

gqajuin1.html

quebecium

Traduction interdite Tous droits de traduction réservés Suite http://www.lisulf.quebec/gqajuin2.html