DeFibonacciauQuebecium

De la science en français.

De Fibonacci au XIIIe siècle au Système du Québécium au XXIe.

Pierre Demers et collaborateurs.

Sommaire. Fibonacci en biologie et en art. Le système du Québécium : Les éléments chimiques et la géométrie. Pourquoi avons-nous 5 doigts?

Pythagore vers le siècle -5.

L’aphorisme de Pythagore: « Tout est nombre ».

Il a été perpétué aux siècles contemporains par la jolie chanson qu’on m’a apprise dans mon enfance et qui fait partie de la culture québécoise. Elle démontre à sa manière que tout est nombre.

Il n’y a qu’un seul Dieu qui règne dans les cieux,

On dit qu’il y en a 2.

Deux Testaments, l’Ancien et le Nouveau, ô…

Il n’y a qu’un seul Dieu qui règne dans les cieux,

On dit qu’il y en a 3.

Les Trois-Rivières

Deux Testaments, l’Ancien et le Nouveau, ô…

Il n’y a qu’un seul Dieu qui règne dans les cieux,

On dit qu’il y en a 4.

Catherine de Russie.

Les Trois-Rivières

Deux Testaments, l’Ancien et le Nouveau, ô…

Il n’y a qu’un seul Dieu qui règne dans les cieux,

On dit qu’il y en a 5.

Cincinnati.

Catherine de Russie.

Les Trois-Rivières

Deux Testaments, l’Ancien et le Nouveau, ô…

Il n’y a qu’un seul Dieu qui règne dans les cieux,

On dit qu’il y en a 6.

Système métrique.

Cincinnati.

Catherine de Russie.

Les Trois-Rivières

Deux Testaments, l’Ancien et le Nouveau, ô…

Il n’y a qu’un seul Dieu qui règne dans les cieux,

On dit qu’il y en a 7.

C’est épatant.

Système métrique.

Cincinnati.

Catherine de Russie.

Les Trois-Rivières.

Deux Testaments, l’Ancien et le Nouveau, ô…

Et ainsi de suite, je me rappelle, ou j’imagine le douze :

Il n’y a qu’un seul Dieu qui règne dans les cieux,

On dit qu’il y en a 12.

D’oùsque tu viens.

On se l‘arrache.

Dis-moi bonjour.

N’œuf à la coque.

Huîtres malpèques.

C’est épatant.

Système métrique.

Cincinnati.

Catherine de Russie.

Les Trois-Rivières,

Deux Testaments, l’Ancien et le Nouveau, ô…

Et je crée un 13 nouveau.

Il n’y a qu’un seul Dieu qui règne dans les cieux,

On dit qu’il y en a 13.

Et j’arrête là. Nous sommes au 13^e siècle et Fibonacci invente sa suite numérique aruthmétique aux conséquences très vastes.

Avant de parler de Fibonacci et de ses nombres, je veux rappeler qu’on a établi des catégories parmi les nombres : les entiers, les fractionnaires, les ronds, multiples de 5, les pairs divisibles exactement par 2, les impairs, les irrationnels comme le célèbre nombre pi. Les nombres premiers ne sont divisibles exactement que par 1 et par eux-mêmes. Il y a des nombres magiques, ceux ayant une importance particulière dans la compréhension de divers problèmes, comme 5 et 10 pour le système décimal de numération courant. Et parlons de Fibonacci

La suite de Fibonacci au XIIIe siècle.

Les artistes et les architectes y ont trouvé le nombre d’or qui est un nombre magique, des mathématiciens québécois en ont tiré des découvertes en biomathématique, Vieth à Montréal sur le genre Dipsacus ou Cardère, Barabé du Jardin Botanique de Montréal, Roger Jean du Collège Mérici à Québec dans un traité unique au monde Phytomathématique. http://www.puq.ca/catalogue/livres/phytomathematique-1348.html

Fig. 1. Phytomatématique par Roger Jean, 1976PUQ.

Cette suite arithmétique est simple à décrire. On écrit 1 une fois, puis une deuxième fois, cette convention arbitraire est essentielle.

1, 1,…

Ensuite on additionne 1 et 1, ce qui donne 2.

1+1 = 2.

On continue de sorte que chaque terme est la somme des deux précédents.

1+2 = 3.

2+3 = 5 etc.

Voici la suite numérique de Fibonacci.

1, 1, 3, 5, 8, 13, 21, 35, 56, 91, 147…

Elle se figure par une construction graphique spiralée. Figs 2, 3, 4.

Fig. 2. Suite de Fibonacci 2D 1 blanc, 1, 2, 3, 5, 8, 13, 21 gris, une spirale tournant dans le sens des aiguilles d’une montre.

Pourquoi cette suite de nombres plutôt qu’une autre?...

Cette suite se trouve dans les floraisons de l’ananas. Elle est présente approximativement dans les longueurs des phalanges des doigts de la main du genre homo, soit de l‘être humain. Fig. 3.

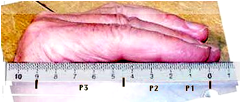
Fig. 3. Phalanges : 3e = 2^e+1^re environ.

À partir de 5, le rapport d’un terme au précédent est constamment voisin de un et deux tiers comme dans 5/3, 35/21 et tend vers une valeur limite qui est le nombre d’or 1,61803399… qui était d’avance réalisé dans les chefs-d’oeuvre antiques.

La suite du Québécium au XXIe siècle.

Fin XXe et début XXIe, j’ai découvert une autre suite numérique, qui intervient dans l’organisation de la matière inerte et de la matière vivante. Jusqu’ici, le monde scientifique l’a peu remarquée..

(Voyez http://www.lisulf.quebec/quebecium.htm

(Il est 20h HAE le samedi 16 juin 2012. À suivre.)

On écrit 1, 2, 3, 4. Pas davantage

On prend les carrés.

1, 4, 9, 16.

Remarquez que la somme est 30.

On multiplie par 4.

4, 16, 36, 64,

La somme est 120, les sommes successives sont 4, 20, 56, 120.

Dans cette courte description, 4 et 30 se distinguent parmi ces nombres et méritent de s’appeler magiques, mais c’est leur suite qui mérite surtout notre attention.

Et voilà l’essentiel de la suite du québécium.

Pourquoi du québécium?

Parce que l’idée de cette suite m’est apparue lors d’une analyse du tableau des éléments chimiques, dans lequel le dernier gaz rare serait le numéro 118, que, en l’honneur du Québec, j’ai baptisé Québécium dans une tradition d’écriture qu’on trouve dans Uranium, Hélium, Gallium, Francium et Américium etc. Le québécium 118 est un élément spéculatif, excessivement instable et jamais mis en bouteille. Pourquoi 120 plutôt que 118? C’est qu’étant rond, on peut supposer qu’il renferme davantage de régularités et de symétries. Or les symétries gouvernent le monde subatomique. Le nombre 30 est le produit des 4 premiers premiers 1, 2, 3, 5. Si on numérote les doigts de la main de 1 à 5 en commençant par le pouce, le produit de ces nombres est 120. On reconnaîtra que chacun porte le système au bout des doigts! Il n’a qu’à lever la main.

La suite du québécium peut se figurer par un jeu de carrés égaux.

Application aux atomes. Par 120 carrés égaux.

Avec disposition horizontale. Fig. 4.

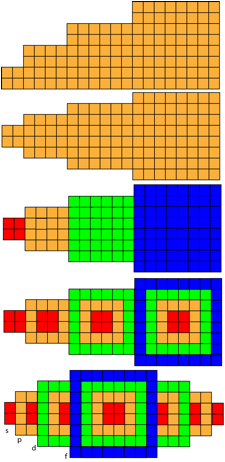
Fig. 4. Système du Québécium. Application aux atomes. Assemblages de 120 carrés égaux. Sortes d’éléments atomiques : 16 s, 18 p, 32 d, 32f, total 120. Axe horizontal. La figure du bas s’inscrit sensiblement dns une ellipse. C’est « le tableau elliptique du Québécium ».

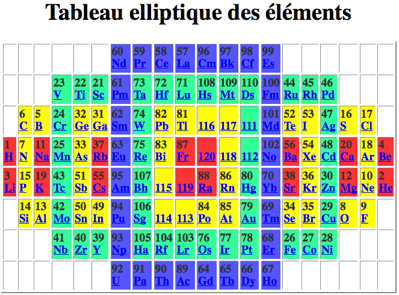
Fig. 5.Système du Québécium. Un tableau elliptique, version de Pierre Carrier, ancien doctorant de l’Université de Montréal. Les cases sont des rectangles.

Avec une disposition d’axe vertical, encore des carrés ou des rectangles. Fig. 6.

Fig. 6. Système du Québécium. Application aux atomes. Assemblages de 120 carrés égaux. Axe vertical. - Assemblage de rectangles inégaux mais tous semblables. Les 120 éléments avec leur valeurs de z nombre de charge et leurs symboles de H 1 Hydrogène à Ja 120 Janétium. Les plus abondnts occupent des cases grandes. Ceci est une nouveauté présentée pour la 1^re fois en public aujourd’hui l2 juillet 2012 à l’ÉNAP, à Québec, congrès parallèle au FMLF2012. Graphisme Maurice Day.

Une symétrie 4.

Ces figures montrent une symétrie 4, qui est encore plus apparente si l’on remplace les cases planes par des boules égales : elles s’empilent régulièrement en dessinant un tétraèdre, figure à quatre faces s’inscrivant exactement dans un cube. Fig. 7.

Fig. 7. Système du Québécium. Application aux atomes. Assemblages de 120 sphères égales s’inscrivant dans un tétraèdre, lui-même inscrit dans un cube, une arête par face du cube.1025.12-20I2010

Une application biologique : le squelette des membres humains

Examinons le squelette humain. Il se trouve que les os des 4 membres sont au nombre de 120 et que leur répartition dans chaque membre reflète la suite du Québécium ci-dessus. Le pouce vaut 1, les 4 autres doigts valent 4 etc.. Fig. 7.

Figs 7. Système du Québécium. Parallèle atomes et squelette, nombre magique120 et symétrie 4. Photo et graphismes Maurice Day. ACFAS en 2008 à Québec. http://www.er.uqam.ca/nobel/c3410/ACFAS2008QbPlaEvoAtXI2007.htm

Si nous avons 5 doigts, voilà au moins un commencement d’explication: c’est parce qu’il existe une suite arithmétique qu’il faut respecter. Si Pythagore revenait, il se réjouirait et dirait : « Vous voyez bien, j’avais raison! »

Il existe une autre application biologique, celle-là au code génétique. 1^er juillet 2012, 20h09HE

Merci à Pierre Carrier, Hélène Trudeau, Maurice Day et Parick demers pour leurs contributions.

Références.

Réf.1. Contribution de Hélène Trudeau 2012. 24VI2012

Bonsoir, âme solitaire,

Distraite par une longue conversation téléphonique avec une amie, j’ai omis, comme j’en avais l’intention, de vous envoyer un courriel pour vous souhaiter Bonne Saint-Jean. Vous demeurez occupé et intéressé par tous les aspects de l’actualité : signe de santé physique et mentale. Bien entendu, à nos âges, l’énergie n’est pas toujours au rendez-vous. Bonne Saint-Jean tout de même.

1° Voici l’adresse où vous trouverez les paroles de votre chanson, mais je ne reconnais pas les couplets. Cela me semble une adaptation de 2002 pr les Charbonniers de l’enfer.

http://www.acpo.on.ca/claude/charbon/chanson/seuldieu.htm

2° Ici, des traces des paroles que vous m’avez citées :

Les deux testaments

Une autre chanson à saveur biblique a alors monté à mes lèvres et qui donnait comme refrain : il n'y a qu'un seul Dieu qui règne dans les cieux… Et la chanson continuait : On dit qu'il y en a deux, deux testaments, l'Ancien et le Nouveau ho, ho, ho, ho… Je ne connaissais alors que les testaments des dernières volontés des vieilles gens… Quand même! C'est vous dire combien mes connaissances bibliques étaient pauvres. Cependant, à ma défense,  je n'avais que sept ou huit ans, la bible n'était pas encore sur les rayons de notre maigre bibliothèque familiale. Et à l'école, c'était « L'histoire sainte » qui en tenait lieu.

La tête remplie de refrains pieux, je suis allée chercher les albums de chants qui ont nourri mon enfance et je les ai feuilletés avec un brin de nostalgie. Je me suis rendue compte que tout était bien gravé dans la mémoire du cœur et que je pouvais chanter plusieurs de ces chansons presque sans fausses notes… Je me permets d'en tourner les pages avec vous.

Ghislaine Salvail s.j.s.h.  -  03 février 2012            relevé sur http://catechese-ressources.com/bible-et-culture-populaire

…………………………

3° Maintenant, nous y sommes.

UN SEUL DIEU

lundi 16 juillet 2007 :: Chansons scoutes (Des)

I
Il n'y a qu'un seul Dieu 
Qui règne dans les cieux.

II
On dit qu'il y en a deux: 
Deux Testaments 
L'ancien et le nouveau oh! oh! ... 
Il n'y a qu'un seul Dieu 
Qui règne dans les cieux.

III
On dit qu'il y en a trois :
Les Trois-Rivières
Deux testaments: 
L'ancien et le nouveau oh! oh! ... 
Il n'y a qu'un seul Dieu 
Qui règne dans les cieux.

IV
On dit qu'il y en a quatre: 
Catherine de Russie
Les Trois-Rivières
Deux testaments:... (etc…)

V
On dit qu'il y en a cinq: 
Cincinnati
Catherine de Russie
Les Trois-Rivières... (etc…)

VI
On dit qu'il y en a six: 
Système métrique
Cincinnati
Catherine de Russie... (etc…)

VII
On dit qu'il y en a sept: 
C'est épatant
Système métrique
Cincinnati... (etc…)

VIII
On dit qu'il y en a huit : Huître Malpèque (etc…)

IX
On dit qu'il y en a neuf: N’œuf à la coque (etc…)

X
On dit qu'il y en a dix: Disputez-vous (etc…)

XI
On dit qu'il y en a onze: On s'désennuie (etc…)

XII
On dit qu'il y en a douze: D'où c'que tu d'viens ? (etc…)

XIII
On dit qu'il y en a treize: Très embêtant (etc…)

XIV
On dit qu'il y en a quatorze: Quatorze de juillet (etc…)

XV
On dit qu'il y en a quinze: Quins z’y les pieds (etc…)

XVI
On dit qu'il y en a seize: 
Cess’ de chialer
Quins z’y les pieds
Quatorze de juillet
Très embêtant
D'où c'que tu d'viens ?
On s'désennuie
Disputez-vous
N’œuf à la coque
Huître Malpèque
C'est épatant
Système métrique
Cincinnati... 
Catherine de Russie
Les Trois-Rivières
Deux testaments
L'ancien et le nouveau oh! oh! ... 
Il n'y a qu'un seul Dieu 
Qui règne dans les cieux.

Tiré de «Le scout rit et chante dans ses difficultés»,

Accessible à                http://www.mlebelm.ca/index.php?Chansons-scoutes-des/p5

Saviez-vous que l’йnumйration se rendait jusqu’а seize ? Reconnaissez-vous la chanson que vous cherchiez ? Je l’espиre.

Bonne nuit.

Hélène Trudeau

Candiac

- • -