DesEtats5bis;
http://www.lisulf.quebec/
Des tats
de l'hydrogne aux lments du
tableau.
Pierre
Demers
Traduction
interdite 7III2009
Sommaire.
Je me donne une grille
vide et un tableau des tats de l'atome
d'hydrogne avec les blocs d'lments
correspondants, en application des principes de
Pauli et de Zeeman. Je montre que le peuplement de
strates 1, 2, 3, 4 dcoule naturellement de ces 2
donnes par l'application de rgles de symtrie
simples. Le rsultat est 4 strates qui, accoles
donnent le tableau en demi-ellipse des lments.
Divis selon les spins, ce tableau donne le
tableau elliptique des lments. Chaque strate et
le tableau final dmontrent une symtrie 4
quivalente 2 symtries miroirs
croises.
Grilles
donnes.
Je me
donne une grille carre avec un centre et des
cases carres, oriente NSEO, 8 cases de
ct.
Elle a 4 quadrants. La moiti ouest est
rserve aux spins -, la moiti est, aux spins +.
Une case loge un lment. Le quadrant NO est
compos des 4 impairs les plus petits 1, 3, 5, 7,
qui sont des 1ers.
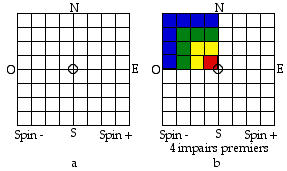
Fig. 1. a. Grille. b. Les impairs
1, 3, 5, 7 sont colors RJVB dans le quadrant NO,
image des 3 autres.
Ce cadre n'est pas
neutre, l'exemple de tout autre cadre de
classification. Le cadre du populaire tableau de
Mendeleev n'est pas neutre. Il impose des ranges
de priodes et des colonnes de groupes, en plus
d'une rallonge de 2 ranges. Le prsent cadre est
cod, il comporte certaines exigences d'criture
ou rgles d'usage, entre autres des symtries
planes angles droits. Voyons ce que nous pouvons
tirer de son usage.

Fig. 1bis.
Affectations des cases, emplacement de la case
initiale, 1re case occupe lors du remplissage
d'une strate. Affectations.gif
Rgles
d'usage de la grille.
J'essaie d'utiliser
cette grille de la faon la plus symtrique
possible, et de formuler cet effet des rgles
rgissant son usage lors de son remplissage par
les blocs d'lments. Fig. 1bis.
01. Un
bloc s'crit en commenant par la case initiale.
Un 1er demi-bloc est inscrit, puis l'criture se
poursuit dans le quadrant oppos. De la sorte, les
1ers lments inscrits acquirent le spin -, les
derniers, le spin +. Point n'est besoin que le
signe du spin des demi-blocs soit spcifi
d'avance : cette spcification s'effectue
automatiquement par suite du code li la grille.
02. Une querre se loge exclusivement dans un
espace de la grille qui lui est exactement adapt.
(Il y a 4 sortes d'querres et d'espaces
adapts.)
03. Une strate
complte n'a aucune case vide.
04. On
exploite les ressources en blocs disponibles selon
2 critres dans lÕordre.
a
nergtique, de la plus basse nergie
possible dans le Tableau 1.
b gomtrique, qui
convienne aux espaces disponibles dans la grille.
(gomtrique est prdominant.)
05. On commence le
peuplement d'une grille vide successivement par un
bloc s, puis p, puis d, puis f. Il y aura donc 4
strates.
06. Une
fois la la couronne initiale dfinie, le
peuplement ne peut pas se poursuivre l'extrieur
de cette couronne.
La suite dmontre
que ces rgles sont applicables et conduisent
des tableaux cohrents de symtries 4. Les rgles
de Madelung, de Klechkowski et de Hund n'ont pas
d'application.
Donnes
sur l'hydrogne, consensus sur les
blocs.
Je rfre au
traditionnel diagramme de Balmer.
http://www.chimix.com/devoirs/t195.htm donne
un diagramme simplifi des tats. J'ai ajout une
chelle des nergies d'excitation et une autre des
valeurs de n.
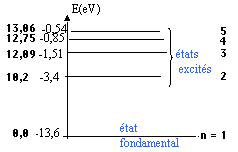
Fig. 2.
Diagramme simplifi de Balmer, d'aprs
chimix.
J'ai
transcrit jusqu' la ligne 8s la liste ordonne
des tats excits de l'atome d'hydrogne,
Appendice 1, Tableau 1 est un abrg, ne retenant
que les lignes fonctionnelles. nergie 0 dans
l'tat fondamental. Ë un tat choisi de l'atome
d'hydrogne correspond un certain nombre de
valeurs de z
formant un bloc : 2, 6, 10, 14, selon les
conditions quantiques, entre autres selon la rgle
de Hund : un nombre impair d'lments de spin -,
puis un nombre gal de spin +. Le nombre impair
est 1, 3, 5 ou 7. Tableau 1. Le niveau d'nergie E
de l'tat augmente de haut en bas. Pour certains
tats, 2 valeurs de l'nergie apparaissent, Min et
Max
http://physics.nist.gov/cgi-bin/ASD/energy1.pl
Tableau
1
tats H et lments
z
les
correspondances
tats de
l'atome d'hydrpgne.....Valeurs de z en
..Description.....E(eV)....................correspondance.
Soulign : spin -....Par
nergie
Ligne.Terme.........................Bloc s
Bloc p.....Bloc
d.......Bloc
f....Strate......Max Min
......nl...........j...........................................................Les
20 blocs..1....2......3.....4
1...1s..2S..1/2 ...0,0
...............1\2.................................<1..........S1......................1....1
2...2p.2P¡.1/2..10,1988057...5,
6, 7\8, 9,
10.....................<3.........S2.................3....2
3...............3/2 .10,1988511
4...2s..2S..1/2 .10,1988101... 3\4...................................2>.........S1....................2....3
5...3p 2P¡.1/2 12,0874931...13,
14, 15\16, 17, 18..............5...........S2...........4,.5....4
6................3/2.12,0875066
7...3s...2S..1/2.12,0874944...11\12.....................................4...........S2...........4, 5....5
8...3d..2D
.3/2.12,0875065...21, 22, 23, 24,
25\26, 27, 28, 29, 30..<7....S3.....6......6
9................5/2 12,0875110
10.4p..2P¡1/2..12,7485319...31, 32,
33\34, 35, 36...........................8......S3.....8.....7
11.............3/2..12,7485375
12.4s...2S..1/2.12,7485324 ..19\20.......................................6>........S2.............7.....5
13.4d..2D
3/2 12,7485375 39, 40, 41, 42, 43\44,
45, 46, 47, 48 ..10.....S3....9.....9
14.............5/2..12,7485394
15.4f...2F¡.5/2.12,7485394
57,
58, 59, 60, 61, 62, 63\64, 65, 66, 67, 68, 69,
70
16..............7/2.12,7485404
................................................................<13....S4..10.10
17.5p..2P¡.1/2.13,0544976 49, 50, 51\52, 53,
54............................11....S3.......12.11
18..............3/2.13,0545005
19.5s...2S..1/2 13,0544979
..37\38.....................................................9.....S3......11.12
20.5d.2D..3/2 .13,0545005
71,
72, 73, 74, 75\76, 77, 78, 79,
80........14.....S4.13.13
21.............5/2..13,0545015
22.5f,,2F¡.5/2 13,0545015 89, 90, 91, 92, 93, 94,
95\96, 97, 98, 99, 100, 102,
102
23..............7/2
13,0545019 ...................................................................17....S4..14.14
26.6p
2P¡1/2
13,2207009 81, 82, 83\84,
85, 86................................15.....S4.16.15
27.............3/2
13,2207025
28 6s 2S .1/2
13.2207010....55\56....................................................12>....S3...15.16
29 6d 2D 3/2 13,2207025
103, 104, 105, 106,
107\108, 109, 110, 111, 112.
30..............5/2
13,2207031 ..................................................................18....S4.17.17
37.7p..2P¡1/2 .13,3209160
.113, 114, 115\116, 117,
Qb......................19....S4.18.18
39.7s 2S
..1/2
13.3209161...87\88........................................................16....S4.19.19
52.8s.2S....1/2
.13,3859595
119\120....................................................20>..S4.20.20
Critres nergtiques. Min. La colonne
l'extrme droite donne l'ordre d'apparition du
bloc dans le tableau des lments, s'il ne
dpendait que de l'nergie Min. Max La colonne qui
prcde donne l'ordre d'apparition du bloc dans le
tableau des lments, s'il ne dpendait que de
l'nergie Max. Ces ordres d'apparition ne
s'accordent que grossirement avec l'ordre
exprimental.
Conditionsquantiques.
tats s. Ë cause du principe de Pauli, les
tats s de l'hydrogne sont doubls, spin -
d'abord..
tats p,
d, f. Ë cause de la leve de dgnrescence lie
au quantum magntique m ayant 2l+1 valeurs, et de
l'application du principe de Pauli, les tats de
l'hydrogne sont multiplis ainsi : tats p,
facteur 6; tats d, facteur 10; tats f, facteur
14. Les lments de spin - forment
le 1er sous-bloc : 3, 5, 7. Je traite tous les
lments comme s'ils taient rguliers.
Blocs et
querres.
Dans leur
figuration dans la grille, il y a 4 sortes de
blocs, chaque bloc tant form de 2 querres
gales symtriques Une querre a 2 bras gaux, Les
bras de l'querre s sont nuls. Fig. 3. Les
querres peuvent se tourner d'un nombre entier de
fois un droit dans leur plan. On peut choisir de
les peupler partir d'une extrmit ou de
l'autre.
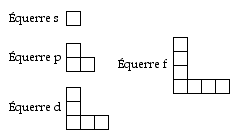
Fig. 3. querres.
Une
querre est adapte l'un de 4 placements dans la
grille, ces placements formant une couronne
carre. Fig. 4.
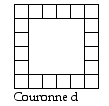
Fig. 4. La couronne carre des 4
placements d'une querre (ici, l'querre
d).
Exploitation
des blocs.
L'exploitation des blocs disponibles est
dcrite en dtail ci-aprs. Pour chaque strate,
on choisit de la commencer par le bloc
nergtiquement le plus conomique d'accs parmi
ceux qui ne sont pas encore employs. Ce bloc est
mis en vidence au Tableau 1 : S1, S2, S3, S4.
Strate
1.
Je place
l'querre 1 dans le quadrant NO, le plus
prs possible de l'origine. Par symtrie,
l'querre 2 doit se placer dans la case +
diamtralement oppose. Ainsi se trouve amorc le
peuplement d'une strate. L'espace peupler est
dfini par la 1re querre implante. Un peu comme
un graphiste qui, en plaant un point sur une
feuille, en dtermine 3 autres par imagerie miroir
et par suite un rectangle occuper. (La mthode
vectorielle?)
Ici
l'espace occuper est celui des 4 cases
centrales. Une autre manire d'exprimer la
contrainte impose est une recherche de symtrie.
Pour satisfaire la symtrie encore, il manque
remplir 2 cases afin de complter une figure
carre : 3 et 4 sont disponibles. Ainsi se
trouve complte la strate 1 en 2 priodes de 2
lments.
Une fois
une strate amorce, elle doit tre complte avant
qu'on ne procde amorcer et peupler une
autre.
Si le
remplissage obissait uniqement au critre
nergtique Min, aprs le 2e lment, l'lment
suivant dans le tableau des lments serait l'un
d'un bloc p, contrairement l'exprience. Le
critre gomtrique propos ici donne la suite
correcte : c'est un lment s.
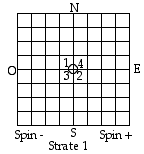
Fig. 5. Strate 1
complte.
Strate
2.
La strate
1 est
mise de ct et il faut poursuivre amorcer une
strate 2. Il faut un retour en arrire dans le
Tableau 1, puisqu'on a pass par dessus la ligne 2.
De la ligne 2, je saisis l'querre 5, 6, 7,
que je place dans le quadrant NO, le plus prs
possible de l'origine, l'ouverture vers l'origine.
Aussi bien que pour la strate 1, je placerai
l'querre 8, 9, 10 en symtrie miroir par rapport
l'origine dans le quadrant SE. Il apparat 2
carrs incomplets. Il me faut les complter en
recourant aux querres s 11 et 12. de la
ligne 7.

Fig. 6. Vers strate 2.
Je me
sers de la ligne 5. Je place l'querre 13, 14,
15 dans le quadrant SO, l'querre 16, 17, 18
dans le quadrant NE, puis les querres 19
et 20 de la ligne 12 et la strate 2 est complte.
Fig7
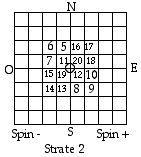
Fig. 7. Strate 2
complte.
Strate
3.
La strate
2 est mise de ct et seuls les blocs S3, S4 subsistent
dans le Tableau 1. Je prends le 1er qui se
prsente, qui est S3.
De ligne 8 j'inscris les 5 lments -d que sont
39, 40, 41, 42, 43 dans le
quadrant NO, puis les 5 lments d+ en opposition
dans le quadrant SE.. Il faut complter le contenu
de ces quadrants par les lments p et s des
lignes 10 et 19 respectivement. Ainsi sont saturs
les quadrants NO et SE de la strate 3. Fig.
8.

Fig. 8. Vers strate 3.
Je
poursuis. J'inscris les 5 lments -d ligne 13 que
sont 39 43 dans le quadrant SO, puis les 5
lments d en opposition dans le quadrant NE.. Il
fauf complter le contenu de ces quadrants par les
lments p et s des lignes 17 et 28
respectivement. Ainsi sont saturs les quadrants
SO et NE de la strate 3.

Fig. 9. Strate 3
complte.
Strate
4.
La strate
3 est
mise de ct et seul les 8 blocs S4 subsistent
dans le Tableau 1, avec ses 8 lignes. Je laisse au
lecteur le soin de procder. Aux valeurs
numriques prs, le processus rpte celui de la
strate 3, sauf qu'il est prcd dans chaque
quadrant par l'installation d'une querre f, 4 au
total, formant une couronne de 28 cases. Fig
10.
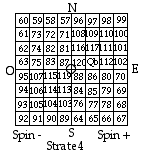
Fig. 10. Strate 4
complte.
Superflues.
Dans
l'argumentation ci-dessus, il apparat superflu
d'invoquer les rgles de Madelung, de Klechkowski,
de Hund et les quations des orbitales.
J'introduis des contraintes gomtriques, qui sont
des sortes de rgles de slection et
d'interdiction. Je remercie certains Sceptiques
pour des critiques constructives, entre autres
Bernard Schaeffer et curieux. "La
classification des lments est simplement fonde
sur la gomtrie." Elle est
platonicienne.
Les 4
strates.
Les 4
strates compltes ci-dessus peuvent s'assembler
jointivement dans l'ordre 1, 2, 3, 4 pour donner
un tableau de contour semi-elliptique, le
grand-axe de l'ellipse tant vertical ou
horizontal. Figs 11, 12.
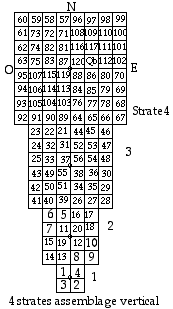
Fig. 11.
Assemblage vertical.

Fig. 12. Assemblage
horizonal.
Tableau
semi-elliptique des lments.
L'assemblage horizontal de la figure 12
est quivalent au tableau semi-elliptique des
lments. Fig. 12.
http://www.lisulf.quebec/QbS2Fig365a.gif
http://www.lisulf.quebec/QbS2Fig365b.gif
XXXX
Fig. 12.
Tableau semi-elliptique des lments
Tableau
elliptique des lments.
Par des
dplacements vers l'est des cases de spin + des
strates 1, 2, 3, on obtient le tableau elliptique
des lments. Fig. 13.
http://www.er.uqam.ca/nobel/c3410/TableauelliptiqueC.gif
XXXX
Fig. 13.
Tableau elliptique des lments
Symtrie
4 des strates et du Tableau elliptique des
lments.
La
symtrie 4 est une partie inalinable de la nature
des atomes. Elle se manifeste dans chaque strate
et dans le tableau elliptique par 2 pliages la
manire d'un mouchoir. La symtrie 4 appele de
pliage mouchoir peut encore se dcrire par 2
symtries miroirs, les miroirs plans requis sont
supposs croiss et forment un tridre avec le
plan de la grille, ayant pour origine le centre de
celle-ci. Fig. 14.
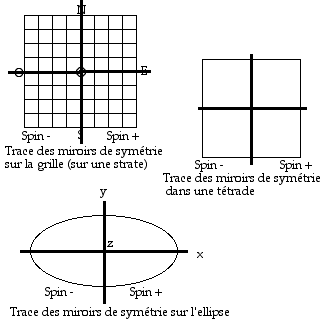
Fig. 14. Traces des miroirs de
symtrie.
Chaque
lment appartient un groupe de 4 appel
ttrade. La structure de chaque ttrade rpond au
schma Fig 15. Dans les 4 cases, les
valeurs de l et de m sont les mmes, on y trouve n
et n+1, les spins - et +. Il y a 30 ttrades selon
les couples permis (l, m). La symtrie
4 se manifeste aussi dans chaque ttrade.

Fg. 15.
Symtrie 4 des atomes. Dans une ttrade, les
valeurs de l et de m sont les mmes dans les 4
cases. Exemple de 2 ttrades : ttrade H, ttrade
Ti. Rh est irrgulier, on l'a trait comme s'il
tait rgulier. Voyez les 30 ttrades dans le
tableau quart d'ellipse.
http://www.lisulf.quebec/Quartd12,5cm.gif
Miroirs
verseurs. Axe de
symtrie.
Dans la
figure 14, un effet du miroir de trace NS est
d'inverser le signe du spin. En bref : un miroir
NS est un verseur du spin.
De plus :
un miroir (NS ou OE) change n d'une unit, soit en
plus, soit en moins. Deux miroirs croiss
conservent la valeur de n; ils sont l'quivalent
d'un axe de symtrie z passant par leur rencontre.
En d'autres termes, la valeur de n se conserve
dans une symtrie par rapport au centre de
figure.
Les 4
strates platoniciennes 3D.
Dans
cette section, je remplace les cases par des
boules.
¥Strate
1. Quatre boules. Or 4 boules peuvent
s'assembler, l'une tant porte par les 3 autres,
pour dessiner un ttradre rgulier, solide de
Platon
¥Strate
2. Seize boules. Or 16 boules peuvent s'assembler
en 2 niveaux, chacune de l'tage suprieur
reposant sur 3 de l'tage infrieur pour dessiner
un tronc de ttradre rgulier, portion d'un
solide de Platon. L'tage infrieur a 4 boules de
ct.
¥Strate
3. Trente-six boules. Or 36 boules
peuvent s'assembler, chacune de l'tage suprieur
reposant sur 3 de l'tage infrieur pour dessiner
un tronc de ttradre rgulier, portion d'un
solide de Platon. L'tage infrieur a 6 boules de
ct.
¥Strate
4. Soixante-quatre boules. Or 64 boules peuvent
s'assembler, chacune de l'tage suprieur reposant
sur 3 de l'tage infrieur pour dessiner un tronc
de ttradre rgulier. L'tage infrieur a 8
boules de ct.
¥¥Les 4
strates. Cent vingt boules. Or les 4 figures 3D
obtenues peuvent se superposer pour former une
figure comprenant 120 boules, ayant 8 boules de
ct et dessinant un ttradre
rgulier.
Confection
du tableau par criture des valeurs de
n.
Je
commence par figurer les grilles de 4 strates N* =
1, 2, 3, 4 vides mais codes en slm, en omettant
les cases qui resteront vides. Fig. C1. (Ë
suivre)
http://www.lisulf.quebec/Cconfectab.htm
-30-














