EquerreJanetScerri

Système du Québécium.

Mise en équerres du tableau de Janet-Scerri des éléments chimiques.

Pierre Demers

26II-8III2010

Traduction interdite.

Termes de référence :

Résumé. Éric Scerri a recommandé un tableau périodique 2D des éléments chimiques z=1 à 120 en récrivant sur 7 lignes celui de Janet. Je montre que ce tableau, par des manipulations géométriques, donne facilement naissance à 40 équerres équilatérales, qui s’assemblent naturellement en 4 strates carrées. Ces strates, divisées selon les spins – et +, donnent le tableau elliptique du québécium 2D. - On remplace dans les strates les cases carrées par des sphères, on les réorganise par des glissements pour obtenir des strates losanges, puis par des retournements, des empilements 3D en forme de troncs de tétraèdres ayant 2 niveaux par strate. Les 4 troncs obtenus se superposent pour s’inscrire dans un tétraèdre régulier 3D ayant 8 sphères de côté et 8 niveaux. – Si on remplace les cases carrées par des triangles équilatéraux, on aboutit à 4 surfaces triangulaires occupées par les cases, inscrites dans un tétraèdre régulier. – On voit une fois de plus que la géométrie quantique offre une explication globale de l’organisation du tableau, inexpliquée jusqu’à maintenant au-delà de la période 2 traditionnelle. Réf. 1, 2.

Le tableau Janet-Scerri et ses transformations.

Le tableau Janet-Scerri se trouve à la figure 3 réfèrence 1. Il comporte 7 lignes, la 1^re contenant la 1^re et la 2^e ligne de celui de Janet. Je le récris avec les couleurs RJVB pour les éléments spdf, et des additions le complétant jusqu’à z = 120.

Les figures 1 à 4 montrent le tableau de Janet-Scerri, puis sa réécriture en cubes au lieu de cases. L’usage de ces cubes a été décrit Réf. 3. Ces cubes sont ensuite formés en équerres symétriques.

Fig. 1. Le tableau Janet-Scerri. Les lignes 1 et 2 du tableau de Janet sont ici réunies en une seule. Réf. 1. Ces 2 lignes sont montrées distinctes dans l’encart.

Fig. 2. . Le tableau Janet-Scerri en cubes, dont les parois sont vert pâle ou rose pour les spins - ou +. Le code est RJVB pour spdf. L’assemblage est divisé en 16 blocs d’un cube, 12 de 3, 8 de 5, 4 de 7, un bloc par demi sous-couche. Remarquez les impairs.

Fig. 3. Seize équerres symétriques formées d’un cube-élément, 12 de 3. Les équerres d’un cube n’ont pas de bras.

Fig. 4. Huit équerres symétriques formées de 5 cubes-éléments, 4 de 7.

Ces 40 équerres peuvent s’assembler de multiples façons. Celles de même période peuvent ainsi donner 8 assemblages compacts rectangulaires, renfermant chacun 2 quadrants égaux. De la sorte, apparaît une sorte de symétrie générale à tout le tableau des éléments. Fig. 5. Ces rectangles forment 4 paires que j’ai appelées des strates. Je préfère la disposition selon la figure 6 en strates carrées, les quadrants d’une période étant de symétrique par rapport aucentre du carré La structure de la strate 4 se répète dans les autres avec des suppressions.

Fig. 5. Assemblages des cubes en 8 rectangles, un par période. Les rectangles forment 4 paires semblables 2 à 2. Ils sont composés chacun de 2 quadrants carrés.

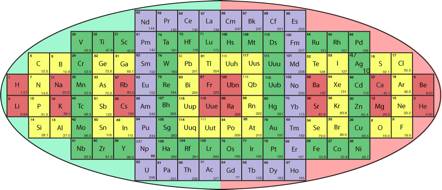
Fig 6. Système du québécium. Tableau semi-elliptique. Seize quadrants en 4 strates. Les spins -+ alternent de l‘ouest versl’est. On peut empiler les strates On voit dans chaque case, en haut à droite, le numéro de la colonne traditionnelle. Ce numéro est répété 2 fois dans l’empilement.

Les 4 strates s’inscrivent sensiblement dans une demi-ellipse. Répondant au programme idéal de Nemmi Noëther de recherche de symétries fondamentales, le tableau semi-elliptique présente une symétrie de structure concentrique autour du centre de figure de chaque strate. On peut atteindre une symétrie de structure autour du centre de figure.de l’ensemble du tableau en déplaçant 6 quadrants vers l’est. La figure est un double miroir, les miroirs sont l’axe nord-sud et l’axe ouest-est. C’est le tableau elliptique des éléments Fig. 7.

Dans ce tableau, les 4 éléments placés symétriquement selon des X ont les mêmes valeurs de l et m, ils diffèrent par les valeurs de n et s.

Fig. 7. Système du québécium. Tableau elliptique. Seize quadrants en 8 demi-strates, spins -+ ouest est.Tableau elliptique.

Tableau 1, relatif au tableau elliptique Fig. 7.

valeurs l et m dans les cases du quadrant NO

Strate 1.....2................3...............................4

Rangée du haut

...............................................................f0, f-1, f-2, .f-3 ;

..................................d0, d-1, d-2, f1, d0, d-1, d-2 ;

...............p0, p-1, d1, p0, p-1, f2, d1, p0, p-1 ;

s0, p1, s0, d2, p1, s0, f3, d2, p1, s0.

Rangée du bas

Ces valeurs se répètent avec symétries miroirs dans les 3 autres quadrants

Les éléments répétés par symétries miroirs forment une tétrade. En groupant les éléments par tétrades, on obtient un tableau quart d’ellipse de 30 tétrades. Fig. 8

Fig. 8. Système du québécium. Tableau en quart d’ellipse de 30 tétrades. Dans une tétrade on inscrit les 4 éléments d’une strate ayant les mêmes valeurs de l et de m.

À l’intérieur d’une tétrade, les 4 éléments ont les mêmes valeurs de l et de m, , ils diffèrent par les valeurs de n et s. Voici les valeurs de l et m dans les 30 tétrades en commençant par la rangée supérieure. Tableau 1.

Tableau 2, relatif au tableau en quart d’ellipse Fig. 8.

valeurs l et m dans les tétrades

Strate 1.....2................3...............................4

Rangée du haut

...............................................................f0, f-1, f-2, .f-3 ;

..................................d0, d-1, d-2, f1, d0, d-1, d-2 ;

...............p0, p-1, d1, p0, p-1, f2, d1, p0, p-1 ;

s0, p1, s0, d2, p1, s0, f3, d2, p1, s0

Rangée du bas

Passage à 3D.

Dans le tableau semi-elliptique, je remplace les cases en carrés ou en cubes par des boules s’y logeant. Dans chaque strate elles forment en arrangement carré ayant n boules de côté et comptant n2 boules = 4, 16, 36 ou 64, et je les contrains à prendre un arrangement losange. Cet arrangement possède, à sa plus grande largeur, une suite rectiligne de n boules. Autour de cette suite, je fais pivoter vers le haut l‘ensemble des [n(n-1)]/2 boules situées d’un côté, et elles viennent s’appliquer au dessus des autres, établissant une structure de 2 étages. Fig. 9. Cette structure 3D s’inscrit dans un tronc de tétraèdre régulier. Les 4 structures superposées avec leurs 8 niveaux s’inscrivent dans un tétraèdre régulier. Fig. 10.

Fig. 9. Exemple de passage à 3D. Les 16 casesde la strate 2 sont devenues 16 boules en arrangement carré. Par contrainte, elles s‘arrangent en losange. Par pivotement, 6 boules se placent au dessus des 10 autres. Il résulte un empilement en tronc de tétraèdre.

Fig. 10.Tableau en tétraèdre de boules. Il s’incrit dans un cube, une arète par face du cube. La strate 4 avec ses 64 boules commence dans les deux niveaux de boules B et s’étend vers le bas de la figure. J’ai réalisé ce tableau fin 1998. Réf. 4.

Fig. 11. Tableau en 4 feuilles triangulaires portant les cases triangles des éléments, inscrites dans un tétraèdre régulier. Les éléments sont figurés par des triangles en tête-bèche. La strate 4 est à gauche. Mars 2010.

Réf. 14

La géométrie du tétraèdre régulier lui permet de loger exactement des carrés, des rectangles et plus généralement, des trapèzes, s’appuyant sur 2 faces dièdres, ayant une arête commune, comme je l’ai décrit dans ma publication Réf. 14. Grâce à ce principe, Tsimmermann a pu représenter la totalité des 120 éléments par des cartes rectangulaires logées dans un tétraèdre ; chaque carte portant des cases rectangulaires portant le nom d’un élément. Une carte pour chaque valeur de l, il y 4 cartes : spdf. En modifiant sa présentation, je présente les 4 strates sous l’aspect d’un empilement de cartes carrées logées dans un dièdre d’un tétraèdre. Fig. 12.

Fig. 12. À l’intérieur d’un tétraèdre régulier, les 4 strates sont représentées chacune par une carte carrée assises sur 2 faces dièdres. L’arête dièdre est en haut. Mars 2010.

Pourquoi l’existence des strates?

Dans le langage du système traditionnel, pourquoi les périodes 3, 4, 5, 6 et 7 ont-elles respectivement 8, 16, 16, 32 et 32 termes, alors que, conformément à une certaine extension du modèle de Bohr de l’atome H, la prévision est qu’elles devraient en avoir 18, 32, 50, 72 et 96? Cette prévision erronée est très loin de la réalité, et c’est peut-être pour cette raison qu’elle est rarement exposée dans la littérature; elle discrédite en quelque sorte le modèle de Bohr lorsqu’on essaie de l’appliquer aux atomes autres que H. Et encore, pourquoi, lorsqu’on observe le tableau de Mendeleev traditionnel solidement implanté partout, peut-on observer que les périodes se présentent en paires de mêmes longueurs après la 1^re , soit 8 et 8, 18 et 18, 32 et 32?

1. J’ai d’abord formalisé l’affirmation empirique et j’en ai fait une règle, quitte à la justifier plus tard, et c’est mon 1^er postulat:

«les périodes se présentent par paires d’égales longueurs », que j’appelle strates.

2. Et voici mon 2^e postulat :

« la suite de éléments finit sur un gaz rare que j’ai appelé québécium, de numéro z = 118. »

3. Il me fallait ajouter une remarque ou un 3^e postulat :

« pour des raisons inconnues, la règle ne s’applique pas à la 1^re strate, qui ne contient qu’une période, de 2 éléments, H et He. »

De la sorte, il y a 4 strates.

Je tiens pour importante la notion généralisée de strate pour assurer telle symétrie d’ensemble d’ordre 4 du tableau, afin qu’on puisse le considérer comme formé de 4 parties similaires. Il serait dificilement concevable que les 2 premiers éléments échappent à une règle aussi évidemment vérifiée dans les nombreux éléments qui les suivent. C’était ma conclusion en 1997. Réf. 5.

Il fallait donc impérativement corriger cette erreur de la nature, me disais-je. Un peu plus, j’aurais proclamé : « Symétrie d’abord, expérience ensuite » ! Il faut 2 périodes et 4 éléments dans la strate 1

J’ai tenté de placer les 2 éléments spéculatifs 119 et 120 dans une période virtuelle précédant celle contenant H et He. Cette tentative pouvant se justifier par une hypothétique nouvelle règle de symétrie, qui affirmerait que la disposition des éléments constituerait un cycle fermé sur lui même au nombre 120. Mais cette nouvelle règle paraît extravagante, car, pourquoi imposer l’idée ad hoc d’un cycle fermé

Et je je me trouvais confronté à une prévention que je voulais respecter, je voulais respecter une tradition qui me paraissait intouchable, remontant à Mendeleev lui-même savoir que 1^re période soit obligatoirement confinée à 2 éléments, et suivie d’une 2^e période de 8 éléments et non de 2. La tradition exigeant en outre que toute période commence par un alcalin et se termine sur un gaz rare.

J’ai commensé à penser qu’il n’y avait pas une erreur de la nature, mais une erreur humaine. Une erreur humaine ou disons plutôt un mauvais choix dans la représenttion du commencement du tableau.

J’ai connu le tableau de Charles Janet par le livre de Van Spronsen, qui le présente sans le recommander. Ce tableau créé une 2^e ligne contenant les 2 éléments Li et Be enlevés à la 2^e période traditionnelle, et qui termine ses lignes sur un élément s+, et que j’appelle invariablement un alcalino-terreux même s’il s’agit de He. Réf. 9, 10.

Cela m’a encouragé à passer outre à ma prévention ci-dessus et à envisager une 2^e période contenant Li et Be et des périodes se terminant sur un alcalino-terreux. Le caractère de l’élément au début d’une période varie selon la strate, il est le même pour les 2 périodes d’une strate. Une raison de symétrie supplémentaire se présente : dans une période de la nouvelle écriture, la valeur de l est fonction décroissante de z et la valeur de n est fonction croissante de z.

J’ai alors modifié mon 2^e postulat et je me suis attaché à 120 pour le nombre d’éléments. Ce nombre est remarquable car il est le produit des 5 1ers nombres : 1X2X3X4X5 = 120. Regardez non les lis des champs mais les doigts de la main. Fig. 13.

Fig. 13. De ma main gauche. Le produit des 5 premiers nombres est égal à 120.

Le québécium perd son attrait de dernier élément de la liste, mais conserve celui de dernier gaz rare. Le dernier élément z=120 appelé officiellement et temporairement Ubn pourrait s’appeler Janetium symbole Jt.

Janet l’anticipateur a donc prévu dès 1928 la répartition de la suite des éléments telle que je la propose : huit lignes que j’appelle des périodes, qu’il a montrées formant des paires ayant même longueur, auxquelles il n’a pas attaché une appellation , que j’appelle des strates. Cela se trouve dans notre point de départ Fig. 1.

Reste à trouver le pourquoi des strates assurant la symétrie 4 du tableau. On l’appelle universellement périodique et elle l’est à sa manière, mais cette appellation sécurisante a peut-être empéché qu’on découvre plus tôt une réécriture convenable révélant sa symétrie. Je crois opportun de conserver l’appellation historique de système du québécium, ce qui est son nom de baptême, mais de parler au besoin de tableaux symétriques des éléments.

J’ai proposé en 2004 une explication fondée sur les cônes de précession virtuels des spins des électrons caractéristiques appartenant aux éléments successifs. En plus du doublage imaginé par Pauli et lié aux spins – et +, il existerait une tendance au quadruplage, 4 spins s’engageant dans une structure saturante, géométriquement identique à celle qui détermine la prolifération, si utile à la vie, des structures tétraédriques du carbone. Réf. 11, 13, 14.

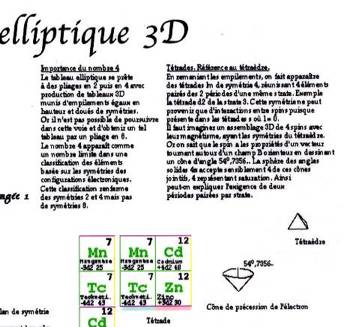
Fig. 14. Extrait page 17 de Réf. 13. Je propose d’attribuer un cône de précession d’ouverture 109,471o = 2arccos(1/√3) à l’électron caractéristique de chacun des éléments d’une tétrade (ici Mn, Zn, Tc, Cd). Les 4 cônes accolés avec centres communs saturent la sphère des angles solides 4pi. Cette saturation est réalisée exactement et non sensiblement comme il est écrit. Saturation ne veut pas dire remplissage. Les axes des cônes et leurs faces planes décrivent un tétraèdre aussi bien que les 4 valences égales du carbone tétraédrique.

Conclusion.

Voilà. Le tableau de Janet-Scerri possède certaines symétries, mais surtout, il recéle des symétries latentes que la mise en équerres, suivie de manipulations géométriques, permet de mettre en évidence dans des présentations bi- et tridimensionnelles. Ces manipulations, à la lumière de la théorie du spin de l’électron, suggèrent un principe nouveau, doublement de celui de Pauli disant que les éléments existent en orbitales, càd par paires. Le principe nouveau dit que les éléments existent en tétrades associant 2 orbitales, càd par paires de paires.

La suite numérique des éléments dans le tableau est expliquée et s’établit ainsi : 4 strates de 2 périodes de même longueur chacune. Les strates successives renferment les nombres suivants d’éléments : 4, 16, 36 et 64.

J’ai montré quelques représentations logiques du tableau, d’autres encore sont possibles et s’ajouteront sans doute.

Civilités.

Éric Scerri m’ayant annoncé son passage prochain au Québec, cette annonce m’a conduit à porter une attention spéciale à son œuvre, consacrée en partie à l’étude des triades. La mienne est plutôt orientée vers les tétrades et je la lui soumets.

Je remercie mon fils Patrick Demers, expert-informaticien pour son, aide assidue.

Références.

1. Éric Scerri 2008, (Rôle des triades dans l’évolution du système périodique des éléments, au passé et au présent)

The Role of Triads in the Evolution of the Periodic System, Past and Present, Journal of Chemical Education, 85, 585-589, 2008

NDLR. Les triades représentent une sorte de symétrie.

2. Éric Scerri 2007, (L’héritage Mendéléévien : le système périodique) Mendeleev’s Legacy: The Periodic System, ©2007 Chemical Heritage Magazine, printemps 2007, Vol. 25, No 1

http://www.chemheritage.org/pubs//ch-v25n1-articles/feature_mendeleev_print.html

Traduction et soulignés NDLR.

Les règles gouvernant l’attribution des nombres quantiques furent rigoureusement expliquées par la théorie quantique, de sorte que les 2 1res couches contiennent au maximum 2 et 8 électrons – et on eut ainsi enfin une explication des longueurs des 2 1res périodes du tableau ! Des considérations semblables appliquées aux couches 3 et 4 annoncent 18 et 32 électrons respectivement, mais cela ne s’accorde pas avec la répartition des éléments dans le tableau périodique. Et c’est là tout un problème : la 3^e période contient 8 électrons au lieu de 18.

Tout compte fait, les nombres quantiques paraissent fournir une explication déductive satisfaisante du nombre total que chaque couche peut renfermer, mais en revanche la correspondance de ces valeurs avec les nombres d’éléments dans les périodes est en quelque sorte une coïncidence fortuite. L’ordonnance bien connue du remplissage des orbitales spdf* (*diagramme manquant) a été déterminée essentiellement de façon empirique.

Bohr a échoué à déduire l’ordre du remplissage des orbitales, et comme certains auteurs l’ont reconnu, c’est là un des grands problèmes de la mécanique quantique.

…

Concernant le système de Mendeleev, a question n’est plus de savoir s’il est valide, mais plutôt, de trouver quelle serait la meilleure manière de le représenter**…

…The rules that govern the assignment of quantum numbers are rigorously explained by quantum theory, with the outcome that the first 2 shells contain a maximum of 2 and 8 electrons—at long last an explanation for the lengths of the first two periods of the table! Similar considerations for the 3rd and 4th shells predict 18 and 32 electrons respectively, but this is not in accordance with the arrangement of the elements in the periodic table.

The problem is this: the third row of the periodic table contains 8, not 18, electrons. It turns out that while quantum numbers provide a satisfying deductive explanation of the total number of electrons that any shell can hold, the correspondence of these values with the number of elements that occur in any particular period is something of a coincidence. The familiar sequence in which the s, p, d, and f orbitals are filled (see diagram, left) has essentially been determined by empirical means. Indeed, Bohr’s failure to derive the order for the filling of the orbitals has been described by some as one of the outstanding problems of quantum mechanics.

…

The problem is no longer the validity of Mendeleev’s system, but the best way to represent it.

NDLR. ** La validité du sytème de Mendéléev est-elle vraiment hors de question ?La représentation serait-elle donc sans grande importance dans un système tel que celui de Mendeleev ? Un système représenté par un tableau est de ce fait nécessairement associé à la topologie et à la géométrie, et, de nos jours, à la théorie quantique ; toutes disciplines que j’invoque dans le système du québécium. L’introduction d’une représentation nouvelle peut conduire à réviser le système. - Il n’y a pas un tableau idéal unique, une multitude de tableaux sont possibles qui sont scientifiquement corrects, mais inégaux devant notre besoin de comprendre la structure de l’atome et en particulier sa symétrie d’ordre 4. Le système du québécium et ses tableaux, à la différence de ce qui était admis jusqu’ici, mettent en évidence pour la 1^re fois cette symétrie et annoncent une compréhension meilleure de l’organisation de l’atome.

Fig 15. Système du québécium. Tableau elliptique d’après Réf. 3 ACFAS. Il démontre une symétrie double miroir des valeurs l et m. Réf. 5, 6, 7, 8.

Tableau périodique elliptique_2.png

Réf. 3. Pierre Demers 2004, Un jeu de blocs qui enseigne la nouvelle classification des éléments Chapitre 3, LeSystème du Québécium, 2^e édition,

http://www.lisulf.quebec/QbSyst2e.23quater.html,; même titre, projet ACFAS, http://www.lisulf.quebec/ACFAS2004jeublocsQb.html

Fig. 16. Boîtes cubiques. Archives Alpha Plastiques 1998.

Réf. 4. Alpha Plastiques 1998, Mémoire, boîte cubique 14 1/4 d’arête, daté de septembre 1998. Boîte employée à l’époque tableau 3D de 120 boules Fig. 10. - Fig. 16.

Réf. 5. Pierre Demers 2010 (Pierre Demers 1997), Système du Québécium, Le tableau périodique des éléments est un double miroir, à venir

Réf. 6. Pierre Demers 1997), Système du Québécium, Le tableau périodique des éléments ISBN 2-9802454-4-5, PUM 4e trimestre 1997, traduction interdite,

Réf. 7. Pierre Demers 2004, Système du Québécium La nouvelle classification des éléments, ISBN 2-9802454-7-X, PUM 2e trimestre 2004, traduction interdite,

Réf. 8. Pierre Demers 2004, Système du Québécium La nouvelle classification des éléments, ISBN 2-9802454-7-X, PUM 5. Pierre Demers 2010, Système du Québécium, traduction interdite, site : http://www.lisulf.quebec/quebecium.html

Réf. 9. Loïc Casson 2009, CTHS, 134e congrès, Bordeaux, 2009 ,
Célèbres ou obscurs. Hommes et femmes dans leurs territoires et leur histoire Charles Janet (1849-1932), un savant obscur en passe de sortir de l'ombre, http://cths.fr/co/communication.php?id=4009,

Réf. 10. Loïc Casson 2009, Charles Janet, un savant oublié, Soc. Académique de l’Oise, Mémoires, Mars 2008,

http://soc.acad.oise.free.fr/bulletin.htm

loic.casson@infonie.fr

Réf. 11. Pierre Demers 2005, Système du Québécium, Cônes de précession du spin des électrons. Tétrades de cescônes, http://www.lisulf.quebec/PrecessionSpinhtml, 18-Dec-2005
 

Réf. 12. Pierre Demers 2007, Système du Québécium. Géométrie quantique */**

http://www.lisulf.quebec/GQ1sur2, 28-Jan-2007

Réf. 13. Pierre Demers 2004, Système du Québécium Le Tableau elliptique des éléments par Pierre Demers. Une collection de tableaux, ISBN 2-9802454-8-8, PUM2004

http://www.er.uqam.ca/nobel/c3410/Catalogue11XII2004.html

Réf. 14. Pierre Demers 2010 Système du Québécium. Le tétraèdre dans la classification des éléments chimiques. Une note historique. Une version nouvelle du tableau tétraédrique des éléments,12-26I2010 QbtetraNveau.htm

-30-