EquiSphere.html
http://www.lisulf.quebec/GQ2sur2html Suivant : http://www.lisulf.quebec/GQ1sur2 Précédent : http://www.lisulf.quebec/Atomesentetradeshtml http://www.lisulf.quebec/PrecessionSpinhtml Quebecium http://www.lisulf.quebec/quebecium.qc.ca
Système du Québécium.
Équipartition de la sphère
Pierre Demers
Le problème posé
L'examen des cônes de la précession du spin de l'électron dans le système du québécium a conduit à formuler et à résoudre un problème nouveau de la géométrie de la sphère et de la trigonométrie sphérique, concernant les triangles sphériques. Voir PrecessionSpin.html.
Combien de triangles sphériques équilatéraux égaux peut-on tracer sur la surface d'une sphère, occupant la totalité de sa surface?
L'examen mentionné a montré que le nombre 4 est une solution. Il reste à généraliser.
Le problème général est celui-ci. Combien de polygones réguliers semblables et égaux peut-on tracer sur la surface d'une sphère, occupant la totalité de sa surface?

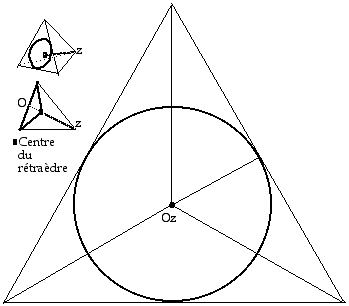
Fig. 1. Un cercle inscrit sur une face d'un tétraèdre régulier. Il détermine un cône d'ouverture 109,471o, lequel est tangent par une génératrice à un 2e cône semblablement inscrit sur une autre face, semblablement à un 3e et à un 4e cônes. De la sorte, le tétraèdre est occupé par 4 cônes traçant 4 cercles sur ses faces. Les sommets des cônes sont au centre du tétraèdre. Les 4 cônes réunis forment une tétrade.
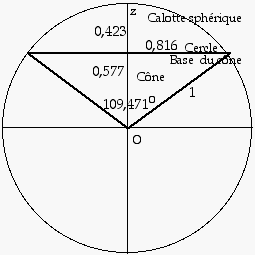
Fig.2. Coupe du cône d'ouverture 109,47 degrés placé dans une sphère des angles solides
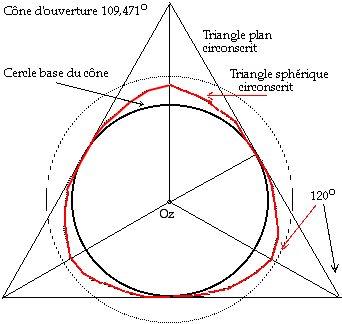
Fig. 3. Le cône d'ouverture 109,471o. Vue dans le plan contenant la face plane circulaire base du cône. Dans ce plan, le triangle plan circonscrit au cercle base du cône. En rouge, triangle sphérique circonscrit à ce cercle, lequel triangle est tracé sur la surface de la sphère, dont le contour est le grand cercle en pointillé. L'hémisphère inférieur ne paraît pas
Nombre 4
La théorie quantique du vecteur spin 0,5 de l'électron a conduit à lui attribuer une propriété géométrique remarquable. Voir PrecessionSpin.html. En présence d'un champ magnétique d'axe Oz, ce vecteur s'oriente obliquement par rapport à ce champ en conservant un angle thêta constant, égal à 54,735o. Il tourne autour de l'axe Oz en traçant dans l'espace un cône de cet angle, d'ouverture 109,471o. Or ce cône, si on place son sommet au centre d'un tétraèdre régulier, inscrit sa base circulaire dans une face du tétraèdre, dont l'angle dièdre est le complément de 109,471o soit 70,529o. Si de plus le sommet du cône est placé au centre d'une sphère des angles solides, il y détermine un cercle et un triangle sphérique.
Le tétraèdre et la sphère peuvent recevoir 4 tels cônes déterminant 4 triangles sphériques. Les angles trièdres à la rencontre des grands cercles sur la sphère valent tous 120 degrés.

Fig. 4 Continue la figure 3. Montre 4 triangles sphériques occupant la totalité de la sphère. Ce qui est en pointillé est tracé sur l'hémisphère inférieur vu par dedans. Les lignes définissent 4 triangles sphériques a, b, c, d occupant dans son entièreté l'angle solide 4¹ stér, chacun occupant ¹ stér. Des cercles inscrits dans ces triangles, trois apparaissant comme des ellipses sont ceux des bases de 3 cônes. Les 6 points de tangence entre cercles sont marqués par les 6 binômes tels que b3d2., qui marquent aussi les rencontres entre triangles. En ces points. l'angle dièdre extérieur est 109,471 +180 degrés, l'intérieur est le complément de 109,47 soit 70,53 degrés. - On montre le tracé, partiellement en bleu, du tétraèdre passant par les cercles bases des cônes. Il exclut 4 calottes sphériques.
Le nombre 4 donne une réponse affirmative, or cette réponse affirmative est associée au tétraèdre régulier, lequel est un polyèdre de Platon formé de 4 faces planes triangles égaux. Cela suggère d'examiner le cas des nombres associés aux autres solides de Platon de faces triangulaires, qui sont l'octaèdre et l'icosaèdre, soit les nombres 8 et 20. Intuitivement, la réponse paraît dès lors affirmative pour les nombres 8 et 20.
Le cas général. Solides de Platon. La condition platonicienne
Reprenons le problème général. Combien de polygones sphériques réguliers et égaux peut-on tracer à la surface d'une sphère, occupant la totalité de la surface 4¹ stéradians
Ce nombre est n et les polygones ont m côtés.
Supposons que nous ayons réussi à réaliser l'équipartition désirée avec n polygones sphériques équilatéraux égaux. À l'intérieur de chacun, traçons le cercle circonscrit, puis autour de chacun de ces cercles, traçons le polygone plan circonscrit. Nous obtenons dès lors une figure fermée, un solide formé de n faces polygonales égales. Or ce solide ne peut être que l'un des 5 solides convexes de Platon. Appelons ce résultat la condition platonicienne. Les possibilités reconues sont comme suit.
n nombre de polygones inscrits
....m nombre de côtés de chaque polygonen = 4 triangles, ayant chacun m = 3 côtés pour le tétraèdre
n = 8 triangles, ayant chacun m = 3 côtés pour l'octaèdre
n = 20 triangles, ayant chacun m = 3 xôtés pour l'icosaèdre
n = 6 carrés, ayant chacun m = 4 côtés pour le cube
n = 12 pentagones, ayant chacun m = 5 côtés pour le docécaèdre
Et la liste est close.
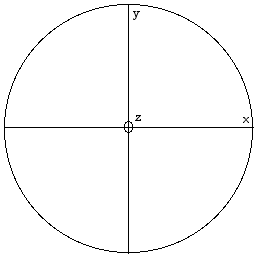
Fig. 5. Une sphère divisée en 8 octants triangulaires égaux, sa surface en 8 triangles sphériques égaux, équilatéraux et trirectangles. On peut inscrire un cône dans chacun d'eux, d'ouverture 70,529o.
Nombre 8
Ce nombre est recommandé à cause de l'existence de l'octaèdre régulier formé de 8 triangles égaux. Mais la recommandation est en quelque sorte superflue, parce qu'il apparaît naturellement dans la division et le marquage des globes terrestres. On inscrit les 3 grands cercles selon le trièdre des coordonnées xyz. On obtient 8 triangles sphériques équilatéraux et trirectangles. Fig. 4
Dans chaque octant, on peut inscrire un cône tangent aux 3 faces x = 0, y = 0, z = 0. Son ouverture est 70,529o, et cet angle est le complément de 109,471o.
Nombres impairs
Un raisonnement simple exclut un nombre impair de triangles ou de pentagones Pour que la structure soit symétrique, chaque côté d'un triangle doit être commun avec un côté d'un autre triangle. Cette condition requiert que le nombre total des côtés chez les triangles présents soit pair. Par exemple, trois triangles ont un total de 9 côtés et dans leur assemblage, il restera nécessairement un côté célibataire. Cela reste vrai pour des pentagones.
Donc nombres impairs exclus dans le cas des triangles et des pentagones, ce qui s'accorde avec la condition platonicienne.
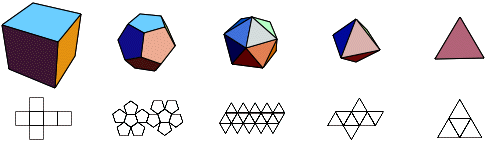
Fig. 6. Les solides réguliers ou de Platon. Merci Wolfram.
Conclusion
Les nombres possibles sont 4, 6, 8, 12 et 20.
Le problème posé peut paraître élémentaire mais n'apparaît pas dans le traité de Dalle sur la trigonométrie sphérique, ni dans l'étude de Maurice Starck. sur les polyèdres.
http://www.ac-noumea.nc/maths/amc/polyhedr/p_sphere.htm
Cônes inscrits
Dans une face polygonale d'un polyèdre de Platon, on peut inscrire un cercle, qui servira de base à un cône qui a son sommet au centre du solide, dont la génératrice a son extrémité au milieu d'une arête. Le cône est défini par la longueur rhô de sa génératrice et par la distance r de sa base au centre du solide. Voici l'ouverture 2thêta de ces cônes pour les 5 solides qui nous intéressent.

Fig.6pq. Cône inscrit dans une face d'un polyèdre de Platon.
Tableau (d'après Wolfram)
Cônes inscrits dans les faces des polyèdres de Platon. Arête = 1
..................................r.....................rhô.........2thêta = 2arccos(r/rhô)
Tétraèdre.........0,20412.............0,35355..............109,471deg.
Cube.................0,5.....................0,70711................90
Octaèdre...........0,40825.............0,5........................70,528
Dodécaèdre......1,11352.............1,13092................63,435
Icosaèdre..........0,75576..............0,80902................41,812
On trouve un répertoire utile.
http://mathworld.wolfram.com /PlatonicSolid.html
EquiSphere
http://www.lisulf.quebec/GQ2sur2.html Suivant : http://www.lisulf.quebec/GQ1sur2.html Précédent : http://www.lisulf.quebec/Atomesentetrades.html http://www.lisulf.quebec/PrecessionSpin.html http://www.lisulf.quebec/quebecium.html30