Fichier23bishtml

Le québécium avec ses 118 électrons et l'hydrogène avec son électron unique se ressemblent en deux points : ils sont l'un et l'autre des atomes et leur états électroniques ont des caractères décrits par des quadruplets de nombres quantiques n, l, m, s. Dans le cas de H, il faut ajouter le nombre j, variable dépendante de l et de s dont elle est la somme. Une autre ressemblance est qu'il y a plusieurs états ordonnés à considérer dans H et dans Qb.

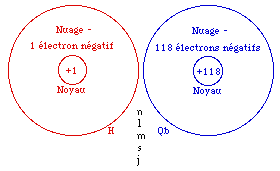
FIG. 2. Schéma comparatif des états H et Qb.

La dissemblance est au moins quintuple :

1o les états de H sont l'état fondamental au repos et des états excités, tandis que les états de Qb sont des états au repos;

2o les états de H sont accessibles successivement alors que ceux de Qb sont simultanés;

3o les états de H concernent un seul électron, alors que ceux de Qb concernent chacun l'un de plusieurs électrons.

4o Dans H, l et s sont couplés pour donner le nombre quantique j valant l±1/2, tandis que ce couplage est inexistant dans Qb. Dans Qb, l et s interviennent séparément.

5o Et surtout, le nombre m n'intervient pas dans H.

Examinons de plus près le répertoire des états de H en le comparant avec celui de Qb. Figure 2, Tableau 1.

L'intervention de m dans Qb crée la grande différence entre H et Qb. En l'absence de cette intervention, voici la suite imaginaire des états de Qb, qui seraient définis par n, l, s. Tableau 2.

No d'ordre

1 à 10

11 à 20

21 à 30

31 à 40

La différence entre H et Qb tient surtout à l'effet multiplicateur de m. Cet effet augmente d'un facteur 2l+1 le nombre d'états de nombre quantique azimutal l. Ainsi l'état 4f- dans le tableau ci-dessus est remplacé par 7 états, de 4f-3- à 4f3-. Le Tableau 4 rappelle l'alphabet quantique des électrons.

s pour l = 0

p pour l = 1

d pour l = 2

f pour l = 3

La différence entre H et Qb tient aussi au caractère simplet des états s de H. Dans les états p, d, f etc, l'interaction entre l et s fait que le spin s'oriente de deux façons, de sorte que j vaut l-1/2 ou l+1/2. Ces états sont des doublets. Il n'en est pas ainsi dans les états s, où l = 0. Ceux-ci sont des simplets. Le nombre j des états s prend la valeur 1/2 en valeur absolue et il n'intervient que par sa valeur absolue.

La liste du Tableau 2 n'est pas purement imaginaire. Elle correspond en réalité à celle des demi sous-couches de Qb et des atomes de la colonne vertébrale. Les entrées s'y succèdent par doublets, à la manière des partenaires d'une orbitale, ne différant que par le signe représentant le spin. La liste contient ainsi 19 doublets. Chaque entrée de cette liste est multipliée dans la réalité, en nombre d'états et d'éléments, par un facteur 2l+1. Ce facteur correspond à une sorte d'interpolation entre les entrées de la colonne vertébrale.

Voici maintenant la liste ordonnée des états que l'on observe pour H, arrêtée à 7p+. Ils sont définis par n, l et s. Sauf les états s qui ont l = 0, les deux valeurs possibles de s font qu'il y a deux états associés à une paire de valeurs n, l ; on dit pour cette raison que ces états de H sont des doublets. Pour les états s, on a écrit par convention et anticipation le signe ±. Tableau 5.

En 2e ligne, la valeur de j. Souligné : absent du québécium.

No d'ordre

1 à 1 0

11 à 20

21 à 30

31 à 40

Source :

Dans une théorie élémentaire de l'atome H de Schrödinger, les états de même valeur de n seraient indiscernables entre eux et indifférents aux valeurs de s, l ou j : l'ordre ne dépendrait que de n. Dans une théorie plus avancée due à Pauli et Dirac, l'ordre dépendrait de n et de j. Finalement, la théorie de Lamb explique que l'ordre dépend de n, l et s.

L'ordre expérimental des états est en fait souvent indifférent, les valeurs de j étant les mêmes. Cette circonstance est indiquée par un signe = (égale). Elle concerne un double quadruplet d'états p, d, f et g et un double quadruplet d'états p, d, f, g et h.

À première vue, la correspondance entre les listes H et Qb (Tableaux 3 et 5) n'est que partielle et approximative parce que l'ordre des entrées n'est pas le même. Tout au plus peut-on reconnaître une progression générale du numéro d'ordre avec les valeurs croissantes de n et de l. La liste H n'a que 39 entrées malgré que les valeurs de l y atteignant 5, et la liste Qb a 118 entrées malgré que les valeurs de l n'y dépassent pas 3. La grande différence des populations résulte surtout de l'effet multiplicateur de m, inexistant dans H.

Voyons toutefois les ressemblances. Aux signes près, cette liste de 39 entrées de H renferme les 19 doublets de la liste imaginaire plus haut en plus de 8 termes f, g et h absents du québécium. Les signes manquants sont ceux de 7 états s, présents avec le seul signe ±.

On peut réfléchir à ces ressemblances et dire : le tableau imaginaire du québécium Qb se comprendrait comme un remaniement du tableau de l'hydrogène.

Il faudrait doubler les états s±. Le doublage des états s± se comprend physiquement. Dans l'atome d'hydrogène, le champ du seul proton ne suffit pas pour que le spin, seul constituant du moment cinétique j dans un état s, puisse prendre les 2 états - et +. Dans un atome ayant au moins un autre électron, le champ de ce dernier suffit pour que les deux états - et + se manifestent.

Le caractère doublet des états autres que s de l'atome d'hydrogène s'explique par le champ résultant du moment cinétique non nul associé à l non nul, agissant sur le moment cinétique du spin : celui-ci prend dès lors l'une des deux valeurs - ou +.

Il faudrait exclure les états superflus mentionnés, dont aucun analogue n'apparaît dans la formule de Qb.

Il faudrait multiplier les états p, d, f par le facteur 2l+1. Cela se rattache évidemment aux effets Zeeman et Stark discutés au paragraphe suivant. Ces effets produisent ce qu'on appelle une levée de la dégénérescence.

Il y a 31 états pertinents dans le Tableau 5 de H. En tenant compte du doublage des états s et de la multiplication mentionnée, voici la liste des états de Qb auxquels on passerait en partant de ces 31. On trouve bien les 118 états de Qb, mais pas dans l'ordre correct. Tableau 6. Les demi sous-couches se présentent en paires de même composition sauf que l'une a le spin - et l'autre le spin +.

Les 31 états de H pertinents. No des lignes de 1 à 38

Comment pourrait-on justifier le remaniement nécessaire pour atteindre l'ordre correct? Une réponse après le prochain paragraphe.

La théorie quantique attache à l'atome d'hydrogène les 4 nombres mentionnés plusieurs fois précédemment : n, l, s et m. Elle déclare que le nombre m, appelé quantum magnétique, peut prendre les valeurs suivantes.

Si l = 0 , état s : m = 0.

Si l = 1, état p : m = -1, 0 ou 1.

Si l = 2, état d : m = -2, -1, 0, 1 ou 2.

Si l = 3, état d : m = -3, -2, -1, 0, 1, 2 ou 3.

etc.

En général, le nombre de valeurs possibles de m est 2l+1. Pour des valeurs données de n, l, s, la théorie prévoit autant d'états distincts que de valeurs de m, soit 2l+1 états.

Mais elle prévoit aussi que, dans l'atome d'hydrogène isolé d'influences extérieures, ces 2l+1 états sont confondus en un seul, on dit d'eux qu'ils sont dégénérés. Leur existence est certaine, mais ils sont alors indiscernables. Leur existence collective peut toutefois se manifester par des poids statistiques dans certaines expériences.

Elle prévoit enfin que si on soumet l'atome d'hydrogène à des influences extérieures appropriées, les 2l+1 états deviennent distincts. C'est ce qu'on appelle une levée de la dégénérescence.

L'expérience a montré que la théorie ci-dessus est valable pour n'importe quel atome dont on a excité un électron : cet électron excité se comporte alors, quant à la dégénérescence et à sa levée, comme il est décrit pour l'électron de l'atome d'hydrogène.

La théorie a expliqué les résultats sur la levée de la dégénérescence dans un champ magnétique, découverte par Pieter Zeeman en 1896. C'est l'effet Zeeman. Elle a aussi expliqué la même levée par un champ électrique ou effet Stark découvert en 1913.

Il est bien évident que la levée de la dégénérescence à l'intérieur des atomes explique pourquoi on observe une multiplication du nombre d'états par un facteur 2l+1 entre les entrées du Tableau 5 de H et celles du Tableau 3 de Qb.

Le champ de force levant de la dégénérescence dans un atome est de nature électromagnétique et assimilable à la fois au magnétisme et à l'électrostatique. Ce champ s'exerçant sur chaque électron dépend du noyau et de tous les autres électrons présents.

La grande différence entre les états de l'hydrogène et ceux du québécium résulte d'une levée de la dégénérescence par effet Zeeman-Stark (ou en abrégé effet Zeeman) à l'intérieur du québécium, résultant du champ de forces intra-atomiques. Les forces intraatomiques sont sans doute pour une part des forces d'échange étrangères à l'électromagnétisme classique, comparables à celles des liaisons covalentes par mise en commun d'électrons entre 2 atomes.

Cette levée de la dégénérescence justifie, dans le Tableau 6, le passage des 31 états H aux 118 états Qb pour ce qui est des états p, d et f; quant aux états s, leur doublage a été expliqué plus haut.

Dans la perspective du système du québécum, nous allons voir qu'on explique facilement le remaniement et la mise en ordre nécessaires pour passer de l'ordre dans le Tableau 6, qui représente une 1re étape, à celui du Tableau 3 du québécium. Ce sera une 2e étape de la genèse du québécium, étape finale, et il s'agit d'une genèse constructive.

FIG. 3. Grille vide indéfinie.

Voici le procédé, qui met en vedette le nombre magique 4. Nous nous donnons d'abord une grille vide indéfini. FIG. 3.

Principe 0 : cheminer dans l'ordre des numéros d'ordre du Tableau 5, une demi sous-couche à la fois, inscrite en équerre. Il se trouve qu'on rencontre invariablement la demi sous-couche de spin - avant sa partenaire de spin +.

Principe 1 : augmenter une équerre - une fois installée de sa partenaire de signe + en regard.

Au besoin, sauter des termes et les employer dans la suite.

Principe 2 : compléter les quadrants en regard.

Principe 3 : compléter une strate amorcée avant d'en amorcer une autre.

La grille du québécium avec sa structure apparaîtra. Les strates vont apparaître et se remplir dans l'ordre voulu.

Nous pourrions ajouter de compléter les orbitales, mais cela est effectivement réalisé par le principe 1. - Dès qu'un quadrant est installé, il amorce et définit une strate objet du principe 3.

Strate 1. Partant de l'état s± de H, nous avons 2 électrons, ce qui complète l'orbitale 1s, et satisfait au principe 1 puisque chaque électron constitue une équerre. Nous sommes rendus à Z = 2 He et nous avons obtenu 2 équerres d'une case chacune en diagonale. FIG. 4.

Une strate 1 est définie et réclame d'être complétée d'après le principe 3, ce qui exclut la participation de l'état 2p- qui contribuerait 3 états impossibles à loger dans la strate 1 qui n'a plus que 2 cases disponibles. Il faut donc sauter 2p-. FIG. 4.

Noter que He a trouvé tout naturellement sa place sans laisser de cases vides, alors que l'installer avec pour seul principe qu'il tombe à la fin d'une période conduit à laisser 16 cases vides.

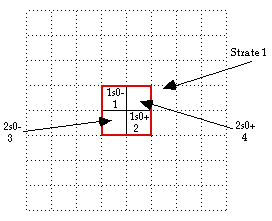
FIG. 4. La strate 1 est définie par l'installation de 1s0- et 1s0+ et ne peut être complétée que par 2s0- et 2s0+.

L'application du principe 3 de compléter la strate commencée ne peut se faire qu'en utilisant l'état 2s-et l'état 2s+ découlant de l'état 2s± de H. Nous avons dû sauter les 3 états issus de -2p, que nous ne pouvons pas loger dans la strate amorcée. Une tétrade est complète et remplit la strate. Nous sommes rendus à z = 4 Be. L'état 1s- a servi d'amorce au remplissage de la strate 1. FIG. 4.

FIG. 5. Installation d'une équerre 2p- et apparition de la strate 2. On ajoute l'équerre 2p+ opposée. Ensuite on complète les 2 quadrants opposés.

Strate 2. Nous rencontrons les 3 états 2p-, dont l'installation détermine une équerre, laquelle détermine une couronne et une 2e strate. FIG. 5.

Pour compléter la couronne, il faut d'abord augmenter l'équerre 2p- de l'équerre 2p+ de spin + opposé. Nous sommes rendus à Z = 10 Ne.

Pour compléter les quadrants, seuls des états s conviennent, et ce sont 3s- et 3s+.

Pour compléter le remplissage des 2 autres quadrants de la strate, il faut des états p et s, et ce sont les états 4p-, 4p+, 4s-, 4s+ qui conviennent. La strate 2 est remplie et nous sommes rendus à Z = 20 Ca. FIG. 6.

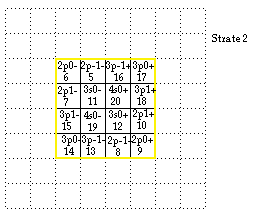
FIG. 6. Strate 2.

Strate 3. Par le cheminement principe 0, nous nous occupons de 3d- puis de 3d+ : cela introduit 10 états et nous sommes rendus à Z = 30 Zn. Par les principes 1, 2, 3, nous complétons la strate 3. Nous nous rendons à Z = 56 Ba en utilisant 4p-, 4p+, 5s- et 5s+, 4d-, 4d+, 6s- et 6s+. FIG. 7.

Noter que l'installation d'états d avec n = 3 après 19 K et 20 Ca n = 4 et non avant ces derniers se comprend naturellement dans le processus proposé et ne requiert pas d'hypothèse spéciale comme c'est le cas lorsqu'on considère les couches et non les sous-couches.

Strate 4. Puis nous rencontrons 4f- et 4f+, qui déterminent une grande couronne. En utilisant 5d-, 5d+, 6p-, 6p+, 7s-, 7s+ deux quadrants opposés se trouvent remplis. Puis la strate 4 continue de se remplir avec 5f-, 5f+, 6d-, 6d+, 7p-, 7p+ pour donner la formule complète de Qb 118.

Il reste 2 cases ou l'on placera 8s- et 8s+ afin de remplir la strate 4 et le tableau de 120 cases. FIG. 8.

Le résultat global paraît FIG. 9.

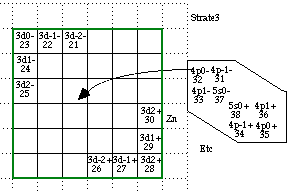
FIG. 7. Strate 3. Les équerres 3d- et 3d+ sont en place, il faut ajouter les équerres de l'encadré. etc.

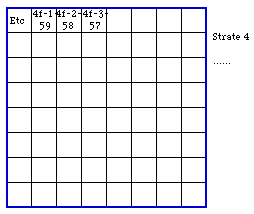
FIG. 8. Strate 4. Aperçu du remplissage. Voyez FIG. 9

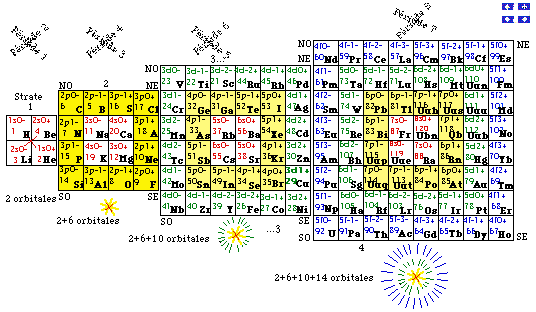
FIG. 9. La formule du québécium augmentée des états 8s0- et 8s0+, telle qu'obtenue par genèse constructive à partir des états de l'hydrogène.

D'après la référence

Auteur inconnu

la mécanique quantique indiquerait que les gaz rares auraient comme structure électronique des couches complètes, une couche complète signifiant tous les caractères permis avec un nombre quantique principal n donné. Or, il est bien connu qu'il n'en est rien sauf pour He et Ne. Voici la comparaison les valeurs réelles de z et les valeurs prévues "couches complètes de la mécanique quantique" des 6 gaz rares.

He2 et 2

Ne10 et 10

A18 et 28

Kr36 et 60

Xe54 et 110

Rn86 et 182

Les différences observées pour 4 des gaz rares sont énigmatiques.

Le système du québécium apporte une solution. Elle tient au principe de quadrature décrit ci-dessus et à ses exigences géométriques basées sur l'application d'un nombre magique égal à 4.

Voici un extrait de la référence mentionnée.

2001 Hachette Multimédia

Le modèle en couches

À l'échelle de l'atome (noyau + électrons), il existe également des nombres magiques d'électrons, pour lesquels les édifices atomiques sont particulièrement stables. Ainsi, la faible activité chimique des gaz rares (hélium, néon, argon, krypton, xénon, radon) indique que les électrons de ces atomes sont dans des configurations particulièrement stables. Leur énergie d'ionisation est notablement plus grande que celle des atomes voisins dans le tableau de Mendeleïev. 

Ces nombres magiques atomiques s'expliquent par la structure en couches de l'édifice. Les protons du noyau exercent une attraction sur les électrons, attraction qui, traitée par la mécanique quantique, fait apparaître des états quantiques accessibles aux électrons. Ces états quantiques sont groupés en paquets d'énergie voisine, appelés couches. À chaque fois que le nombre d'électrons d'un atome est tel qu'une couche est complètement remplie, l'énergie de liaison est plus grande.