Fichier26.html
Pédagogie du tableau elliptique
par Pierre Demers
![]()
FIG. 1. Un écrin elliptique enfermant la matière.
Classifier les éléments. 5 propriétés
Les éléments qui forment la matière se classifient commodément dans une grille formée de cases égales occupant une ellipse : c'est la classification elliptique des éléments. Chaque élément a un symbole et un nom. Exemples H hydrogène, Al aluminium, Mg magnésium, Pb plomb, U uranium.
La classification scientifique des éléments du présent tableau est basée sur certaines propriétés des atomes, peu immédiates mais satisfaisantes pour l'esprit et pour les applications, qui trouvent leur pleine explication en physique atomique.
Les propriétés générales des éléments telles la densité, l'aspect visuel et la température de fusion etc sont reliées aux propriétés atomiques, mais la théorie de ces relations est très incomplète.

FIG. 2. Schéma d'un atome.
Les propriétés atomiques qui nous importent sont au nombre de 5.
z. C'est le nombre atomique, nombre d'électrons contenus dans l'atome, égal au nombre de protons positifs du noyau de l'atome. Ce nombre identifie l'élément. Il vaut un nombre entier, de 1 à 120. Exemples H 1, He, 2, Al 13, Mg 12, Pb 82, U 92. La masse de l'atome, due principalement à celle du noyau, augmente avec z.
s, n, l et m. Les 4 autres propriétés sont connues par des expériences de spectroscopie. On les appelle nombres quantiques ou quanta, singulier quantum, en abrégé ce sont s, n, l et m, comme suit.
s est le quantum de spin ou spin; même si on l'appelle nombre, on le représente par un signe - ou +, ce dernier pouvant être omis. C'est un peu comme l'aiguille d'une boussole. Si on change l'aimantation de l'aiguille, elle inverse son orientation dans le champ magnétique de la Terre.
n est le quantum principal, il vaut 1, 2, 3, 4,, 5, 6, 7 ou 8. Certaines théories prétendent qu'il serait plus important que les autres nombres quantiques.
l est le quantum azimutal, il vaut 0, 1, 2 ou 3. Il est associé à certaines propriétés de distributions spatiales de l'électron dans l'atome.
m est le quantum magnétique, il vaut -3, -2, ,-1, 0, 1, 2 ou 3. Il est associé à des variantes des distributions spatiales de l'électron dans le champ électrique et magnétique à l'intérieur de l'atome.
Sans chercher la pleine signification de ces nombres, nous allons les employer. Le simple usage de ces nombres et de leurs permutations va nous permettre de comprendre mathématiquement la classification des éléments. Les nombres quantiques forment un code de 4 caractères, plus ou moins analogue à une foule de codes employés dans la vie courante, et ce code conduit à la géométrie des tableaux que nous allons décrire.
Le caractère nominal et sa notation.
À tout élément z est associé un code ou caractère électronique nominal, combinaison unique de s, n, l, m. Exemples.
H
...............-100He
...............100Mg
...............300Al
............... -31-1Pb
............... -610U
............... -530Seules certaines combinaisons des valeurs s, n, l, m sont réalisées.
Par commodité, on utilise des lettres au lieu de chiffres pour l, comme suit : s pour 0, p pour 1, d pour 2 et f pour 3. Par tradition, le signe représentant s est souvent placé en queue plutôt qu'en tête d'écriture. Noter le double emploi de s.
Finalement, la description nominale d'un élément comprend son symbole, les 4 nombres quantiques et la valeur de z. C'est ce qu'on inscrit dans une case de la grille (avec en plus le nom ). Exemples.
H
...............-100....1He
...............100....2Mg
..............300....12Al
............ -31-1....13Pb
.............. -610....82U
.............. -530....92Ou encore.
H
...............100-....1He
...............100+....2Mg
..............300+....12Al
............ 31-1+....13Pb
.............. 610-....82U
.............. 530-....92Et encore.
H
...............1s0-....1He
...............1s0+....2Mg
..............3s0+....12Al
............ 3p-1+....13Pb
.............. 6p0-....82U
.............. 5f0-....92Valence.
La valence décrit l'aptitude des atomes de se lier les uns aux autres. Elle vaut un nombre entier 0, 1, 2, 3... Dans la liaison électrochimique, un atome donne un électron et sa valence est électropositive, un autre atome capte un électron et sa valence est électronégative. Dans la liaison covalente, un atome met en commun son électron avec un autre atome.
La valence d'un atome dépend de son caractère.
Classification selon z.
La classification la plus répandue est celle créée initialement par Mendeleev en 1869. Elle est formée par la liste linéaire selon z avec alinéas inscrite dans une grille rectangulaire, chaque ligne porte le nom de période et les périodes sont inégales. Elle a 7 périodes occupant chacune une ligne dans sa partie principale et un supplément de 28 éléments occupant 2 lignes, soit 9 lignes au total. Chaque période se termine sur un élément de valence 0 qui est un gaz rare. Les périodes comprennent jusqu'à 18 groupes occupant chacun une colonne. En principe, les éléments d'un groupe ont tous des propriétés comparables, y compris la valence. On les appelle des congénères. FIG. 3
Elle a l'avantage de permettre un repérage commode selon Z et selon les colonnes pour sa partie principale. Seules les périodes 4 et 5 occupent exactement les 18 colonnes. Elle exclut 28 éléments de sa partie principale, laisse plusieurs cases vides et ne possède aucune symétrie. Elle met en évidence, quoique imparfaitement, les 4 nombres quantiques, sous l'aspect de blocs : s colonnes 1 et 2, d colonnes 3 à 12, p colonnes 13 à 18, f les lignes supplémentaires. Elle a suscité un intérêt universel, comme en témoigne son ubiquité.
Son aspect suggère un développement indéfini à mesure qu'on lit la suite des éléments, par l'addition d'éléments non encore réalisés ou spéculatifs, par exemple jusqu'à Z = 168.
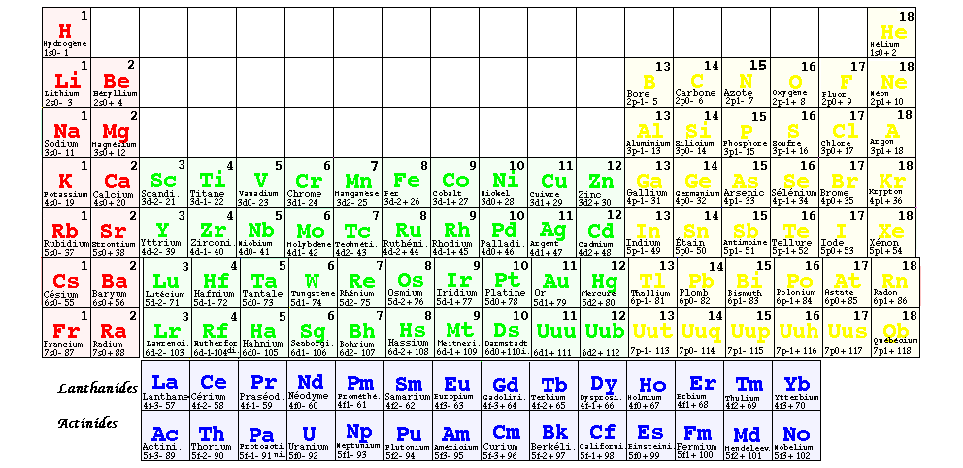
FIG. 3. Le tableau périodique des éléments de Mendeleev. 18 colonnes, lanthanides et actinides.
La classification elliptique en couches, selon n.
La classification nouvelle se base aussi sur les valeurs de z sans être une liste linéaire selon z avec alinéas. Cette liste est remplacée par une figure bidimensionnelle d'équerres emboîtées qui met en évidence les périodes, les groupes et surtout les nombres quantiques. Elle ne laisse aucune case vide et est parfaitement symétrique. La forme fermée de l'ellipse suggère une limitation au nombre d'éléments possibles. Jusqu'ici, 110 ou 112 des 120 éléments figurés ont été effectivement réalisés. Par symétrie, on y inclut les 2 éléments spéculatifs z = 119 et 120.
L'ellipse est uniquement définie. Demi petit axe 4,33, demi grand axe 10,33, l'unité étant le côté d'une case, rapport 0,419 = 1/2,39.
Plusieurs tableaux elliptiques sont possibles. Nous commençons par le tableau elliptique en couches c'est-à-dire selon n, n croissant d'ouest en est. En voici une analyse. FIG. 4
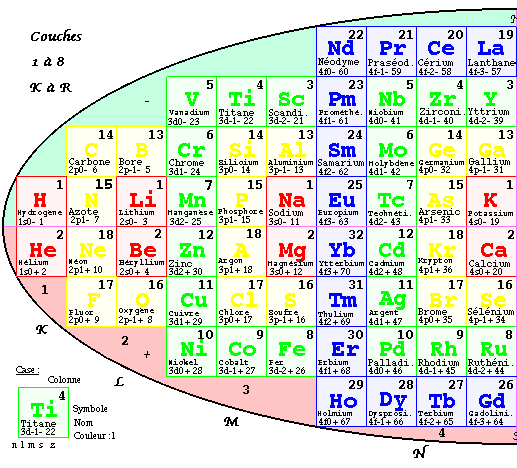
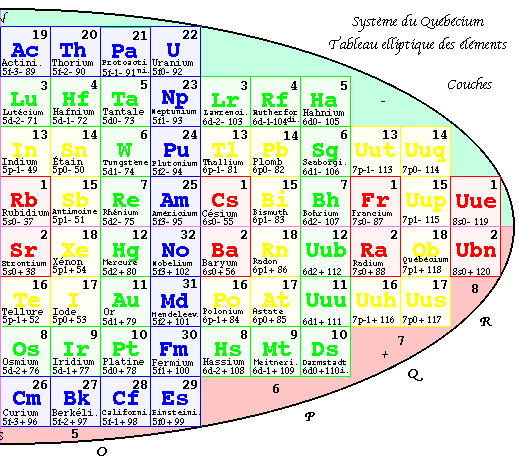
FIG. 4. Tableau elliptique des éléments par couches. De n = 1 à n = 8, de
K à R.Ce tableau est riche d'enseignements sur les structures électroniques des éléments.
Spin. Il y a 60 éléments - au nord de l'axe horizontal de l'ellipse et 60 éléments + au sud de cet axe (spin -, spin +). Tableau 1.
Tableau 1. Éléments par spin
60 éléments spin -
60 éléments spin +
Total 120 éléments
Quantum principal n, couches. On désigne les couches par les lettres majuscules K, L, M, N, O, P, Q, R. Chaque couche occupe un rectangle bicarré de grande dimension verticale. On reconnaît qu'il y a comme suit. Tableau 2
Tableau 2. Éléments par couche
2 éléments n = 1, couche K. Saturation = 2 éléments
8 éléments n = 2, couche L. Saturation = 8 éléments
18 éléments n = 3, couche M. Saturation = 18 éléments
32 éléments n = 4, couche N. Saturation = 32 éléments
32 éléments n = 5, couche O. Saturation = 50 éléments
18 éléments n = 6 , couche P. Saturation = 72 éléments
8 éléments n = 7, couche Q. Saturation = 98 éléments
2 éléments n = 8, couche R. Saturation = 128 éléments
Total 120, 8 couches. Saturation = 408 éléments
La présence d'un maximum réparti sur n = 4 et 5, à mesure qu'on lit les nombres ci-dessus, suivi d'une décroissance symétrique, suggère qu'il y a une limite au nombre d'éléments possibles. Une théorie prévoit que les couches pourraient contenir le nombre d'éléments indiqués dans la colonne saturation. Les couches K, L, M, N sont saturées, les couches O, P, Q et R ne le sont pas.
Quantum azimutal l, sous-couches. Une sous-couche est définie par un doublet de valeurs n et l. Les valeurs de l sont représentées par des couleurs, comme suit.
Tableau 3. Type de sous-couches et couleur
l = 0, éléments s, R rouge
l = 1, éléments p, J jaune
l = 2, éléments d, V vert
l = 3, éléments f, B bleu
Ainsi sont mises à contribution les 4 couleurs fondamentales de la perception visuelle.
Tableau 4. Éléments par sous-couche
16 éléments en 8 sous-couches s
36 éléments en 6 sous-couches p
40 éléments en 4 sous-couches d
28 éléments en 2 sous-couches f
Total 120 éléments en 20 sous-couches
Équerres et demi sous-couches. Chaque sous-couche est présente en 2 demi sous-couches, chacune sous l'aspect d'une équerre symétrique. Une équerre a 2 bras égaux et le nombre de cases dans chaque bras est égal à l, soit comme suit. Nous disons par extension que les cases isolées l = 0 sont des équerres de bras nuls. Tableau 5.
Tableau 5. Éléments par demi sous-couche ou par équerre
16 éléments en 16 demi sous-couches s
36 éléments en 12 demi sous-couches p
40 éléments en 8 demi sous-couches d
28 éléments en 4 demi sous-couches f
Total 120 éléments en 40 demi sous-couches
Les équerres s'emboîtent et déterminent des carrés et des rectangles. Dans ces emboîtements, les valeurs de l augmentent du centre vers la périphérie.
Invariants de la classification des éléments. Les demi sous-couches et les équerres les figurant graphiquement sont les constituants invariants de la classification des éléments dans le système du québécium. Ces constituants peuvent être agencés de nombreuses façons mais leur composition et leur ordonnance interne doivent rester inchangées. Certaines de ces façons conduisent à un tableau elliptique. Il y a un total de 40 tels invariants, que l'on peut reconnaître FIGURE 3, leur sommaire Tableau 5. Un de ces invariants est la demi sous-couche (Sc Ti V Cr Mn, d'autres sont (B C N), (Te I Xe) etc
Quantum magnétique m. m forme la variable courante dans les cases. Ses valeurs se répètent, elles sont des entiers algébriques compris entre -3 et 3, 0 permis. Voici un sommaire de ces valeurs. Tableau 6.
Tableau 6. Sommaire des valeurs de m
4 éléments m = -3
12 éléments m = -2
24 éléments m = -1
40 éléments m = 0
24 éléments m = 1
12 éléments m = 2
4 éléments m = 3
Total 120
On note la présence d'un maximum, à mesure qu'on lit les nombres ci-dessus, suivi d'une décroissance symétrique.
Épine dorsale. Avec la disposition choisie, le maximum algébrique de m de chaque équerre tombe dans une case voisine de l'axe OE et forme ce que nous appelons l'épine dorsale de la classification. L'épine dorsale renferme 40 cases ou 40 éléments qui possèdent une stabilité électronique particulière. Aucun de ces éléments ne constitue une exception. Voir le Fichier 22 du présent disque compact.
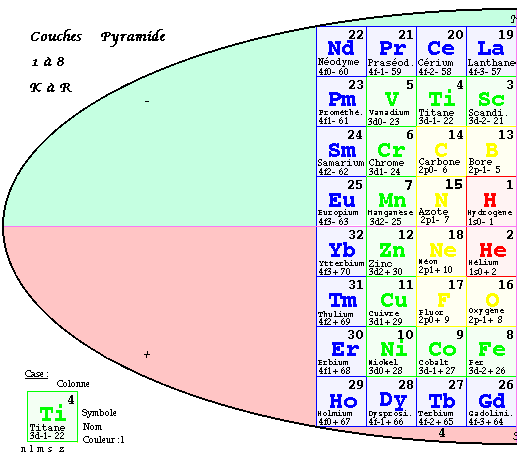
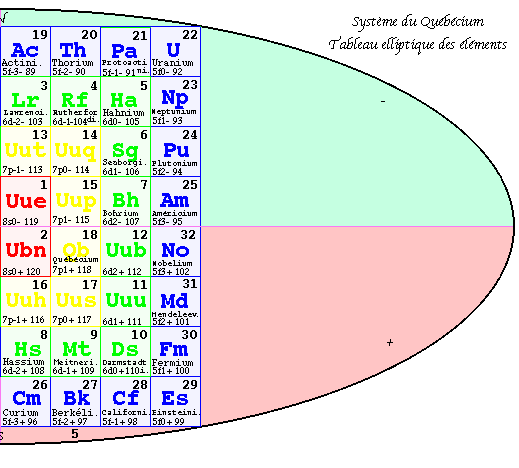
FIG. 5. Plan de la 1re pyramide, couches, 3D.
Première pyramide 3D.
L'inspection du contenu de l'ellipse suggère naturellement de déplacer les couches 3 et 6 (
M et P) et de les placer jointivement sur les couches 4 et 5 (N et O), en superposant les couleurs semblables. On fait semblablement pour les couches 2 et 7, puis 1 et 8. Si les cases planes ont été remplacées par des cubes vus en projection plane, la forme 3D est une pyramide à base quadrangulaire ayant un axe vertical et sa vue en projecion plane est une grille carrée de 64 cases, de 8 cases de côté inscrite dans l'ellipse. Les équerres de même couleur sont superposées. FIG. 5Chaque case de ce plan désigne une colonne monochrome de hauteur 1, 2, 3 ou 4 cases cubiques. Les colonnes de même couleur sont jointives et forment 4 blocs : couleurs R, J, V, B. Le bloc central R est massif, les autres sont des couronnes. Les couches vont de K à N en descendant à l'ouest, puis de O à R en remontant à l'est.
Dans cette 1re pyramide, l'ordre suit ainsi les valeurs de n.
On y trouve au même niveau des valeurs de z disparates, qui ne sont pas toutes consécutives. Par exemple, les cases z = 1 et z = 119 sont jointives. En remaniant le contenu de la première pyramide, on peut ordonner les cases par valeurs croissantes de z de haut en bas.
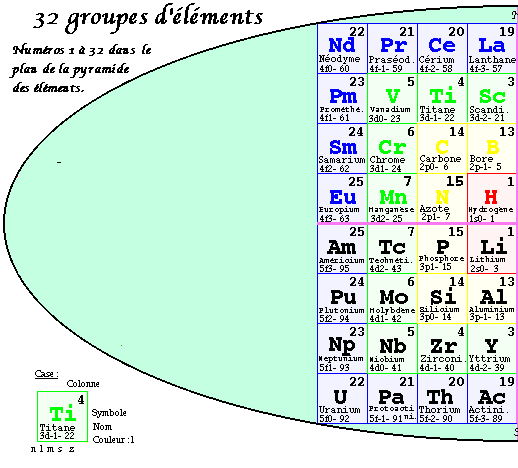
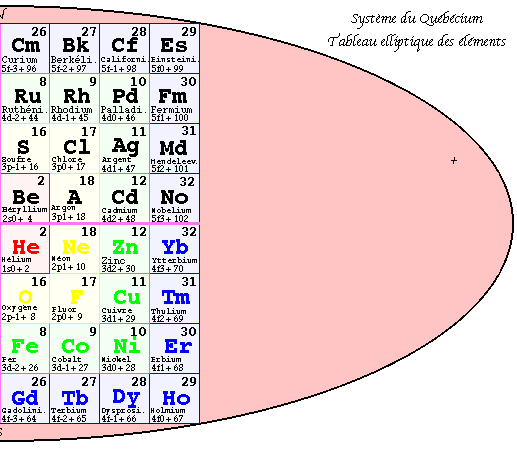
FIG. 6. 2e pyramide, plan, les 32 groupes.
Deuxième pyramide 3D. Les strates.
Dans la 2e pyramide, les valeurs de z se trouvent ordonnées régulièrement. On a permuté entre elles les équerres sans changer leur contenu et en les laissant à l'intérieur du bloc coloré auquel elles appartiennent. Les équerres de valeurs de z consécutives et de même valeur de n se trouvent en regard par rapport à l'axe vertical.
Dans le plan de cette pyramide, les valeurs les plus petites de z apparaissent dans les cases centrales : 1, 2, 3 et 4. se trouvent en regard 2 à 2. Elle possède 4 niveaux appelés strates, numérotées de 1 à 4 en commençant par le haut. Ainsi les strates contiennent les nombres suivants de cases cubiques.
4 dans la strate 1
16 dans la strate 2
36 dans la strate 3
64 dans la strate 4
Total 120.
Voici une analyse du contenu de ce tableau.
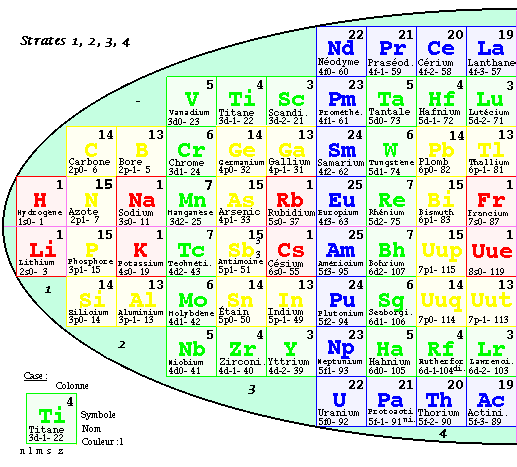
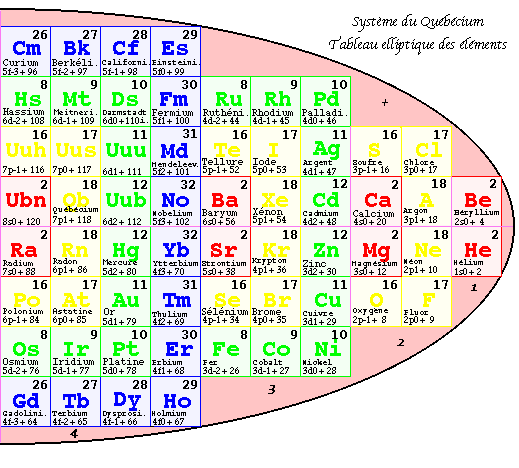
FIG. 7. Tableau elliptique, les strates.
Tableau elliptique par strates.
Par une opération inverse de celle qui a donné naissance à la 1re pyramide, il est facile de séparer la 2e pyramide selon les strates, partie ouest à gauche, partie est à droite, et de retrouver un tableau 2D semblable au tableau original, mais avec des cases occupées de façon nouvelle : c'est le tableau elliptique par strates.
Selon s.
Il y a 60 éléments - à l'ouest de l'axe vertical de l'ellipse et 60 éléments + à l'est de cet axe. Total 120 éléments.
La distribution des signes dans le tableau par couches était nord sud, ici elle est ouest est. Les quadrants NO et SE ont gardé leurs signes.
Selon les strates.
Les strates et leur contenu sont comme suit en lisant de l'ouest à l'est, dans les moitiés des strates.
2 éléments dans la strate 1 O
8 éléments dans la strate 2 O
18 éléments dans la strate 3 O
32 éléments dans la strate 4 O
32éléments dans la strate 4 E
18 éléments dans la strate 3 E
8 éléments dans la strate 2 E
2 éléments dans la strate 1 E
Total 120 éléments
Si on rassemble les moitiés ouest et est, il y a comme suit dans chaque strate.
4 éléments dans la strate 1 O
16 éléments dans la strate 2 O
36 éléments dans la strate 3 O
64 éléments dans la strate 4 O
Total 120 éléments
Selon n.
À l'intérieur d'une strate, les valeurs de n sont réparties de façon concentrique, avec croissance de la périphérie vers le centre. La plus petite valeur de n se trouve dans les équerres extérieures des quadrants NO et SE. Dans les rectangles de la classification par couches, les valeurs de l croissent plutôt de centre vers la périphérie.
La valeur de n augmente d'une unité lorsqu'on passe d'une équerre NO à l'équerre correspondante NE ou SO, semblablement, lorsqu'on passe d'une équerre SE à l'équerre correspondante SO ou NE. La plus petite valeur de n, soit nmin, qu'on rencontre dans une strate, se lit au coin NO, est comme suit. Elle est égale au numéro d'ordre de la strate.
Strate 1, plus petite valeur de n = 1
Strate 2, plus petite valeur de n = 2
Strate 3, plus petite valeur de n = 3
Strate 4, plus petite valeur de n = 4
Selon n et l. Les sous-couches.
À l'intérieur d'une strate, les équerres c'est-à-dire les demi sous-couches ayant les mêmes valeurs de n et l mais des signes différents sont en regard, c'est-à-dire qu'elle sont situées symétriquement par rapport au centre de l'ellipse. À elles deux, elles composent une sous-couche.
Selon n, l, |m|, les orbitales.
À l'intérieur d'une sous-couche, les cases ayant mêmes valeurs de n, l, |m|, au signe près de m, sont situées en regard et forment ce qu'on appelle une orbitale. L'orbitale et composée de deux cases qui sont ses partenaires. Ainsi Si et Cl.
Orbitales pairées, les tétrades.
À l'intérieur d'une strate, les orbitales se présentent par paires, ayant mêmes valeurs de l et |m| et des valeurs de n égales à une unité près. Les 4 cases soit les 4 éléments concernés forment ce qu'on appelle une tétrade.
Le tableau des 120 éléments est constitué de 30 tétrades.
Le nombre de tétrades dans une strate est égal au nombre de cases dans un quadrant de celle-ci, comme suit.
Strate 1, 1 tétrade
Strate 2, 4 tétrades
Strate 3, 9 tétrades
Strate 4, 16 tétrades
Total 30 tétrades
Les 8 périodes.
Une période représente le contenu de 2 quadrants en regard. Elle est formée d'une suite consécutive de valeurs de Z. Lue par valeurs croissantes de Z, elle se termine sur une case s0+. Il y a 8 périodes, renfermant un nombre de cases soit d'éléments comme suit.
Cette définition de la période diffère de celle de la classification de Mendeleev. Les nouvelles périodes sont tout aussi bien inégales, et la classification n'est pas davantage périodique au sens habituel d'un phénomène périodique en physique : dans un phénomène périodique, les périodes sont égales.
En revanche, les périodes nouvelles se présentent avec une symétrie accrue : 4 groupes appelés strates, de 2 périodes chacune.
Strate 1, période 1, 2 cases
Strate 1, période 2, 2 cases
Strate 2, période 3, 8 cases
Strate 2, période 4, 8 cases
Strate 3, période 5, 18 cases
Strate 3, période 6, 18 cases
Strate 4, période 7, 32 cases
Strate 4, période 8, 32 cases
Total 8 périodes, 120 cases, 120 éléments
Répétons : les périodes dans le tableau de Mendeleev sont définies autrement.
Les 32 groupes d'éléments.
Revenons à la vue en plan de la 2e pyramide. Une case de ce plan soit une colonne de cette pyramide est caractérisée par les même nombres quantiques s, l et m, les nombres quantiques principaux n étant divers. Le même triplet slm se rencontre 2 fois. Un triplet ne contient pas le nombre quantique principal.
Un triplet slm définit un groupe et il y a 32 groupes. Les groupes sont désignés par le nom de l'atome le plus léger qu'ils renferment. Cet atome apparaît aux quadrants NO et SE. Il y a les groupes comme suit. Les numéros des groupes de 1 à 18 sont ceux du tableau de Mendeleev sauf pour l'hélium. Les éléments d’un même groupe sont appelés des congénères.
D'autres classifications renferment 32 cases; celle du Ji-King en renferme le double, soit 64 cases.
Tableau 83. Les groupes des éléments.
...........
Nom du groupe..... Numéro du groupe.......N. d'éléments.....................
Triplet ......Valence, aperçuHydrogène
.........s0.........1.............1...........8Hélium
.............-s0.........2..........0, 2..........8Scandium
.........-d-2........3.............3..........4Titane
..............-d-1.... ...4.............1...........4Vanadium
........-d0.........5.........................4Chrome
............-d1.........6.........................4Manganèse
.......-d2.........7..........................4Fer
...................d-2.........8.............à..........4Cobalt
..............d-1.........9.........................4Nickel
.........,....d0.........10........................4Cuivre
..............d1.........11........................4Zinc
..................d2.........12...........7...........4Bore
.................-p-1......13.............3...........6Carbone
...........-p0........14.............4...........6Azote
...............-p1........15........-3, -5.........6Oxygène
............p-1.......16...........-2......,....6Fluor
.................p0........17...........-1...........6Néon
.................p1........18............0...........6Lanthane
.........-f-3........19............1.....,,,,.2Cérium
.............-f-2.......20.........................2Praséodyme
.....-f-1........21........................2Néodyme
.........-f0.........22........................2Prométhéum
.....-f1.........23........................2Samarium
........-f2.........24........................2Europium
.........-f3..........25........................2Gadolinium
......f-3.........26...........à...........2Terbium
...........f-2..........27........................2Dysprosium
......f-1.........28........................2Holmium
..........f0..........29........................2Erbium
.............f1..........30........................2Thulium
...........f2..........31........................2Ytterbium
.........f3..........32...........7...........2Total
........................................................120 élémentsTableau 84. Les groupes des éléments.
Noms particuliers.
---------------------------------------------
....
Nom .................Numéro ...............Nom particulier....
Hydrogène................1...................Alcalins : z > 1.......
Hélium......................2....................He : Gaz rare...........................................................
et Alcalino-terreux : Z > 2L'hélium a la valence 0 et les alcalino-terreux ont la valence 2.
Scandium
..................3..................Scandides..........Scandium
.................3...................Éléments..........à
........................à....................................Zinc
........................9....}...........{........de............Lanthane
................19.........................................à
........................à.....................................Ytterbium
....................32..................transition.............Fluor
..................17..................Halogènes....Néon
..................18..................Gaz rare.......Fer
............................8........................Mine.........Cobalt
........................9....}...........{........de.............Nickel
......................10..........................fer.............---------------------------------------------
Les éléments Lanthane Z = 57 à Ytterbium Z = 70 sont des Éléments de transition et s'appellent Lanthanides.
Les éléments Actinium Z = 89 à Nobelium Z = 102 sont des Éléments de transition et s'appellent Actinides.
---------------------------------------------
Scandides + Lanthanides + Actinides = Terres rares
---------------------------------------------
Gaz rares : 1 dans le groupe 2, 6 dans le groupe 18.
Le caractère électronique nominal d'un élément. Comment l'obtenir.
Pour tous les éléments de numéro atomique inférieur à 118, on procède par vêlage ou genèse soustractive. Le québécium Z = 118 possède 118 électrons ayant chacun un caractère distinct. Voici une liste partielle de ces électrons et de leurs caractères
Tableau 85. Vêlage du québécium.
Numéro d'ordre de l'électron
.............................................................
Caractère électronique de l'électron118
........+7s0117
........-7s0...
93
........-7f192
........-7f091
........-7f-1...
83
........-6p182
........-6p081
........-6p-1...
14
........-3p013
........-3p-112
........3s011
........-3s0...
3
........-2s02
........1s01
........-1s0Pour obtenir l'atome Z = 92, on enlève tous les électrons depuis le 118e jusqu'au (Z+1)ème = 93e y compris. On conserve les 92 autres. Le caractère du 92e électron est le caractère électronique nominal de l'élément Z = 92, l'uranium. On procède semblablement pour les autres valeurs de Z.
Quant aux atomes Z = 119 et 120, on procède par addition d'un électron -8s0 puis 8s0. Le caractère électronique nominal est celui du dernier électron ajouté.
Ces opérations sont virtuelles.
Tableau demi-elliptique par strates et son doublage. L'antimatière.
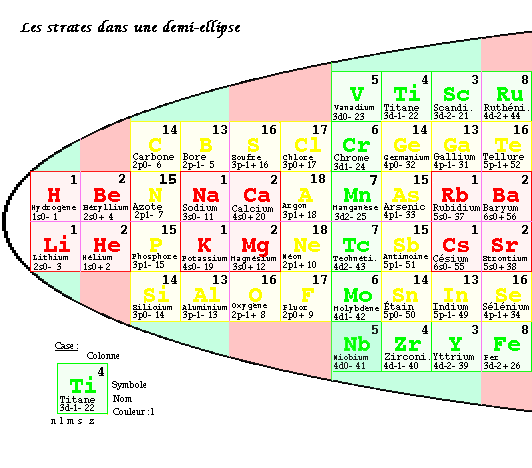

FIG. 8. Les strates dans une demi-ellipse.
Dans le tableau elliptique par strates, les strates 1, 2 et 3 sont divisées, une moitié - à l'ouest, une moitié + à l'est. Ces moitiés peuvent être réunies à l'ouest et le résultat s'inscrit dans une ellipse allongée dont la moitié ouest seule est occupée. C'est le tableau demi-elliptique par strates des atomes de la matière ordinaire. FIG. 8
Cette demi-ellipse est uniquement définie. Demi petit-axe 4,33, demi grand-axe 20,66, l'unité étant le côté d'une case, rapport 0,210 = 1/4,77
Les signes se présentent en alternance dans les moitiés ouest et est de chaque strate.
La demi-ellipse non occupée à l'est n'est pas purement imaginaire. On peut y placer un tableau symétrique par rapport au tableau ouest, qui représenterait les atomes des antiéléments de l'antimatière. Jusqu'ici, on a réussi à réaliser des atomes d'antihydrogène, composés d'un antiproton ou proton négatif et d'un antiélectron ou positon. P pour proton.
antiH = (P- e+)
Cet antiatome isolé est stable. Il disparaît lorsqu'il touche des composantes de la matière ordinaire. Cela se fait par une double réaction : nucléaire entre P- et P+, électronique entre e+ et e-. Référence CERN 2002. FIG. 9
http://livefromcern.web.cern.ch/livefromcern/antimatter/FRENCH/factory/F-factory04.html
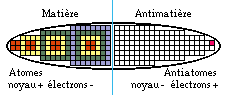
FIG. 9. Classification elliptique des atomes et des antiatomes. Le seul antiatome réalisé est l'anti-hydrogène.