Système du Québécium.

Pierre Demers 2013. Système du Québécium.

Fonction Implication

Système du Québécium.*

Nécessité d’une fonction

I

implication, observateur intelligent

existant

de toute éternité.

Pierre Demers

Traduction interdite.

1erV2013, 21V2013, 28V2013.

Sommaire. J’ai écrit précédemment que 30 implique nécessairement 4,

que 30 étant présent de toute éternité dans l’espace-temps, il se trouve

nécessairement accompagné de 4, donc également de toute éternité. Ce qui

suggère que le système mathématique du québécium a toujours existé, avec

pour conséquence d’offrir un plan pour l’organisation des atomes inertes

(l’alpha) et celle de l’être humain (l’oméga). Je crois opportun de

revenir sur ces considérations abstraites, afin de les formuler dans le

vocabulaire du fondement des mathématiques. J’en arrive à la conclusion

que l’espace-temps à lui seul est dénué de tout pouvoir de planification ou d’organisation

de quoi que ce soit, choses nécessaires pour qu’il y ait création pour utiliser ce terme du langage

commun. Et que l’intervention d’un observateur intelligent au sens du

langage commun encore une fois, est indispensable pour comprendre que

l’Univers existe. Son existence anticipe la création de la matière. Cette intervention peut s’exprimer comme une fonction

agissant sur les nombres, et se figurer par un I majuscule, qu’on pourra

lire comme implication, intelligence, inventivité. Pour mieux le

différencier du i minuscule signifiant imaginaire racine carrée de -1 ou

autre chose, on l’écrira de préférence avec un point le chapeautant,

donc dans une fonte appropriée que je n’ai pas encore identifiée. Cette

fonction, dans son application la plus élémentaire, associe 30 à la

symétrie 4, puis au nombre 120, etc, par des raisonnements par exemple sur des sphères assemblées. Dans ses formes les plus

développées, elle fait apparaître, à la limite, l’ensemble des

mathématiques connues et restant à connaître.

Einstein, Poincaré.

Les fondateurs de la doctrine de la relativité restreinte ont argumenté,

vers le début du 20^e siècle , avec le succès que l’on sait, en faisant

intervenir un observateur apte à reconnaître des signaux optiques et à

lire des horloges. Depuis cette époque, toute discussion fondamentale

sur l’univers doit se placer dans le cadre de l’espace-temps. On peut

soutenir que cet observateur est doué de certains aspects de la fonction I.

Pythagore. Démocrite. Platon.

L’École Pythagoricienne, qui a duré de -640 à -480 approximativement. « Tout dans le monde est nombre » était la base principale de leurs spéculations, s’accordant avec l’affirmation de Démocrite (-480-), que

tout dans le monde est composé de grains discrets, donc dénombrables.

Réf. 1. Platon, Léon Robin, Antoine Danchin.

Platon, génie universel (vers -428 - vers -348), ami de Socrate qui ne

laissa aucun écrit, et d’Aristote, apporta la notion des idées, qui

nous intéresse. Telle l’idée d’un cube ou d’une sphère, disait-il.

Prenons une collection de dés cubiques ou de boules sphériques.

Ils peuvent être grands ou petits, d’une matière ou d’une autre.

Nous les appelons tous du même mot, soit cube, soit sphère. Il y a donc quelque part l’idée

d’un cube et celle d’une sphère, qui est

immatérielle et impalpable, pouvant être figurée dans une multitude

d’objets qui la concrétisent. Mais les idées elles-mêmes se trouvent

dans un monde intelligible, distinct du monde des sens. Réf. 2.

Yvon Gauthier.

Je trouve beaucoup qui touche le sujet proposé, dans son livre

/Fondements des mathématiques. Introduction à une philosophie

constructiviste/. Constructivisme veut dire à peu près, que c’est en

expérimentant qu’on devient expérimentateur, ou, en espagnol :

Camminando se hace el cammino , ou en latin : Fabricando fit

faber. Je refais sa figure unique, de la couverture et page 20.

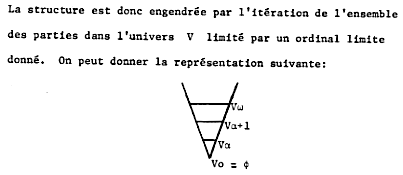
Figs 1 et 2. Figure, couverture et page 20 de Fondement des

mathématiques par Yvon Gauthier. Réf. 3.

Dans cette figure bidimensionnelle, l’ordinal limite est le 3e,

apparaissant par une ligne. Je passe à l’ordinal 4e , par l’inscription

d’une ligne supplémentaire à un niveau supérieur, puis je remplace les

longueurs 1, 2, 3, 4 par des boules en nombres correspondants, puis je

passe à une structure tridimensionnelle, qui est celle d’une pyramide de

30 boules. C’est l’équivalent, le bas en haut, de Fig. 3.

Fig. 3. Réf. 4. Fonction I : l’observateur peut raisonner sur des sphères immatérielles égales.

Piaget.

L’observateur intelligent que j’invoque, avec sa fonction I ressemble

beaucoup, dans sa forme la plus rudimentaire au jeune enfant de Piaget,

qui apprend à jouer avec les nombres. Thérèse Gouin-Décarie a étudié

avec Piaget.

À compléter.

Thérèse Gouin-Décarie, Jean-Luc Gouin, Aubert Daigneault et Yvon

Gauthier voudraient-ils commenter? Réf. 5.

Références.

Réf. 1. Cyberscol,

http://www.ac-orleans-tours.fr/hist-geo-grece/themes/philo.htm

http://fr.wikipedia.org/wiki/Pr%C3%A9socratiques#TableauéchronologiqueédeséprincipauxéPr.C3.A9socratiques,

http://mendeleiev.cyberscol.qc.ca/carrefour/rescol99/atome-1.html

Réf. 2. Léon Robin, Platon, Alcan 1938, http://digression.forum-actif.net/t55-platon-theorie-des-idees

Antoine Danchin

Est-ce celui-ci : ENS 1964 s a.danchin@amabiotics.com, http://www.normalsup.org/-adanchin/ ?

Réf. 3. Yvon Gauthier 1976, /Fondements des mathématiques. Introduction

à une philosophie constructiviste, Montréal, PUM (Presses de

l’Université de Montréal), 1976, 460 pages.

Réf. 4. Pierre Demers 2013 Québécium,

http://www.lisulf.quebec/quebecium.htm

Réf. 5. Jean-Luc Gouin, Aubert Daigneault et Yvon Gauthier,

LePeregrin@yahoo.ca,

daigneau@dms.umontreal.ca, gauthier@DMS.UMontreal.CA

- 30 -

* *