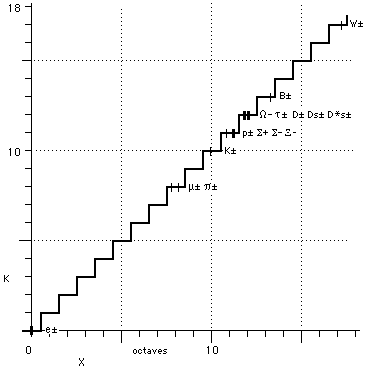
Fréquences de de Broglie pour la matière électrique
Pierre Demers
Centre québécois de la Couleur
1200, rue Latour, Saint-Laurent (Québec) H4L 4S4
Soumis aux Annales de la fondation Louis de Broglie, septembre 1991.
Refusé
RÉSUMÉ. Nous examinons les rapports des fréquences associées aux particules élémentaires selon l'équation donnée par de Broglie en 1923. Un modèle biomathématique suggère que ces rapports pourraient être ceux de l'octave et de la gamme tempérée en musique. La matière obéirait alors à un modèle musical que nous présentons. Les particules chargées les plus fondamentales s'accordent particulièrement bien avec ce modèle, manifestant des règles de quantification basées sur un nombre quantique nouveau attribué à la matière électrique, que nous appelons isogamme. Cet accord jette un jour nouveau sur la nature de l'électricité et suggère que toute masse pourrait être d'origine électromagnétique. Le modèle musical suggère une prédiction concernant les masses de particules très lourdes non encore observées (particules de Higgs) : elles se situeraient au voisinage de m
I. Introduction
Ondes associées. La justesse des vues que Louis de Broglie émettait en 1923, en affirmant le caractère ondulatoire de la matière en mouvement, n'est plus à démontrer. Encore récemment, on lui a trouvé une confirmation ou une application, en observant les interférences des faisceaux de neutrons et d'atomes, permettant de mesurer la longueur de l'onde associée à de telles particules en mouvement.[1][2]
Vibrations associées. La fréquence de de Broglie. L'équation originale que de Broglie écrivit en 1923 concernait le caractère vibratoire d'une particule au repos et attribuait à une telle particule une fréquence propre, que nous appellerons fréquence de de Broglie. La masse au repos étant mo.[3]
f = m
oc2/h (1)Si on écrit la masse m en Mev, voici la formule donnant la fréquence en Hertz. Nous l'écrivons avec les valeurs tirées des tables récentes.
f = 0,409.62 m 269 (2)
Cette fréquence intervient par un facteur e2πift chaque fois que l'on écrit la fonction Y dépendante du temps.
Un photon d'énergie E possède une fréquence f = E/h et une longueur d'onde qui sont observables. En revanche, la fréquence de de Broglie d'une particule au repos est loin de se manifester de façon aussi évidente que la longueur d'onde de la même particule en mouvement. En effet, sa probabilité de présence dans un état stationnaire n'est nullement vibratoire. Elle s'obtient en prenant le carré de Y ou produit Y Y*, renfermant les facteurs e2πift et e-2πift, dont l produit est une constante. Consécutivement, cette fréquence est une quantité "évanescente" lorsqu'on cherche à l'observer directement. Elle paraît dépourvue de réalité physique et valable uniquement comme un algorithme ou un artifice mathématique commode.
Par la suite, les auteurs ont rarement discuté de ces vibrations. de Broglie lui-même ne semble pas s'être arrêté à discuter de leurs valeurs. de Broglie et les autres auteurs ont popularisé l'appellation mécanique ondulatoire et non mécanique vibratoire. Utilisant l'adjectif "ondulatoire" alors qu'ils pourraient employer "vibratoire", ils s'attachent aux ondes et non aux vibrations. On trouve des exemples de telle réserve chez Hurwic, Daviau et Messiah.[4][5][6] En revanche, Hoffmann et Paty insistent sur les vibrations, et, dans un livre qui rapproche orientalisme et physique, Capra parle des danses et des chansons des atomes et des fréquences des particules.[7][8] L'onde associée à la fréquence d'une particule au repos est une onde stationnaire, elle ne peut pas être une onde émise. Schrödinger parla de ces fréquences. Il fit le calcul et trouva 0,227 billions de billions de Hz pour le proton (0,227 TTHz ou 2,27 1023 Hz, ou encore 384,3 269 Hz).[9]
Notre échantillon. Nous appliquerons notre modèle aux particules élémentaires chargées, restreignant notre investigation à un échantillon de ces particules dont la présente étude suggère qu'elles sont plus vraiment élémentaires que les autres. En effet, on connaît près de 100 particules chargées subatomiques que l'on appelle élémentaires dans un sens large. L'échantillon que nous retenons présentement renferme 15 particules que nous appellerons dès maintenant "fondamentales" (Tableau I).
Tableau I. Notre échantillon de 15 particules chargées fondamentales.
M masse, l'unité étant celle de l'électron 0,511 Mev.
3 leptons électron e± (1)
muon µ± (206,77)
tau t± (3491,4)
1 boson de jauge
W± (157730)
11 hadrons
6 mésons
kaon K± (966,05)
pion π± (273,13)
D± (3658,1)
D*± (3582,8)
D*s± (4129,7)
beauté B± (10328)
5 baryons
proton p± (1836,15)
sigma S + (2327,5)
sigma S - (2342,3)
xi X- (2385,8)
oméga W - (3272,9)
Cette liste est une partie de celle des 19 particules chargées appelées "stables" et désignées par la lettre S dans les tables reconnues.[13] En fait, seuls le proton et l'électron sont apparemment stables, mais les 17 autres particules sont stables vis-à-vis de la désintégration par interactions fortes et ont des périodes comparativement plus longues que les autres. Parmi ces 19 particules S, on range 4 baryons charmés : Lc+ (4472), S ·c++ (4800,4), X c+(4800,8), Xc+ (4827,4). Nous avons trouvé nécessaire d'exclure ces derniers par une analyse interne décrite plus loin. De la sorte, notre échantillon consiste en 15 particules S. On compte une fois seulement deux particules semblables de même masse connues sous le signe + et le signe -. Les masses du Tableau I sont tirées des tables de 1990.[14] Leur précision est meilleure que ±0,2 % sauf le W± (±0,5 %).
II. Un modèle musical
Rapports de masses. Alors qu'au moment où de Broglie écrivait sa formule originale, on ne connaissait que le proton et l'électron, on connaît maintenant un grand nombre de particules subatomiques ou élémentaires et on possède des listes de leurs masses. Arrêtons-nous à considérer les rapports de ces masses comme étant les rapports de leurs fréquences de de Broglie. S'il est vrai que les fréquences des particules sont inobservables, les rapports de leurs fréquences sont parfaitement accessibles. On peut songer à établir un parallèle avec une autre collection de fréquences et de rapports de fréquences, celle des sons musicaux.
Parallèle biomathématique. L'humanité, ayant acquis une longue expérience des fréquences audibles formant son ambiance sonore, a abouti à la nécessité d'organiser leurs périodicités selon des règles mathématiques appelées musicales. Cette organisation remonte à Pythagore, découvrant que la musique est nombre. De ces règles musicales, qui apparaissent comme une conséquence fondamentale de la nature humaine, nous retenons principalement le facteur 2 déterminant la périodicité d'octave et la division de l'octave en douze demi-tons égaux, appelés demi-tons diatoniques, formant la gamme tempérée. Nous appellerons degré diatonique ce demi-ton diatonique, égal à un facteur b = 21/12. = 1,059.463. Nous faisons l'hypothèse d'un parallèle, à ce propos, entre la nature humaine et la nature inanimée. Il n'est pas interdit de supposer que la nature inanimée elle-aussi imposerait des règles comparables aux fréquences inaudibles des particules constitutives de l'univers. Nous proposons que les masses des particules élémentaires répondraient aux rapports musicaux tels que ceux de la gamme tempérée et de l'octave, selon une règle de gamme et une règle d'octave, respectivement. Ce rapprochement a été inspiré par des motifs philosophiques et esthétiques. Tel est notre modèle musical, qui continue les "Lois du spectre de masse des particules" de Joël Sternheimer.[12][13][14]
Les hauteurs. Aussi bien qu'en musique, il faudra nous attacher aux hauteurs, logarithmes des rapports de fréquences, c'est-à-dire aux logarithmes des valeurs de M. Nous utiliserons, pour ces logarithmes, tantôt la base 2 et tantôt la base b.
Aspects innovateurs. Dans le contexte de la physique contemporaine, notre démarche est une innovation qui peut surprendre à cause des différences méthodologiques habituelles entre la biologie et la physique. Elle a peu de chose en commun avec les démarches en cours basées sur le modèle standard des particules élémentaires, lequel a conduit au modèle des cordes et des supercordes.
1. Rapprochements biologiques. La biophysique contemporaine cherche à expliquer la biologie par la physique plutôt que la physique par la biologie. Pourtant, la théorie des ondes stationnaires, essentielle en musique, a servi dans l'élaboration de la mécanique ondulatoire. Plus récemment, un parallèle avec les mathématiques de la perception colorée a servi de point de départ à la chromodynamique quantique, partie essentielle du modèle standard, modèle confirmé jusqu'ici "d'une façon éclatante", selon Rubbia.[15]
Certains travaux récents cherchent à résoudre la disjonction entre biologie et physique. On peut les faire remonter à Louis Pasteur et ils s'attachent aux phénomènes de chiralité, qui mettent en évidence des dissymétries gauche-droite. Voyez Laforgue.[16] Du reste, on pourrait aussi bien créer le modèle musical défini ci-dessus sur une base purement heuristique sans l'appeler musical, et conclure à un rapprochement avec la biologie.
2. Analyse de données. Étant fondés sur les nombres magiques 2 et 12, la musique et notre modèle musical sont des numérologies, bien différentes de celles des occultistes. D'autres analyses numériques ont fait avancer notre connaissance quantifiée de la matière. Ainsi Balmer introduisit des nombres entiers par l'analyse harmonique de 4 nombres tirés du spectre de l'atome d'hydrogène. Ces nombres entiers sont devenus des nombres quantiques dans la mécanique ondulatoire.
[17] Ainsi Béguyer de Chancourtois et Goeppert-Mayer découvrirent, l'un la classification périodique des éléments et l'autre, le modèle en couches du noyau.3. Le modèle standard des particules élémentaires nous sert dans la définition d'un échantillon de particules que nous soumettons à l'analyse. Il jouit d'une vogue considérable et il sert de base à la quasi-totalité des publications dans ce domaine. Malgré le grand nombre de ces publications, il est fascinant de reconnaître que ce modèle comporte des lacunes, d'après ce qu'on trouve écrit en 1990 au sujet de l'accélérateur d'électrons LEP du CERN, Organisation européenne pour la physique des particules.
Les résultats obtenus au LEP jusqu'ici ont confirmé le "modèle standard" d'une façon éclatante. Un aspect fascinant de ces travaux est que nous savons que ce modèle ne peut pas livrer la clé complète de l'interprétation de la nature : il comporte des lacunes, ce qui signifie forcément qu'il y a une nouvelle physique à découvrir. Rubbia [15]
Notre modèle musical pourrait aider à combler ces lacunes. Nous procédons à l'application des règles de notre modèle à notre échantillon.
Application à notre échantillon. Nous analysons les hauteurs relatives à notre échantillon. Voici les fonctions dont nous avons besoin. M est la masse tirée du Tableau I. Remarquez K, H, D. (Figs 1 à 7)
hauteur en octaves
X = log
2M (3)hauteur en octaves arrondie à l'entier le plus proche ou N
o d'octave KX = ent(X+0,5) (4)
différence de hauteur en octaves
D
X = X-X (5)hauteur en degrés diatoniques
x = logbM = 12X (6)
hauteur en degrés diatoniques arrondie à l'entier le plus proche
x = ent(x+0,5) (7)
différence de hauteur en degrés diatoniques ou dissonance D
D
x = x-x (8)hauteur dans la gamme en degrés diatoniques
h = x-12X (9)
hauteur dans la gamme arrondie à l'entier le plus proche en degrés diatoniques
ou N
o de gamme Hh = ent(h+0,5) (10)

Figure 1. Numéro d'octave K pour les particules de notre échantillon, fonction discontinue de X.
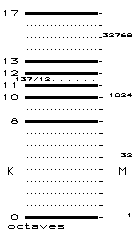
Figure 2. Numéros d'octave K pour les particules de notre échantillon dans un diagramme par niveaux
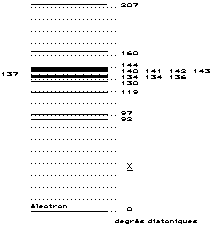
Figure 3. Règle d'octave pour les particules de notre échantillon. Diagramme par niveaux x. Les pointillés sont espacés de 12 unités.
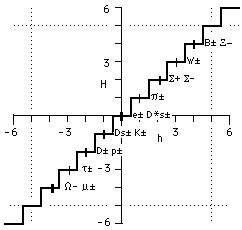
Figure 4. Numéro de gamme H pour les particules de notre échantillon, fonction discontinue de h.
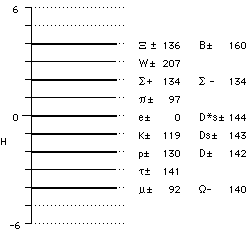
Figure 5. Règle de gamme. Les N
os de gamme H pour les particules de notre échantillon dans un diagramme par niveaux. 9 valeurs sont réalisées sur 12 possibles. On a marqué les valeurs de x.
Figure 6. Règle de gamme. La hauteur H réalise 9 notes, de fa à do#, autour du la 428,7 Hz (au lieu de 440 Hz).
1. Règle d'octave. Notre règle d'octave s'énonce ainsi : "Les masses M se présentent selon une progression géométrique de raison 2". Les valeurs de X se situeraient aux hauteurs X = 0, 1, 2, 3, 4, etc. Cette règle ne s'accorde pas avec les valeurs individuelles des masses. Les valeurs réalisées de K sont comme suit.
0, 8, 10, 11, 12, 13, 17
Leur somme pour les particules plus lourdes que l'électron, pondérée par le nombre de ces particules, est 160. Leur moyenne multipliée par 12 est 137,14, valeur remarquablement proche de l'inverse de la constante de structure fine 1/
a = 137,04. Toute somme autre que 160 donnerait une moyenne s'écartant davantage de 137,04/12.Les valeurs de
DX restent comprises par construction entre -0,5 et +0,5 et, selon l'expérience, entre des limites plus resserrées : -0,323 et +0,337. La règle d'octave représente les masses individuelles avec un écart d'un facteur restant compris entre 1/1,251 et 1,263. Elle exprime une tendance des valeurs expérimentales à se grouper autour de certains degrés exacts de cette échelle et à éviter le milieu entre ces degrés.De plus, on trouve que la moyenne de
DX pour les particules plus lourdes que l'électron est sensiblement nulle : elle vaut 0,005. Pour l'échantillon de notre choix, la règle d'octave s'accorde remarquablement bien avec la moyenne des hauteurs expérimentales.2. Règle de gamme. Notre règle de gamme peut s'énoncer ainsi : "Les hauteurs h ont des valeurs entières H."
Ces hauteurs correspondent à des fréquences réduites par transposition à une octave unique, centrée sur la fréquence de l'électron elle même réduite au voisinage du la normal 440 Hz par transposition de 58 octaves. Cette fréquence réduite de l'électron est 428,7 Hz. Supposons pour un instant que les fréquences réduites des 15 particules appartiendraient toutes exactement à une gamme tempérée avec la = 428,7 Hz. Alors les 15 hauteurs seraient des nombres entiers. C'est ce que signifie la règle de gamme.
Les N
os de gamme H réalisés sont -4, -3, -2, -1, 0, 1, 2, 3, 4. Les Nos -6 ou 6, -5 et 5 sont absents. (Fig. 5) Chacun de ces Nos peut porter un nom de note et désigne un domaine de hauteurs h de H-0,5 et H+0,5. L'électron étant un la, il est entouré symétriquement du sol# à gauche et du la# à droite, etc. Les noms de notes réalisés vont du fa au la et du la au do#. Le ré, le ré# et le mi sont absents. La figure 6 présente ces notes sur une portée musicale.Les valeurs de h apparaissent à la figure 7, où les coordonnées circulaires font ressortir le caractère cyclique de notre analyse. La numérotation en 12 degrés diatoniques, à la manière des 12 heures d'un cadran d'horloge, présente un avantage sur la désignation par des noms de notes parce qu'elle est en chiffres et continue entre les entiers.
La figure 7 montre des régularités remarquables, réclamant plus ample analyse. Les hauteurs expérimentales h ne s'accordent pas avec la règle de gamme. Elles se placent au voisinage des valeurs exactes H requises par cette règle, avec un écart que nous appelons dissonance D.
D = h-H (11)
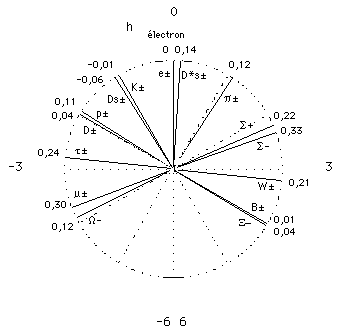
Figure 7. Règle de gamme. Diagramme circulaire des hauteurs h, montrant des régularités remarquables. On a marqué la dissonance D.
Résumons nos résultats. Les masses répondent à une équation renfermant trois facteurs d'importances inégales : 1º celui de la règle d'octave avec K; 2º celui de la règle de gamme avec H; 2º un facteur dépendant de D.
Formule de masse musicale M = 2
KbHbD = b12K+H+D (12)3. Contrôle des régularités. L'apparence de régularités de période unité, dans la figure 7, peut se confirmer par une analyse statistique telle que celle-ci. On prend la différence ∂ h entre chacune des 15 valeurs de h et les 14 autres. En évitant les duplications, on trouve 105 différences absolues distinctes. La distribution de ces valeurs modulo 1 apparaît à la figure 8 de Elles montrent un maximum marqué au voisinage de 0 ou 1. La périodicité apparente de période 1 h. s'en trouve confirmée objectivement. Puisque la fonction modulo 1 fait disparaître la partie entière de l'argument, on obtient le même résultat en prenant ∂ x.
4. Dissonances. Les dissonances, qu'on peut lire sur la figure 7, ne sont pas nulles, sauf pour l'électron, et elles sont pour la plupart positives, restant comprises entre -0,06 et 0,33. Leur moyenne algébrique est 0,116.
D
moyalg = 0,116 (13)Le terme b
D vaut en moyenne algébrique 1+0,70 %. Si l'on considère les dissonances comme des écarts par rapport à la règle de gamme, l'écart moyen algébrique vaut +0,70 % sur les masses. Cet écart dépasse les erreurs dans la mesure de la plupart des masses, inférieures à 0,1 % sauf pour t± (±0,17 %) et W± (±0,5 %). Les valeurs de D sont pour la plupart positives et leur moyenne arithmétique vaut 0,13. Il s'ensuit un écart arithmétique moyen +0,76 % sur les masses.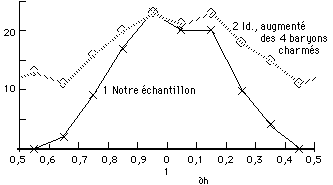
Fig. 8. Distances mutuelles entre les hauteurs. Diagramme 1. Analyse statistique interne des distances ∂h entre les hauteurs h pour les particules de notre échantillon (fig. 6). La distribution est resserrée autour de ∂h = 0 ou 1. Diagramme 2. Même analyse en incluant les baryons charmés (fig. 11). La distribution est élargie.
Puisque les valeurs de D sont pour la plupart positives, il est facile de réduire leur moyenne arithmétique en déplaçant l'origine des Nos de gamme dans la figure 7 vers les valeurs positives. En la déplaçant de 0,11 degrés diatoniques, on trouve l'écart arithmétique moyen suivant. Cela revient à examiner le rapport des masses m/m', y compris la masse de l'électron, par rapport à une masse fictive m' supérieure de 0,64 % à celle de l'électron. (m/m' au lieu de m/me±).
s
arith = 0,55 % (14)En considérant les dissonances comme des écarts,
sarith donne une mesure de l'accord entre les masses expérimentales et notre modèle musical.5. Analyse des dissonances. La présence de dissonances D non nulles peut s'interpréter par l'intervention de gammes connues en musique, utilisant des rapports numériques autres que ceux de la gamme tempérée. Joël Sternheimer a analysé les dissonances pour 38 particules et a reconnu qu'elles forment 6 classes qu'il a nommées A, B, C, D, E, F, qu'il explique par une synthèse des gammes d'Orient et d'Occident.[10][11] Longavesne et Demers ont confirmé ses résultats.[24][25] Les particules de notre échantillon se rangent dans les classes D, E et F. Nous avons remarqué, dans un travail inédit, que les dissonances sont de préférence positives pour les particules chargées, tandis qu'elles sont de préférence négatives pour les particules neutres.
Valeur précise de 2. On peut se demander si la valeur précise de 2 est requise dans les équations. En remplaçant 2 par 2(1±1%), nous avons vérifié que toute apparence de régularité disparaît dans la figure 6. Une manière plus rigoureuse de contrôler si la valeur précise de 2 est requise consiste à remplacer 2 par 2(1+
e) et à chercher si une valeur de e différente de zéro peut réduire l'écart arithmétique sarith trouvé ci-dessus égal à 0,55 % On obtient le minimum de sarith pour e = -0,0007, c'est-à-dire que la valeur précise de 2 devrait être remplacée par 1,9986, ou encore, qu'elle est confirmée à 0,07 % près. La valeur minimale de sarith est comme suit.s
arith = 0,54 % (15)Il faudra refaire ce calcul lorsque les masses seront connues avec une meilleure précision, en particulier celles du
t± et du W± .Cette confirmation de l'intervention du nombre exact 2 est satisfaisante au point de vue de l'analogie musicale fondant notre modèle et aussi parce que notre modèle concerne la matière électrique, alors que la valeur précise du nombre 2 intervient en électromagnétisme.
Résonances et répulsions. Les propriétés des oscillateurs couplés en mécanique classique pourraient expliquer l'absence de coïncidences exactes entre h et H. Le couplage de 2 oscillateurs de fréquences voisines peut accroître la différence de leurs fréquences au lieu de les amener à l'unisson. Telle propriété devrait évidemment intervenir dans une théorie musicale complète. L'analyse que voilà suggère que les masses de la matière électrique pourraient se comprendre comme un système d'oscillateurs tous en interaction mutuelle.
III. Quelques symétries
La physique contemporaine a progressé par la reconnaissance et l'analyse de symétries et de conservations. Examinons donc les symétries que manifeste l'application de la règle de gamme. (Fig. 7)
Centrage sur l'électron. Il est satisfaisant que l'électron, particule de matière électrique considérée comme fondamentale s'il en est, occupe une position centrale. Ce centrage peut s'évaluer de diverses manières.
1. Sept valeurs de h sont négatives et autant sont positives.
2. Pour les 15 valeurs de H, en comptant une fois chacune des positions horaires occupées, la somme est nulle.
S
H = 0 (16)Diverses sommes et moyennes sont intéressantes, concernant h, H et D. Si le centrage était exact, dans chaque cas, la somme et la moyenne seraient nulles et le facteur sur la masse serait égal à 1.
3. Pour les 15 valeurs de H en les comptant une fois pour chacune des 15 particules.
S
-1moy. -0,067
facteur sur la masse 1-0,388%
4. Pour les 15 valeurs de D.
S
1,81moy. 0,121
facteur sur la masse 1+0,701%
5. Pour les 15 valeurs de h.
S
0,81moy. 0,054
facteur sur la masse 1+0,312%
On voit que H et D ont des effets opposés, qui se compensent partiellement dans leur résultante expérimentale h.
6. Appelons multiplicité
M le nombre de particules figurant à un Nº de gamme déterminé entre H = -4 et +4. M prend les valeurs 1 ou 2 et la succession de ces valeurs est comme suit, de gauche à droite.M
:2, 1, 2, 2, 2, 1, 2, 1, 2 (17)
Si l'on additionne les multiplicités rencontrées aux divers Nos de gamme H non nuls, en les affectant du signe - si H est négatif et du signe + si H est positif, la somme est -1.
S
M = -1 (18)
Nonet. Les 9 Nos de gamme mis en évidence forment un nonet.
1. Déterminisme. Si la distribution des fréquences était aléatoire à travers l'octave, on n'aurait aucune raison de s'attendre au vide observé aux degrés 5, 6 et 7 et au remplissage exclusif de 9 positions horaires consécutives. Cela nous suggère de formaliser le fait de l'occupation exclusive de ces 9 positions et de déclarer que nous avons affaire à un nonet chargé de signification physique.
Cette vue se trouve confirmée objectivement par une démarche probabiliste. Supposons d'abord 15 boules identiques à répartir de façon aléatoire entre 12 boîtes égales consécutives ordonnées. Combien y-a-t-il de configurations? La réponse est la cardinalité de l'ensemble universel : 7.726.160. Supposons maintenant que les trois premières boîtes soient vides et que les 15 boules occupent chacune des 9 boîtes suivantes. Alors il est nécessaire que 6 boîtes renferment chacune 2 boules et que 3 boîtes en renferment chacune une. Le nombre de configurations est 84. D'après cela, la chance que le hasard conduise les 15 particules à éviter les positions horaires 5, 6 et 7 et à se répartir de manière que les 9 autres positions soient toutes occupées est 84/7.726.160. En d'autres termes, la chance que l'apparition du nonet observé soit due au hasard vaut tout au plus
84/7.726.160 = 0,000.1 %. (19)
2. Clôture. Nous raisonnons en supposant expressément que la liste des particules composant notre échantillon soit close. Raisonner sur des absences n'est pas sans risque. Cependant il y a des raisons de croire qu'effectivement la liste de ces particules soit close, puisque, malgré des recherches intensives, on n'a trouvé aucune particule nouvelle entrant dans notre échantillon depuis 1983. S'il est vraisemblable que d'autres particules soient encore découvertes, grâce à des accélérateurs plus puissants, elles seront probablement pour la plupart des états excités de celles que l'on connaît et ne seront pas de notre échantillon. Inversement, la cohérence des symétries rencontrées dans le nonet suggère qu'il se suffit à lui-même et on peut en tirer un argument pour déclarer que la liste mentionnée est close.
3. Occupation. Chacun des Nos de gamme du nonet centré sur l'électron est occupé par au moins une particule.
4. Exclusion I. L'absence de multiplicités autres que 1 et 2 peut s'exprimer dans les termes d'un principe d'exclusion, comme suit. "Dans le nonet, un N
o de gamme ne peut pas être occupée par plus de deux particules". La présence d'une troisième est exclue.5. Exclusion II. Le principe d'exclusion paraît être plus exigeant pour les deux particules jouant un rôle d'échange bien connu, le pion
p ± et le boson de jauge W±. Le pion est isolé à sa position horaire, et il en est de même pour le boson de jauge. "Dans le nonet, un No de gamme portant une particule d'échange ne peut porter une autre particule".Transitions. Les transitions respectent des règles de sélection.
1. Produit immédiat. Lorsqu'il y a désintégration d'une particule du nonet ocupant une position H1, un produit immédiat de la désintégration est une autre particule du nonet occupant une position H2. Alors H varie nécessairement d'un nombre entier DH = H2-H1 compris entre 0 et 8. DH est rarement nul. Il est nul pour Ds± donnant K±.
|
DH| = 1 à 8 DH _ 0(sauf Ds±
fi K±) (20)Cette règle ressemble à celle concernant le quantum principal n lors de l'émission d'une raie de l'atome d'hydrogène :
Dn est un entier mais n'est pas nul.DH est de signe opposé à H1 pour H1 > 0. À cet égard, D*s± se comporte comme ayant H1 > 0. Cela peut s'exprimer par le signe du quotient DH/H1.
D
H/H1 < 0H > 0 (21)
Pour H
1< 0, le quotient DH/H1 est négatif, nul ou positif.2. Produit terminal. La désintégration mentionnée ne peut qu'aboutir finalement, au besoin à la suite d'une chaîne, à une particule stable occupant la position Ht, électron ou proton, Appelons DHt = Ht - H1 la variation finale de H. On trouve alors que, dans tous les cas, DHt et H1 sont de signes opposés.
D
Ht/H1 < 0 (22)IV. Formalisme isogamme
Vecteur isogamme. La considération du nonet que nous venons de décrire suggère une formalisation quantique, dans laquelle nous imaginons un vecteur 9 fois dégénéré, à la manière d'un isospin qui vaudrait 4, ayant 2X4 + 1 = 9 projections. Nous l'appellerons isogamme H. H = 4, ses projections dans un espace abstrait sont H, elles sont au nombre de 9 et elles lèvent la dégénérescence d'ordre 9 qui existerait autrement. Ses projections vont de -4 à +4. On peut concevoir H comme un vecteur dans un espace abstrait appartenant à la matière électrique.
projections de l'isogamme H = H = -4, -3, -2, -1, 0, 1, 2, 3, 4 (23)
Dans l'effet Zeeman et dans le cas de l'isospin imaginé par Heisenberg, un vecteur entier ou semi-entier admet des projections quantifiées sur un champ levant la dégénérescence qui existerait autrement. Pour l'effet Zeeman, le champ déterminant est magnétique, pour l'isospin, le champ déterminant est abstrait. Dans l'effet Lo Surdo-Stark, il se passe quelque chose d'analogue sous l'influence d'un champ électrique. Les niveaux apparus par l'effet Zeeman normal sont uniformément espacés sur une échelle linéaire des énergies. Ici l'espacement est uniforme sur une autre échelle : sur une échelle logarithmique formalisée des énergies ou de la gamme musicale.
Le numéro d'octave K apparaît comme un nombre quantique déterminant des niveaux munis d'une dégénérescence que lève l'intervention des projections de H. Nous déclarons que les masses dégénérées répondent à la liste suivante, liste de masses octaves, chaque valeur étant à l'octave supérieure de la précédente. L'unité est la masse de l'électron.
1, 2, 4, 8, 16, ..., 1.024, ...., 1.048.576, (24)
Les valeurs de K sont les numéros de ces octaves en commençant par zéro.
K = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 (25)
Les 7 valeurs réalisées sont soulignées. Il y a ainsi 7 octaves à envisager (aussi bien qu'il y a 7 périodes et 7 valeurs de n, quantum principal, dans le tableau périodique bien connu des éléments).
K = 0 8 10 11 12 13 17
(26)Ces masses octaves sont dégénérées et l'ordre de cette dégénérescence vaut 9 pour toutes les octaves. La levée de la dégénérescence introduit, entre la masse octave et la masse réalisée, un facteur compris entre 1/1,251 et 1,263.
Remplissage des octaves. Nous procédons au remplissage de 7 octaves successives, aussi bien que, pour expliquer la structure électronique des éléments, on procède au remplissage de 7 périodes successives, avec n = 1, 2, 3 ... Le numéro d'octave K détermine ainsi le niveau énergétique dans sa partie principale. La hauteur H joue ensuite, un rôle analogue à
Ayant quitté l'octave K = 0 (H = 0) où l'électron est isolé, on remplit 2 sous-niveaux de l'octave K = 8 avec le muon et le pion (H = -4 et 1). Puis on trouve le kaon, seul dans l'octave K = 10 (H = -1). On note le remplissage spécialement intensif des niveaux 11 (H = -2, 2, 2, 4) et 12 (H = -4, -3, -2, -1, 0), renfermant un lepton, des mésons et des baryons. Ce dernier remplissage affecte 7 sous-niveaux sur les 9 possibles. L'octave K = 13 renferme exclusivement le méson B± (H = 4) et l'octave K = 17, exclusivement le boson de jauge (H = 3).
En définitive chaque valeur possible de H est réalisée, soit une fois soit deux fois. Si une valeur de H est réalisée deux fois, les deux dissonances sont inégales.
On note que les leptons ont exclusivement des valeurs H _ 0. L'espacement des 5 baryons est particulièrement régulier, occupant jusqu'aux limites des projections, avec H = -4, -2, 2, 4. Cette répartition des baryons possède 3 axes de symétrie : par réflexion par rapport à l'axe vertical 0 h., 6 h.; par réflexion par rapport à l'axe horizontal 9 h., 3 h.; par rotation de 180 º autour d'un axe normal au centre du cadran horaire.
Formulation quantique. Un formalisme quantique en principe complet demanderait qu'on écrive une équation aux valeurs propres contenant l'hamiltonien H, contenant dans le membre de droite l'énergie propre mc2 associée à la fréquence propre ou caractéristique mc2/h. L'hamiltonien devrait s'écrire en y introduisant tous les nombres quantiques y compris K, H et D. On pourrait procéder à une méthode d'approximation linéaire en considérant les effets de H et de D comme des perturbations ajoutant linéairement à l'effet dominant de K et alors on écrirait un développement de termes additifs, et on pourrait espérer séparer les variables K, H et D comme suit.
H
(K, H, D) = H1(K)+H2(H) +H3(D) ... = mc2 (27)C'est là le principe de la relation semi-empirique de Gell Mann et Okubo : elle suppose une logique additive ou en progression arithmétique.[19][20][21][22] Cependant, ce qui précède suggère que cette logique n'est pas la mieux adaptée au problème des masses de la matière électrique et qu'il est préférable d'envisager une logique multiplicative ou en progression géométrique. Une transformation logarithmique permet de séparer K, H et D en des facteurs distincts. En allégeant l'écriture :
LogH = LogH1+LogH2+LogH3 = Log(mc2), (28)
H
(K, H, D) = H1.H2.H3... = mc2. (29)On retombe ainsi sur la formule musicale complète (12).
H
1 = me±c22KH
2 = bHH
3.= bD (30)V. Prédictions
Constante de structure fine a. La constante de structure fine, dont l'inverse vaut 137,04, intervient dans plusieurs formules de la physique atomique et de l'électromagnétisme. Aussi est-il intéressant de voir un nombre très voisin intervenir dans la répartition des fréquences de la matière électrique. La moyenne de x pour les 14 particules plus lourdes que l'électron vaut 137,20. Comme il a été mentionné plus haut, la moyenne des Nos d'octave K pour les mêmes particules est 137,14/12. La moyenne de x est 137,07. Si nous ne savons pas encore pourquoi telle ou telle valeurs de K, de H et de D se réalisent, du moins savons-nous quelque chose sur la moyenne concernant ces valeurs. La Nature a réalisé, dans l'échantillon choisi, une répartition des fréquences qui ont collectivement quelque chose en commun avec le nombre 1/a.
Conjecture d'extrapolation musicale. La distribution de la figure 9 montre un palier suivi d'une ascension. Si l'on envisage le remplissage des octaves, l'abondance des sous-niveaux réalisés augmente graduellement et culmine dans les octaves K = 11 et 12. Du point de vue des régularités musicales, la limite est remarquable puisqu'elle survient à 12 fois la gamme de 12 degrés diatoniques. De plus, le centre de l'accumulation, c'est-à-dire le palier décrit, est sensiblement au centre des octaves bien garnies K = 11 et K = 12, voisin de x =137. L'essence d'un modèle musical étant de reposer sur des nombres et des périodicités, il est naturel de considérer 137 et 144 comme importants pour toute extrapolation et pour toute répétition périodique. Un 2ème palier serait aux environs de x = 274 à 288; les masses prédites ainsi sont aux environs de M = 7,5.106 à 16,8 106 ou de 3,8 Tev à 8,6 Tev.
x = 274 à 288
m = 3,818 Tev à 8,572 Tev (31)
À propos des capacités de prévisions et d'extrapolations du présent modèle musical, voici un exemple basé sur l'histoire. Reportons-nous en 1958, alors qu'on ne connaissait que 8 particules de notre échantillon, les plus légères jusqu'au X-.[18] La distribution arrêtée à cette limite donne moins que 137 comme moyenne et elle ne touche pas tout à fait x = 137, mais elle suggère un palier à 137 et elle suggère la conjecture qu'il y ait une suite symétrique avec la branche ascendante que nous connaissons. Depuis 1958, les accélérateurs puissants ont permis de compléter la liste de notre échantillon en ajoutant certaines particules plus lourdes que le X-, mais aucune plus légères que X-. Cette observation conforte notre principe de clôture ci-haut. En revanche, il faudra reformuler notre principe de clôture, si effectivement les particules prédites aux masses extrêmes existent.
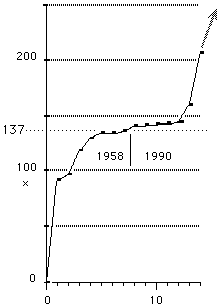
Fig. 9. Distribution par valeurs croissantes des masses. Il y a un plateau et un point d'inflexion au voisinage de x = 137; le plateau suivant serait aux environs de x = 274.
VI. Matière électrique et musicalité
Les régularités remarquables de notre échantillon paraissent lui appartenir en exclusivité, si nous le comparons aux autres catégories de particules que nous avons pu définir.
Baryons charmés. Nous avons choisi d'exclure de notre échantillon, figuré à nouveau à la figure 10, 4 baryons chargés charmés S. Nous expliquons cette nécessité. Comme le montre la figure 11, ils respectent les limites horaires du nonet, car ils tombent entre H = 1 et 3, mais ils présentent des hauteurs h en discordance marquée avec les Nos de gamme. L'analyse des distances mutuelles à la figure 8 confirme objectivement cette discordance. Admettant qu'il existe un principe de saturation pour les baryons à mesure que se produit le remplissage décrit ci-dessus, nous pouvons expliquer qu'il n'y ait plus de places exactes pour ces baryons charmés quand arrive leur tour puisqu'ils sont les plus lourds de la liste des baryons S. D'après les principes d'exclusion ci-haut, ils sont repoussés par le pion qui doit être seul à H = 1 et par le boson de jauge qui doit être seul à H = 3; de plus, ils subissent la concurrence des baryons S + et ·S - déjà logés au voisinage de H = 2. Le fait que ces baryons, auxquels la CDQ (chromodynamique quantique) assigne un quark charmé c, réclament collectivement un traitement distinct, dans notre modèle musical, peut être considéré comme une confirmation mutuelle de la CDQ et de notre modèle.
Autres particules. Il reste 3 catégories de particules à examiner dans notre modèle musical : chargées non S, neutres S et neutres non S. Nous avons cherché si elles suivent la règle de gamme, ce qui requiert une connaissance suffisamment précise de la masse. Une erreur de 0,2 % sur la masse cause une incertitude de 0,033 sur H. Ce critère exclut la plupart des particules non S énumérées dans les tables. Les résultats apparaissent aux figures 12, 13 et 14, qui sont loin de manifester des régularités évidentes.
Élémentarité. La comparaison des figures 10 à 14 montre que notre échantillon de particules chargées obéit d'une façon privilégiée à notre modèle musical, manifestant des symétries suggestives d'un contenu physique important. Il est naturel de considérer ces particules comme particulièrement fondamentales et représentatives de ce qu'est l'électricité : elles sont la matière électrique par excellence. Les fréquences de de Broglie que cette matière peut adopter établissent entre elles des rapports musicaux particulièrement harmonieux.
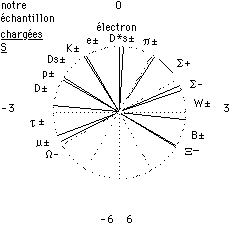
Fig. 10. Reprise de la figure 7, pour 15 particules chargées S de notre échantillon. Pour comparer avec les figures suivantes.
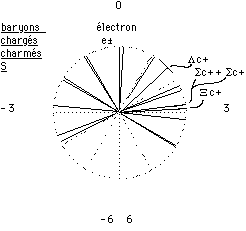
Fig. 11. Comme la figure 10, en ajoutant les 4 baryons charmés.

Fig. 12. Comme la figure 10, pour 10 particules chargées non S. Cette figure et les deux suivantes sont loin de montrer un aspect de régularité comme la figure 10. L'électron apparaît comme référence.
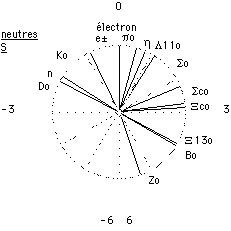
Fig. 13. Comme la figure 12, pour 12 particules neutres S.
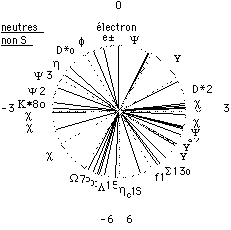
Fig. 14. Comme la figure 12, pour 33 particules neutres non S.
Disons que la matière électrique fondamentale possède une musicalité supérieure. Prenant la musicalité comme critère d'élémentarité, nous proposons l'hypothèse que la matière électrique fondamentale soit constituante élémentaire de toute autre matière, chargée ou neutre : elle serait la matière élémentaire elle-même. En d'autres termes, l'électricité serait l'élément ultime dont les combinaisons formeraient toute matière.
Cette vue s'accorde avec certains aspects du modèle standard. Dans ce modèle, si l'on excepte le boson de jauge neutre Zo, toutes les particules désignées comme élémentaires et ayant une masse notable au repos sont chargées. Les voici : e±, µ±,
t±, W±; les quarks u etSignalons certaines publications traitant de la nature de l'électricité. Schrödinger
[23] et Wilson rapporté par Bachelard [26][27] ont affirmé que l'électricité est matière, que l'électricité n'est pas un caractère s'ajoutant à de la matière. Langevin [28] a mis en évidence qu'il ne peut pas exister de quantité d'électricité sans masse associée et il a envisagé une synthèse réunissant Électricité, Optique et Mécanique. Weyl a envisagé l'hypothèse que la matière soit un fait de nature purement électrique.[29]Ainsi l'électricité serait à la fois matière et vibration. Cela est assez éloigné de la conception poétique qu'illustra le peintre Raoul Dufy en 1937, lorsqu'il créa une murale intitulée par lui "La Fée Électricité".[30] Dans un langage plus scientifique, la conception d'un philosophe à ce propos est tout autre.
"L'électricité n'est ni une fée, ni un Dieu, ni une entité métaphysique... On pourrait même se disputer pour savoir ce qu'elle peut être en soi, comment elle peut contribuer à l'harmonie du monde... que peut-être cette matière électrique qui échappe aux sens, c'est-à-dire aux détecteurs obligatoires de la réalité?... Jamais nous ne saurons, à son propos, plus que ce que nous n'en comprenons par les fonctions mathématiques". Bénézé [31]
Poursuivant l'idée de Bénézé, disons que cette matière électrique fait plus que contribuer à l'harmonie du monde : elle est harmonie elle-même.
Couleurs perceptuelles. Le modèle musical est basé sur un rapprochement avec la perception visuelle, lorsqu'on examine le cercle énergétique des couleurs. L'aspect du cercle horaire de la figure 7 rappelle celui d'un cercle énergétique des couleurs, dans lequel les pourpres, couleurs inexistantes dans le spectre, occuperaient le secteur vide entre 4 h. et 8 h. du cadran horaire.[24][25] Les pourpres sont des couleurs faisant le lien perceptuel entre le rouge extrême et le violet extrême. Dans l'ordre des énergies croissantes, le rouge est à gauche et le bleu est à droite. Le jaune-vert se placerait à l'opposé des pourpres et entourerait l'électron; le proton serait dans le jaune-orangé. (Fig. 15)

Figure. 15. Cercle énergétique des couleurs. Les couleurs perceptuelles forment une suite fermée sur elle-même, qu'on peut ordonner selon un cercle. Les photons d'énergie unique du spectre déterminent, entre les bornes approximatives de 8000 ![]() et de 4000
et de 4000 ![]() , environ les deux-tiers de ce cercle. L'autre tiers est déterminé par les pourpres, couleurs inexistantes comme telles dans le spectre.
, environ les deux-tiers de ce cercle. L'autre tiers est déterminé par les pourpres, couleurs inexistantes comme telles dans le spectre.
VII. Les forces fondamentales
Forces gravitationnelles. Reprenons les raisonnements qui nous ont conduits à postuler un modèle musical. Il faut d'abord écarter tout espoir de déceler ces vibrations et les fréquences de de Broglie directement. Assurément, les règles énergétiques nous permettent d'imaginer un processus d'annihilation totale de la masse m en un seul photon, porteur de la fréquence cherchée. Nous pourrions alors mesurer cette fréquence sinon l'observer directement. Ainsi, l'annihilation mutuelle d'un électron positif et d'un électron négatif au repos donne deux photons ayant l'un et l'autre une fréquence, mesurable, égale à la fréquence de de Broglie assignée à chacun des électrons. Mais la vibration manifestant cette fréquence est celle d'un photon, non pas celle de particule. L'annihilation demanderait l'action de l'une de trois forces fondamentales reconnues en physique des particules : forte, faible ou électromagnétique, lesquelles ont conduit au modèle standard.
Cependant, il existe des processus moins destructeurs mais indirects pour atteindre ces fréquences. Admettant l'existence de ces fréquences, la méthode de la balance, c'est-à-dire, en principe, de la gravitation, est à notre service. C'est l'intervention de la force gravitationnelle qui permet de constituer la collection de fréquences que nous avons considérées.
Le modèle standard, malgré ses règles de quantification bien vérifiées, s'est montré jusqu'ici incapable de résoudre le problème des masses.[32][33] La nécessité d'invoquer la force gravitationnelle, 4ème force fondamentale, pour manifester les rapports des masses et des fréquences suggère que cette manifestation serait liée à la 4ème force et pourrait justifier des règles de quantification nouvelles, telles que celles suggérées ci-dessus.
Une synthèse. Les régularités mises ici en évidence réunissent des leptons, des bosons de jauge et des hadrons chargés, sans qu'on puisse reconnaître de différences systématiques entre ces catégories. Le modèle musical réalise donc une sorte de synthèse des 3 forces fondamentales, électromagnétique, faible et forte, synthèse qui est en principe l'objet du modèle standard. Puisque ce sont les particules chargées qui répondent le mieux à la manière du modèle musical d'analyser les masses, et puisque les harmonies constatées proviennent des mesures gravifiques, on aperçoit un espoir que ce modèle puisse aussi inclure la 4e force, la force gravitationnelle, dans sa synthèse, conformément à la vision de Langevin d'unifier Électricité et Mécanique.
Nous suggérons que, musicalité et élémentarité se trouvant associées spécialement à la force électromagnétique et à la force gravitationnelle, ces deux forces seraient plus fondamentales que les deux autres et les expliqueraient. Il faudra poursuivre les études dans ce sens, continuant les travaux de Sternheimer et de Koschmieder en plus des nôtres.[34][35]
VIII. Conclusion
Nous voyons que le modèle musical confirme à sa manière la réalité du caractère vibratoire des particules, selon l'équation de de Broglie. Leurs fréquences ne sont pas perceptibles individuellement, mais, si elles n'avaient aucune réalité physique, on imagine mal comment le modèle musical pourrait s'appliquer aux rapports de masses qui leur correspondent.
IX. Remerciements
Je remercie plusieurs collègues pour des discussions profitables et pour leur encouragement : Pierre Auger, Yves Gingras, Jean-Paul Longavesne, Paul Lorrain, Dudka Smoje, Joël Sternheimer. Pierre Auger m'a aidé à faire les calculs probabilistes.
X. Références
[1] H. Rauch 1991, Interaction d'ondes matérielles à l'aide de neutrons, Ann. fond. L. de. B.,15, 4, 373-401
[2] Barbara Goss Levi 1991, (Des atomes comme ondes nouvelles dans les interféromètres), Physics Today 44, 7, 17-20
[3] Louis de Broglie 1923, Ondes et quanta, C. r. 177, 507
[4] Jozef Hurwic 1988, in Présence de Gaston Bachelard, réd. C. Atias et J. Le Moigne, Univ. Aix-Marseille III, 51-2. (Dans les références [
4] à [8], les soulignés sont de nous).... le concept de Louis de Broglie attribuant le caractère ondulatoire aux corpuscules matériels était à l'origine de la création par Erwin Schrödinger de la mécanique ondulatoire. Mais la théorie de Schrödinger est basée surtout sur les travaux du mathématicien irlandais William Rowan Hamilton... La fonction
[5] C. Daviau 1990, Électromagnétisme, monopôles magnétiques et ondes de matière dans l'algèbre d'espace-temps, Ann. fond. L. de B. 15, 373-390
Lorsque Louis de Broglie a associé une onde au mouvement de toute particule, il était clair, dans son esprit, que cela généralisait la situation du photon dans l'onde électromagnétique de la lumière. L'onde associée à l'électron devait avoir un lien étroit avec l'électromagnétisme. Par la suite, une autre interprétation a prévalu, où le carré du module de l'onde donne la probabilité de présence de la particule. C'est un point de vue que De Broglie a accepté à contre-coeur, puis contre lequel il a osé s'élever à partir des années 50.
[6] Albert Messiah 1959, Mécanique quantique, Tome II, Dunod, 42
.. nous associons à chaque particule matérielle une onde dont la fréquence circulaire
[7] Banesh Hoffmann et Michel Paty 1981, L´étrange histoire des quanta, 80-81, Seuil
... nous arrivons à la conclusion que les particules sont animées de vibrations. ..Oublions pour un instant les ondes et concentrons-nous sur les vibrations. Nous pouvons, chose remarquable, déterminer leur cadence exacte de vibration... nous en avons tiré un modèle de particule doué d'une cadence de vibration donnée... Concentrons-nous maintenant sur la vibration pure...
[8] Fritjof Capra 1979, Le Tao de la Physique, Tchou
"Toutes choses sont des agrégats d'atomes qui dansent et qui par leurs mouvements émettent des sons. Lorsque le rythme de la danse varie, le son produit change également. Chaque atome chante perpétuellement sa chanson, et le son, à chaque instant, crée des formes lourdes ou subtiles". [Un lama thibétain]...La similitude de cette vision et de celle de la physique moderne devient particulièrement remarquable lorsque nous nous rappelons que le son est une onde possédant une certaine fréquence qui change lorsque le son varie, et que les particules sont aussi des ondes aux fréquences proportionnelles à leurs énergies.
[9] Erwin Schrödinger 1952 (1984), L'image actuelle de la matière, 4 septembre, Gesammelte Abhand., Vieweg, 4, 503-526
[10] PDG 1988, Phys. Letters B, 204, avril
[11] PDG 1990, Phys. Letters B, 239, avril
[12] Joël Sternheimer 1983, Musique des particules élémentaires, C. r., 297, II, 829-834
[13] Joël Sternheimer 1986, Musique des particules élémentaires, Rev. Biomath., Nº 94 (88), 1-47
[14] Pierre Demers 1983, Modèle biomathématique unitaire descriptif de toutes les perceptions humaines, Rev. biomath., Nº 81 : 13-58
[15] C. Rubbia 1990, Introduction par le Directeur général, CERN 1990 Rapport annuel I, 5-6
[16] A. Laforgue 1990, Les propriétés chirales de la matière vivante et la physique quantique, Ann. fond. L. de B. 14, 391-425
[17] Helmut Reis 1985, (Les 100 ans de la formule de Balmer. Histoire de sa géométrie), Verlag für systematische Musikwissenschaft Gmbh, Bonn
[18] Pierre Demers 1958, Ionographie, PUM
[19] Luc Valentin 1989, Noyaux et particules, Hermann
[20] T. Takabayasi 1964, (Modèle d'oscillateur pour les particules fondamentales de la symétrie unitaire), N. Cim. 33, 668-672
[21] Moshé Flato et Joël Sternheimer 1964, Sur les formules de masses fortes et électromagnétiques des particules élémentaires, C. r., 259, 3455-8
[22] D. Bohm, Moshé Flato, F. Halbwachs, P. Hillion et Jean-Pierre Vigier 1965, (Sur le caractère "espace-temps" des symétries internes des particules élémentaires), N. Cim., 36, 672-5
[23] Erwin Schrödinger ca 1930 (1984), (Quelle est la nature de l'électricité)? (Koralle, 110-2), Gesammelte Abhand., Vieweg, 4, 321-3
[24] Jean-Paul Longavesne et Pierre Demers 1986, texte, soumis à Interface de l'ACFAS
[25] Jean-Paul Longavesne et Pierre Demers 1987, Ann. ACFAS, 55, 272
[26] H. A. Wilson 1934, (Les mystères de l'atome), 28
[27] Gaston Bachelard 1951, L'activité rationaliste de la physique contemporaine, PUF, 107-8
[28] Paul Langevin 1947, L'évolution expérimentale de la science électrique, Atomes, Nº 11, 56-60
[29] Hermann Weyl 1921, Temps, espace, matière, trad. G. Gillet et R. Leroy, Blanchard, 178- 179
[30] Raoul Dufy 1937, La Fée Électricité, murale, École Polytechnique de Montréal
[31] Georges Bénézé 1961, Le nombre dans les sciences expérimentales, 62, 65 PUF
[32] P. Hasenfratz et I. Montvay 1983, Phys. Rev. Letters 50, 309
[33] Maurice Jacob 1988, in CERN 1988, Rapport des activités dans les divisions, Division physique théorique, 7-10
[34] E. L. Koschmieder 1988, N. Cim. A99, 555
[35] Pierre Demers 1991, communication soumise au 59ème Congrès ACFAS
_________________________________________________________________
Caractères spéciaux
a c h p Y µ t S X L D ∂ ¶ x x X X h h # s A B C D E F e S M n_____________________________________________________________