Précédent : EquipartitionSphere http://www.lisulf.quebec/EquiSphere.html Atomesentetrades http://www.lisulf.quebec/Atomesentetrades.html PrecessionSpin http://www.lisulf.quebec/PrecessionSpin.html Quebecium http://www.lisulf.quebec/quebecium.qc.ca

Traduction interdite Tous droits de traduction réservés

L'examen des dimensions angulaires des cônes de la précession du spin de l'électron montre que quatre de ces cônes s'ajustent ensemble pour donner une figure qui s'inscrit dans un tétraèdre régul;ier. Suivant la théorie quantique, l'ouverture des cônes est 109,471o. Pour la commodité de la démonstration, attribuons aux cônes des dimensions finies avec une génératrice de 5 cm; la base circulaire de chacun a alors un diamètre de 8,165 cm. Assemblés ensemble ayant leurs sommets communs, un cône touche chacun des 3 autres selon une génératrice.

La proposition s'étend à toutes les particules de spin 0,5 donc au proton et au neutron et aux fermions en général.

Ce résultat peut s'énoncer autrement.

À cause de la théorie quantique de sa précession, le cône de précession du spin d'une particule de spin 0,5 est associé au tétraèdre régulier.

Une particule de spin 0,5 génère un tétraèdre régulier ou contient un tétraèdre régulier virtuel, de la manière décrite. C'est ce que nous appellerons une association directe entre le spin 0,5 et le tétraèdre régulier.

On peut songer à étendre ce résultat aux autres valeurs du spin et aux autres solides réguliers convexes. Nous allons voir qu'en effet on peut reconnaître une association de certaines valeurs du spin avec ces 5 solides : tétraèdre, cube, octaèdre, dodécaèdre et icosaèdre. L'association avec le dodécaèdre et l'icosaèdre est indirecte.

Voici des figures concernant le spin 0,5 et expliquant ce que nous entendons par association directe.

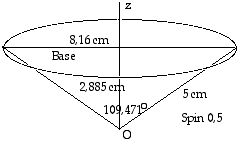
Fig. 1. Un cône d'ouverture 2thêta =109,471o, de génératrice 5 cm. C'est le cas du cône de précession du spin 0,5.

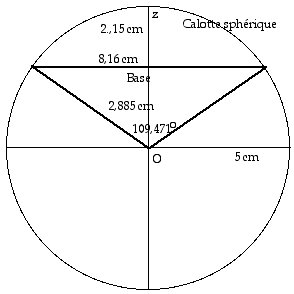
Fig. 2. Un cône d'ouverture 2thêta = 109,471o peut être inscrit et centré dans une sphère de rayon 5 cm. La génératrice mesure 5 cm. Vue en coupe.

Fig. 3. Deux cônes d'ouverture 2thêta = 109,471o ayant un sommet commun et une génératrice en commun, vue dans le plan comprenant la génératrice et les axes des 2 cônes. 70,529o = 180o - 109,471o est l'angle dièdre entre les plans des 2 bases circulaires. C'est aussi l'angle dièdre du tétraèdre.

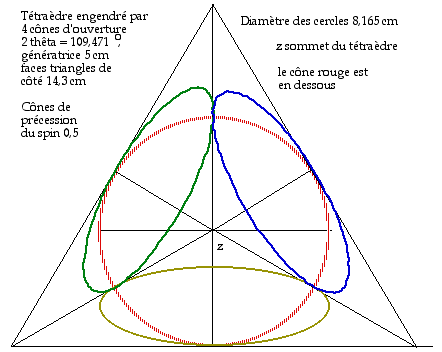
Fig. 4. Tétraèdre engendré par 4 cônes de précession du spin 0,5.

Des cônes égaux, de précession ou autres, peuvent engendrer un solide régulier, de la manière exposée graphiquement ci-dessus pour le cas de 2thêta = 109,471o et le tétraèdre. Il faut et il suffit que leur ouverture 2thêta, double de leur angle thêta, soit égale au supplément de l'angle dièdre de ce solide. Le sommet des cônes est placé au centre du solide. L'angle dièdre du solide doit être le supplément de l'ouverture des cônes. S'il s'agit de cônes de précession d'un spin déterminé, nous dirons alors qu'il y a une association directe entre ce spin et ce solide régulier, que le spin des particules en question génère ce solide.

Dans notre présente enquête, il faut donc comparer deux tableaux : celui des angles 2thêta d'ouverture des cônes de précession du spin aux diverses valeurs du spin, d'une part et celui des suppléments de l'angle dièdre des divers solides de Platon.

thêta = arccos (Iprojection/Ã(I(I+1)))

Iprojection peut prendre au moins les 2 valeurs ±I. Les autres valeurs, s'il en est, sont espacées de l'unité sur une échelle allant de -I à I .

-I, -I+1, -I+2, ... I-2, I-1, I

En confondant les signes ±, le spin 0,5 a une projection 0,5, le spin 1 a une projection non nulle égale à 1 et la projection zéro, etc. Angles en degrés.

On a repéré cinq valeurs du spin manifestant une association directe avec l'un de 3 solides de Platon : le tétraèdre, le cube et l'octaèdre. On a repéré une valeur du spin manifestant une association indirecte avec l'un et l'autre de 2 solides de Platon : le dodécaèdre et l'icosaèdre.

Ces tableaux nous apprennent ce qui suit.

Il y a association directe d'un spin avec un solide quand l'ouverture du cône de précession est égale au supplément de l'angle dièdre de l'un des solides.

Tétraèdre. Le spin 0,5 projection 0,5, ce que nous notons 0,5/0,5 et le spin 3/2 avec le tétraèdre. Quatre cônes de précession génèrent un tétraèdre.

Cube. Les spins 1/1 et 8/6 avec le cube. Six cônes de précession génèrent un cube.

Octaèdre. Le spin 2/2 avec l'octaèdre. Huit cônes de précession génèrent un octaèdre.

Dodécaèdre. On observe une affinité évidente du spin 4/2 avec le dodécaèdre, le cône de précession ayant un angle 126,870o, double de l'angle 63,435o, appartenant au dodécaèdre. Cela suggère ce qui ressemble à une association directe. Il faudrait découvrir une raison d'introduire un facteur 2 dans la comparaison. Ce n'est pas la 1re fois que se présente la nécessité d'un facteur correctif non prévu par la théorie, dans la comparaison entre valeurs théoriques et expérimentales. Un cas bien connu, celui de la déviation gravitationnelle de la lumière, impliquait une théorie d'Einstein. Le cas du facteur de Landé touche notre présent domaine, celui du spin. Le facteur de Landé est 2 augmenté de 0,003; ici le facteur est exactement 2. Rappelons encore l'existence d'un facteur valant exactement 2 quand on compare le moment cinétique propre s et le moment orbital l le plus petit : s vaut 0,5 et l vaut 1.

Hypothèse. Cône virtuel,. En établissant ci-dessus la condition d'une association directe, on a admis intuitivement l'hypothèse que les cônes sont impénétrables l'un par l'autre. Mais réduisons arbitrairement cette exigence : nous allons admettre que le cône de précession du spin 4/2 a une ouverture angulaire efficace moitié de l'ouverture prévue, avec une zone d'inefficacité correspondante. Il serait parfaitement pénétrable dans une zone extérieure de son angle solide, au point de se conduire comme un cône d'ouverture 63,435o, et non 126,870o. Le spin 4/2 aurait un cône de précession virtuel d'ouverture 63,435o.

Voilà certes une hypothèse ad hoc, mais mieux vaut une hypothèse ad hoc que pas du tout. Référence la théorie du calorique qui a fait la fortune, un temps, de Lavoisier.

Pour ces raisons, nous dirons qu'il existe une sorte d'association que nous appellerons indirecte du spin 4/2 avec le dodécaèdre.

Douze cônes virtuels de précession génèrent un dodécaèdre.

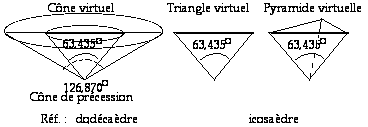
Fig. 5. Cône virtuel, triangle virtuel, pyramide virtuelle

Icosaèdre. L'angle 63,435o, se rencontre encore dans l'icosaèdre : il sous-tend une arête vue du centre de figure. Reprenons notre cône virtuel qui vient de nous servir pour le dodécaèdre. Il constitue une réduction du cône de précession ayant une ouverture double, soit 126,870o. Eh bien, nous allons le réduire encore, cette fois en ne conservant de sa base circulaire qu'un diamètre. Ainsi réduit, il devient un triangle isocèle d'ouverture 63,435o.ayant le même sommet que le cône de précession. Notre cône virtuel est devenu un triangle virtuel, la génératrice du cône virtuel servant aux 2 côtés égaux du triangle isocèle. Notre triangle virtuel n'est pas équilatère, il est isocèle, les 2 côtés ègaux étant un peu plus courts que l'autre.

Trois de ces triangles réunis composent une pyramide de base triangulaire, 3 diamètres formant un triangle équilatéral soit une face d'un icosaèdre. Vingt de ces pyramides soit 60 segments de droite génèrent un icosaèdre en occupant tout l'angle solide. Étant donné les répétitions, il suffit de 30 segments de droite. Nos pyramides sont des tétraèdres non réguliers, un peu écrasés comparés au tétraèdre régulier. Nous les appellerons des pyramides virtuelles de précession

Vingt pyramides virtuelles de précession génèrent un icosaèdre.

On peut difficilement comprendre la géométrie 3D, sans se fabriquer des figures 3D en papier. Ici, il faut des cônes et des pyramides en plus des formes de Platon. Nous donnons des patrons pour les fabriquer.

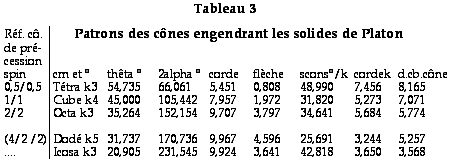
Cônes. Un cône se fabrique à partir d'un cercle plan en raccourcissant son pourtour et en conservant un secteur dont on réunit les extrémités. Le centre du cercle devient le sommet du cône, son rayon, la génératrice du cône. L'angle du secteur conservé est 360o - 2alpha, l'échancrure est 2alpha, d'autant plus petite que l'ouverture 2thêta du cône est plus grande. Voici la relation.

2alpha = 360 o(1-sinthêta)

Diamètre du cercle base du cône obtenu = 10(360o -2alpha)

Dans le tracé nécessaire, 3 données sont utiles. Avec un rayon de 5 cm.

Corde du secteur échancré = 10sinalpha

Flèche de cette corde = 5 - 5cosalpha

Pour repérer k génératrices équidistantes sur le cône, cordes(k) divisant le secteur conservé en k arcs égaux, chacun = s. cons./k.

corde(k) = 10(sin(360o - 2alpha)/k)

Ces génératrices tracées sur les cônes facilitent leur assemblage.

Pyramides. Dans le cas de l'icosaèdre, on peut naturellement fabriquer des cônes d'ouverture 41,810´, mais il est démonstratif de fabriquer des pyramides virtuelles dont les côtés égaux ont l'ouverture 63,435´ et d'en agencer 20 côte à côte autour d'un centre commun. On trace le patron à l'intérieur d'un cercle de rayon 5 cm. Les dimensions sont comme suit.

Ouverture du triangle 63,435´, cordes 5,357 cm, angle entre les cordes 63,435´.

Suite..GQ2/2

GQ2sur2 GQ1sur2 Suivant :GQ2sur2 http://www.lisulf.quebec/GQ2sur2.html