
GQ2sur2 GQ1sur2 http://www.lisulf.quebec/GQ1sur2
EquipartitionSphere http://www.lisulf.quebec/EquiSpherehtml Atomesentetrades http://www.lisulf.quebec/Atomesentetradeshtml PrecessionSpin http://www.lisulf.quebec/PrecessionSpinhtml Quebecium http://www.lisulf.quebec/quebecium.qc.ca
Traduction interdite Tous droits de traduction réservés
Système du Québécium
Géométrie quantique
**/**
Pierre Demers
Catégories duales des solides de Platon
La géométrie des solides de Platon est le domaine par excellence des angles et des nombres entiers, sources de symétries, et du discontinu dans ces domaines. Les relations de dualité entre solides de Platon conduisent à les diviser en 3 catégories. Nommées d'après le solide de moindre nombre de faces qu'elles contiennent, les voici.
Catégories duales des solides de Platon
1. Du tétraèdre. Le tétraèdre étant dual de lui-même, cette catégorie ne contient qu'un seul membre, le tétraèdre.
2. Du cube. Cube et octaèdre.
3. Du dodécaèdre. Dodécaèdre et isosaèdre.

Fig. 6. Catégories des solides de Platon.
Catégories angulaires des solides de Platon
Ces catégories se ramènent à 2 si on considère l'expression des dimensions angulaires et autres apparaissant au Tableaux 4 à 7. Les dimensions autres sont équivalentes à des dimensions angulaires.
En effet, on remarque l'intervention, dans ces tableaux, outre l'unité, des 5 premiers nombres premiers 2, 3, 5, 7 et 11, soit tels quels, soit dans des fonctions puissances ou trigonométriques que nous appellerons globalement angulaires.
Or le nombre 5 n'apparaît que dans la 3e catégorie duale ci-dessus du dodécaèdre et cette catégorie renferme en outre les nombres premiers 7 et 11.
Cela suggère de distinguer 2 catégories angulaires seulement, en groupant en une seule les catégories duales 1 et 2.
Catégories angulaires des solides de Platon
1. Les nombres premiers qui apparaissent sont 1, 2 et 3. Ils apparaissent dans chaque solide. Renferme le tétraèdre, le cube et l'octaèdre.
2. Les nombres premiers qui apparaissent sont en outre 5, 7 et 11. Renferme le dodécaèdre et l'icosaèdre.
On rencontre dans chacun de ces 2 solides arccos(1/├5) = 63,435o ou son supplément = arccos(-1/├5) = 115,565o, (soit(arccos(▒1/├5)). L'impair 11 est prÄsent dans le dodécaèdre
Les nombres 3 et 5 jouent des rôles complémentaires quand on passe de l'une catégorie à l'autre. En tout et partout, les premiers apparaissant sont (1), 2, 3, 5, 7 et 11.
On voit aux Tableaux 1 et 2 que la catégorie 1 s'accorde avec l'association directe et la catégorie 2, avec l'association indirecte. L'explication suit.
Catégories angulaires des spins
Les angles d'ouverture 2thêta des cônes de précession dépendent du quotient I/├(I(I+1)), où nous apercevons 2 nombres : I et I+1. S'ils sont semi-entiers, nous les supposons écrits sous la forme d'une fraction avec dénominateur 2. Dans les 5 cas où nous avons trouvé génération de solides de Platon par un spin par association directe, cette formule contient constamment les nombres premiers 2 et 3, en plus de l'unité. Dans le seul cas où nous avons trouvé une association indirecte, cette formule contient le nombre 5.
Catégories angulaires des spins
1. Le nombre 5 n'apparaît pas. Le nombre 3 apparaît. Génèrent le tétraèdre, le cube et l'octaèdre.
2. Le nombre 5 apparaît. Génèrent le dodécaèdre et l'icosaèdre.
Il y a accord avec les catégories angulaires des solides de Platon.
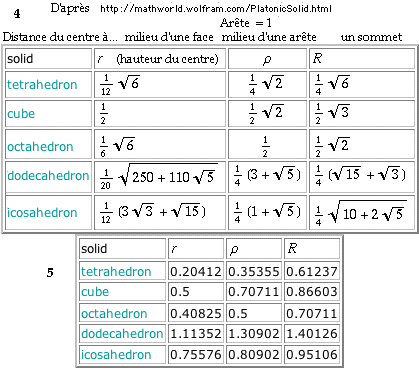
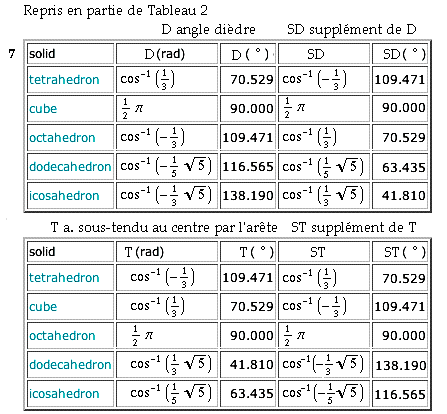
Tableaux 4 à 7
Dimensions angulaires et autres des polyèdres de Platon
http://mathworld.wolfram.com/PlatonicSolid.html

Le spin des photons de la lumière
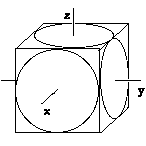
Fig. 7. Création d'un système trirectangle xyz par 6 bosons de spin 1/1.
Les photons sont des bosons ayant le spin égal à 0, 1 ou un autre entier. Ils ont une tendance à coexister tous dans le même état. Bornons-nous aux photons de spin 1. Ils pourraient générer des cubes, correspondant au spin 1/1 et rassemblant 6 photons. L'évocation ou la génération d'un système de coordonnées cartésiennes apparaît bien appropriée concernant des particules qui occupent avec facilité tout l'espace 3D. De façon figurée ou non, nous dirons que les photons transportent avec eux la définition de l'espace.
Le cube, seul parmi les solides de Platon, a la faculté de dallage indéfini de l'espace 3D. Les cristaux dallent l'espace 3D mais parmi eux, seuls ceux qui ont la forme cubique sont des solides de Platon.
Cônes et polyèdres, une vue rassembleuse
Dans ce qui précède, nous n'avons envisagé que des cônes de bases circulaires ayant des ouvertures choisies. Mais assurément, nous pouvons envisager des cônes ayant toutes les ouvertures angulaires entre 0 et 180 degrés et une génératrice constante. Nous tenons là une occasion de rassembler les 5 solides de Platon dans un diagramme unique de distribution angulaire. Des angles privilégiés apparaissent.

Fig. 8. Distribution angulaire des cônes générateurs des solides de Platon. L'ouverture du cône est l'angle SD des Tableaux 2 et 7. L'extrapolation suggère 2 cas limites imaginaires. L'angle 0o donnerait un nombre infini de faces soit une sphĆre. L'angle 180o donnerait un solide de 2 faces sans épaisseur.
On peut imaginer les cônes remplacés par des boules uniformes prêtes à se disposer régulièrement et concentriquement à la distance voulue pour que, vues d'un point central, elles sous-tendent un angle voulu. Par exemple, elles flotteraient dans un liquide de densité ajustée. Elles auraient une tendance à former des amas organisés en sphères de 20, 12, 8, 6 ou 4 boules dessinant des triangles, des cubes et des pentagones. Intuitivement : les amas de 4 seraient favorisés parce qu'ils sont compacts et résistent aux déformations. Les autres amas auraient des vides et seraient déformables. Dans le cas de l'icosaèdre, les boules devraient se compénétrer.
Conclusion
Aspect proprement mathématique, la théorie quantique du spin conduit à générer les solides de Platon. La relation semble bien établie et va dans le sens spin vers solides. Ce qui unit les 2 domaines est leur caractère commun de discontinuité et de quantification au sens du terme en théorie des symétries.
On pourrait chercher à étendre les résultats à des solides autres que platoniques, en 1er lieu, aux 4 solides réguliers concaves dw Képler-Poinsot.
Ces résultats sont à sens unique; le sens opposé, solides vers spin, soit une théorie géométrique des solides conduisant à la théorie quantique du spin paraît en effet difficile à atteindre à cause d'un principe général d'information : l'information contenue dans les 5 formes de Platon ne peut être équivalente à celle contenue dans la totalité des cônes de précession des spins possibles, totalité à priori indéfinie.
Reprenons les 3 catégories duales de solides platoniques.
La 1re est liée principalement au spin 0,5 du fermion qu'est l'électron. Réciproquement, le fermion ne peut être associé qu'à la 1re, soit au tétraèdre. La 2e paraît liée principalement au spin 1 du boson qu'est le photon. La 3e catégorie pose problème elle paraît liée aux bosons mais la nécessité d'un facteur 2 n'est pas expliquée. Des particules de spin 4/2 existent-elles, ou seraient-elles imaginaires et une vue de l'esprit?
Nous avons eu l'occasion de reconnaître l'importance, rarement signalée, des nombres premiers dans la définition des solides de Platon, et dans leur association aux propriétés quantiques des atomes.
Aspect philosophique, il y a de quoi réfléchir sur l'existence et la nature de l'espace où nous évoluons d'une part et sur la justification de la théorie des quanta d'autre part. Nous devons admettre que la quantification n'est pas confinée à l'atome microscopique.
Il est réconfortant de savoir maintenant que l'existence des figures géométriques bien connues est là pour concrétiser en quelque sorte l'intervention de nombres, entiers et premiers, dans le fonctionnement des atomes autour de nous.
La revanche des Anciens?
La doctrine de Platon avec ses idées sur les 4 ou les 5 éléments géométriques constituants ultimes de l'univers aurait-elle en définitive quelque justification et devrait-elle revenir à la mode?
La doctrine des balles lumineuses de Newton, honnie au 19e siècle, passe de nos jours pour une anticipation intéressante de la dualité d'aspect de la matière, onde et corpuscule.
On peut accorder aux Anciens cherchant à expliquer la matière, la priorité d'une anticipation au sujet de l'importance de formes exigeant des nombres entiers et premiers.
Le présent travail suggère que Platon et ses contemporains n'avaient pas complètement tort : le tétraèdre n'est pas la substance du feu, mais il est dans une correspondance indéniable, jusqu'aux confins de l'univers, avec tous les électrons, qui nous envoient des messages par les ondes électromagnétiques, dont certains sont des souvenirs d'un monde très ancien.
Annexe. Patrons
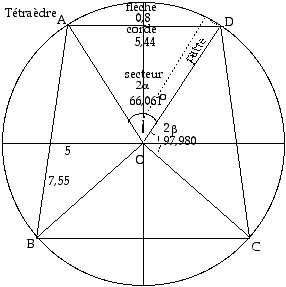
Fig. 9. Tétraèdre régulier associé aux spins 0,5/0,5 et 3/2 Patron sur une feuille plane servant à obtenir un cône d'ouverture 109,471o du spin 0,5. Rayon 5 cm. La patte sert à raccorder par collage les lignes OA et OD. Quatre de ces cônes génèrent un tétraèdre régulier
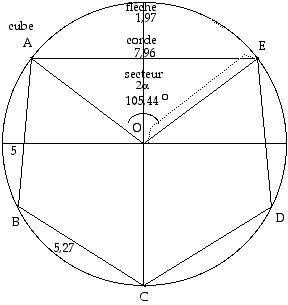
Fig. 10. Cube associé au spin 1/1. Patron donnant un cône d'ouverture 90o. Six de ces cônes génèrent un cube.
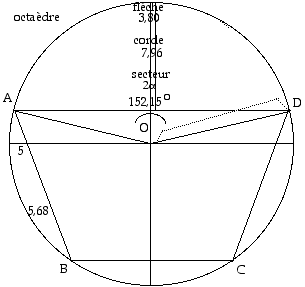
Fig. 11 Octaèdre associé au spin 2/2. Patron donnant un cône d'ouverture 70,529o. Huit de ces cônes génèrent un octaèdre.
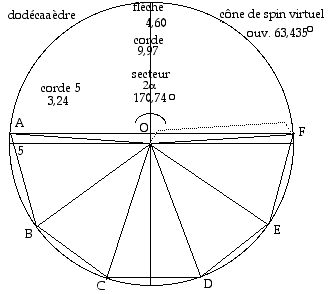
Fig. 12. Dodécaèdre associé au spin 4/2. Patron donnant un cône d'ouverture d'ouverture 63,435o, ce qui est l'ouverture du cône virtuel de précession du spin 4/2. Douze de ces ces cônes génèrent un dodécaèdre.
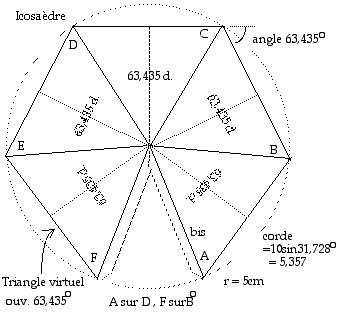
Fig. 13. Icosaèdre régulier associé au spin 4/2. Patron donnant 2 pyramides à base triangulaire, le côté de la base triangulaire mesure 63,435 degrés. On plie selon les lignes radiales pleines, puis on exécute deux raccordements. Vingt de ces pyramides génèrent un icosaèdre inscrit dans une sphère de rayon 5 cm.
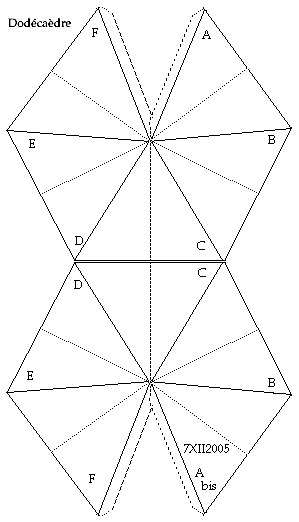
Fig. 14. Ce patron, doublé du précédent avec jonction, permet de fabriquer 4 pyramides d'un tenant

Fig. 15. Tout en papier. Le tétraèdre en 4 cônes, le cube en 6 cônes et l'octaèdre en 8 cônes. Le tétraèdre, le cube et l'octaèdre en feuilles planes. C'est la catégorie angulaire 1 des solides de Platon. - L'ouverture des cônes provient de la théorie quantique de la précession des spins.

Fig.16. Tout en papier. Le dodécaèdre en 12 cônes, l'icosaèdre en 20 pyramides. Le dodécaèdre et l'icosaèdre en feuilles planes. C'est la catégorie angulaire 2 des solides de Platon. - L'ouverture des cônes et celle des pyramides proviennent de la théorie quantique de la précession des spins.
30
GQ2sur2 GQ1sur2 http://www.lisulf.quebec/GQ1sur2
EquipartitionSphere http://www.lisulf.quebec/EquiSpherehtml Atomesentetrades http://www.lisulf.quebec/Atomesentetradeshtml PrecessionSpin http://www.lisulf.quebec/PrecessionSpinhtml Quebecium http://www.lisulf.quebec/quebecium.qc.ca
Traduction interdite Tous droits de traduction réservés