GQRBDtxW5.1
QuantaPlaton, EquipartitionSphere, Atomesentetrades, PrecessionSpin, Géométrie quantique : pour le tout voyez Québécium
Traduction interdite Tous droits de traduction réservés
Système du Québécium.
Géométrie quantique du rhombododécaèdre régulier
Les familles de rhombododécaèdres isoédriques, les solides étoilés
Pierre Demers
Génération du rhombododécaèdre régulier par les cônes de précession d'un spin
Nous avons montré récemment comment les cônes de précession de la théorie quantique de l'atome peuvent générer les 5 polyèdres réguliers de Platon. Nous allons voir ici qu'ils peuvent aussi générer un 6e solide, le rhombododécaèdre régulier.
Le rhombododécaèdre régulier (RBD)
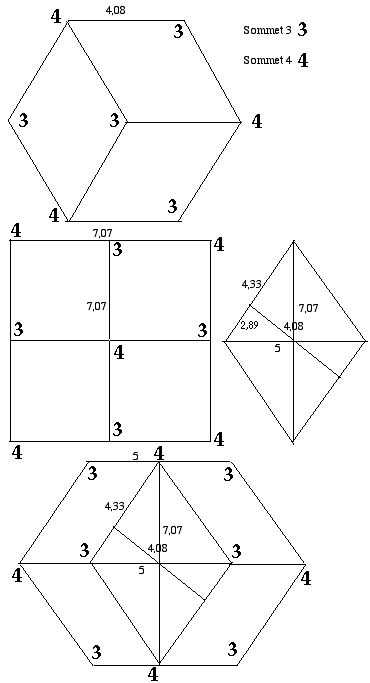
Ce solide a 12 faces égales losanges, dont les diagonales sont entre elles dans le rapport de 1 à Ã2 (racine carrée de 2 = 1,4142...). Voici ses aspects. Fig. 1. Les angles dièdres sont égaux et valent 120o, il a 24 arêtes, 6 sommets 4 et 6 sommets 3. Il est le dual d'un solide d'Archimède, le cuboctaèdre. Voici le losange des faces du RBD régulier, qui est caractérisé par son petit angle valant 70,53o : c'est le losange 70,53o. Fig. 2
Nous retrouvons l'angle 70,53o, supplément de 109,47o et angle dièdre du tétraèdre régulier, dont nous avons signalé l'universalité. http://www.lisulf.quebec/PrecessionSpinhtml

Fig. 1. Trois vues du RBD régulier. Vue d'une face. On peut le considérer comme formé de 3 chaînes entrecroisées de 4 faces losanges, ces faces dessinant un carré (vue centrale où 4 faces apparaissent par la tranche.).
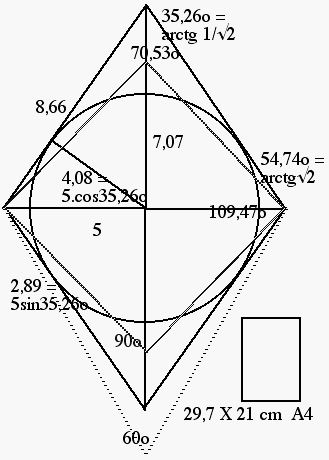
Fig. 2. Une face du RBD régulier. Le losange de petit angle 70,53o. Dans le papier A4, où les dimensions sont dans le rapport 1/Ã2, on taille à vue 4 losanges ayant les mêmes proportions, de grande diagonale 14,85 cm.
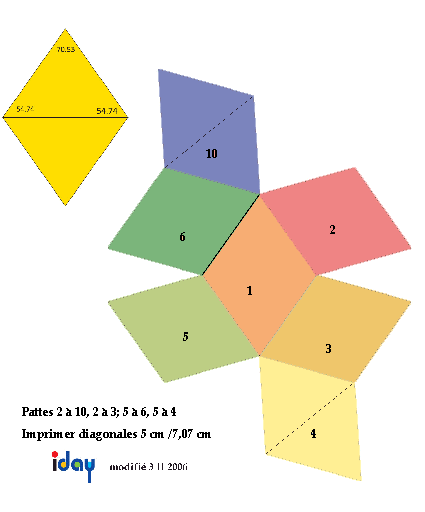
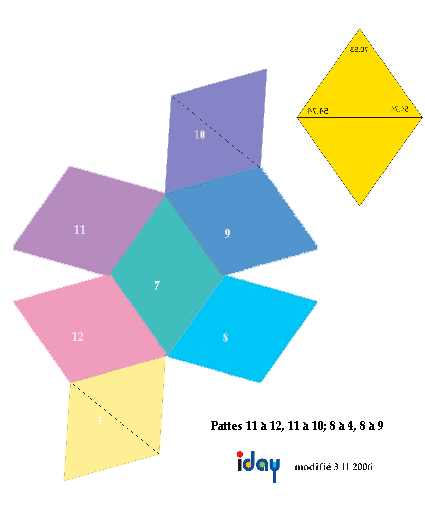
Figs 3 et 3 bis. Plan et patron des faces du RBD régulier. On le fabrique commodément en 2 coques de 7 faces qui s'assemblent. Couleurs distinctives de Maurice Day suite normale, réf. Fibonacci.
On obtient le RBD régulier par l'assemblage de 12 losanges 70,53o, selon un plan figs 3 et 3bis. On peut aussi assembler 12 pyramides constituantes ayant pour base un losange 70,53o servant de face et comme hauteur la moitié de la grande diagonale de ce losange, réunies en leurs sommets. Fig. 4.
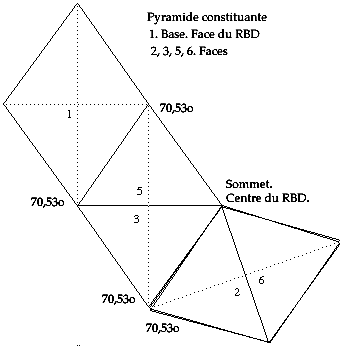
Fig. 4. Patron de la pyramide constituante.

Fig. 5. Plan de la pyramide constituante.
Voyez le résultat Fig. 16.
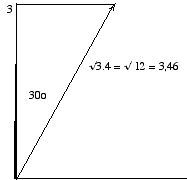
Fig. 6. Le spin 3 projection 3.
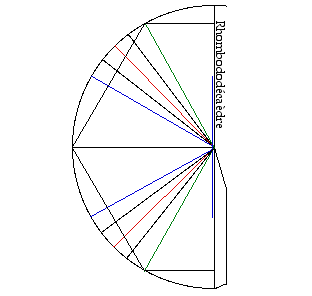
Fig. 7. Patron du cône d'ouverture 2thêta = 60o de précession du spin 3/3.
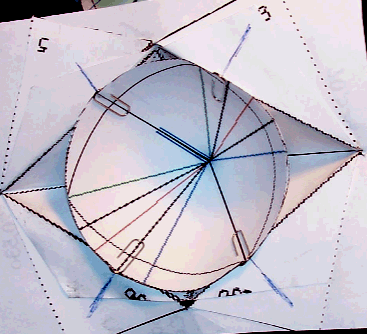

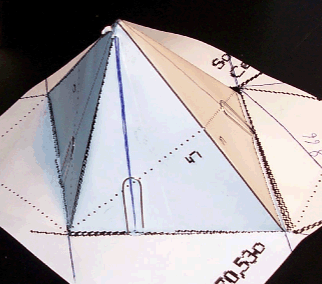

Fig. 8. Ajustement d'un cône de précession et d'une pyramide constituante. Quatre génératrices du cône sont tangentes à la pyramide. Vues b, c, d, e.
Génération par les cônes de précession du spin 3
Le RBD régulier est généré par association directe par le cône d'ouverture 60o appartenant au spin 3 projection 3. On prend 12 de cescônes. Les bases circulaires de ces cônes déterminent des losanges circonscrits des proportions voulues. Les cônes sont assemblés avec une origine commune. Chacun partage une génératrice avec 4 autres. Le patron des cônes est d'une simplicité remarquable : c'est un demi-cercle.
Spin 3 projection 3. Angle du cône de précession thêta. costhêta = 3/Ã(3.4) = Ã(9/12) = Ã(3/4) = 0,8660 = cos 30o.
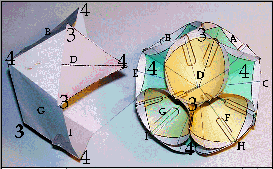
Fig.9. Rhombododécaèdre régulier en 7 feuilles de papier (7 faces sur 12) à gauche; et en 12 cônes à droite. Lettres A ... I : les faces et les bases des cônes. Chiffres : les sommets 3 et les sommets 4. Trombones : les génératrices pairées, communes à 2 cônes.

Fig. 10. Comme figure 9. La génératrice mesure 10 cm.

Fig.11. Comme il est bien connu, six cercles se logent facilement en couronne autour d'un seul, de même, six perles sphériques (V vertes) autour d'une seule, en déterminant un axe de symétrie (vertical) et un centre de figure. Passant à trois dimensions, on peut placer 3 autres perles (J jaunes) d'une seule manière et 3 autres encore (R rouges) de deux manières soit en alignement avec les 3 précédentes, soit en alternance. La manière alignement établit 3 plans de symétrie contenant la verticale et passant chacun par une perle R et une J. La manière alternance établit un centre de symétrie, chaque perle ayant son opposé symétrique par rapport à ce centre. On montre ici l'alternance, qui s'accorde avec la manière des cônes qui génèrent le RBD régulier. La manière alignement ne conduit pas à générer le RBD régulier.
Nota-bene. Principe d'incertitude.
Concernant le RBD régulier. Cet angle thêta et la forme géométrique qui en découle sont définis exactement sans approximation aucune qui résulterait d'une mesure. Ils sont des constantes de la nature aussi bien que le nombre pi et échappent au principe d'incertitude de Heisenberg. Ils dépendent des hypothèses à la base de la théorie quantique de l'atome.
En d'autres termes. On aperçoit une quantité qui est totalement indéterminée : la position angulaire phi du vecteur I dans sa rotation autour de l'axe Oz. Dans nos conditions de mesure idéale, on a
delta phi = infini
et cette équation d'imprécision totale a sa contrepartie d'une erreur nulle sur l'angle thêta
delta thêta = 0.
thêta et phi apparaissent comme si elles étaient des variables quantiques conjuguées, avec l'équation d'incertitude et la valeur de h/2pi
delta phi X delta thêta >= h/2pi
Des considérations semblables s'appliquent évidemment à la géométrie quantique des 5 solides platoniciens étudiés précédemment. Chaque fois, la relation angulaire établie avec les cônes de précession s'applique avec exactitude et sans approximation.
Les plans colorés du RBD régulier
Les faces opposées ont des numéros différant de 6 et en principe des couleurs contraires. Les choix colorés possibles sont multiples, ceux utilisés ici sont dus à la collaboration de Maurice Day.
Une famille continue de rhombododécaèdres isoédriques
Caractérisons le losange du RBD régulier par son angle 70,53o et regardons cet angle comme un paramètre pouvant varier. De petites variations de ce paramètre ne nous empêchent pas d'obtenir un solide ayant 12 faces égales losanges. On peut adopter par exemple 72o, angle cinquième de cercle, qui donne effectivement un patron réalisable et commode à tracer. Il existe par suite un domaine angulaire comprenant 72o, conduisant à une famille de RBD isoédriques c'est-à-dire à faces égales. Il reste à établir ses limites. On aperçoit facilement les limites 60o et 90o, mais il est possible que le domaine réel soit plus resserré.
60o < paramètre < 90o
On montre le patron d'un RBD dont les faces sont des losanges 72o cinquième de tour, qui est effectivement réalisable, confirmant la dernière inéquation. Fig. 12
paramètre 2pi/5 = 72o
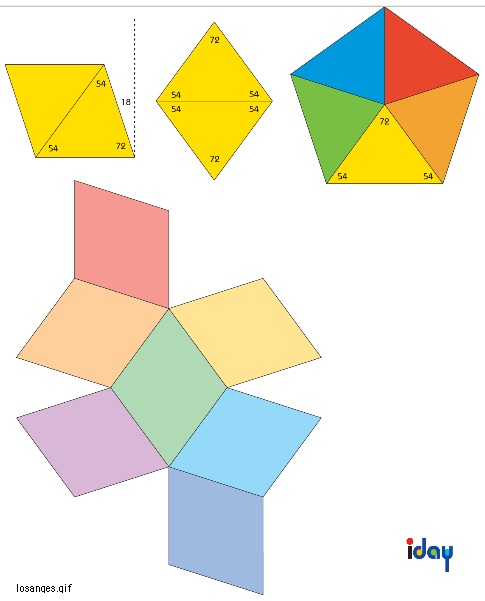
Fig. 12 Losanges 72o et patron d'un RBD isoédrique.
La correspondance avec le spin 3/3 n'est démontrée que lorsque les angles dièdres valent 120o, comme c'est le cas pour le RBD régulier découlant du paramètre losange valant 70,53o. Pour les autres valeurs du paramètre, les angles dièdres restent à établir.
Le (pseudo-) rhombododécaèdre de Fibonacci
La série et le nombre de Fibonacci ont acquis une importance en art et en biomathématique. Le nombre de Fibonacci vaut 1,618..., pas tellement différent de Ã2 = 1,414. On peut adopter ce nombre pour tracer des losanges de Fibonacci, dont le paramètre losange vaudra 58,283o et essayer d'obtenir un dodécaèdre avec ces losanges. L'expérience organisée par Maurice Day a donné deux résultats intéressants.

Fig. 13. Douze losanges de paramètre 58,53o, Ils s'assemblent en donnant un RBD de Fibonacci avec explications, les explications signalant qu'il apparaît 24 faces triangulaires, les losanges se pliant en deux selon la grande ou la petite diagonale. Les couleurs offrent une série normale avantageuse.
Primo. Il y a confirmation de l'inégalité du paragraphe précédent, le losange de Fibonacci est hors limites. On obtient une figure 3D apparemment à 12 faces mais des empêchements stériques font que les losanges de papier ne restent pas plans : ils se déforment par cintrage et pliage.
Secundo. On peut obtenir un solide figure formée de triangles plans exacts, chaque losange se pliant au choix selon la petite ou la grande diagonale. Cette figure pourrait s'appeler rhombododécaèdre de Fibonacci avec explications. Cette désignation couvre une famille en nombre grand mais limité de solides à 24 faces selon les pliages, nombre calculable par la combinatoire.
De plus, on peut sans doute choisir pour le paramètre des valeurs peu différntes de 58,28o et obtenir encore un solide apparemment à 12 faces et réellement à 24 faces. Il existe par suite une famille infinie de familles avec explications du même type que celle de Fibonacci, ayant 24 faces.
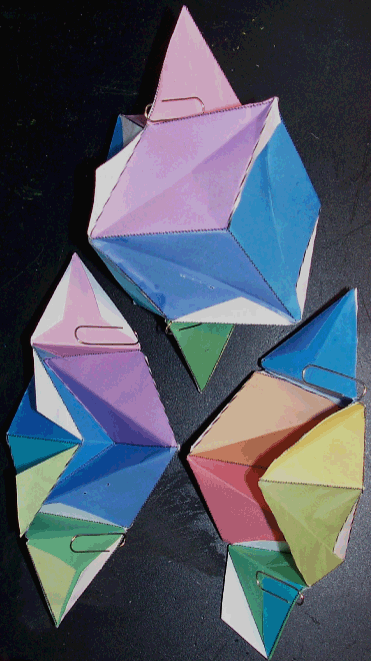
Fig. 13ter. (Pseudo)-rhombododécaèdre de Fibonacci et ses deux coques.
Le rhombododécaèdre régulier étoilé
Comme il est connu, le rhombodécaèdre régulier RBD se prête à l'addition de 12 pyramides de base losange, une sur chacune de ses 12 faces, résultant du prolongement de ses 12 faces et de ses 24 arêtes. Chaque face losange donne naissance à 4 faces triangulaires toutes semblables. Le résultat est un solide étoilé ayant 48 faces et 24 arêtes. Les angles dièdres sont tous égaux à 120o ou à son supplément. Il y a 12 sommets 4 (rencontre de 4 arêtes) pointus vers l'extérieur et 14 sommets 6. Voici le patron d'une pyramide. Fig. 14.
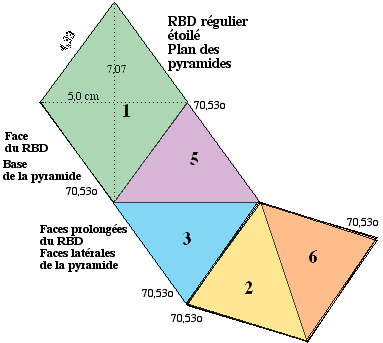
Fig. 14. Une des 12 pyramides d'addition (face 1), permettant d'obtenir un RBD étoilé. Elles différent entre elles par les Nos et les couleurs de leurs faces.
Les faces triangulaires des pyramides sont coloriées selon la couleur des faces losanges qu'elles prolongent. Il y a autant de plans colorés que de pyramides, chacune d'elles ayant 5 faces et 5 couleurs, dont 4 visibles : au total 12 plans colorés. Chaque couleur s'aperçoit sur 4 portions triangulaires de plans. Voici le schéma des couleurs, couleurs de 1 à 12. Le premier nombre appartient à la base invisible, face du RBD, les autres nombres, aux 4 faces prolongées ayant une arêtes commune avec la face cachée. Sens de rotation des aiguilles d'une montre.
Il y a 12 fichiers .
Pyram.......Le schéma coloré dans les figures 3 et 3bis .
1er...2e...3e.....4e.....5e
1
......2......3......5......62
......10......11......3......13
......1......2......12......44
......3......12......8......55
......6......1......4......86
......1......5......9......107
......9......8......12......118
......5......4......7......99
......8......7......10......610
......11......2......6......911
......2......10......7......1212
......4......3......11......7Voici le patron d'une pyramide d'addition. Fig. 14. Les pyramides d'addition et les pyramides constituantes ont exactement la même forme. Dans le RBD étoilé, elles se présentent par paires opposées par la base, formant une bipyramide. Voyez l'aspect du RBD régulier étoilé. Fig. 15
Les RBD de la famille isoédrique ont eux aussi chacun une forme étoilée et il y a quelque chose de semblable pour chacun des pseudo-RBD de Fibonacci.

Fig. 15. Le rhombododécaèdre régulier étoilé.
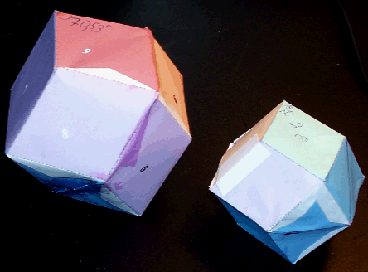
Fig. 16. Le RBD régulier, paramètre losange 70,53o; un RBD de la famille RBD isoédrique, paramètre losange 74o.
Géométrie quantique des solides étoilés
On peut dire que la géométrie du RBD étoilé est contenue dans celle du RBD, dans ce sens que le passage à la forme étoilée se fait sans introduction de valeurs nouvelles d'angles. L'opération de passage consiste dans le prolongement de droites et de surfaces planes. Les angles dièdres restent les mêmes. On peut dire que la géométrie quantique du RBD étoilé elle aussi se trouve contenue celle du RBD. Une fois le RBD généré à partir d'un cône et d'un spin, il n'y a pas à chercher l'intervention d'un cône et d'un spin supplémentaires.
Il semble légitime de
généraliser ces
observations aux autres solides
étoilés, en premier lieu,
au petit dodécaèdre
étoilé.
Association indirecte et
facteur 2
Dans la génération du dodécaèdre par association indirecte, un facteur 2 est nécesaire pour concilier théorie et réalité. L'angle théorique est 126,870o et le supplément del'angle dièdre réel est 63,435o. À ce propos, remarquons qu'un facteur 2 se rencontre dans la bipyramide et dans le bicône correspondant qu'il s'agisse du RBD étudié ci-dessus, ou du dodécaèdre étudié précédemment. On passe de l'angle simple à l'angle double et inversement par une opération charnière, et de telles opérations ont une vogue certaine chez les géomètres des solides.
Voyez Association indirecte in. http://www.lisulf.quebec/GQ1sur2
Voyez le cube de Yoshimoto. http://www.ac-noumea.nc/maths/amc/polyhedr/Yoshimoto.htm
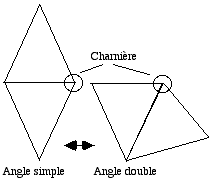
Fig. 17. Bipyramide ou bicône. Opposé ou côte-à-côte. Par une opération charnière, l'angle occupé varie d'un facteur 2.

Fig. 18. Pyramides et une bipyramide du RBD. Position opposé.

Fig. 19. Bipyramide et bicône du dodécaèdre. Positions opposé et côte-à-côte.
Fig 20.
Deuxième patron de la pyramide
RBD.
Fig. 21. Patron de la
pyramide régulière
à base carrée. (Pyramide
NY).
Fig. 22. Pyramides et
bipyramides RBD et NY. Les bipyramides
sont congruentes entre elles, mais les
pyramides ne le sont pas.. Nouméa et
Yoshimoto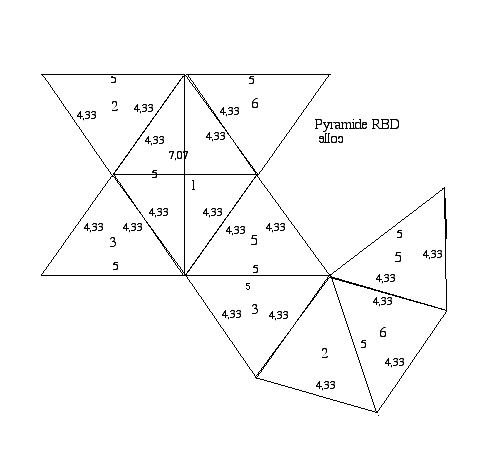


On trouve dans ces références une richesse de modèles charnières avec animation. La "modeste pyramide régulière de départ" que nous appelons NY possède une affinité avec la pyramide constituante et la pyramide coiffante ci-dessus. Elle a pour base un carré et pour hauteur la moitié du côté c de ce carré, pour arêtes obliques cĂ3/2 = 0,866 c, pour grandes diagonales cĂ2 = 1,414 c.
Prise 2 fois, elle donne une bipyramide NY de hauteur égale au côté du carré qui est congruente à notre bipyramideRBD. Mais les pyramides NY et RBD ne sont pas congruentes.
GQRBDtxW5.1
QuantaPlaton, EquipartitionSphere, Atomesentetrades, PrecessionSpin, Géométrie quantique : pour le tout voyez Québécium
Traduction interdite Tous droits de traduction réservés
30