GQSVtx
QuantaPlaton EquipartitionSphere Atomesentetrades PrecessionSpin RBD : voyez Quebecium
Traduction interdite Tous droits de traduction réservés
Système du Québécium
Géométrie des solides sans volume
Pierre Demers
Une annexe à la géométrie quantique
La géométrie quantique, créée dans le cadre du système du québécium, suggère d'explorer, au bénéfice de la physique et des mathématiques, la théorie des solides de Platon et autres, au-delà des nouveautés que nous avons mises en évidence précédemment. Les présentes remarques sont purement géométriques
Des solides dérivés
Stellation. Certains solides se prêtent à l'obtention de solides nouveaux par le prolongement de leurs faces, sans introduction d'angles nouveaux entre les faces. Entre autres, on note 2 solides de Platon : le dodécaèdre et l'icosaèdre réguliers, puis le rhombododécaèdre régulier et plusieurs autres. Le résultat est un solide étoilé, le processus (aussi bien que le résultat) est une stellation. Dans une stellation, les angles dièdres à la rencontre de deux faces sont préservés.
Une stellation augmente le volume le volume du solide initial.
Translation. Tous les solides se prêtent à l'obtention de figures nouvelles par translation des faces. Le cas général comprend la translation d'une face dans son plan, la figure résultante n'est plus fermée et cesse d'être un solide. Excluons de tels cas et convenons de nous restreindre aux translations d'une face selon la droite joignant son centre au centre du solide, en préservant la forme et la grandeur de toutes les faces. On peut procéder à des translations sur plus d'une face. Appelons précisément translation le processus et le résultat. Le résultat est une collection de surfaces planes et peut comprendre un solide.
Ces translations réduisent le volume du solide initial.
Certaines translations sont banales, par exemple le raccourcissement d'un madrier, parallélipipède ou cube avant comme après.
Nous pouvons encore convenir que la translation se fera à l'échelle, c'est-à-dire qu'il affectera toutes les faces d'un solide donné simultanément de manière à préserver la forme du solide initial. À chaque instant au cours de la translation, nous avons un solide augmenté de surfaces prolongeant ses faces.
Solides translatés. Enfin, nous ajoutons cette convention que toutes les faces seront déplacées jusqu'à contenir le point centre O du solide initial. À ce moment, si les n faces du solide initial étaient toutes parallèles 2 à 2, elles se confondent 2 à 2 dans le résultat, qui ne comprend que n/2 surfaces. À la limite du processus, le solide résultant a un volume nul. Il ne possède plus d'éléments tridimensionnels, mais les éléments qu'il possède occupent 3 dimensions.
Les translations décrites sont centripètes. De plus, elles sont virtuelles, puisqu'elles exigent que les faces s'entrecroisent. Dans le résultat, les faces sont morcelées.
Nous conviendrons de réserver les termes translation d'un solide et solide translaté au processus décrit aboutissant à une collection de surfaces incluant un volume zéro. Il n'y a pas tout à fait une contradiction : notre point de départ est bien un solide, qui possède un volume, fermé de toutes parts par des plans, et ce n'est qu'une fois translaté, qu'il n'en possède aucun.
Analogies verbales : un réservoir est ce qui renferme de l'eau; un réservoir une fois vidangé n'en renferme pas. Une bouteille de bon vin une fois bue est plus qu'un souvenir: elle est un objet ayant son encombrement tridimensionnel. Vidange et libations sont les analogues de nos translations.
Représentation zénithale
L'ensemble des plans parallèles à l'horizontale est caractérisé par un zénith commun et un nadir commun. De même, un plan d'orientation arbitraire appartient à un ensemble de plans qui lui sont parallèles, que nous appellerons horizon. Un horizon est caractérisé par un point que nous appellerons zénith, sur la sphère des angles solides ou des coordonnées sphériques, et son antipode.
Les faces d'un solide ont chacune un horizon et un zénith. Pour les caractériser complètement, il faut encore donner la forme de leur pourtour et les coordonnées xyz de leur centre. Deux faces parallèles diffèrent par xyz. : on change tous les signes
La translation appliquée à un solide préserve les caractéristiques ci-dessus de chaque face sauf les coordonnées de son centre, qui deviennent uniformément 000. Les coordonnées zénithales sont utiles pour comprendre les dièdres formés par les faces du solide translaté. Les dièdres s'articulent autour d'une droite à angle droit sur la sphère, par rapport aux zéniths des deux faces considérées. Un trièdre est formé par un trinôme de points zénithaux et détermine un cornet ou cellule ouverte de trois surfaes planes ayant un sommet commun au point O.
Un solide de n faces a 2n zéniths y compris les antipodes. Si ses faces sont parallèles 2 à 2, le nombre est n.
Question. Étant donné n points sur une sphère, combien de trinômes élémentaires, c'est-à-dire n'incluant pas un autre point, peut-on y reconnaître? C'est un problème de topologie; a-t'il été posé et résolu dans sa généralité? Si un lecteur veut bien m'adresser la solution, je lui en serai reconnaissant.

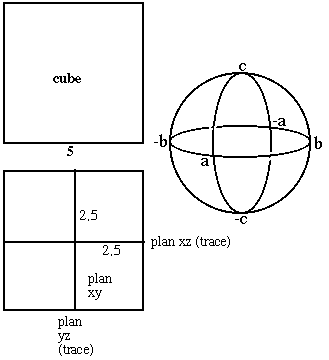
Fig. 1. Un cube et le cube sans volume correspondant comportant 3 carrés disposés en trièdre trirectangle. On reconnaît 8 cellules triédriques. - Dans la sphère des angles solides, les 6 points représentant les 6 faces du cube, translaté ou non.Il est facile d'y reconnaître les 8 cellules.
Un cube sans volume
Chaque face garde ses dimensions et ses angles plans et son zénith. Nous la déplaçons d'un mouvement rectiligne en amenant son centre au centre de figure du solide donné. Examinons l'effet de rapprocher les faces horizontales. L'épaisseur décroît et atteint, à la limite, zéro. Semblablement pour les faces verticales. Les faces gardent leurs dimensions planes mais perdent, à la limite, leurs distances. Le résultat est une collection de 3 carrés trirectangles et de 8 cellules triédriques ayant chacune 3 faces et un volume nul. L'encombrement ou volume occupé reste le même, il n'a pas changé.
Dans le cas du cube, les 6 faces occupent 6 plans distincts ABCDEF, les plans parallèles se ramenant à un seul, il suffit d'écrire ABC. Les binômes sont ab, ac, bc, ce sont les 3 axes trirectangles. Les trinômes sont au nombre de 8 : abc, ab-c, a-bc, a-b-c, -abc, -ab-c, -a-bc, -a-b-c. Ils déterminent 8 cellules trirectangles.
Aspect topologie : 6 points sur la sphère conduisent à 8 triplets élémentaires.
Un tétraèdre régulier sans volume
Les 4 faces n'ont pas de parallèles opposées, il y a donc 8 points y compris les antipodes : ±a, ±b, ±c, ±d.
Un rhombododécaèdre régulier (RBD) sans volume
Le RBD a 12 faces qui se ramènent à 6 pour cause de parallélisme et par suite il y a 12 points sur la sphère des angles solides, qui sont sont ±a, ±b, ±c, ±d, ±e, ±f.. L'analyse a été réalisée sur modèle. Figs 2 à 5. Réf. Fig. 11 de GQRBDtxW5.1.html
http://www.lisulf.quebec/GQRBDtxW5.1.html
Le RBD sans volume a 24 cellules en 12 nacelles.
Aspect topologie : 12 points sur la sphère conduisent à 24 triplets élémentaires, chacun à l'origine d'une cellule.
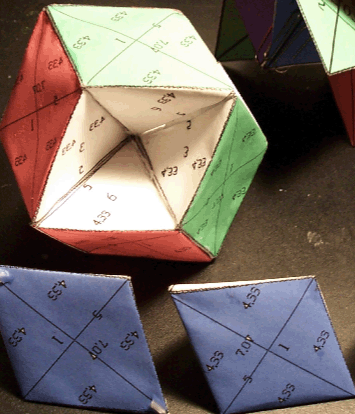
Fig. 2. RBD régulier. Le code couleur est trichrome RVB. Quatre faces de chaque couleur forment une chaîne continue, les trois chaînes s'entrecroisent .La chaîne B n'est pas en place.
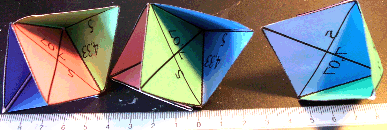
Fig. 3. Les 24 cellules se présentent par paires, formant une sorte de petit bateau avec voilure ou de nacelle. Chaque nacelle bicellulaire est trichrome, sa voilure est monochrome.

Fig. 4. Un RBD sans volume. Une paire de faces parallèle (B pour bleu) du RBD, après translation, devient une portion de plan passant par le centre de la figure. Cette portion de plan est un losange fragmenté par les intersections, en 2 grands losanges et 4 petits triangles. Les losanges sont les voilures et les triangles sont la coque des nacelles.
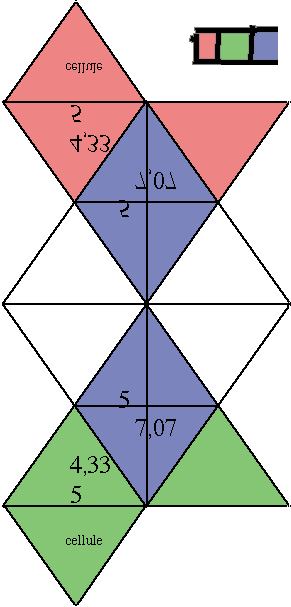
Fig. 5. Patron de la nacelle bicellulaire RBD. Ici, voilure B, coque R et V.
Propriétés des solides sans volume
Translation inversée. Éclatement. Pour obtenir le solide translaté à partir du solide initial, on a fait suivre à chaque face du solide un parcours centripète. Pour retrouver le solide initial à partir du solide translaté, il suffit de procéder au parcours centrifuge correspondant sur chacune des faces translatées. Si une face translatée résulte de 2 faces initiales, il faut lui appliquer 2 déplacements en sens opposés. Ce processus a une analogie dans l'éclatement en dessin architectural et industriel. Cependant, dans le dessin éclaté, les éléments déplacés sont des objets 3D et non de simples surfaces planes sans épaisseur.
Restitution. Une propriété est de restituer le solide initial par un petit nombre d'opérations simples sur chaque cellule.
Dans le cas du cube sans volume, il faut ajouter à chaque cellule 3 faces carrées de dimensions linéaires 50% des carrés faces du cube original, selon chacun des 3 horizons et on retrouve le cube initial à la même échelle, 100%. Sur les 8 cellules, le total est 24 carrés.
Dans le cas du RBD sans volume, on tourne le grand losange monochrome de chaque nacelle, de 90o autour de son petit axe. De la sorte, il vient fermer la nacelle et la transforme en une pyramide constituante et ce, pour chacune des 12 faces. On obtient un RBD semblable à l'original mais à l'échelle linéaire 50%. La différence d'échelle vient de ce que, dans l'opération proposée, on a laissé de côté les petits triangles des nacelles, qui représentent la moitié de la surface du solide initial.
On peut encore dire : on tourne la voilure autour de sa petite diagonale et elle devient le pont du petit bateau.
Autre. Dans le cas du RBD , on obtient en une seule étape un RBD étoilé. Il suffit de tourner chaque nacelle à l'envers autour de son grand axe. Le résultat est semblable au RBD initial que l'on coifferait, mais à l'échelle 50%.

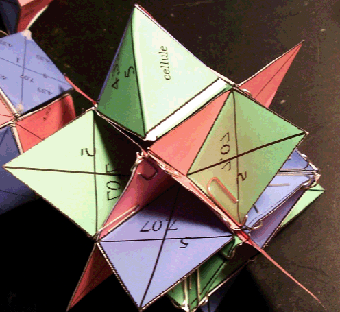
Fig. 6. Dans une nacelle-petit bateau, la voilure a été tournée de 90o autour du petit axe du losange, donnant un pont au petit bateau et une face au RBD en cours de restitution.- Une nacelle a été tournée sens dessus - dessousautour de son grand axe et on a obtenu une face coiffée; toutes les faces étant coiffées, on aura un RBD étoilé.
GQSVtx
QuantaPlaton EquipartitionSphere Atomesentetrades PrecessionSpin RBD : voyez Quebecium
Traduction interdite Tous droits de traduction réservés
Traduction interdite Tous droits de traduction réservés
30