GravitationQuantification

Systême du Québécium:

http://lisulf.quebec/quebecium.htm

Système du Québécium.

Gravitation et quantification.

Pierre Demers, 6III2015

Version du 17III2015.

Traduction interdite.

Poser le problème, pertinence du cadre de réflexion.

Le Modèle Standard n'inclut ni la gravitation ni la relativité, choses restant mystérieuses, même s'il est couramment admis que la gravitation est associée à la relativité généralisée et à une déformation de l'espace-temps. Par ailleurs, il n'existe aucune théorie sur les masses des particules. Or il n'existe de forces gravitationnelles qu'entre objets matériels dans l'univers formés de particules ayant une masse et une masse au repos non nulle. On imagine mal que des forces gravitationnelles pourraient s'exercer entre des neutrinos ou des photons au repos.

Dans une telle perspective, on peut penser que l'analyse des masses des particules pesantes - appelons les particules graves, pourrait conduire à cerner le problème posé.

C'est pourquoi je rassemble ici des résultats démontrant des régularités dans les masses des particules subatomiques ou quasi-subatomiques datant de près d'un quart de siècle. Depuis ce temps, j'ai appris l'importance du nombre magique 30 et celle de la géométrie dans la compréhension des atomes.

Nombres magiques.

Ces résultats démontrent l'intervention de nombres magiques:

2 puissance -1/2 ce qui est relié aux angles solides

et 2 puissance 1/12 = 1,059.463 ce qui est relié au demi-ton de la gamme diatonique musicale.

Voyez dans les Annexes 1 à 4.

Annexes.

Je reproduis les textes sans altération.

============================

Ann. 1. http://www.er.uqam.ca/nobel/c3410/4eforceter.html

4eforce

Rev. Biomath. 116, 5-11, 4e trimestre 1991

LA 4E FORCE, UNIFICATRICE DES FREQUENCES EXTREMES

Pierre Demers,

Centre québécois de la Couleur,

1200, rue Latour, Saint-Laurent (Québec) H4L 4S4

Communication présentée au XIIIe congrès international de biomathématique, le 6 septembre 1991. Kremlin-Bicêtre (France)

Résumé. L'analyse biomathématique des fréquences de de Broglie pour les particules chargées les plus stables montre des régularités qui paraissent s'expliquer par une quantification de la 4e force, force gravitationnelle.

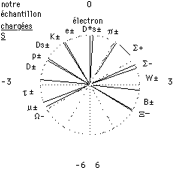
Fig. 1. Cette figure montre une gamme où l'électron est un la et le proton est un sol. Elle manifeste des régularités touchant toutes les catégories de particules élémentaires: des leptons, des bosons de jauge chargés, des hadrons (des mésons et des baryons). Le principe de cette synthèse paraît être la quantification de la 4e force, laquelle expliquerait ainsi les masses des particules élémentaires aussi bien que les mouvements des astres.

Lois biomathématiques musicales

Des travaux de Joël Sternheimer (1)(2) ont établi que les particules élémentaires suivent des lois musicales dans la distribution de leurs masses, proportionnelles à des fréquences, selon la relation fondamentale de de Broglie qui s'écrit comme suit, avec M masse en unités égales à la masse de l'électron me±, m masse en Mev, et f en Hz.

f = 0,209.3 M 2⁶⁹ = 0,409.62 m 2⁶⁹

f = 428,7 M 2⁵⁸

Ces travaux s'accordent avec un modèle biomathématique de l'auteur, proposant que des relations mathématiques semblables unissent toutes les perceptions humaines : couleur, audition, relativité et particules matérielles.(3) En collaboration avec Longavesne, l'auteur a confirmé et étendu les conclusions de Sternheimer.(4)(5)

Lois de gamme et d'octave

L'auteur a obtenu des résultats nouveaux pour un échantillon privilégié de particules élémentaires. Cet échantillon contient 15 particules chargées classées comme stables S dans les tables. Il existe 19 particules chargées S, mais nous avons exclu les 4 baryons les plus lourds, qui sont charmés et qui donnent des résultats discordants.(6)(7)

Cet échantillon manifeste des régularités remarquables lorsqu'on examine les hauteurs X et x, logarithmes des masses. Cela revient à placer ces masses selon une progression géométrique. On utilise la base 2 et la base b = 1,059.463 = 2^1/12. Le nombre 2 détermine l'intervalle de l'octave, le nombre b, celui du degré diatonique. Il y a 12 degrés diatoniques dans la gamme tempérée.

X = log₂M x = log_bM

Les résultats principaux peuvent se décrire ainsi.

1. Il y a une "règle d'octave", selon laquelle X n'aurait que des valeurs entières. Cette règle n'est pas respectée exactement. Appelons D X la différence entre X et l'entier le plus proche K, appelé N° d'octave.

D X = X-K K = ent(X+0,5)

On constate que les valeurs de D X restent comprises entre -0,323 et +0,337 alors que, par construction, elles pourraient s'étendre entre -0,5 et +0,5. De plus, on trouve que la moyenne de D X pour les particules plus lourdes que l'électron est sensiblement nulle. Elle vaut 0,005. La règle d'octave s'accorde remarquablement bien avec la moyenne des hauteurs expérimentales.

2. Il y a une "règle de gamme", selon laquelle les hauteurs x n'auraient que des valeurs entières. Cette règle n'est pas respectée exactement. Si elle était respectée, les hauteurs dans la gamme h = 12D X seraient des nombres entiers et les positions occupées dans la figure 1 seraient les positions horaires sur le cercle divisé en 12. En effet, dans ce mode de représentation circulaire, les 12 notes de la gamme occupent les mêmes positions que les 12 heures d'un cadran d'horloge.

Appelons D dissonance la différence entre h et l'entier le plus proche H.

D = h-H H = ent(12X+0,5)

On constate que les dissonances restent comprises entre -0,06 et 0,33 avec une moyenne algébrique de 0,116. Puisque les valeurs de D sont pour la plupart positives, il est facile de réduire leur moyenne arithmétique en déplaçant l'origine dans la figure 1 vers les valeurs positives. En la déplaçant de 0,11 unités, on trouve l'écart arithmétique moyen suivant. Cela revient à examiner le rapport m/m' des masses, y compris la masse de l'électron, à une masse fictive m' supérieure de 0,64 % à celle de l'électron. (m/m' au lieu de m/me±).

s arith = 0,55 %

En considérant les dissonances comme des écarts, s arith donne une mesure du désaccord entre les masses expérimentales et notre modèle musical.

La valeur précise de 2 est requise dans les équations. En remplaçant 2 par 2(1±1%), toute apparence de régularité disparaît dans la figure 1. On a procédé à un contrôle plus rigoureux en remplaçant 2 par 2(1+e ) et en cherchant si une valeur de e différente de zéro peut réduire l'écart arithmétique s arith trouvé ci-dessus égal à 0,55 % On obtient le minimum de s arith pour e = -0,000.7, c'est-à-dire que la valeur précise de 2 devrait être remplacée par 1,998.6, ou encore, qu'elle est confirmée à 0,07 % près. La valeur minimale de s arith est alors /

s arith = 0,54 %.

3. Les dissonances pourraient se comprendre par l'intervention des diverses gammes connues en musique, utilisant des rapports numériques autres que ceux de la gamme tempérée. Sternheimer a analysé les dissonances pour 38 particules et a reconnu qu'elles forment 6 classes qu'il a nommées A, B, C, D, E, F, qu'il explique par une synthèse des gammes d'Orient et d'Occident. Les particules de notre échantillon se rangent dans les classes D, E et F. Nous avons remarqué que les dissonances sont de préférence positives pour les particules chargées et négatives pour les particules neutres.

Symétries et prédictions

1. L'aspect régulier de la figure 1 invite à définir et à analyser les symétries intriguantes qu'elle contient. L'électron y occupe une position centrale, voisine du la du diapason; 9 positions horaires jointives H de -4 à 4 sont occupées, suggérant l'appellation de nonet. Ce nonet comprend les notes consécutives du fa au do#. Le ré, le ré# et le mi sont absents. Des règles d'exclusion semblent s'appliquer, entre autres pour les particules d'échange caractérisées : p ± occupe à elle seule une position horaire et il en est de même pour W±.

2. Par analogie avec l'effet Zeeman et avec l'isospin, il est possible de définir un vecteur isogamme H valant 4 unités et ayant 9 projections dans un espace abstrait des hauteurs H. Il donne ainsi les projections H = -4, -3, -2, -1, 0, 1, 2, 3 et 4. On peut alors parler d'un remplissage des octaves, analogue à celui auquel on procède dans le cas de la classification périodique des éléments. On trouve aussi bien qu'il y a 7 périodes, marquées par les N°s d'octaves K = 0, 8, 10, 11, 12, 13 et 17. K est l'analogue de n, nombre quantique principal. La dégénérescence énergétique dans une période donnée est levée par les projections de H, donnant des valeurs H de -4 à 4, assimilables à , s et j. Au total, il y aurait 63 places disponibles, seules 15 d'entre elles sont réalisées. On peut encore parler d'une structure fine associée à la dissonance D. Dans la figure 1, il n'y a pas deux niveaux ayant les mêmes nombres H et D. Il y a en définitive 3 nombres quantiques : K, H et D.

3. La constante de structure fine a dont l'inverse vaut 137,04 semble intervenir. Pour les particules plus lourdes que l'électron, la moyenne de K est 160/14 = 137,14/12. Toute somme autre que 160 donnerait une moyenne plus éloignée de 137,04/12; la moyenne de x est 137,20; la moyenne de x = ent(x+0,5) est 137,07

4. L'abondance des niveaux réalisés culmine au voisinage de x = 12X12 = 144. L'essence d'un modèle musical étant de reposer sur des nombres et des périodicités, il est naturel de considérer 137 et 144 comme importants pour toute extrapolation et toute répétition périodique. Une 2e accumulation de particules très lourdes (Higgs) pourrait ainsi se présenter aux environs de x = 274 et x = 288. Les masses seraient M = 7,5 à 16,8.106 ou m = 3,8 à 8,6 Tev.

5. Une analogie avec la couleur se présente. En effet, les pourpres, couleurs perceptuelles absentes du spectre énergétique des rayonnements visibles, complètent, à la manière des 3 notes absentes dans la figure 1, le cercle énergétique des couleurs.

La 4e force

Ce qui précède suffit peut-être à démontrer le caractère musical des particules de notre échantillon. Alors que la dualité vibration-masse, le plus souvent décrite comme dualité onde-corpuscule, apparaît comme essentielle à notre compréhension de la matière, aucune expérience, par le moyen de l'une de ces 3 forces : électromagnétique, faible ou forte, n'a pu mettre en évidence des vibrations sur des particules au repos.(8) Seule, semble-t-il, la mesure des masses, de leurs rapports et des hauteurs permet d'accéder à une telle évidence comme nous venons de le faire. Cette comparaison repose en principe sur l'usage de la balance c'est-à-dire qu'elle recourt à la 4e force, force gravitationnelle.

Il est par suite naturel de proposer que les lois de symétries et de régularités qui se révèlent ci-dessus résultent d'une quantification de la 4e force. Ce serait la 1ère manifestation expérimentale d'une telle quantification. Cette force explique les fréquences très basses des planètes. Elle expliquerait aussi les fréquences très élevées des particules élémentaires et, par suite, leurs masses. Elle interviendrait donc doublement pour expliquer l'Univers. Dès son début pour régir l'apparition des infiniment petits et, dans la suite, pour régir le comportement des infiniment grands formés par la réunion de ces infiniment petits.

Electricité, matière fondamentale

Les particules élémentaires neutres et les particules élémentaires chargées autres que celles de notre échantillon sont loin de montrer des régularités comparables à celles de la figure 1. Les particules de notre échantillon montrent une "musicalité" supérieure parmi les particules élémentaires. Cela permet de croire qu'elles seraient les véritables particules élémentaires.

D'après cela, la matière fondamentale serait électricité en même temps que masse et énergie. Les particules neutres résulteraient de l'union de deux particules fondamentales de signes opposés.

Références

1 Joël Sternheimer 1983, Musique des particules élémentaires, C. r., 297, II, 829-834

2 Joël Sternheimer 1986, Musique des particules élémentaires, Rev. Biomath., Nº 94 (88), 1-47

3 Pierre Demers 1983, Modèle biomathématique unitaire descriptif de toutes les perceptions humaines, Rev. biomath., Nº 81 : 13-58

4 Jean-Paul Longavesne et Pierre Demers 1986, texte, soumis à Interface de l'ACFAS

5 Jean-Paul Longavesne et Pierre Demers 1987, Ann. ACFAS, 55, 272

6 Pierre Demers 1991, communication soumise au 59ème Congrès ACFAS

7 Pierre Demers 1991, Fréquences de de Broglie et matière électrique, soumis à Ann. fond. L. de Broglie

8 Jozef Hurwic 1988, in Présence de Gaston Bachelard, réd. C. Atias et J. Le Moigne, Univ. Aix-Marseille III, 51-2.

... le concept de Louis de Broglie attribuant le caractère ondulatoire aux corpuscules matériels était à l'origine de la création par Erwin Schrödinger de la mécanique ondulatoire. Mais la théorie de Schrödinger est basée surtout sur les travaux du mathématicien irlandais William Rowan Hamilton... La fonction y de la mécanique ondulatoire est appelée fonction d'onde parce qu'elle rappelle par sa forme mathématique, et pour cette raison seulement, la fonction qui décrit la propagation d'une onde électro-magnétique. La seule représentation physique concerne le carré du module qui détermine la probabilité de présence du corpuscule considéré dans un endroit déterminé.

Nouvelle analyse NouvelleanalyseEc197.html --AccueilPierreDemers.html

============================

Ann. 2. http://www.er.uqam.ca/nobel/c3410/4eforceter.html

3e de 4 communications pour le XIVe congrès international de biologie mathématique.

Paris, 9, 10 et 11 septembre 1993.

Revue internationale de biomathématique, XXXII, 2e trimestre 1994, No 126, 35-46

Nouvelle analyse de l'échelle musicale

des particules fondamentales

Pierre Demers, Centre québécois de la Couleur

Résumé. On rappelle que la distribution des masses des particules fondamentales s'accorde sensiblement avec deux invariances d'échelle établissant un parallèle avec la théorie de la musique : 1o le facteur d'échelle est le nombre 2; 2o le facteur d'échelle est la racine douzième de 2, ègale à l'intervalle diatonique de la gamme musicale tempérée. 3o On examine dans quelle mesure l'adoption des intervalles musicaux utilisées dans d'autres gammes peut améliorer cet accord. 4o Cette invariance d'échelle signifie que les degrés de cette distribution sont proportionnels au logarithme des masses. Un parallèle se présente dès lors avec la théorie de l'information, dans laquelle le nombre de bits d'information est proportionnel au logarithme des probabilités. Dans la théorie statistique de la matière, les probabilités sont égales à un nombre de complexions parmi lesquelles un choix a été réalisé. On cherche à interpréter ce parallèle.

15 particules fondamentales

Ce travail continue celui qui fut présenté au XIIIe Congrès et publié dans notre Revue. L'analyse porte sur 15 particules qui apparaissent comme plus fondamentales que les autres et qui sont chargées électriquement. Par ordre des masses croissantes, elles vont de l'électron e± au boson de jauge W±. Deux particules de même masse sont comptées pour une seule si elles ne différant que par le signe de leur charge électrique, comme c'est le cas pour l'électron et le proton. Rappelons que Louis de Broglie, dans son premier travail, posa comme principe que chaque masse possède une énergie mc² selon la relation d'Einstein et une fréquence f selon la relation de Planck. (1)

f= mc²/h c célérité de la lumière, h constante de Planck

De la sorte, il est indifférent de parler des rapports mutuels des masses, des rapports mutuels des énergies ou des rapports mutuels des fréquences.

Si on évalue les masses en millions d'électron-volts Mev, voici la relation donnant numériquement la fréquence en hertz Hz.

f = 0,409.62 m 2⁶⁹ m en Mev

Si on fait apparaître la masse en unités valant la masse de l'électron soit 0,511 Mev :

f = 428,7 (m/0,511) 2⁵⁸ m en Mev

Au facteur 2⁵⁸ près représentant 58 octaves, la fréquence de l'électron est 428,7 Hz, voisine du la normal qui vaut 440 Hz.

Exemples d'invariances

La physique contemporaine doit beaucoup de ses progrès à la mise en oeuvre des notions de symétrie et d'invariance. On retrouve ces notions dans une foule d'exemples tirés des mathématiques élémentaires de la vie courante. L'exemple le plus immédiat peut être tiré de notre propre humanité. Dans l'opération de symétrie qui consiste à passer de l'un de nous à un autre, quelquee chose reste le même, c'est ce qui nous fait tous ressembler l'un à l'autre : le langage, une tête, deux bras, deux jambes, etc, en nous bornant aux caractères les plus évidents. Par ailleurs on note des différences de grosseur, de hauteur, de chevelure, et bien d'autres. L'invariance est à la fois véritable et incomplète. Entre l'aspect physique de tous les humains existent une différence d'échelle et en même temps une ressemblance ou ce que nous pouvons appeler une invariance d'échelle, elle aussi incomplète. Dans la structure du corps humain, il y a une symétrie entre la gauche et la droite, mais incomplète puisque le coeur est à gauche.

Considérons des triangles équilatéraux, qui sont des fictions oeuvres de notre imagination, et passons d'un tel triangle à un autre plus grand. Ils différent par leur côté mais c'est là leur seule différence : entre eux existe une rigoureuse invariance d'échelle.

Si l'on examine certains objets de l'art sériel tels que ceux du défunt Andy Warhol, on trouve un grand nombre de fois la représentation d'un même objet, mais pas tout à fait idenique à lui-même à chaue fois. C'est ce qu'on observe dans son célèbre "210 bouteilles de Coca-Cola", qui a rapporté 2,1 millions de dollars américains à leur propriétaire. L'opération de symétrie est le passage d'une case à l'autre, l'invariance est encore une fois véritable et incomplète. L'invariance est accompagnée d'une certaine diversité. Les chefs-d'oeuvre de l'architecture fournissent dans leurs structures des exemples de ces trois principes : symétrie, invariance et diversité.

La physique des particules a connu des progrès extraordinaires par l'exploitation de ces trois notions. La symétrie et l'invariance du groupe SU3 et d'autres groupes encore ont permis de prévoir l'existence et les propriétés plusieurs particules, mais elles sont imparfaites, et on parle alors de théories de jauge. Un très grand problème de symétrie imparfaite concerne l'abondance des protons positifs et des électrons négatifs. Comment expliquer l'absence apparente dans l'Univers d'une égale proportion de protons négatifs et des électrons positifs?

La musique présente un exemple particulièrement intéressant pour nous d'une invariance d'échelle. À tous les facteurs 2 exercés sur une fréquence audible donnée, on retrouve une perception musicale analogue : un do1 devient un do2. Un air transposé d'une quinte c'est-à-dire dont toutes les fréquences sont multipliées par un facteur voisin de 3/2, sonne pareil à nos oreilles. On dira qu'un son musical est invariant d'échelle sous l'opération de symétrie qui consiste dans ces transpositions, le facteur d'échelle étant tantôt le facteur 2 ou le facteur 3/2. Encore une fois, la symétrie est imparfaite et la transposition donne un résultat qui se discerne de l'original, la preuve étant que précisément on éprouve le besoin de transposer pour les fins de l'art.

La série des sons musicaux elle-même fournit un exemple d'invariance. Lorsqu'on passe d'une fréquence de cette série à la suivante, quelque chose reste constant et invariant : c'est la qualité d'appartenir à la collection des sons admis dans le cadre de la convention musicale, disons de la gamme choisie; les fréquences étrangères sont exclues, elles sont fausses. Et pour réaliser cette invariance, on trouve la foule des règles anciennes et modernes des tons, des semi-tons, des demi-tons, qu'ils soient majeurs ou mineurs, diésés ou bémolisés, doublés ou triplés ou bécarre, etc.

Une règle rigoureuse et universelle semble se maintenir à travers l'histoire de la musique : c'est la règle d'octave. Au bout de la gamme se trouve invariablement, c'est le cas de parler d'une invariance, l'octave de facteur 2. On peut assurément rattacher ce facteur 2 à des exigences de géométrie et de mécanique vibratoire. On pourrait philosopher sur l'importance de ce facteur 2 qui survient en musique et en physiologie et la rapprocher de ce qu'on vérifie en théorie de la gravitation et de l'électromagnétisme : la valeur exacte de 2 intervient dans les formules, comme puissance affectant les dimensions spatiales. Déjà Faraday l'avait vérifié pour la loi de l'inverse du carré de la distance en élevctricité, et toute la mécanique céleste repose sur l'exactitude de la puissance 2 dans la loi de l'attraction universelle. On peut assurément rattacher cela à des raisons d'angle solide donc de géométrie.

Quant à l'invariance d'échelle correspondant au respect du caractère musical quand on passe d'une note à une autre dans une gamme déterminée, une autre règle émergea il y a 300 ans et ce fut un perfectionnement décisif, qui facilita les transpositions et qui donna un essor nouveau à la polyphonie. C'est alors que Jean-Sébastien Bach (1685-1750) fit admettre que la gamme serait formée de douze demi-tons égaux emplissant l'octave, chacun est appelé demi-ton diatonique et la gamme est la gamme tempérée. Le demi-ton diatonique de la gamme chromatique vaut par suite un facteur b.

L'invariance d'échelle en musique concerne les fréquences. L'équidistance des octaves et celle des degrés de la gamme(do, do#, ré, etc) concerne le logarihme des fréquences. Si on fait usage du logarithme base 2, l'équidistance des octaves est d'une unité à la fois, l'équidistance des degrés de la gamme tempérée est d'un douzième d'unité ou 0,083.333. Si on fait usage du logarithme base b, l'équidistance des octaves est de douze unités et l'équidistance des degrés de la gamme tempérée est d'une unité.

L'invariance d'échelle se distingue de ce qu'on peut appeler l'invariance arithmétique. Ainsi un mur de briques égales, une page emplie de lignes équidistantes présente une sorte d'invariance ou de régularité, mais qui mérite l'épithète d'arithmétique : un rang, une ligne s'obtient à partir de l'élément précédent en ajoutant à ce dernier une hauteur additive. il y a progression arithmétique. Dans l'invariance d'échelle, il y a progression géométrique d'un degré au suivant, par l'application d'un facteur d'échelle, et les degrés deviennent égaux si l'on se sert de la fonction logarithme.

Première invariance d'échelle : le facteur 2

Voyons, dans le Tableau I, la description de nos 15 particules fondamentales.

Tableau I

Les particules fondamentales

(m/0,511), m masse, la masse de l'électron valant 0,511 Mev.

Classe Nom

3 leptons

électron e± (1)

muon µ± (206,77)

tau ± (3491,4)

1 boson de jauge

W± (157730)

11 hadrons

6 mésons

kaon K± (966,05)

pion π± (273,13)

D± (3658,1)

Ds± (3852,8)

Ds*± (4129,7)

beauté B± (10328)

5 baryons

proton p± (1836,15)

sigma ∑+ (2327,5)

sigma ∑- (2342,3)

xi X (2385,8)

oméga W (3272,9)

Ce sont là les particules chargées électriquement classées S (pour stables), en omettant les baryons charmés. Ces masses sont fort disparates, elles s'échelonnent entre 1 et 157730 et leur répartition, dans un premier examen, n'obéit à aucune régularité. Tout au plus peut-on remarquer une accumulation des masses au voisinage de celle du proton. Cependant, nous allons voir qu'une régularité apparaît dans cette distribution si nous examinons non les valeurs naturelles des masses mais leurs logarithmes. Nous utilisons le logarithme base 2, lequel vaut 3,321.928 fois le logarithme base 10. On reconnaît, au Tableau II, que les fréquences occupent 18 octaves. On rattache chaque valeur de X, égale à L₂(m/me±), au nombre entier le plus proche ou numéro d'octave K, qui reste compris entre 0 et 17.

X = L₂(m/me±)

K = entier(X + 0,5)

Tableau II. 15 particules fondamentales

logarithmes des masses : base 2 et base b = 2^1/12 = 1,059.463

Dans la colonne "octave", on a inscrit l'entier K le plus proche du nombre dans la colonne précédente

Nom	Mev	m/me±	X L2(m/me± )	K Octave	D X	Lb(m/me± )
e±	0,511	1	0	0	0	0
µ±	105,07	206,77	7,692	8	-	92,30
π±	139,568	273,13	8,093	8	+	97,12
K±	493,696	966,05	9,916	10	-	118,99
p±	938,27	1836,15	10,842	11	-	130,11
S +	1189,4	2327,5	11,185	11	+	134,22
S -	1197,4	2342,2	11,194	11	+	134,33
X -	1321,32	2385,8	11,337	11	+	136,04
W -	1672,43	3272,9	11,678	12	-	140,12
t ±	1784,1	3491,4	11,77	12	-	141,24
D±	1869,3	3658,1	11,837	12	-	142,04
Ds±	1968,8	3852,8	11,912	12	-	142,94
Ds*±	2110,3	4129,7	12,012	12	+	144,14
B±	5277,6	10328	13,334	13	+	160,01
W±	80600	157730	17,268	17	+	207,21

Par invariance d'échelle facteur 2, nous voulons ici dire que les masses rapportées à celle de l'électron seraient toutes égales aux puissances de 2. En d'autres termes, les valeurs de X seraient exclusivement des entiers. Le Tableau II fait apparaître, si on examine les colonnes X et K, des différences évidentes entre X et K (dont le signe seul figure dans la colonne D X = X - K).

Analysons ces différences D X = X- K. Sept d'entre elles sont positives et sept sont négatives, et la moyenne de leurs valeurs est 0,005, ce qui suggère soit qu'elles sont réparties au hasard soit que l'électron joue un rôle normatif dans leur répartition. Par construction, ces valeurs de D X restent comprises entre -0,5 et +0,5, mais en fait, leur distribution est plus resserrée : entre -0,322 et+0,337. Les valeurs extrêmes de D x représentent, pour les masses, un écart d'un facteur compris entre 1/1,251 et 1,263. Si la distribution des différences D X était aléatoire, elle pourraient aller de -0,5 à +0,5, avec un facteur touchant 1/1,414 et 1,414; leur moyenne arithmétique serait 0,250 alors qu'elle est 0,191. Cette analyse suggère qu'il existe vraiment une tendance à ce que les masses se groupent autour des valeurs puissances entières de 2.

Un petit changement dans la valeur du facteur d'échelle pris égal à 2 augmenterait la valeur moyenne de D X. Cela suggère que cette valeur possède une signification particulière pour les particules fondamentales. La figure 1 montre la distribution par niveaux des valeurs de X. Elles se rassemblent au voisinage des valeurs entières K = 0, 8, 11, 12 13,

Fig. 1. Invariance d'échelle facteur 2 pour 15 particules. En ordonnées, les valeurs de X pour les 15 particules fondamentales.

Le facteur d'invariance de la gamme tempérée

Dans l'ordre du clavier musical, les notes vont du fa au do# supérieur.

Jean-Sébastien Bach fit franchir à la pratique musicale une étape considérable en adoptant la gamme tempérée, dans laquelle tous les intervalles sont des demi-tons égaux entre eux et au douzième de l'octave. La transposition ou changement de tonique devenait ainsi beaucoup plus facile qu'auparavant. L'intervalle diatonique ainsi défini vaut un facteur racine douzième de 2 ou 2^1/12. Désignons par la lettre b ce facteur.

b = 2 ^1/12 = 1,059.463.

Invariance d'échelle facteur b (gamme tempérée)

Rappelons que le nom des notes se répètent à chaque octave : un facteur deux ou puissance entière de deux ne change pas le nom d'une note. On peut toujours ramener une fréquence choisie, par réduction d'octaves appropriées, à l'intérieur d'une octave déterminée. C'est ainsi que nous pouvons décrire la fréquence f de l'électron comme voisine du la normal, car, à plusieurs octaves ou à plusieurs facteurs 2 près, cette fréquence vaut 428,7 Hz. Le la normal admis de nos jours vaut 440 Hz.

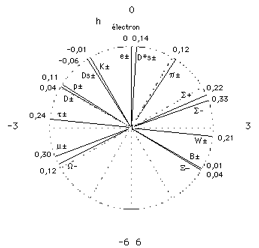
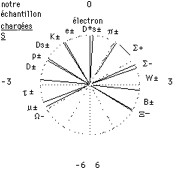
Fig. 2. Invariance d'échelle facteur b pour les particules fondamentales.

Une bonne manière de figurer cette comparaison est celle de la figure 2, où l'intervalle de l'octave occupe un cercle horaire, avec l'électron placé à midi. Le proton est au sol à 10 heures et le boson de jauge au do à 3 heures, etc. Avant d'apparaître dans cette figure, les fréquences ont été divisées par deux un nombre suffisant de fois pour les ramener dans les limites de l'octave renfermant la fréquence de l'électron prise comme la à 427,3 Hz.

Si l'accord était parfait, le rayon marquant chaque particule se placerait exactement sur l'une des positions horaires marquées par un pointillé. Chaque particule tomberait sur une heure juste et sur un demi-ton exact. On voit qu'il n'en est pas ainsi et les incertitudes sur les valeurs exactes des masses ne peuvent pas expliquer la totalité des écarts observés. Par exemple, pour le proton, l'écart est de 11 centièmes d'heure ou de demi-ton diatonique. Si l'on voulait faire apparaître cet écart en minutes, le proton serait représentépar deux aiguilles, l'une qui est figurée étant l'aiguille des heures, l'autre étant celle des minutes serait à la position de 6 minutes et 6 dixièmes après midi : en bref, le proton est à 10 heures et 6 minutes et semblablement, le boson de jauge est à 3 heures et 13 minutes, etc.

On peut mettre en évidence ces fractions de demi-ton marquant l'imperfection de l'accord entre les masses et les places exactes que l'invariance d'échelle leur assignerait. On peut tout autant s'étonner que l'accord ne soit pas plus imparfait, alors que le domaine des fréquences concernées touche 17 octaves. Cela veut dire que même pour le boson de jauge W±, la masse se fixe très près de l'un des degrés de l'échelle d'invariance, au sein d'une octave dont le la possède une fréquence valant 131.072 fois celle de l'électron.

Tout cela vaut pour les invariances d'échelle dans une gamme tempérée.

Cependant, la gamme tempérée fut précédée par des gammes de diverses descriptions donnant également 12 notes par octave, valant approximativement ceux de la gamme tempérée. Si l'on se réfère à l'histoire de la musique, on y apprend que la structure de ces gammes anciennes posait des problèmes qui excluaient certaines transpositions qui conduisaient à des discordances excessives, entre autres celles faisant passer de la tonalité en do à une tonalité en mi. Leur multiplicité rendait en outre impossible la musique symphonique parce que chaque instrument avait ses règles propres d'accord et d'exécution.

Il serait indiqué d'essayer de remplacer, dans l'octave de la figure 2, les intervalles diatoniques égaux par ceux, inégaux, de ces diverses gammes. Avant même d'avoir essayé ces remplacements, il paraît assez évident que l'une quelconque de ces gammes pourrait améliorer l'accord entre les fréquences des particules et l'échelle adoptée. Des remarques communiquées par Langlet^† au cours du XIVe congrès m'ont encouragé à réaliser les calculs requis.

Gammes et intervalles

Rappelons que les gammes anciennes distinguaient dièses d'une note et bémols de la note supérieure, alors que la gamme tempérée les confond. Ces gammes comprenaient donc, en principe, 21 valeurs par octave.

Les gammes les plus connues sont celles de Pythagore qui procède par quintes successives et celle de Zarlino, qui fait usage des rapports d'entiers simples. Tous les rapports de fréquences de la gamme de Pythagore sont obtenus par les puissances successives de 3 ramenées à une octave unique. Prenons do1 pour tonique et procédons par quintes montantes. Le do supérieur est atteint à la puissance 12e et il est 1,36 % trop haut.

Tableau III Gamme de Pythagore

Quintes

Notes	Puissance de 3	Rapports
do1	1	1
sol	3	1,5
rè	9	1,125
la	27	1,6875
mi	81	1,265625
si	243	1,8984375
fa#	729	1,423828125
do#	2187	1,06787109375
sol#	6561	1,601806640625
ré#	19683	1,20135498046875
la#	59049	1,802032470703125
fa	177147	1,3515243530273438
do2	531441	1,0136432647705078

Dans la gamme de Pythagore, les fréquences obtenues pour chacune des notes de la gamme sont toutes systématiquement plus élevées que dans la gamme diatonique. Les écarts apparaissent dans la dernière colonne du Tableau IV, dans des unités telles qu'un demi-ton diatonique vaut 0,059.463

Tableau IV Gamme de Pythagore

fréquences croissantes

Quintes, do = 0	Octave	L2fréq."Q"	D L2 = "Q" - Diaton.
do	0	0	0
do#	7	0,09474	0,0114
ré	2	0,16993	0,00326
ré#	9	0,26466	0,01466
mi	4	0,33985	0,00652
fa	11	0,50978	0,00978
fa#
sol	1	0,58496	0,00163
sol#	8	0,6797	0,01303
la	3	0,75489	0,00489
la#	10	0,84963	0,01629
si	5	0,92481	0,00815
do	12	1,01955	0,01955

Tableau V

Déviations aux octaves dans les gammes de Pythagore

Octave de départ 1,000.00

Octave	Déviation
1	1,013.64
2	1,027.47
3	1,041.49
4	1,055.70
5	1,070.10
10	1,145.12
20	1,311.30
40	1,719.51
60	2,254.80

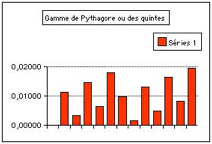
Fig. 3. On montre les écarts entre la hauteur X dans la gamme de Pythagore et la hauteur dans la gamme diatonique. La hauteur selon Pythagore est trop élevée.

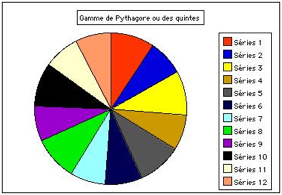
Fig. 4. Le do1 est à 0 heure midi. Un tour vaut une octave. Les hauteurs successives X apparaissent en fraction d'un tour pour la gamme de Pythagore. Les intervalles sont des demi-tons inégaux. Le do2 apparaîtrait à 0,1637 heure à droite de midi.

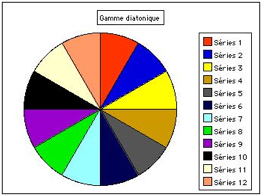
Fig. 5. Gamme diatonique. Tous les demi-tons sont égaux.

La valeur exacte de 2 est de la plus grande importance en physique classique et, nous l'avons reconnu ci-dessus, pour l'invariance facteur 2 des particules. Cela suggère de considérer avec méfiance une gamme telle que celle de Pythagore qui ne conduit pas à cette valeur exacte mais qui introduit une déviation de plus d'un pour cent à l'octave et presque un quart de ton après deux octaves. Les déviations aux octaves successives sont énumérées au Tableau V sous la forme d'un facteur.

Tableau VI

Gamme de Zarlino

	Z - d, L2	idemX12, Lb
do = 1
do# = 15/16 ré	-0,00652	-0,07821
ré = 9/8	0,00326	0,0391
ré# = 15/16 mi	-0,02118	-0,25418
mi = 5/4	-0,01141	-0,13686
fa = 4/3	-0,00163	-0,01955
fa# = 15/16 sol	-0,00815	-0,09776
sol = 3/2	0,001629	0,01955
sol# =15/16 la	-0,02281	-0,27373
la = 5/3	-0,01303	-0,15641
la# = 15/16 si	-0,01955	-0,23463
si = 15/8	-0,00978	-0,11731
do = 2	-1	0

La gamme de Zarlino est fondée sur une série des nombres entiers, ramenés à un rapport entre 1 et 2. Cette fois, le do supérieur est atteint exactement.

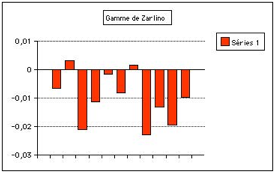
Fig. 6. Écarts entre les hauteurs dans la gamme de Zarlino et dans la gamme diatonique. Les hauteurs selon Zarlino sont trop basses sauf ré et sol

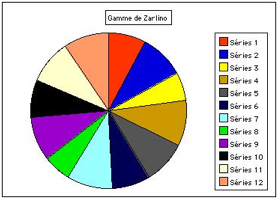
Fig. 7. Les hauteurs successives X apparaissent en fraction d'un tour pour la gamme de Zarlino. Les intervalles sont des demi-tons inégaux. Le do2 apparaît exactement à midi.

--AccueilPierreDemers.html 4eforceter.html

============================

Ann. 3. http://www.er.uqam.ca/nobel/c3410/4eforceter.html

http://www.er.uqam.ca/nobel/c3410/Tabl.periodiqueparticules.html

Tableau périodique des particules

Tableau périodique des particules

Pierre Demers

Québécium International

D'après les travaux précédents, voici un tableau des fréquences associées aux particules fondamentales. On sait qu'une fréquence f = mc²/h est associée à toute particule de masse M. Si M est en Mev :

f = M 0,409.62 2⁶⁹.

Modulo 2. Notes seules.

Les fréquences sont divisées par 2 un nombre de fois suffisant pour qu'elles tombent dans l'octave renfermant le la normal du diapason 440 Hz. Ce nombre est très grand (de 58 à 75). Les notes résultantes sont comprises entre le fa et le do# supérieur. L'électron est un la situé 58 octaves au dessus du la normal, diversement appelé la2 et la3. 9 cases sur une rangée horizontale sont occupées par 26 particules.

Tableau 1

Modulo 2. Tableau des notes des particules.

Écoutez : 440 Hz, Diapason http://www.theoriedelamusique.com/musique/diapason.html

Tabl.2isolé.html

Notes et numéros de l'octave

On distingue le numéro de l'octave pour chaque particule. Il y a maintenant 18 rangées, l'électron occupe la rangée 1 et la particule W, la rangée 18. Passer d'une rangée à la rangée supérieure représente un facteur 2 sur la fréquence.17 passages représentent un facteur 131072.. Plusieurs rangées intermédiaires sont vides, On parcourt les cases de gauche à droite et de bas en haut. La période est de 12 cases ou d'une octave et les particules situées dans la même colonne ont la même note.

Tableau 2

Tableau périodique des notes des particules.

Octave

mi

fa

fa#

sol

sol#

la

la#

si

do

do#

ré

ré#

18

W+ W-

17

16

15

14

B+ B-

13

W -

t + t -

D+ D-

Ds+ Ds-

D*^s+ D*^s-

12

P+ p-

S + S -

X -

11

K+ K-

10

9

m + m -

p + p -

8

7

6

5

4

3

2

1

e+ e-

Octave

mi

fa

fa#

sol

sol#

la

la#

si

do

do#

ré

ré#





g



g



g





g



g

Notes du clavier

L'octave 1 renferme le la60, 58e au dessus du la2 du diapason.

Liens FreqMatelt1.html NouvelleanalyseEc197.html 4eforceter.html --AccueilPierreDemers.html

============================

- 30 -