Huit nombres premiers remarquables enre 1 et 30.
Systme du
QuŽbŽcium.
Huit nombres
premiers remarquables entre 1 et 30.
Pierre
Demers, EAPD.
Traduction
interdite.
26IX2011.mˆj
17X2011
RŽsumŽ. Robert BarthŽlŽmy mÕa
fait conna”tre une propriŽtŽ des nombres premiers remarquable et inconnue
jusquÕˆ maintenant semble-tÕil RŽfs 1 et 8. Les entiers entre 0 et 30 renferment 4 paires de premiers chacune
de somme 30. JÕanalyse ses rŽsultats et il appara”t possible dÕen dŽduire le
systme mathŽmatique du quŽbŽcium avec ses applications ˆ la matire vivante et
inerte.
ExposŽ.
Robert BarthŽlŽmy me tient au courant de ses
travaux sur lÕarithmŽtique. Je prŽsente et je dŽveloppe un extrait de son
rŽcent message datŽ du dimanche 20 IX 2011 4h44 HAE heure de rŽception. RŽf.1.
Ë partir de la suite naturellement unidimensionnelle 1D des entiers de 0 ˆ 29,
cet extrait prŽsente une suite numŽrique en boucle fermŽe bidimensionnelle 2D
contenant 30 nombres allant de 0 ˆ 29. Fig. 1.
http://www.lisulf.quebec/animation
ChromoIl.gif
Fig.1. Suite numŽrique en
boucle fermŽe comprenant 30 nombres de 0 ˆ 29 dans lÕordre. DÕaprs
chromopart.jpg dans RŽf.1 et animation ChromoIl.gif dans publication.
DŽclenchez sur le lien pour faire appara”tre lÕanimation. Sont privilŽgiŽs 8
premiers en paires de somme 30.
Cet suite renferme 11 premiers,
dont 2, 3, 5 quÕon ignore, et 8 autres qui sont mis en Žvidence, qui forment
des paires en regard complŽmentaires par rapport ˆ 30, comme suit.
1+29 = 7+23= 11+19 = 13+17 = 30
Ces paires sont
des partitions binaires de 30 comprenant 2 premiers diffŽrents. LÕŽcriture met
en Žvidence au total 14 partitions binaires de 30.
Il y a 8 premiers en 4 paires. Par ses mises en
vedette en rouge, cette boucle manifeste un axe de symŽtrie horizontal. Je lui
donne plut™t un axe de symŽtrie vertical. Je remplace 0 par 30, jÕajoute 0
devant les unitŽs et je lui donne une forme circulaire-elliptique. Fig. 2.
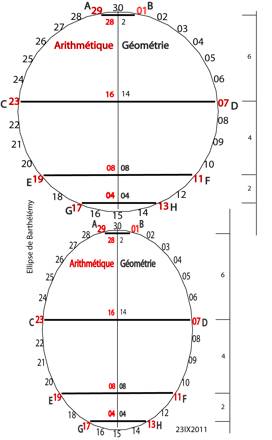
Fig. 2. Ellipse de BarthŽlŽmy. PlacŽs sur le
pourtour dÕun 30-gone de contour circulaire ou elliptique de grand axe
vertical, garni dans le sens droit, celui des aiguilles dÕune montre, les
entiers de 1 ˆ 30 ;AB, CD, EF, GH sont les 4 paires de 8 premiers se
faisant face 2 ˆ 2. Les distances ˆ lÕintŽrieur de ces paires : il y a 2
telles distances ˆ considŽrer pour chaque paire : arithmŽtique telle que
29-01=28 ou 23-07=16, ou gŽomŽtrique comptŽe en c™tŽs du 30-gone, AB=2 ou
CD=14 . ArithmŽtique et gŽomŽtrique se confondent pour les paires EF et
GH. Le sens du remplissage est arbitraire, mais une fois choisi, il faut garder
le choix. CÕest comme le choix entre matire et antimatire. On ne peut pas
revenir sur le choix qui rgne dans notre univers. - Les distances verticales
entre les paires sont 6, 4, 2. Barthé1à30bis.png
Le rŽsultat le plus frappant que devant
nous est double:
A. Voilˆ 8 premiers ABCDEFGH compris entre
1 et 30 ;
B. Voilˆ ces 8 premiers ABCDEFGH prŽsents
en face ˆ face gŽomŽtrique, formant 4 paires de mme somme 30, en dÕautres termes,
partitions binaires de 30, ce qui est rŽsumŽ dans une ligne prŽcŽdente que je
rŽcris.
1+29
= 7+23= 11+19 = 13+17 = 30
Les premiers Žtant tous impairs, on
constate bien que les 11 diffŽrences quÕils forment sont toutes paires comme il
se doit.
2, 4, 6, 8, 10, 12, 14, 16, 18, 22, 28.
On note dans cette liste lÕabsence de 20,
22 , 24 et 26. Les diffŽrences possibles, prŽsentes et absentes, sont au nombre
de 15
Fig. 2 met en Žvidence les 8 premiers
privilŽgiŽs, aux 8 points ABCDEFGH. Un de ces 8 points peut tre reliŽ ˆ 7
autres soit 56 vecteurs ou 28 valeurs absolues ou modules, si on se borne aux
distances gŽomŽtriques. DÕentre eux, 4 modules sont dŽcrits ˆ la figure 2, il
en reste 24 ˆ figurer. Fig. 3 prŽsente quelques uns, soit la collection des
vecteurs ayant A pour origine.
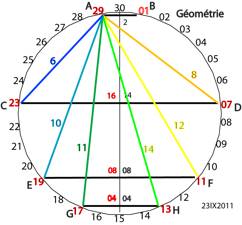
Fig. 3. Il y a 7 vecteurs ayant A pour
origine. Leur longueur est donnŽe en gŽomŽtrie.
Barthé1à30bisbis.png
Plus intŽressante est Fig. 4 qui suit,
utilisant chaque point une fois.
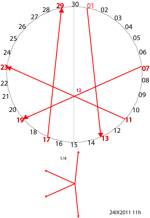
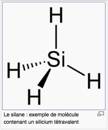
Fig. 4. Voici 4 vecteurs de longueur 12
dŽcoulant de lÕutilisation une fois de chacun des 8 premiers privilŽgiŽs, aprs
translation sans rotation et assemblage avec une origine commune. LÕaspect
rŽsultant est celui de la reprŽsentation plane dÕune liaison de tŽtravalence
chimique comme celle du silicium dans le silane, ou des sommets dÕun tŽtradre.
Barthé1à30ter24IX2011.png,
http://fr.wikipedia.org/wiki/T%C3%A9travalence
DÕaprs Fig. 4, nous dirons que lÕellipse
de BarthŽlŽmy 2Dappara”t comme une source du tŽtradre rŽgulier 3D.
EncouragŽs par cette constatation,
essayons de remplacer lÕellipse par une forme tŽtradrique, comme il sÕen
prŽsente dans le systme du quŽbŽcium, formŽe par lÕassemblage compact de 30
octadres tronquŽs. Voyez Fig. 5.
Fig. 5. Forme tŽtraŽdrique formŽe de 30
octadres. Ceci est Fig. 15 de http://www.er.uqam.ca/nobel/c3410/Unoctaedrebis.htm,
http://www.lisulf.quebec/OctaFig15.gif
Cet empilement tŽtraŽdrique dÕoctadres
rŽalise des nombres octaŽdriques, prŽsents ˆ partir du haut avec les
valeurs successives 1, 4, 9, 16 dans les strates, et avec les valeurs
cumulatives 1, 5, 14, 30. Les valeurs cumulatives suivantes seraient 55, 91...
Les nombres octaŽdriques sont apparentŽs aux nombres tŽtraŽdriques. Dans ces 30
octadres, nous avons place pour loger les 30 entiers de 1 ˆ 30. Plus
prŽcisŽment, ayons le souci de loger les 8 premiers ABCDEFGH. PuisquÕils se
prŽsentent en 2 groupements de 4, soit ACEG et BDFH il serait naturel, sous
rŽserve dÕinventaire, de leur affecter des logements eux-mmes ˆ 4 places
formant des barres, comme on en aperoit ˆ chacune des 6 artes. Je choisis la
barre de 4 octadres composant lÕarte en rouge pour ACEG et semblablement
celle opposŽe en bleu pour BDFH. Ces 2 barres sont orientŽes ˆ angle droit
lÕune avec lÕautre sans se rencontrer. Les diffŽrences arithmŽtiques entre les
divers nombres ne sont pas affectŽes par leurs placements. Fig. 6.
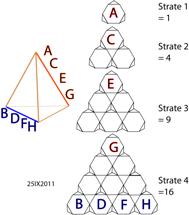
Fig. 6. Vue schŽmatique dÔun placement
partiel possible des nombres de 1 ˆ 30 dans un empilement octaŽdrique. Vue par
en dessous. Hexa123425IX2011.png
Ces 2 barres, aussi bien que 2 segments de
droites orientŽes ˆ angle droit lÕune avec lÕautre sans se rencontrer
dŽlimitent un tŽtradre.
Systme
du QuŽbŽcium.
Il reste ˆ comprendre comment placer les
22 autres des 30 nombres dans les octadres disponibles. Alors, le systme du
quŽbŽcium aura fourni un support rationnel pour manifester au moins un peu de
la thŽorie de lÕarithmŽtique des premiers et tout simplement des entiers. Ou
encore, on peut proposer que le systme du quŽbŽcium, avec ses applications ˆ
la thŽorie de la matire inerte et vivante, est autre quÕune crŽation
arbitraire, que plut™t il dŽcoulerait de la nature mme de la numŽration, plus
prŽcisŽment, de la thŽorie des nombres premiers. Ë suivre.
Remerciements.
Je remercie Guy-Robert BarthŽlŽmy pour sa
correspondance et Patrick Demers expert informaticien, pour son aide.
RŽfŽrences
RŽf. 1. Courriel GB ˆ PD.
De : Robert BARTHELEMY <lar.by@wanadoo.fr>
Date : 20 septembre 2011 04:44:33 HAE
Ë : DemersPierre <c3410@er.uqam.ca>
Objet : RŽp : IdŽe...
RŽpondre ˆ : Robert BARTHELEMY <lar.by@wanadoo.fr>
Cher Professeur Pierre Demers ,
Encore une suite d' idŽes sur les " nombres significatifs "
de la physique.. En pice-jointe et avec mes respectueuses salutations
Manosque France , o le cirque anti- dŽmocratique bat son plein .
Salutation francophone .
Dimanche 20 septembre 2011 Guy Ci- dessous , page web,
etmodifiŽe jŽgrement .
Arithmetique des chromosomes N ( C 30 )
Les chromosomes d' une cellule ,
observŽs d' un point de vue arithmetique .
par Guy Barthelemy . mise ˆ jour le 20 septembre 2011
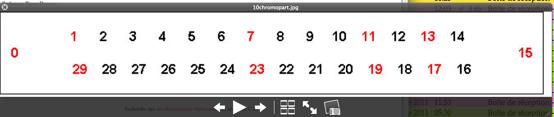
Recherche des dix chromosomes Particuliers N
( sŽquence C 30 ) ,
( image chromopart.jpg )
PropriŽtŽs particulires des dix
chromosomes arithmetiques . Tableau ^
Sur les dix ŽlŽments particuliers retenus , 2 sur 30 sont essentiels ˆ la divusion et
ˆ la ruptre de cette cellule arithmŽtique . C 0 et C 15 . Titre I et II . Ils doivent rŽpodre aux
conditions - a et - b
Les
huit autres ŽlŽments nommŽs 8
C , sont des nombres impairs et participent ˆ la divusion et ˆ la ruptre de
cette cellule arithmŽtique . Titre III . Ils doivent rŽpodre aux conditions - a et - b
Deux conditions
a Les
termes de leurs progressions doivent
appartenir ˆ la premire circularisation du systme elliptique des ŽlŽments donnŽs. ( SPIN ) .
b -
Leurs termes sont pointŽs sur les rayons , ( r 0 et r 15 ) d' un graphe tridŽcimal de 30 rayons non
pas , en progression
elliptiques , mais en ligne droite opposŽe , sur le diamtre ( r 0 et r 15 ) .
graphe v .
I - l' ŽlŽment ( C 0 + mod 30 )
Cet ŽlŽment C 0 , muni du vecteur + ,
rŽpond aux conditions a et b :
< - - ( r 0
) ____30 __________ 0 ( centre graph )
II - l'ŽlŽment ( C 15 + mod 15 )
Cet ŽlŽment C 15 , muni du vecteur + ,
rŽpond Žgalement aux conditions a et b :
graphe v .
<- - ( r 0 ) ________ 60 ___________30_________ 0 __ 15 ___ ___45 , __ ( r 15 ) . . .>
III - Chromosomes particuliers . Elements
8 C
Ce sont tous des nombres impairs et
appartiennent ˆ la sŽquence , 8 C , soit les ŽlŽments 8 C :
1 , 7 , 11 , 13 , 17
, 19 , 23 , 29 .
c - Voyons ces huit autres ŽlŽments du tableau , des chromosomes
" particuliers " , ( C 30 ) .:Ils ont tous la caractŽristique de progression en trente
termes , nŽcessaires ˆ l apremire
circularisation
complte de leur ellipse . ( SPIN
) . De mme ils rŽpondent aux conditions donnŽes en - a - et et en b -
Au total , il y a 10 sur 30 ŽlŽments , qui soient ici ,
remarquables .
( chromosomes arithmŽtiques) .
IV - Reste les vingt "
chromosomes N dŽduits " , suivants :
( image chromoded.jpg
)
Nous obtenons Vingt ŽlŽments
N diffŽrents , dans cette cellule arithmŽtique .
Remarques pour conclusion .
Le cas des deux ŽlŽments C 0 et C 15 est troublant , car ils sont mixtes et confondus , par leur complŽmentaritŽ ˆ 30 .
Les vingt ŽlŽments diffŽrents ci- dessus , sont hors de ce cadre ,
paraissent en quantitŽ , correspondre aux vingt acides aminŽs d' une cellule biologique .
Les paires de " chromosomes ŽtudiŽes " , sont formŽes des
deux termes de la composition de des nombres donnŽs .
RŽf. 2. Courriel PD ˆ GB, 21 septembre 2011
13:45:06 HAE
(NDLR :
*Vrai si on admet 1 comme 1er.)
Un tableau 2D circulaire
de 30 nombres se faisant face, 0 Žtant comptŽ comme le 1er, 29 le
dernier.
*Il renferme 8 1ers se
faisant face et donc de somme 30.
La figure a un axe de
symŽtrie un seul horizontal non vertical.
(A Entre ces 8 1ers,
on peut trouver 3 diffŽrences 16 et 1 diffŽrence 12.)
B Entre ces 8
1ers, on peut trouver 4 diffŽrences 12.
4 vecteurs de mme module
orientŽs pouvant s'agencer symŽtriquement 3D ˆ partir d'une origine commune
selon l'angle tŽtraŽdrique 109,471o.
ThŽorie des
symŽtries.
Le nombre 30 est source
du tŽtradre rŽgulier.
Le nombre 30 dans 2D est
source d'une symŽtrie 3D.
BARTHƒLƒMY21IX2011.png
Amical.
Continuez!
Pierre Demers, il est 13h45 le 21
IX 2011.
RŽf. 3.
Nombre premier. http://fr.wikipedia.org/wiki/Nombre_premier
Entre 0 et 100 :
2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 et 97.
1 et 0 sont exclus. (NDLR. Voyez cependant RŽfs 1,
4, 5).
RŽf. 4. Franois Le Lionnais 1969, EncyclopŽdie ThŽmatique
Weber,VI, 146. Ç Les modernes admettent en outre que 1 nÕest pas
premier. Il sÕagit lˆ dÕune convention sans consŽquences profondes mais qui
permet de simplifier les ŽnoncŽs de plusieurs thŽormes.È
RŽf. 5. R. Frank et J. Halbanne, Table des
nombres premiers de 1 ˆ 1000, EncyclopŽdie Larousse MŽthodique, septembre 1955,
Tome 2, p. 17
RŽf. 6. Pierre Demers 2010, Systme du QuŽbŽcium,
Les tableaux pŽriodiques 3D depuis 1862 et de nos jours. Pierre Demers EAPD.
Traduction interdite.
http://www.lisulf.quebec/3DLesTableauxTexte.htm
RŽf. 7. GŽrard
Villemin 2011, Trente,
17/10/11 http://villemin.gerard.free.fr/Wwwgvmm/AlphabT.htm#T,
Ne mentionne pas
la propriŽtŽ des nombres premiers communiquŽe par Robert BarthŽlŽmy.
- 30 -