ImpairVerlaine
PrŽfre l'impair, Art Po‘tique,
1874.
Importance de l'impair
pour comprendre la
matire et la vie.
Dans le systme du
QuŽbŽcium.
Pierre Demers
Traduction interdite.
25X2015
Verlaine en 1874.
ArithmŽticien, Verlaine disait, en 1874, dans L'Art poŽtique:
PrŽfre l'impair.
Le Systme du QuŽbŽcium en
2015. Les impairs qui le composent.
L'impair est prŽsent dans le Systme du QuŽbŽcium, en 2015, j'essaie de
mettre en Žvidence cette vŽritŽ dans une tentative de comprendre un peu mieux
ce que sont la matire inerte formŽe d'atomes, et la matire vivante, cette
dernire Žtant envisagŽe dans l'tre humain. Voici.
Noter que tout entier, pair ou impair, peut s'Žcrire comme une somme
d'impairs.
En revanche, un impair ne peut pas s'Žcrire comme une somme de pairs. Une
somme de pairs ne peut donner que des pairs.
.
.
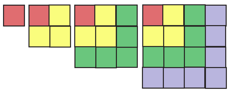
Fig. 1. 1, 3, 5, 7,
RJVB, les 4 impairs, les 4 couleurs, les 4 Žquerres. les4impairs015-10-23
à 19.39.44
. 
.
Figs 2, 3, 4, 5. Blocs.
Les 4 sortes de blocs. Bloc R = 1; bloc J = 4; bloc V = 9; bloc B = 16.
Les4,2015-10-25 à 01.06.03.png
4 impairs, 4 couleurs. En effet, me suffisent les 4 premiers impairs 1, 3,
5, 7. Ë chacun, j'attribue un graphisme et une couleur dans un canevas de 21X21
cases petits carrŽs Žgaux. Le graphisme est une Žquerre ayant 2 bras Žgaux, les
bras Žtant nuls pour 1.
7 est une Žquerre B ayant 7 petites cases, elle vient enserrant une Žquerre
V.
5 est une Žquerre V ayant 5 cases, elle vient enserrant une Žquerre J.
3 est une Žquerre J ayant 3 cases, elle vient enserrant une case unique R.
1 est une case unique, Žquerre sans bras R.
7 ne vient pas sans 5, 3 et 1.
5 ne vient pas sans 3 et 1.
3 ne vient pas sans 1.
1 peut venir seul.
Chacun des enserrements produit un carrŽ bigarrŽ dans le canevas.
"La somme des
impairs...".
"La somme des impairs est la suite des carrŽs d'entiers."
C'est-ˆ-dire, des puissances 2 des entiers. VŽritŽ inoubliable lorsqu'on
l'a comprise.
Squelette humain. 30 os dans
chaque membre. 30 est nombre magique.
Il s'agit de 30 os constants; il se prŽsente en outre, en nombre variable
selon les individus, des os surnumŽraires.
Ds 1696, le mŽdecin du roi Louis XIV le savait et l'Žcrivait. Figs 6, 7.
.6.
7.
Figs 6, 7 M. Le Clerc,
mŽdecin habituel du roi Louis XIV, 1696. 31-1 = 30 os dans le membre supŽrieur.
Pour moi, l'omoplate ou l'Žpaule est exclue du dŽcompte du membre supŽrieur. 30
os dans le membre infŽrieur. RŽf. 2.
Les membres supŽrieurs, le
gauche.
Trs apparents, je compterais 1 pouce et 4 doigts dans ma main gauche, or 4
= 1+3 , soit 2 impairs.
Mais je compterai plut™t les os isolŽs, phalanges et autres.
Je commence par l'humŽrus gauche et je lui attribue le numŽro 30 ou 30c, c
suffixe pour os. En comptant bien, je trouve 29 autres os jusqu'ˆ la phalange
distale du pouce que je numŽrote 1.
Je loge la case 30 humŽrus gauche dans l'encoignure NO du canevas. Les
numŽros des os sont portŽs dans le sens horaire. La case 30 est accompagnŽe de
15 autres cases, total 16 = 1 + 3 + 5 + 7 = RJVB. Selon une diagonale NO, se
succdent RJVB, RJV, RJ, R, dans des carrŽs de 16, 9, 4 et 1 cases. Leur total
est 30.
Systme de numŽration de base
30.
Ce systme nous est utile. On n'Žcrit pas de chiffre pour la base 10 dans le
systme de numŽration de base 10. Comme dans tout systme de numŽration on
Žcrit 1 suivi de 0, de mme, dans le systme de base 30, j'Žcrirai (1)0 pour 30, (1)1 pour 31, (2)0 pour
60, ... (4)0 pour 120.
Voici le membre supŽrieur gauche, les numŽros 30 ˆ 1 ou (1)0 ˆ 1. Figs 8,
9.
Horaire
G HumŽrus
8
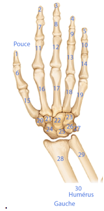..9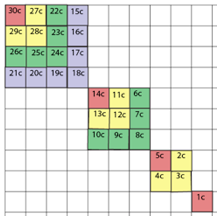
G Pouce
Figs 8, 9. Membre supŽrieur gauche. 1 pouce, (1)0 = 30
humŽrus. De 1 ˆ (1)0- Enfilade NO. Il y a 30 os. Squesupg 2015-10-08 à
10.23.19.png
30 est nombre magique.
Magique, adjectif tirŽ
du vocabulaire de la physique de l'atome.
Magie de sa prŽsence
dans le membre supŽrieur gauche de chacun des milliards d'tres humains. Dans tous
ceux qui nous ont prŽcŽdŽs.
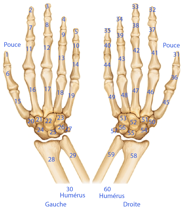
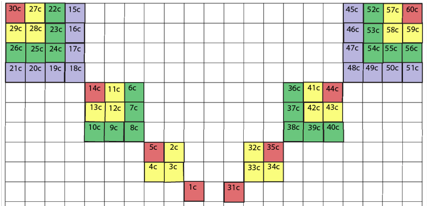
Les 2 membres supŽrieurs.
Le supŽrieur droit est numŽriquement identique au supŽrieur gauche, ˆ une
trentaine prs, de 31 = (1)1 ˆ 60 =
(2)0.
Il en est le symŽtrique miroir, le miroir Žtant un plan contenant la verticale
et passant par le nez et le coccyx. Figs 10, 11..
10.
.
Horaire
G HumŽrus D
Anti-horaire
. 
.11
G Pouce D
Figs 10, 11. Les 2
membres supŽrieurs, vue des os. - Les enfilades NO et NE. 19-49
De 1 ˆ (1)0 = 30, de (1)1 = 31 ˆ (2)0 = 60.
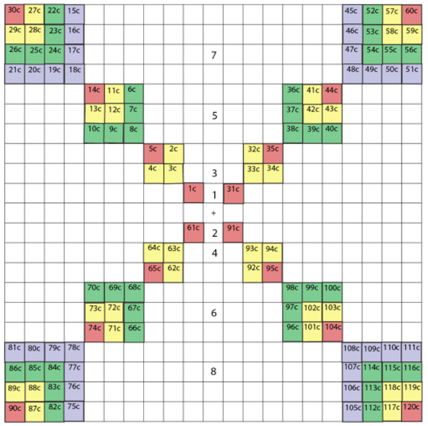
Les 2 membres infŽrieurs.
Voyez Fig. 12. Les numŽros se succdent rŽgulirement de 1 ˆ 120 = (4)0.
Horaire
G HumŽrus D
Anti-horaire
.
.
Anti-horaire G FŽmur D
Horaire
Fig. 12. PrŽsents dans
les quadrants infŽrieurs, les membres infŽrieurs sont l'image numŽrique miroir
des membres supŽrieurs, le miroir virtuel Žtant horizontal et passant non loin
du nombril. Les 2 membres infŽrieurs, les enfilades SO et SE. Ë gauche, de (2)1
= 61 ˆ (3)0 = 90, ˆ droite, de (3)1 = 91 ˆ
(4)0 = 120. - Les chiffres dans la colonne centrale: cf Fig. 9.
les4m2015-10-09 à 01.39.54.png
Et maintenant, voici les
impairs en chimie.
Le tableau pŽriodique des ŽlŽments chimiques se prŽsente, dans les
dernires versions du systme du quŽbŽcium, sous un aspect remarquablement
semblable au tableau des 120 os. Il y a 120 ŽlŽments. Ë chacun appartient une
Žtiquette unique d'un nom, d'un numŽro atomique z et des 4 nombres
quantiques RŽf. 3. Je dŽsigne un ŽlŽment par son numŽro atomique z.
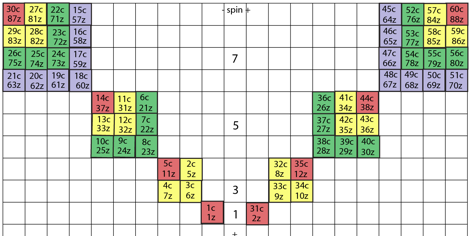
Chacun peut se placer rationnellement dans la mme case que l'un des os.
Voici le rŽsultat dans le quadrant NO pour les ŽlŽments ˆ partir de l'hydrogne
1z, lequel se place dans la mme case que l'os 1c du pouce gauche. Remarquer
les suffixes, z pour numŽro atomique et c pour os. Fig. 13.
-
Fig. 13. Comme Fig. 9, augmentŽe de 30 ŽlŽments chimiques, le suffixe z
pour numŽro atomique. Ces ŽlŽments ont le spin -. ce spin correspond au c™tŽ
gauche sur les os.
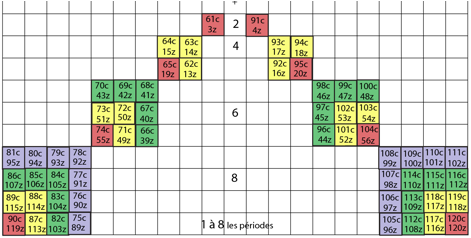
Pour obtenir le tableau des 120 ŽlŽments, il faut et suffit d'ajouter dans
chacune des 120 cases utilisŽes, le symbole de l'un des 120 ŽlŽments, bien
choisi. C'est une correspondance uni-univoque exacte, ˆ chaque os correspond
l'ŽlŽment prŽsent dans la mme case. Ainsi HumŽrus G 1c est associŽ ˆ H 1z pour
Hydrogne, FŽmur D 120c, ˆ Ja 120 c. Fig. 14.
Il reste ˆ comprendre pourquoi et comment il se fait, entre G 2c et D 119,
1o, que les os s'alignent par
numŽros consŽcutifs, alors que 2o, ce n'est pas le cas pour les ŽlŽments. 31c
est associŽ ˆ He 2z pour HŽlium, etc.
.
.
.
.
Fig. 14. Tableau conjoint des 120 os des membres humains et des 120
ŽlŽments. Chaque case contient un os et un ŽlŽment. Une couronne carrŽe renferme
une paire de pŽriodes d'ŽlŽments: une impaire et une paire. cetz2015-10-09
à 03.19.27, 023
Explications. Des
contraintes.
1o Les os. En remplissant Fig.
8, j'impose une 1re contrainte, savoir qu'ˆ chacun des membres appartient l'un des
quadrants haut-bas, gauche-droite, selon les 4 points cardinaux NSOE, dans le
canevas donnŽ et en correspondance avec les positions des membres. Demiant O
correspond ˆ membre gauche, demiant E, ˆ membre droit,
Une 2e contrainte est d'utiliser chacun des blocs tels que Figs 2, 3, 4, 5
chacun une fois seulement dans un quadrant donnŽ, selon une diagonale ajustŽe
sur une encoignure, occupŽe par un bloc B.
Une 3e contrainte est que l'os le plus massif du membre apparaisse dans le
bloc B.
Une 4e contrainte est que chaque os dŽnombrŽ a son identitŽ propre avec sa
localisation. Chaque os ne peut exister qu'en prŽsence de tous les autres tels
qu'ils sont donnŽs. On n'imagine pas un membre infŽrieur composŽ de 30 fŽmurs
consŽcutifs! Jusqu'ˆ 6 ans, un enfant qui perd une phalange terminale la
recouvre: c'est la rŽgŽnŽration RŽf. 4.
2o Les ŽlŽments. En remplissant Fig. 9, j'impose 3 contraintes, qui sont de
respecter les conditions
1 de blocs,
2 de spins indiquŽes et
3 de paritŽ des pŽriodes.
Les ŽlŽments des pŽriodes impaires 1, 3, 5, 7 sont plus lŽgers que ceux des
pŽriodes paires 2, 4, 6, 8 et sont associŽs aux membres supŽrieurs.
LatŽralitŽ biologique et
spin.
Gauche et droite, cela rŽclame avant et arrire, bouche et anus.
Fig. 14 dŽmontre une corespondance entre spin et latŽralitŽ RŽfs 5, 6.
On pourrait aussi chercher une relation avec la flche du temps.
spdf.
Combien de cases? s 16 R, p 36 J, d 40 V, f 28 B, somme 120.
RŽfŽrences.
RŽf. 1. http://explique.free.fr/jadisetn/artpoete.html
Paul Verlaine : L'Art poŽtique (composŽ en 1874)
RŽf. 2. Sur l'Žquilibre bipŽdique.
http://www.acfas.ca/publications/decouvrir/2015/10/marche-est-question-equilibre-apres-avc?utm_source=Bulletins+Savoirs&utm_campaign=aef8900f08-BS_C_2015_10_15&utm_medium=email&utm_term=0_70c699041f-aef8900f08-100216105
RŽf. 3. D'aprs Livre http://lisulf.quebec/LivreClassification2004-2015.pdf
p. 6. De l'atome. Son Žtiquette.
EnvisagŽ libre, hors de molŽcule ou de cristal, non excitŽ.
Le nom;
le symbole;
z numŽro atomique, qui peut valoir 1, 2... 119, 120; = le nombre de protons
= le nombre d'Žlectrons;
s spin s qui peut valoir - ou +;
n quantum principal, qui peut valoir 1, 2, 3, 4, 5, 6, 7 ou 8;
l quantum azimutal, qui peut valoir 1, 2, 3 ou 4; s, p, d ou f; R, J, V, B;
m quantum magnŽtique, qui peut valoir -4, -3, -2, -1, 0, 1, 2, 3, 4.;
le nombre de neutrons.
RŽf. 4. Yvan WengerDoctorantSection de
biologieUniversitŽ de Genve 24X2015
yvan.wenger@unige.ch,
Bonjour, j'ai entendu dire que certains nourrissons qui ...
www.rts.ch/.../5331744-bonjour-j-ai-entendu-dire-que-certains-nourrisso...
29 oct. 2013 - Yvan Wenger [DR] ... UniversitŽ de
Genve
... Le dŽclin de la capacitŽ ˆ rŽgŽnŽrer au cours du temps n'est pas spŽcifique
ˆ la rŽgŽnŽration du ...
Ceci nÕest possible que lorsque
lÕamputation du doigt ne dŽpasse pas la dernire phalange et que lÕ‰ge de
lÕenfant est infŽrieur ˆ 10-11 ans.
RŽf. 5. LatŽralitŽ.
http://www.chups.jussieu.fr/polysPSM/psychomot/semioRENAULT/POLY.Chp.4.html
4.1 LatŽralitŽ et latŽralisationLA
LATERALITEAsymŽtrie fonctionnelleFondements neurologiques : rŽpartition
asymŽtrique des fonctions des hŽmisphres cŽrŽbraux.
RŽf. 6. http://www.matierevolution.fr/spip.php?article923
21- QuÕest-ce que le
spin dÕune particule ou dÕun atome ?vendredi 6 fŽvrier 2009, par Robert Paris
RŽf. 7. Photo Verlaine par Otto
Wegener 49 ans 1893. Verlaine2015-10-24 à 21.44.17.png
.
.
Fig. 15.
Prince de l'Impair.
- 30 -