Magique30finaliteevolutioneehomo, http://www.lisulf.quebec/Magique30finaliteevolutioneehomo.htm

Système du Québécium.

Nombre magique 30 et

finalité de l’évolution biologique jusqu’au genre Homo.

Pierre Demers 2012.

Traduction interdite. 3XII2012. 16XII2012

Résumé. L’évolution biologique des espèces a fait apparaître aux époques géologiques récentes l’être humain avec son organisation de 30 os dans le squelette de chacun de ses 4 membres, nombre total 120. Cette organisation biologique ressemble avec une grande exactitude, à l’organisation purement mathématique et donc valable en tout temps, du nombre magique 30 qui requiert une symétrie 4, ce que l’auteur a signalé dans des publications précédentes. Une évidence aussi précise suggère que l’évolution biologique s’est réalisée selon une finalité préalable présente de tout temps et nullement définie par le hasard. (La même finalité apparaît dans la classification des éléments chimiques, puisqu’ils possèdent, depuis que la matière ordinaire existe, une organisation basée sur le nombre 30 et la symétrie 4, visible dans un tableau elliptique. Elle se présente encore dans le code génétique). Ces observations font apparaître un problème nouveau: pourquoi ce modèle mathématique s’est-il réalisé dans les faits, plutôt qu'un autre? D’ailleurs, un autre problème subsiste à peu près entier : comment ce modèle s’est-il réalisé?

Nombre 30 et symétrie 4, une récapitulation.

Voyez Réfs 1 à 7, dont voici une brève récapitulation. Le nombre magique 30 est associé au nombre 4 et à la symétrie 4 : en arithmétique pure, en théorie des premiers et en figuration géométrique 2D et 3D des nombres.

Multiplicativement, il est le produit des 4 1^ers premiers (en comptant 1 comme premier).

30 = 1*2*3*5

Additivement, il est la somme des 4 1ers carrés (en comptant le carré de 1).

30 = 1²+2²+3²+4² = 1+4+9+16

En théorie des premiers, 30 fait apparaître une symétrie quadruple : 4 paires de premiers alignées en colonnes ayant chacune 30 pour somme, entre 0 et 30

1 7 11 13

29 23 19 17

En géométrie plane 2D, plusieurs figurations se présentent, une suite de cercles ou de carrés, une grille de 120 cases... Fig. 1.

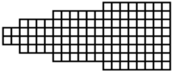
Fig. 1. Géométrie plane 2D, 120 cases. Nombre figuré 4+16+36+64=120=4*30.

En 3D, le choix est encore plus vaste, un exemple met en œuvre le tétraèdre tronqué d’Archimède. Voici une pyramide à base carrée de 30 billes. Fig. 2.

Fig. 2. Géométrie dans l’espace 3D. Nombre figuré 30 tétraèdre de billes à 4 niveaux :

1 carré de 1;

4 carré de 2;

9 carré de 3;

16 carré de 4.

Somme 30.

Bien connu, partiellement remarqué.

Les dessins d’enfants vers l’âge de 8 ans manifestent qu’ils ont compris qu’ils ont 20 doigts et orteils. Cinq doigts à chaque main et c’est l’apprentissage de l’arithmétique avec son système de numération base 10 qui commence, en leur faisant lever les 2 bras. Fig. 1.

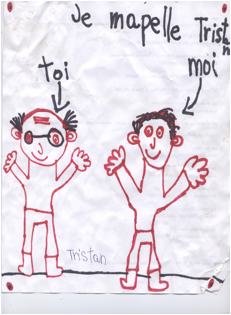
Fig. 3. Dessin d’enfant. Tristan. Vers 1970.

“Le dessin du bonhomme à 6 ans. A 6 ans, apparaissent le cou et le nombre exact des doigts. Ce sont des signes qui interviennent de façon immuable, dans tous les coins du monde, de façon universelle et éternelle ! Quand un enfant dessine le nombre exact des doigts, c’est qu’il est capable d’apprendre à lire. Dessiner un bonhomme, c’est entrer en communication avec les concepts qui se forment dans la pensée de votre enfant. Il grandit, son bonhomme se complète avec lui.”

“Le dessin du bonhomme est bien plus qu’un jeu d’enfant, c’est l’image inconsciente de son corps que votre enfant vous offre. Un vrai cadeau!” Réf. 10.

Quand enseignera-t’on aux enfants que chaque membre complet, bras ou jambe, compte 30 os, total 120 ? Mëme des articles savants ne mettent pas en évidence cette réalité qui a son importance et requiert explication. Celui de Villemin est une exception. Réfs 6, 7. Fig. 4

Répartition des 206 os constants

Fig. 4. Dans les membres, 120 os constants. Réf. 6.

Fig. 5. Dénombrement des os du membre supérieur gauche.

Main gauche,

1 la phalange terminale du pouce ;

4 les phalanges terminales des autres doigts;

9 les autres phalanges des doigts;

16 les autres os du reste du membre supérieur gauche.

Somme 30.

Pittoresque, ce dénombrement peut aussi de faire en deux puissances de 5, la 1^re et la 2^e.

1+4 = 5

9+16 = 25

5+25 = 5 ¹ +5 ² = 30

en base 5 : 1.1.0

En base 5, trente s’écrit 1.1.0.

Mais cela n’est pas notre sujet.

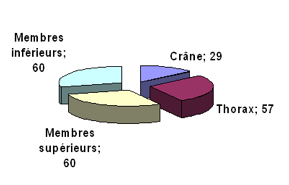
Fig. 6. Système du Québécium. Parallèle atomes et squelette, nombre magique120 et symétrie 4. Photo et graphismes Maurice Day. ACFAS en 2008 à Québec. Réf. 12.

Fig. 7. Dans un quadrant du tableau elliptique des éléments chimiques devenu tableau de poche: quadrant NE. Nombres d’éléments.

1 élément 1^re strate;

4 éléments la 2^e strate;

9 éléments la 3^e strate;

16 éléments la 4^e strate.

Somme 30.

Système du Québécium. Maurice Day et Pierre Demers 2012 Tableau de poche des 120 éléments chimiques. Traduction interdite. 30VII2012 Tableaudepoche29VII2012.htm

4 16 ….. 64 .

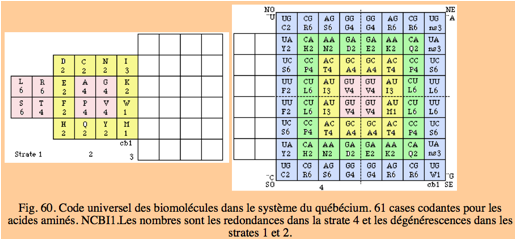
Fig. 8. Le code génétique universel dans le système du québécium; 64 cases pour les codons dans la strate 4, 20 cases d’acides aminés dans les strates 1 et 2. Pas de strate 3. 
Extrait de http://www.lisulf.quebec/QbSyst2e.6.html, QbSyst2e.6.html 10-oct -2003 23:07.

L’évolution biologique et son mécanisme.

On trouve une abondance de discussions sur l’évolution et sur l’apparition de l’homme : Lamarck, Owen et Darwin etc. Un excellent exposé de Bruno Boucher de l’Académie de Versailles http://www.svt.ac-versailles.fr/spip.php?article147

Les connaissances sur le sujet relèvent de spéculations innombrables et de l’analyse de rares fossiles. On n’a encore jamais observé l’apparition en temps réel d’une seule espèce biologique. Jacques Monod à écrit sur le sujet un livre à succès en 1987: Le hasard et la nécessité.

La présente publication offre, semble-t’il le 1^er exemple rationnel de la nécessité d’un résultat macroscopique de l’évolution : le quadri-membrisme, et le reste ; ce qui, en soi, ne touche pas le processus qui a mené à ce résultat. Cependant, elle suggère tout autant la nécessité de certains aspects du processus lui-même, savoir l’organisation de la matière physico-chimique des éléments chimiques et celle du code génétique. À suivre.

Références.

Réf. 1. Pierre Demers 2012 et auparavant. Système du Québécium. quebecium.htm

Réf. 2. Pierre Demers 2012. Système du Québécium. Le nombre 30, nombre magique commun à plusieurs domaines du savoir. 2XII2012. Nombres%20magiques%20communs.htm

Réf. 3. Pierre Demers 2012. Système du Québécium. Suites des Premiers en Base 30. Traduction interdite. 18XI2012, version du 3XII2012. PremiersBase30.htm

Réf. 4. Questions posées à Jean-Luc Gouin, le philosophe de la rationalité en tout temps et hors du temps. 3XII2012 LePeregrin@yahoo.ca,

Réf. 5. Questions posées à Aubert Daigneault, mathématicien de l’univers éternel. 3XII2012 aubert.daigneault@umontreal.ca,

Réf. 6. Gérard Villemin. http://fr.wikipedia.org/wiki/Squelette_humain#Bras_:_hum.C3.A9rus

Réf. 7. Pierre Demers 2012. Système du Québécium. Le Platonicisme QbPlaEvoAtoXI2007bis

Réf. 8. Pierre Demers 2012, DeFibonacciauQuebecium.htm

Réf. 9. Jean Choay 29XI2010, Jacques Monod, « Le hasard et la nécessité : L'homme n'est qu'un ...

laquinzaine.wordpress.com/.../jacques-monod-le-hasard-et-la-necessit...

Réf. 10. Guy Delaporte 3II2001. L'homme n'est qu'un accident,

Hasard, nécessité, finalité - Grand Portail Philosophie Thomas d'Aquin

www.thomas-d-aquin.com/Pages/Articles/Hasard.pdf

Ce numéro montre que le livre de Monod « Le Hasard et la Nécessité » sert toujours de référence fondamentale.

Extraits: « les phénomènes biologiques sont réductibles aux lois de la physico-chimie, donc régis par leur nécessité, ils ne sont cependant pas déductibles de ces lois car seul le hasard les a créés….

L’homme non seulement n’est plus le centre du monde, mais il n’est plus inséré dans un réseau de déterminations qui rendait sa présence déductible…Les systèmes post-hégéliens de Marx et de Engels ne sont pas davantage épargnés...”

NDLR. Faut-il encore accepter ces affirmations concernant seul le hasard, l’homme centre du monde, et sa présence déductible?

Réf. 11. Edwige Antier, 2009 Pédiatre, auteur de "Elever mon enfant aujourd'hui, ancienne députée, "edwigeantier@me.com, apprentissages eveil dessiner un bonhomme.

Réf. 12. Pierre Demers 2007, http://www.er.uqam.ca/nobel/c3410/ACFAS2008QbPlaEvoAtXI2007.htm

Réf. 13. Maurice Day et Pierre Demers 2012 Système du Québécium. Tableau de poche des 120 éléments chimiques. Traduction interdite. 30VII2012 Tableaudepoche29VII2012.htm

- 30 -