Nombresquelettehumainevolution, http://www.lisulf.quebec/Nombresquelettehumainevolution.htm

Système du Québécium

Le nombre, le squelette humain

et l’évolution biologique

Pierre Demers

Traduction interdite.

3I2013. 10I2013.

Sommaire. On montre que le squelette humain réalise au moins 4 suites arithmétiques de nombres. Chacune constitue un plan précis, éternel et omniprésent. A. La 1^re suite s’applique aux 4 membres, supérieurs et inférieurs; elle dépend du nombre 30 et de la symétrie 4 qui l’accompagne. BC La 2^e et la 3^e sont les progressions arithmétique et géométrique, l’une et l’autre de 1^er terme 2 et de raison 2, s’appliquant à la dentition. D La 4e est la suite de Fibonacci appliquée aux rappports des longueurs des membres. E On évoque des applications à d’autres parties du squelette telles que la colonne vertébrale, le crâne, le thorax et les grands os plats. F Cela suggère que l’évolution biologique ne s’est pas faite par pur hasard, puisque les nombres et leurs rappprts ont existé de tout temps et ont précédé l’apparition de squelettes humains. Référence Jacques Monod Le Hasard et la Nécessité Seuil. G Cela conduit à des réflexions sur ce que sont un nombre et un nombre figuré.

A Nombre magique 30: les 120 os du squelette des membres. Réfs 1 à 7.

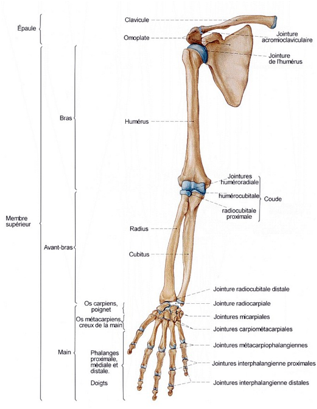
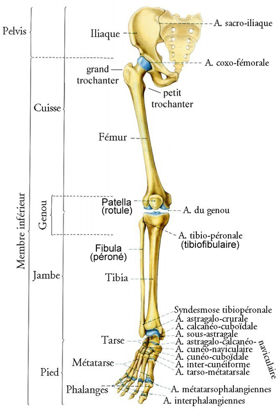
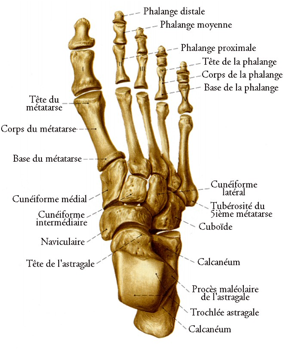
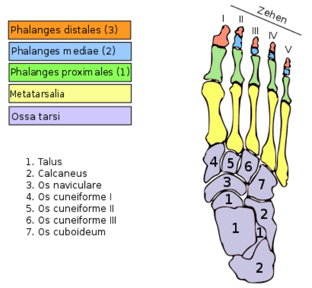
Fig. 1. Squelettes des membres. Les 30 os de chaque membre supérieur, les 30 os de chaque membre inférieur. Noter les 8 os du carpe dans la main et les 7 os du tarse dans le pied. Noter les os sésamoïdes, en supplément au squelette et présents occasionnellement comme ici, à la base du pouce. Zehen : orteil.

« On a toute raison d’appeler 30 nombre magique. Parmi tous les entiers, il se distingue. Pythagore se réjouirait, lui qui disait « Tout dans le monde est nombre ». Y compris précisément l’être humain que tous les enfants dessinent partout et toujours avec 2 membres supérieurs et 2 membres inférieurs, et tous ces enfants et toutes les grandes personnes ont chacun 30 os dans le squelette de chacun de ces 4 membres.

Ce n’est pas un hasard s’il en est ainsi. Chaque personne humaine réalise à son tour un plan éternel et omniprésent, celui qui dépend du nombre 30 et de la symétrie 4 qui l’accompagne.» Extrait de Réf. 3.

La suite d’entiers qui se manifeste est celle de 1, 4, 9, 16 répétée 4 fois.

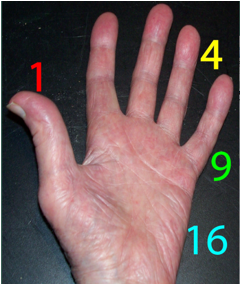
Fig. 2. Main gauche (et bras gauche). 22013.png.

Dénombrements.

1 phalange terminaledu pouce.

4 phalanges terminales des autres doigts.

9 autres phalanges.

16 autres os de la paume, du poignet et du bras.

------------------------------------------------

30 os total dans le membre supérieur gauche.

X 4 membres = 120 os total général.

Les membres inférieurs répètent exactement les dénombrements des membres supérieurs, avec une particularité qui ne change pas la suite 1, 4, 9, 16. La voici : alors que chaque bras compte 3 des 16 éléments et la main 13, la jambe compte 4 éléments et le pied 12.

Le présent exposé ajoute à la Réf. 4, dont voici un extrait.

« L'existence de ces 120 os et leur organisation mutuelle, est une conséquence de lois naturelles, et le système du québécium en manifeste les aspects apparaissant dans cette figure. En confondant les lois et leur manifestation, le système du québécium "impose" l'existence de ces 120 os et leur organisation ou il en est la raison d'être. »

Leur organisation peut s’exprimer dans la suite 1, 4, 9, 16 multipliée par 4.

Le décompte des groupes 1, 4 et 9 dans les mains se fait sans peine par chacun s’il s’arrête à examiner ses doigts. Celui du groupe 16 est moins immédiat et l’image aux rayons X rend alors service. Fig. 3. Même alors les 8 éléments du poignet formant le carpe sont difficiles à discerner.

Une remarque semblable vaut pour le décompte dans le pied. Le décompte des 7 éléments formant le tarse exige attention.

BC Nombre magique 30, progressions de raison 2: la dentition. Réfs 8 à 11.

Symétrie 4. Les dents occupent 4 demi-arcades sur les gencives. Elle manifestent une double symétrie binaire : haut-bas et droite-gauche, c’est-à-dite quadruple, aussi bien que les 4 membres, dans la 1^re dentition et dans la 2^e. La 1^re dentition, celle des dents de lait, commence habituellement vers 6 mois par deux incisives en bas, suivies bien vite par 2 autres en haut, il y a finalement 5 dents de lait dans chaque demi-arcade. Elles tombent vers 12 ans pour être remplacées par les dents d’adulte. dont les dernières ou dents de sagesse apparaissant parfois seulement à 26 ans. La 1^re dentition compte 4 fois 5 dents, la 2^e, 4 fois 8 dents. Réfs 11, 12.

Les types de dents sont ainsi : i pour incisive, c pour canine, p.m. pour petites molaires parmi les dents de lait, p pour prémolaire, m pour molaire.

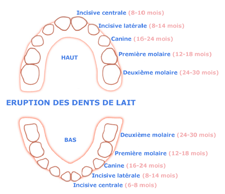
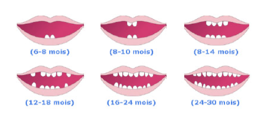
Fig. 3. La 1^re dentition et quelques étapes de son apparition. Elle réalise successivement, sauf 18, tous les termes de la progression arithmétique de base 2 et de raison 2, depuis 2 jusqu’à 20.

Fig. 4. Les dents définitives. Au nombre total de 32 vers 21 ans.

L’organisation des 1res dents suggère l’intervention des 2 1ers termes de la série 1, 4, (9, 16), total 5 comme pour les phalanges des doigts et des orteils, c’est-à-dire d’un plan lié au nombre magique 30.

L’organisation des dents définitives suggère l’intervention d’un plan différent lié à la progression géométrique ayant 2 comme 1^er terme et 2 comme raison. On y aperçoit en effet les 5 1^ers termes de cette progression, de 2 à 32.

2, 4, 8,16, 32.

Ainsi se trouve mis en évidence à nouveau le nombre entier 5, lequel apparaît dans l’organisation des 1res dents.

Ne pas confondre 32 = 2*2*2*2*2 = 2⁵ et 36 = 2*2*3*3 =2²*3².

D Suite de Fibonacci dans les mains et les pieds (longueurs) . Réf. 12.

La suite des phalanges se continue dans la paume par un 4^e os pour 4 doigts et par un 3^e os pour le pouce. Les doigts ainsi prolongés s’appellent des rayons. Fig. 2, on reconnaît la vérité approximative de cet extrait : « La longueur des composantes de chacun des rayons s'inscrit dans la série de Fibonacci découverte en 1202 voulant que chaque élément est égal à la somme des deux précédents.» (0, 1), 1, 2, 3, 5….

La série de Fibonacci fut décrite par son auteur en termes de nombres entiers puisqu’il l’appliquait à des portées de lapins. Ici elle est appliquée à des longueurs. Fig. 5.

Le pied, comparé à la main, renferme le même nombre d’éléments dans ses rayons. On remarque en outre que le 4e élément est de beaucoup supérieur à la somme du 3e et du 2^e. Réf. 4.

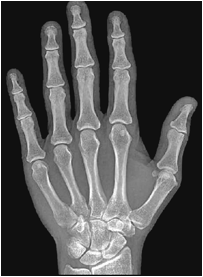
Fig. 5. Radiographie d’une main humaine. Dans les rayons des doigts, on reconnaît la suite des longueurs 5, 3, 2, 1.

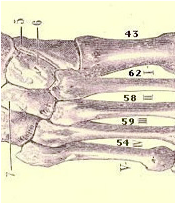
Fig. 6. Un pied humain.

Les rapports sont ainsi.

43/22/28, 62/17/11/10, 58/15/7/11, 59/15/6/10, 54/18/6/8,

1,5/0,8/1, 6,2/1,7/1,1/1, 5,3/1,4/0,6/1, 5,9/1,5/0,6/1, 6,8/2,3/0,8/1,

en arrondissant à l’entier le plus proche :

…..2/1/1, 6/2/1/1, 5/1/1/1, 6/2/1/1 , 7/2/1/1.

Fibonacci serait :

…..3/2/1, 5/3/2/1, 5/3/2/1, 5/3/2/1, 5/3/2/1.

On souhaiterait établir des statistiques par de telles mensurations pratiquées sur plusieurs individus.

E Les entiers dans le squelette du crâne, du thorax et de la colonne vertébrale. À venir.

Dans le crâne on reconnaît 4 paires d’orifices : le nez, les yeux, les oreilles et les gencives.

Dans le squelette thoracique, on reconnaît 24 côtes.

Dans la colonne vertébrale, on reconnaît près de 33 vertèbres.

Entre la colonne vertébrale et les os des membres on reconnaît les grands os plats : les 2 omoplates et les 2 os iliaques, total 4 os.

Une analyse à venir.

FG. Jacques Monod et qu’est un nombre? Les idées de Platon. Réfs 13 à 18.

• Dans son œuvre mémorable, Jacques Monod fait la part du hasard et celle de la nécessité dans l’apparition des êtres vivants et en particulier, celle de l’être humain. La seule nécessité qu’il semble reconnaître à ce propos paraît être celle des phénomènes physico-chimiques. Voici son texte.

« les phénomènes biologiques sont réductibles aux lois de la physico-chimie, donc régis par leur nécessité, ils ne sont cependant pas déductibles de ces lois car seul le hasard les a créés… »

Veut-il dire : créé les phénomènes, ou les phénomènes et les lois aussi?

De toute façon, cet auteur semble indifférent aux lois des mathématiques. Les lois de la physico-chimie sont assurément liées à la matière et on peut prétendre qu’elles n’existent pas en dehors de la matière. Mais peut-on avancer la même prétention pour les lois des mathématiques ?

Les lois des mathématiques commencent avec la notion de nombre, et celle-ci, avec la discernabililité de régions de l’espace-temps pemettant de compter un, deux… Les mathématiques, fondamentalement, jouent avec des nombres, qui sont des abstractions et qui n’ont en elle-mêmes aucune consistance matériielle, mais que les humains ont trouvé nécessaire de symboliser pas des objets concrets, cailloux, chiffres, figures géométriques à 2 ou à 3 dimensions. Ou par des formes d’un langage écrit ou parlé. Ces formes ne sont pas des nombres, ils les évoquent et on les appelle « des nombres imagés ». Le squelette des membres est 120 nombre imagé.

Les nombres sont des idées, des abstraits.

Ils ont toujours existé, ils existent partout et leurs vérités sont aussi solidement établies que celles des lois de la physico-chimie.

Si Jacques Monod en rédigeant son livre prestigieux avait ajouté à son expression ci-dessus, en écrivant physico-mathématico-chimie plutôt que physico-chimie, aurait-il poursuivi son exposé de la façon que l’on sait? La question se trouve posée à ses admirateurs d’aujourd’hui.

•• « Que le Dieu d'Amour s'incarne en nos coeurs en cette sainte saison et chaque jour de l'année à venir. » Voilà le message qu’adressait, à l’auteur de le présente publication, le professeur émérite du Département de mathématiques et de statistiques de l’Université de Montréal Paul Gauthier, à la suite d’une rencontre de Noël dans le Hall d’honneur de cette université, hall baptisé au nom de Roger Gaudry.

Il m’a appporté un terme qui me manquait dans mon vocabulaire: « incarnation ». Dans son sens religieux bien approprié pour le temps festif des chrétiens, mais aussi dans son sens propre d’introduction, dans une chair, de quelque chose d’immatériel et pour moi cette chose est l’idée toute naturelle et mathématique du nombre 30 que je développe ci-dessus.

Dans mon enfance, j’entendais dire autour de moi : «Charlot est là, en chair et en os ! »

Devant la crèche de nos églises, les fidèles chantent : « Chantons tous son avènement. »

Le disciple aimé, saint Jean l’apôtre, écrivait à la 1^re ligne de son évangile : « Au début de tout était le Verbe», et à la dernière : « Et le Verbe s’est fait chair… »

Le Verbe, la parole, l’idée qui a toujours existé.

Est-ce là une homélie? C’est en tout cas une manière d’affimer que sans le Verbe idée du nombre, nous ne serions pas là.

Les Rois 2013.

Rrmerciements.

Je remercie Maurice Day qui m’a aidé dans la recherche des références,

Références.

A Squelette des membres.

Réf. 1. René Saint-Jacques 2012, Anatomie,

http://www.corpshumain.ca/index_fr.php et et cherchez dans Squelettique, Bras et mains; Jambes et pieds. Un bouton en forme d’œil affiche les légendes.

http://www.corpshumain.ca/images/Squelette_bras_full.jpg

http://www.corpshumain.ca/Os_jambe.php

Réf. 2. Zehen, a/s Maurice Day. http://www.futura-sciences.com/fr/definition/t/medecine-2/d/metatarse_8309/

Réf. 3. Pierre Demers 2012. Système du Québécium. Le Plan de l’Être humain est inscrit dans le Nombre 30 de toute Éternité. Traduction interdite.14XII2012. PlanHumain30Eternite

Réf. 4. Pierre Demers 2012. Système du Québécium. Voir après Fig,. 7. « L'existence de ces 120 os et leur organisation mutuelle, est une conséquence de lois naturelles, et le système du québécium en manifeste les aspects apparaissant dans cette figure. En confondant les lois et leur manifestation, le système du québécium "impose" l'existence de ces 120 os et leur organisation ou il en est la raison d'être. »

http://www.er.uqam.ca/nobel/c3410/QbPlaEvoAtoXI2007bis.htm

Réf. 5. Pierre Demers 2012. Système du Québécium. Le nombre magique 30 et la finalité de l’évolution biologique jusqu’au genre Homo. Traduction interdite. 3X2012. Magique30finaliteevolutioneehomo.htm

Réf. 6. Pierre Demers 2012. Système du Québécium. Embryologie et théorie des nombres. Dominance de 1, 2, 4. 31VIII2010. EmbryoNombres.htm

Réf. 7. Pierre Demers 2012. Système du Québécium. Modèle du Québécium et anatomie comparée des vertébrés. Suite de Fibonacci chez quelques vertébrés pentadactyles : Humain, Gorille, Orang-Outang, Chimpanzé, Bonobo, Loris grêle. 24VI2009 00FiboPentaquinte%20.htm

BC Dentition.

Réf. 8. Ordre des dentistes du Québec.

http://www.odq.qc.ca/Protectiondupublic/Soinspréventifs/Dentition/tabid/216/language/fr-CA/Default.aspx

http://www.ohdq.com/Sante/Conseils/Eruption.aspx

Réf. 9. http://www.doctissimo.fr/html/sante/dentaire/sa_dents2.htm

Réf. 10 http://www.doctissimo.fr/html/grossesse/bebe/bobos/articles/dents-de-lait.htm

Réf. 11. http://www.9mois-emoi.com/bebe-est-la/les-examens-de-bebe/les-dents-de-lait.html

D Fibonacci.

Réf. 12. http://manus.crchul.ulaval.ca/anatomie/html/squelette.html

« La longueur des composantes de chacun des rayons s'inscrit dans la série de Fibonacci découverte en 1202 voulant que chaque élément est égal à la somme des deux précédents. »

FG Évolution Nombre figuré.

Réf. 13. Paul Gauthier 2012, Le 26 déc. 2012 à 10:18, gauthier a écrit :

Saluts Pierre,

Que le Dieu d'Amour s'incarne en nos coeurs en cette sainte saison et chaque jour de l'année à venir.

Réf. 14. Jean Choay 29XI2010, 

Jacques Monod, « Le hasard et la nécessité : L'homme n'est qu'un ...

http://laquinzaine.wordpress.com/2010/11/29/jacques-monod-le-hasard-et-la-necessite-lhomme-nest-quun-accident/

Réf. 15. Guy Delaporte 3II2001. L'homme n'est qu'un accident,

Hasard, nécessité, finalité - Grand Portail Philosophie Thomas d'Aquin

http://www.thomas-d-aquin.com/Pages/Articles/Hasard.pdf

Ce numéro montre que le livre de Monod « Le Hasard et la Nécessité » sert toujours de référence fondamentale.

Extraits: « les phénomènes biologiques sont réductibles aux lois de la physico-chimie, donc régis par leur nécessité, ils ne sont cependant pas déductibles de ces lois car seul le hasard les a créés… »

L’homme non seulement n’est plus le centre du monde, mais il n’est plus inséré dans un réseau de déterminations qui rendait sa présence déductible…Les systèmes post-hégéliens de Marx et de Engels ne sont pas davantage épargnés...”

NDLR. Faut-il encore accepter ces affirmations concernant seul le hasard, l’homme centre du monde, et sa présence déductible?

Réf. 16. G. Eschbach, Fils du hasard et de la nécessité  http://www.meta-noia.org/anthropologie/5/h01.HTM « l’absolue ‘objectivité’ du ‘discours’ chimique constitué par hasard et par nécessité. »

www.meta-noia.org/Auteur.htm G.Eschbach@meta-noia.org

Réf. 17. Villemin Nombres figurés. http://villemin.gerard.free.fr/aNombre/FIGURE/Figure.htm

Réf. 18. Jacques Monod, Le Hasard et la Nécessité, Seuil 1970.

Le hasard et la nécéssité - Jacques Monod - Google Books

books.google.com/books/about/Le_hasard_et_la_nécéssité.html?id...

Title, Le hasard et la nécéssité. Author, Jacques Monod. Publisher, Editions Du Seuil, 1970. Original from, the University of Michigan. Digitized, Oct 8, 2007 ...

http://books.google.ca/books?id=-sVLAAAAMAAJ&hl=fr&source=gbs_similarbooks

Traduction en anglais.

- 30 –