Nouscherbis

Système du Québécium.

Obtenir le tableau périodique des éléments à partir des 1ers principes.

Une tentative de géométrie quantique.

Pierre Demers.

Traduction interdite

18XII2010

Obtenir. 2118

Système du Québécium. Obtenir le tableau périodique des éléments chimiques à partir des 1ers principes. Une tentative de géométrie quantique.

Résumé. Je recommence, ayant tenté plusieurs fois depuis 1995 de formuler un cadre théorique qui expliquerait le tableau périodique des éléments dans son entier alors que l’atome de Bohr-Schrodinger ne s’applique tel quel qu’à l’hydrogène. Scerri a rappelé qu’aucun principe n’explique la suite connue de peuplement des périodes. Mon présent essai insiste sur 2 conditions s’ajoutant aux règles d’interdiction connues sur snlm et ne fait aucune référence à des conditions énergétiques. 1o Il existe d’avance une grille géométrique de cases codées à remplir, selon un trajet muni de conditions quantiques ; 2o les éléments sont associés en tétrades, règle justifiée par des associations saturantes des cônes de précession des spins. Ainsi se trouve imposée l’apparition de 4 strates de 2 périodes égales, s’accordant avec le peuplement connu des périodes. Ces conditions conduisent à la formation naturelle de la suite numérique 4, 16, 36 et 64, que j’appelle suite du québécium. On arriverait peut-être à les formuler en termes analytiques. Je suggère qu’elles sont des premiers principes, continuant ceux des mécaniques ondulatoire et quantique. La question des éléments irréguliers sera examinée à part. D‘après Réf. 1.

image2118.gif (Image GIF, 230x539 pixels)

Introduction. Avec l’addition du passage en bleu « s’accordant avec le peuplement connu des périodes », le résumé ci-dessus reproduisant  le texte soumis à l’ACFAS en 2010 pour 2011 s’applique à la présente publication. – Je recommence la recherche d’une récriture nouvelle, qui me conduit à l’énoncé de premiers principes quantiques et géométriques d’où découle le tableau périodique des éléments avec son peuplement connu, présenrement inexpliqué au delà de z = 20.

Nous cherchons des principes premiers. Nous les appellerons simplement principes. En tout premier lieu, nous acceptons les règles connues concernant les 4 paramètres ou nombres quantiques snlm avec leurs interdictions, on ajoute z, ces 5 nombres étant inscrits dans une case numérotée z. Un élément est défini par 5 nombres zsnlm, le paramètre z dépendant des 4 autres. Ces 4 ou ces 5 paramètres forment ce qu’on appelle le caractère d’un atome.

caractère = (zsnlm), symbole

Les 4 paramètres snlm variables indépendantes définissant un atome sont ceux de son électron de valence. On ajoute aussi le paramètre z et le symbole, soit 6 données utiles au total.

Remarquez que ces 5 paramétres ne sont pas des variables continues, telle masse ou vitesse. Ils ne peuvent prendre que des valeurs discrètes, en accord avec la théorie, ce qui est le propre d’une quantification. Cette particularité facilite leurs représentations graphiques, qui peuvent être discontinues.

Le problème d’un seul électron autour du noyau, celui de l’atome H, est fort bien connu et résolu. Le problème de plus qu’un électron autour d’un noyau est celui de leur cohabitation dans un espace restreint. Les règles d’interdiction admises jusqu’à maintenant ne suffisent pas. J’essaie d’en définir d’autres.

Principe 1. Les règles admises concernent les 4 nombres quantiques avec leurs interdictions.

Ces règles sont des principes justifient exactement le contenu de chaque case prise isolément mais pas le peuplement des périodes, càd la succession des cases réalisées. Je vais essayer de les compléter en trouvant d’autres principes.

Construction. Ce qui veut dire occuper une case après l’autre. Une espèce atomique z est définie par ce contenu d’une case z augmenté de celui des cases de 1 à z-1 non récrit par économie. z est à la fois numéro d’ordre de l’élément, nombre de protons dans le noyau et nombre d’électrons alentour de celui-ci.

Cela signifie que le peuplement doit commencer par z=1 et non par une valeur arbitraire de z. Il doit continuer par z=2, 3 etc.

Je rappelle le principe d’exclusion. À l’intérieur d’un atome, il ne peut pas exister 2 électrons ayant le même quadruplet de valeurs de snlm.

Énergie. Et le principe de moindre énergie potentielle. Dans un atome stable, chaque électron possède la moindre énergie potentielle compatible avec les contraintes qui lui sont imposées. L’hydrogène donne l’exemple dans le diagramme de Grotrian, états s. La règle s’applique à la statique des systèmes macroscopiques. Hormis ce principe universel, je crois possible d’élaborer une théorie de l’atome sans invoquer les énergies, par exemple ceux des niveaux d’énergie individuels de l’atome H excité comme je l’ai fait jusqu’à mon avant-dernière publication sur le sujer.

Principe 1bis. Le nombre 4, le spin.

Ce nombre intervient plusieurs fois. Cette nécessité me paraît associée au plus simple des solides de Platon, le tétraèdre. Quatre est le plus petit nombre de faces planes suffisant pour enfermer un espace 3D. Quatre spins s’associent de façon saturante pour dessiner un tétraèdre

Les paramètres s, l, m.

Principe 2. Les valeurs de l sont figurées par la couleur des cases.

BVJR au lieu de l=3210, symboles fdps. Cette convention économise les écritures.

Principe 2bis. Dans une grille de carrés, nous plaçons une colonne de 4 cases colorées figuratives du quantum azimutal l. Ce sont les cases initiales.

C’est ce qui apparaît dans Fig. 1. La distance entre une case et l’origine est égale au quantum azimutal l, qui est un entier inférieur à n quantum principal, entier lui aussi. Nous procédons en admettant sans discussion l’usage d’une grille carrée. Comme les carrelages dans certaines stations du métro montréalais, et bien d’autres. Il sera à notre usage. Le carré est une projection principale d’un tétraèdre régulier, cette projection donnant 8 portions de droite dont 4 définissent un carré et 4, les demi-diagonales de celui-ci.

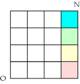
Fig. 1. Dans une grille montrée ici partiellement, une colonne aux couleurs BVJR synonymes des notations du quantum azimutal fdps ou l= 3210. Grille2.png Grille2.ai

C’est la colonne de départ. Nous posons cette exigence que l’occupation de la grille doit commencer par l’une de ces 4 cases. Il y aura 4 grilles.

Principe 3. Mise en équerre. Nous modifions la grille Fig. 1 en faisant apparaître des équerres remplissant le quadrant NO. Chaque case est un binôme lm, m quantum magnétique.

Ceci est plus qu’une convention. Dans cette mise en équerre, nous obtenons un nombre 2l+1 cases de chaque couleur. Ce nombre est lié à l’effet Zeeman. Comme l est un entier, ce nombre est nécessairement impair et forme naturellement une équerre symétrique. L’équerre s n’a pas de bras. Ces équerres sont le signe de l’occupation, et donc de la nécessité, d’un espace 2D pour décrire l’atome. Les équerres s’emboîtent selon la règle que la somme des impairs est égale à la suite des carrés des entiers. Le quantum magnétique m va de -l à l, zéro compris. Il est inscrit dans chaque case. Fig. 2.

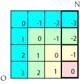
Fig. 2. Dans cette grille réduite à un quadrant, figurent les 16 valeurs possibles du binôme lm. On lit l par la couleur, m par les chiffres augmentés du signe – au besoin. Chaque binôme occupe une position uniquement définie. Grille3.ai Grille3.png

Principe 3bis. La condition de la moindre énergie fait que les cases mises en évidence sont munies d’un nombre quantique principal.

Fig. 2bis. Les valeurs de n dans les cases initiales. Grille3bis.ai Grillebis.png

Les binômes sont ainsi B4, V3, J2, R1. Fig. 2bis.

Principe 3ter. Nous posons cette exigence que l’occupation de la grille doit commencer par l’une de ces 4 cases et se poursuivre par les valeurs croissantes de m et décroissantes de l.

La colonne de départ, mise en évidence, devient celle des cases binômes. B-3, V-2, J-1, R0. La suite des valeurs de m dans chaque équerre a quelque chose en commun avec la règle empirique de Hund qui déclare que le tableau des éléments se remplit par blocs ayant même valeur de l, demi-blocs spins – d’abord, demi-blocs spins + ensuite. Mais il n’est pas question des spins dans Fig. 2.

Voilà pour les paramètres l et m. Occupons-nous d’un 3^e paramètre, le spin, en ajoutant un quadrant NE à la grille restant toutefois incomplète.

Principe 4. Dans la grille figurative encore incomplète, le spin – occupe le quadrant Ouest, le spin +, le quadrant Est. On passe d’Ouest en Est et réciproquement, par une symétrie miroir.

Ce que représente Fig. 3. Le plan du miroir passe par l’axe contenant le nord N. La mise en évidence d’une colonne est propre au quadrant NO et n’est pas répétée dans le quadrant NE.

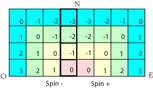
Fig. 3. La symétrie du miroir passant par l’axe N s’accorde avec la symétrie -+ des spins. Il n’y a pas de mise en évidence dans le quadrant NE. Grille 4.ai Grille4.png

Atttention : miroir. 1. Objet plan réfléchissant qu’on peut utiliser pour se mirer, tel nappe d’eau tranquille (fable de Narcisse), galerie des glaces Opéra Garnier de Paris, miroir de toilette, miroir des grâces (vanité)placés . 2. Objet idéal géométrique plan contenant v.g. les axes x et y, transformant (versant) un ensemble de points xyz une image résultante xy-z. 3. L’ensemble des points de cette image résultante. –

Miroirs dièdres, dièdre de miroirs. 1. Formé de 2 miroirs 1, 2 v. g. ayant un axe x en commun dont l’un contient l’axe z et l’autre, l’axes y.

Encore une fois, nous disons que la suite des valeurs de m dans chaque équerre a quelque chose en commun avec la règle empirique de Hund qui déclare que le tableau des éléments se remplit par blocs ayant même valeur de l, demi-bloc spins – d’abord, demi-bloc spins+ ensuite. Il est question des spins dans Fig. 3, de sorte que le rapprochement est plus complet que dans Fig. 2. Jusqu’ici, les cases ne représentent pas des éléments puisqu’il y manque l’affichage des valeurs de z et de n, mais elles sont présentes et disponibles dans les nombres voulus pour représenter, par exemple, les 6 éléments du bloc p en jaune J (3 éléments du demi-bloc spin – et les 3 autres éléments du demi-bloc spin +) d’une période.

Retrouvons la symétrie carrée. Le carré NO quadrant des Figs 1 et 2 est devenu rectangle N dans Fig. 3. Pour compléter la figuration de la grille complète et du coup retrouver la symétrie carrée, nous utilisons un miroir haut–bas, le plan du miroir passant par l’axe OE. Ce sera alors notre grille figurative complète Principe 5.

Principe 5. La grille figurative complète en un carré s’obtient en ajoutant au demiant N précédent son miroir S.

En principe la grille s’étend indéfiniment aux 4 points cardinaux. Fig. 4. Il n’y a pas de mise en évidence dans le demiant S. La grille renferme les 64 valeurs possibles du trinôme slm des 3 paramètres spin, moment cinétique azimutal, moment magnétique. L’axe NS est verseur du spin.

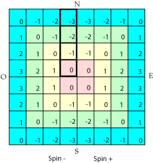
Fig. 4. La grille des moments cinétiques l et m et des spins, avec ses 64 cases. L’axe NS, trace d’un plan miroir, est verseur de spin. Grille5.ai Grille5.png

Symétries. Cette grille complète, sauf la mise en évidence qui affecte le demiant O, admet un 2e axe de symétrie miroir qui est l’axe horizontal OE, préservant le spin, orthonormal à celui verseur du spin. Jusqu’à plus amples codifications, cela suggère qu’il n’y a pas lieu de distinguer entre les rôles éventuels des quadrants NE et SE. Cela suggère aussi que le miroir axe horizontal OE lui aussi pourrait être verseur d’un paramètre analogue au moment cinétique spin.

Une case étant définie par nslm, ce paramètre ne peut être que n. Puisqu’il doit s’appliquer dès la 1^re case de toutes, où n=1, il faut que l’effet de ce verseur soit d’augmenter n d’une unité en passant du quadrant NO au quadrant SO.

L’axe EO est un miroir versant selon NS n d’une unité, de +1 dans le demiant O, (de -1 dans le demiant E).

Cette grille admet encore 2 autres symétries miroirs touchant les octants opposés en diagonales principales. Les quadrants NE et SO ne sont pas miroirs diagonaux l’un de l’autre, càd, par l’effet d’un miroir plan aligné selon SO et NE

Mais ils sont miroirs diédres l’un de l’autre, càd, par l’effet de 2 miroirs plans alignés l’un NS et l’autre OE. De même les quadrants NO et SE. (Fig. XXX à venir).

Principe 5bis. Nous posons cette exigence que l’occupation de la grille doit commencer par l’une de ces 4 cases et se poursuivre par les valeurs croissantes de m, puis de s et décroissantes de l.

Cette proposition est explicitée plus loin.

Principe 5ter. Nécessité du pairage des périodes

Peuplement. Nous rencontrons une suggestion que les périodes viennent par paires égales. Voilà pourquoi.

Paires de périodes. La grille Fig. 4 renferme 64 cases, càd autant que la population globale des 2 plus longues et dernières périodes, ayant l’une et l’autre des nombres égaux de cases, l’une et l’autre 32 cases. Cette grille renferme 12 cases J, ce qui est le double du nombre de cases J apparaissant dans une période qui en contient.

Il est assez évident qu’un exemplaire de notre grille figurative offre ce qu’il faut pour accueillir une paire de telles périodes. Le fait du pairage des périodes paraît ainsi découler inévitablement de la sorte de géométrie quantique ici proposée. On peut apercevoir une analogie de notre raisonnement en géométrie quantique avec celui concernant les projections m d’un vecteur l sur un axe qui est le champ magnétique, dans l’explication de l’effet Zeeman. Ils sont géométriques 3D l’un et l’autre ; notre raisonnement se décrit en 2D mais requiert une 3^e dimension pour effectuer l’opération du miroir ; celui concernant l’effet Zeeman requiert 3D pour sa description.

Ce pairage des périodes est examiné à nouveau plus loin.

Principe 5ter. Nous pouvons nous dispenser des écritures dans les cases de notre grille figurative et admettre que chaque case est codée selon sa position en termes de slm.

Ayant en mémoire et consultable à volonté la grille Fig. 4, voici plutôt sa répétition dans Fig. 5 en omettant les écritures dans les cases, écritures devenues redondantes par suite des synonymies avec couleurs et positions tant qu’on préserve couleurs, quadrillages et contours. Je retiens cependant les écritures de la colonne initiale en position latérale comme aide-mémoire. Fig. 5. De la sorte, l’espace à l’intérieur des cases est entièrement disponible pour y entrer les paramètres autres que slm tels que n et z.

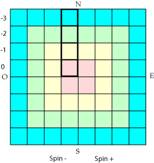
Fig. 5. La grille figurative débarrassée d’écritures dans les cases. Elle est codée. Voir texte. Espaces de la 1^re période Grille6.png Grille6.ai

Le paramètre n.

Principe 6. Un diagramme pour 2 périodes. Des tétrades d’éléments.

L’adresse du début des 2 périodes est fixée : elle doit se placer dans les spins -, donc dans le demiant O. La 1^re période débute dans le quadrant NO , la 2^e, dans le quadrant SO. Il faut ensuite choisir pour la suite de l’écriture des périodes, entre les 2 quadrants à l’intérieur du demiant E. Ou bien au même niveau, ou bien croisé. J’ai choisi croisé. Fig. 5.

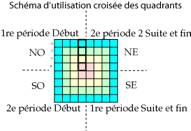
Fig. 6. Schéma d’utilisation croisée des quadrants par les 2 périodes d’une paire. Grille7.ai Grille7.png

Principe 6. Les tétrades d’éléments

Dans le diagramme, une case est vicariante de 3 autres, les 4 cases ainsi associées ont même binôme lm et appartiennent à 2 périodes. Leurs centres dessinent un carré et 2 diagonales croisées en X. On peut isoler chaque tétrade et l’afficher. Une tétrade est caractérisée par un binôme lm identiquement dans ses 4 cases, ses cases O sont spin-, ses cases E sont spin + ; ses cases NO et SE portent n1 pour la 1^re période, ses cases SO et NE portent n2=n1+1 pour la 2^e période. Voyez Fig. 7 plus bas.

Principe 7. Les cases initiales. Valeurs de n.

Nous posons qu’elles portent respectivement les valeurs n=1234. Fig. 6. (Ce choix est-il arbitraire, sera-t’il possible de le justifier par la suite ?)

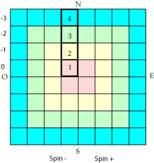
Fig. 7. Les cases initiales portant les valeurs de n. On sait la relation l<n, l et n entiers. À chaque case initiale correspond une couronne de l’une des couleurs RJVB. Grille8.png Gtille8.ai

Principe 8. Nous nous donnons 4 exemplaires de la grille figurative, ce sont les 4 strates.

Dans chaque strate nous désignons l’une des couronnes RJVB. Fig. 7.

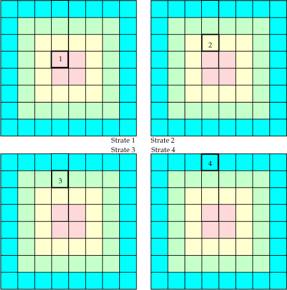
Fig. 8. Notre grille figurative apparaît ici en 4 exemplaires, des écritures ont été omises. Ce sont les 4 strates (incomplètes), chacune avec sa couronne de même numéro. Grille9.ai Grille9.png

Strate 1.

Principe 9. De construction. Le paramètre n. La construction des atomes commence par celle de z=1. Strate 1. Une condition énergétique déterminante.

Notre grille, déjà munie du trinôme slm a besoin qu’on y ajoute le paramètre n pour figurer des éléments. Avec z paramètre dépendant des 4 autres.

un élément = (slmnz) + Symbole

À cause du principe 1, la construction des atomes stables commence obligatoirement par un électron unique, soit par l‘élément H z=1, dans une case NO qui fait partie de la 1^re tétrade, comme suit. Cette tétrade s’inscrit dans les 4 cases R de la strate 1, que voilà isolée. Fig. 9.

Fig. 9. Les cases de la tétrade R dans la strate 1. Dans une case, le 1^er nombre est n, le 2^e, z. Grille12.ai Grille 12.png

Afin de continuer, il nous faut un moyen de passer à la strate 2. Ce moyen est un miroir des strates.

Strate 2.

Principe 10R. Un miroir des strates. La strate 1 envoie un miroir versant de ses cases R dans les cases R de la strate 2, en augmentant n de 2 unités dans chaque case. C’est un miroir ascendant

Ce principe découle du principe d’exclusion. Ce miroir est un plan à mi-chemin entre ceux des strates 1 et 2. Fig. 10.

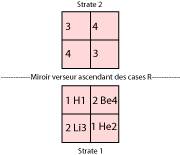
Fig. 10. De la strate 1 vers la strate 2, un miroir verseur ascendant de 2 unités s’applique aux valeurs du quantum principal n des cases R de la strate 1. Le paramètre z et les symboles restent à déterminer. Le miroir est vu élévation, les strates sont vues en projection plane.

Principe 11. La strate 2. Une condition énergétique déterminante.

La couronne J. De Fig. 8, nous isolons les cases J. Faisant suite à la 4ème case de la strate 1, la 1^re rencontrée ici est z=5 dans la colonne initiale. Remarquer l’agencement des valeurs dans la case, z à droite et n à gauche. Fig. 11.

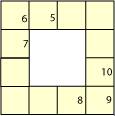
Fig.11. Les cases J de la strate 2, munies des valeurs de z... Grille14.ai Grille14.png

Ajoutons les cases R de Fig. 10. Fig. 12.

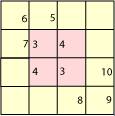
Fig.12. Les cases de la strate 2... Grille15.ai Grille15.png

La case initiale J est n=2. Quant aux cases R, elles viennent après les cases J10 et ont par suite z =11 et 12 et la case J suivante est z=13. Les 16 paramètres n et z de la strate se trouvent ainsi tous déterminés. Fig. 13.

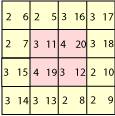
Fig. 13. ...La strate 2 complètement remplie sauf les symboles... Grille16.ai Grille16.png

Et nous ajoutons les symboles usuels. Fig. 14.

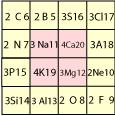
Fig. 14. ...La strate 2 complète. Grille17.ai Grille17.png

Strate3.

Principe 12RJ. Un miroir des strates. La strate 2 envoie un miroir de ses cases R et J dans les cases R et Jde la strate 3, en augmentant n de 2 unités dans chaque case. C’est un miroir ascendant.

Ce miroir est un plan à mi-chemin entre ceux des strates 2 et 3. Figs 15, 16.