ObtenirTexteXII2010

Système du Québécium.

Obtenir le tableau périodique des éléments à partir des 1ers principes.

Une tentative de géométrie quantique.

Pierre Demers.

Traduction interdite

18XII2010

Obtenir. 2118

Système du Québécium. Obtenir le tableau périodique des éléments chimiques à partir des 1ers principes. Une tentative de géométrie quantique.

Résumé. Je recommence, ayant tenté plusieurs fois depuis 1995 de formuler un cadre théorique qui expliquerait le tableau périodique des éléments dans son entier alors que l’atome de Bohr-Schrodinger ne s’applique tel quel qu’à l’hydrogène. Scerri a rappelé qu’aucun principe n’explique la suite connue de peuplement des périodes. Mon présent essai insiste sur 2 conditions s’ajoutant aux règles d’interdiction connues sur snlm et ne fait aucune référence à des conditions énergétiques. 1o Il existe d’avance une grille géométrique de cases codées à remplir, selon un trajet muni de conditions quantiques ; 2o les éléments sont associés en tétrades, règle justifiée par des associations saturantes des cônes de précession des spins. Ainsi se trouve imposée l’apparition de 4 strates de 2 périodes égales, s’accordant avec le peuplement connu des périodes. Ces conditions conduisent à la formation naturelle de la suite numérique 4, 16, 36 et 64, que j’appelle suite du québécium. On arriverait peut-être à les formuler en termes analytiques. Je suggère qu’elles sont des premiers principes, continuant ceux des mécaniques ondulatoire et quantique. La question des éléments irréguliers sera examinée à part. D‘après Réf. 1.

image2118.gif (Image GIF, 230x539 pixels)

Introduction. Avec l’addition du passage en bleu, le résumé ci-dessus reproduisant le texte soumis à l’ACFAS en 2010 pour 2011 s’applique à la présente publication. - Je rappelle d’abord des passages de publications précédentes. Puis je poursuis la recherche d’une récriture nouvelle, qui me conduit à l’énoncé de premiers principes quantiques et géométriques d’où découlerait le tableau périodique des éléments avec son peuplement connu. Des Nos 1) etc servent d’intra-références.

Pourquoi l’existence des strates? Rappel extrait de Réf. 3.

1) Dans le langage du système traditionnel, pourquoi les périodes 3, 4, 5, 6 et 7 ont-elles respectivement 8, 16, 16, 32 et 32 termes, alors que, conformément à une certaine extension du modèle de Bohr de l’atome H, la prévision est qu’elles devraient en avoir 18, 32, 50, 72 et 96? Cette prévision erronée est très loin de la réalité, et c’est peut-être pour cette raison qu’elle est rarement exposée dans la littérature; elle discrédite en quelque sorte le modèle de Bohr lorsqu’on essaie de l’appliquer aux atomes autres que H. Et encore, pourquoi, lorsqu’on observe le tableau de Mendeleev traditionnel solidement implanté partout, peut-on observer que les périodes se présentent en paires de mêmes longueurs après la 1^re , soit 8 et 8, 18 et 18, 32 et 32?

2) 1. J’ai d’abord formalisé l’affirmation empirique et j’en ai fait une règle, quitte à la justifier plus tard, et c’est mon 1^er postulat:

 «les périodes se présentent par paires d’égales longueurs », que j’appelle strates.

3) 2. Et voici mon 2^e postulat :

« la suite de éléments finit sur un gaz rare que j’ai appelé québécium, de numéro z = 118. »

4) 3. Il me fallait ajouter une remarque ou un 3^e postulat :

« pour des raisons inconnues, la règle ne s’applique pas à la 1^re strate, qui ne contient qu’une période, de 2 éléments, H et He. »

5) De la sorte, il y a 4 strates.

Je tiens pour importante la notion généralisée de strate pour assurer telle symétrie d’ensemble d’ordre 4 du tableau, afin qu’on puisse le considérer comme formé de 4 parties similaires. Il serait dificilement concevable que les 2 premiers éléments échappent à une règle aussi évidemment vérifiée dans les nombreux éléments qui les suivent. C’était ma conclusion en 1997. Réf. 5.

6) Il fallait donc impérativement corriger cette erreur de la nature, me disais-je. Un peu plus, j’aurais proclamé : « Symétrie d’abord, expérience ensuite » ! Il faut 2 périodes et 4 éléments dans la strate 1

7) J’ai tenté de placer les 2 éléments spéculatifs 119 et 120 dans une période virtuelle précédant celle contenant H et He. Cette tentative pouvant se justifier par une hypothétique nouvelle règle de symétrie, qui affirmerait que la disposition des éléments constituerait un cycle fermé sur lui même au nombre 120. Mais cette nouvelle règle paraît extravagante, car, pourquoi imposer l’idée ad hoc d’un cycle fermé

8) Et je je me trouvais confronté à une prévention que je voulais respecter, je voulais respecter une tradition qui me paraissait intouchable, remontant à Mendeleev lui-même savoir que 1^re période soit obligatoirement confinée à 2 éléments, et suivie d’une 2^e période de 8 éléments et non de 2. La tradition exigeant en outre que toute période commence par un alcalin et se termine sur un gaz rare.

9) J’ai commensé à penser qu’il n’y avait pas une erreur de la nature, mais une erreur humaine. Une erreur humaine ou disons plutôt un mauvais choix dans la représenttion du commencement du tableau.

10) J’ai connu le tableau de Charles Janet par le livre de Van Spronsen, qui le présente sans le recommander. Ce tableau créé une 2^e ligne contenant les 2 éléments Li et Be enlevés à la 2^e période traditionnelle, et qui termine ses lignes sur un élément s+, et que j’appelle invariablement un alcalino-terreux même s’il s’agit de He. Réf. 9, 10.

11) Cela m’a encouragé à passer outre à ma prévention ci-dessus et à envisager une 2^e période contenant Li et Be et des périodes se terminant sur un alcalino-terreux. Le caractère de l’élément au début d’une période varie selon la strate, il est le même pour les 2 périodes d’une strate. Une raison de symétrie supplémentaire se présente : dans une période de la nouvelle écriture, la valeur de l est fonction décroissante de z et la valeur de n est fonction croissante de z. 

12) J’ai alors modifié mon 2^e postulat et je me suis attaché à 120 pour le nombre d’éléments. Ce nombre est remarquable car il est le produit des 5 1ers nombres : 1X2X3X4X5 = 120. Regardez non les lis des champs mais les doigts de la main. Fig. 13.

Fig. 13. De ma main gauche. Le produit des 5 premiers nombres est égal à 120.

13) Le québécium perd son attrait de dernier élément de la liste, mais conserve celui de dernier gaz rare. Le dernier élément z=120 appelé officiellement et temporairement Ubn pourrait s’appeler Janetium symbole Jt.

14) Janet l’anticipateur a donc prévu dès 1928 la répartition de la suite des éléments telle que je la propose : huit lignes que j’appelle des périodes, qu’il a montrées formant des paires ayant même longueur, auxquelles il n’a pas attaché une appellation ,  que j’appelle des strates. Cela se trouve dans notre point de départ Fig. 1.

15) Reste à trouver le pourquoi des strates assurant la symétrie 4 du tableau. On l’appelle universellement périodique et elle l’est à sa manière, mais cette appellation sécurisante a peut-être empéché qu’on découvre plus tôt une réécriture convenable révélant sa symétrie. Je crois opportun de conserver l’appellation historique de système du québécium, ce qui est son nom de baptême, mais de parler au besoin de tableaux symétriques des éléments.

16) J’ai proposé en 2004 une explication fondée sur les cônes de précession virtuels des spins des électrons caractéristiques appartenant aux éléments successifs. En plus du doublage imaginé par Pauli et lié aux spins – et +, il existerait une tendance au quadruplage, 4 spins s’engageant dans une structure saturante, géométriquement identique à celle qui détermine la prolifération, si utile à la vie, des structures tétraédriques du carbone. Réf. 11, 13, 14.

17)

Fig. 14. Extrait page 17 de Réf. 13. Je propose d’attribuer un cône de précession d’ouverture 109,471o = 2arccos(1/√3) à l’électron caractéristique de chacun des éléments d’une tétrade (ici Mn, Zn, Tc, Cd). Les 4 cônes accolés avec centres communs saturent la sphère des angles solides 4pi. Cette saturation est réalisée exactement et non sensiblement comme il est écrit. Saturation ne veut pas dire remplissage. Les axes des cônes et leurs faces planes décrivent un tétraèdre aussi bien que les 4 valences égales du carbone tétraédrique.

Récriture.

Ce qui précède explique comment j’en suis arrivé à retrouver des résultats de Janet, savoir que la 1^re période doit compter 4 éléments et qu’il faut compter 8 périodes. J’ai ajouté l’intervention des équerres et des tétrades d’éléments, et proposé une explication quantique des tétrades. Afin de 1^er principe No 3. La grille cartésienne est étiquetée BVJR ou fdps dans les cases tel qu’indiqué (Fig. 3).

poursuivre nos raisonnements, je crois nécessaire de remonter en amont de l’extrait ci-dessus, soit à Réf. 5 qui a précédé Réf. 4.

NB. J’adopte souvent le style personnel du moi et du je, et je sais que le moi est haïssable, mais c’est une manière d’inviter le lecteur à réfléchir de son côté. J’ai aperçu récemment la correspondance échangée entre nos grands ancêtres Nils Bohr et Wolfgang Pauli, laquelle a contribué beaucoup à l’avancement de nos conaissances sur l’atome quantifié. C’était vers 1925, et vers la même époque paraissaient indépendamment et dans la plus grande discrétion les extraordinaires travaux de Charles Janet.

Nous cherchons des principes premiers. Nous les appellerons simplement principes. En tout premier lieu, nous acceptons les règles connues concernant les 4 nombres quantiques snlm avec leurs interdictions, on ajoute z ces 5 nombres étant inscrits dans une case numérotée z. Un élément est défini par 5 nombres zsnlm.

Principe No 1. Les règles connues concernant les 4 nombres quantiques avec leurs interdictions.

Nous savons qu’il justifie le contenu de chaque case prise isolément mais non le peuplement des périodes. Il nous faut le compléter en trouvant d’autres principes.

Construction. Une espèce atomique est définie par ce contenu d’une case z augmenté de celui des cases de 1 à z-1 non récrit par économie.

Forgeons le terme primarité pour caractériser une proposition formant un principe 1^er et examinons Fig. 1 de réf. 5, notre (Fig. 1).

18)

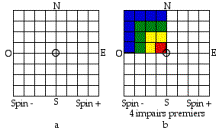
(Fig. 1) Fig. 1. a. Grille. b. Les impairs 1, 3, 5, 7 sont colorés RJVB dans le quadrant NO, image des 3 autres.

Puisqu’il s’agit de tableaux, disons que la grille vide, telle que Fig. 1a, semble s‘imposer; elle a une primarité élevée. Une grille cartésienne soit de carrés adjacents paraît un choix naturel à nous qui vivons dans un monde organisé en équerres, elle est ce que nous appelons couramment un tableau. Essayons l’énoncé suivant.

1^er principe No 2. Une grille cartésienne vide de cases carrées vides...

Mais est-il bien vrai qu’elle s’impose à priori? Le tableau périodique traditionnel est inscrit dans un quadrillage 2D, mais chaque période y occupe un agencement linéaire 1D. Il n’utilise la 2^e dimension que par des retours à la ligne à la fin de chaque période. Notre grille cartésienne admet plutôt qu’une période puisse y occuper plus qu’une dimension. La grille est en principe indéfinie mais il nous suffira des 16 cases du quadrant NO, ce qui me conduit à compléter l’énoncé comme suit.

Principe No 2. Une grille cartésienne de 16 cases carrées vides.

Ces cases placées dans le quadrant NO du plan orienté avec origine marquée. (Fig. 2)

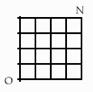
(Fig. 2) Principe No 2. Une grille cartésienne de 16 cases carrées vides.

Dans la Fig. 1b, je choisis d’assigner à une colonne de 4 cases un rôle de principe No 3. 1^er principe No 3. La grille cartésienne est étiquetée BVJR ou fdps dans les cases tel qu’indiqué (Fig. 3).

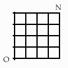
On peut trouver meilleure primarité. Par exemple, dans (Fig. 2) qui est un extrait de ma 1^re version en ligne de Québécium International Réf. 6.

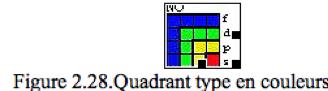
(Fig. 2) Fig. 2.28 présente dans QbInterna2.3.html Réf. 6.

Le quadrant NO de (Fig. 1b) reproduit (Fig.2). Mais même ce quadrant isolé ne me satisfait encore pas comme 1^er principe. Il contient une suite verticale des 4 cases BVJR ou fdps et c’est cette suite que je choisis comme 1^er principe No 3.

Remarquer que les cases porteuses de ces étiquettes sont de spin-.

Références.

Réf. 6. Pierre Demers 2001, Système du Québécium, 1^re version en ligne. http://www.lisulf.quebec/QbInterna..BONJOUR.html, voyez Réf. 2.

Réf. 5. 1014 Pierre Demers 2009, Système du Québécium. Des états de l'hydrogène aux éléments du tableau. 4IV2009.1 DesEtats5bis.htm

Réf. 4. 1015 Pierre Demers 2009, Système du Québécium. Confection du tableau des éléments par écriture des valeurs de n. 4IV2009.2 Cconfectab.htm

Réf. 1. Pierre Demers 2010, Système du Québécium. Obtenir le tableau périodique des éléments chimiques à partir des 1ers principes. Une tentative de géométrie quantique, Résumé No 2118 d’un projet de communication à l’ACFAS 79^e congrès, Univ. de Sherbrooke juin 2011

Réf. 2. . http://www.chem.ucla.edu/dept/Faculty/scerri/, http://www.lisulf.quebec/quebecium.htm, 1026, 1025, 1015, commentaires etc.

Réf. 3. http://www.lisulf.quebec/EquerreJanetSc.htm