Système du Québécium.
Aux 5 solides de Platon, faudrait-il en ajouter un 6e?
Pierre Demers
Québécium International
XVIe congrès international de Biomathématique, Versailles, 3 et 4 septembre 2001*
Un monde virtuel du Québécium 3D. Le monde virtuel 2D du résumé précédent peut se transformer en un monde virtuel 3D. Pour cela, il faut remplacer les cases par des boules et les assembler en un empilement de moindre encombrement. Cet empilement dessine une pyramide à base triangulaire ou un tétraèdre régulier. Les strates se superposent avec les nombres magiques indiqués, donnant des formes tétraédriques de 4, 20, 56 et 120 boules. 120 boules constituent le monde virtuel du Québécium 3D.
Les boules ne remplissent pas complètement l'espace. Un solide circonscrit peut remplacer chaque boule, il doit avoir 12 faces planes qui sont des losanges dont les axes sont entre eux comme 2
1/2. Ce solide est le rhombododécaèdre. Il a 12 faces égales et mérite l'appellation de solide homoédrique. Il s'inscrit dans un cube.Le rhombododécaèdre. Ce solide a de quoi retenir notre attention. Il permet de constituer le monde virtuel du Québécium 3D, d'intérêt biomathématique. Indépendamment de cette capacité, il possède une autre capacité proprement géométrique : celle de paver l'espace 3D, c'est-à-dire, de l'occuper sans interstice et sans chevauchement par sa répétition. En occupant cet espace, il trace naturellement un tétraèdre régulier. Aucun autre solide ne possède cette capacité.
Deux solides homoédriques pavent l'espace : le cube et le rhombododécaèdre.
Remarquons qu'il est homoédrique, c'est-à-dire que ses faces sont toutes égales avec des arêtes toutes égales. Les angles dièdres formés par ses faces sont tous égaux, valant 120
o. Il n'est cependant pas un solide régulier de Platon, parce que les angles plans de ses faces ont 2 valeurs et non une seule et ses sommets sont de 2 sortes et non d'une seule, triédriques et tétraédriques. Il possède une affinité avec le dodécaèdre régulier solide de Platon, qui a lui aussi 12 faces, qui sont pentagonales.Voici un sommaire de ces 2 solides. Ils satisfont l'un et l'autre à la relation de Gauss.
2+A = F+S
A nombre d'arêtes, F nombre de faces, S nombre de sommets.
| Sommaire | Rhombododécaèdre |
Dodécaèdre de Platon |
| F faces |
12 | 12 |
| Faces | Losanges |
Pentagones |
| A arêtes | 24 | 30 |
| S sommets |
14 | 20 |
| S tétraédriques |
6 | 0 |
| S triédriques |
8 | 20 |
| Angle dièdre entre les faces | 120o |
122 o,6 |
| Angle prismatique entre les grandes diagonales consécutives |
90 o |
Les grandes diagonales se rencontrent aux sommets tétraédriques et forment entre elles deux angles droits. Leur enchaînement détermine trois carrés sur les faces du rhombododécaèdre. Ces carrés sont congruents à trois prismes de base carrée. Pour cette raison, nous appellerons angles prismatiques les angles droits en question.. Il n'y a rien de tel dans le dodécaèdre de Platon.
Ces trois carrés délimitent 8 faces triangles équilatéraux formant un octaèdre inscrit dans le rhombododécaèdre
Solides et tubes. Une propriété remarquable du rhombododécaèdre est son aptitude à passer au dodécaèdre de Platon. Ce passage s'illustre commodément si on remplace les faces par leurs arêtes et les arêtes par des tubes. Les tubes sont retenus par des cordes élastiques.
Pour passer du rhombododécaèdre au dodécaèdre de Platon, on remplace chaque sommet tétraédrique par une arête nouvelle et 2 sommets triédriques. Le nombre de sommets tétraédriques passe de 6 à 0, le nombre de sommets triédriques passe de 8 à 20. Le nombre total S de sommets passe de 14 à 20. Dans l'équation de Gauss (2+A = F+S), au lieu de
2+24 = 12+ 14 rhombododécaèdre
on a
2+30 = 12+20 dodécaèdre de Platon
Le nombre de faces F reste constant et égal à 12. Pour passer du dodécaèdre de Platon au rhombododécaèdre, on suit le chemin inverse.

De 4 à 5 arêtes, d'un sommet tétraédrique à 2 sommets triédriques et réciproquement.,
Cristaux de symétrie 5. La cristallographie classique interdit les cristaux de symétrie 5, par exemple ceux qui seraient formés de dodécaèdres de Platon. Cependant on en réalise, à en juger par les formes extérieures et par la diffraction des rayons X. Par ailleurs, le rhombododécaèdre est une forme admise en cristallographie, rattachée au système cubique et réalisée notamment dans les grenats et dans le chlorure d'ammonium, Étant donné les affinités entre le dodécaèdre de Platon et le rhombododécaèdre, on est en droit d'espérer que l'étude de ce dernier éclairera le poblème posé.
Une nouvelle classe de solides, les solides homoédriques. On peut constituer une nouvelle classe de solides, celle des solides homoédriques. Elle renferme 6 solides et seulement 6 : les 5 réguliers de Platon et le rhombododécaèdre décrit.
Rappelons qu'en 1809, Poinsot découvrait les 4 solides réguliers à faces convexes (4 dodécaèdres et un icosaèdre). Il montrait que les 5 solides réguliers traditionnels appartiennent à une classe plus étendue. L'extension proposée ici est différente.
Format A4. Le format A4 et les autres formats de papier A0, A1, etc se prêtent particulièremnt à la réalisation de rhombododécaèdres. En effet, le rapport hauteur sur largeur dans le format A4 vaut 29,7cm/21cm =2
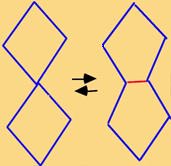
1/2 ; par suite, pour le losange inscrit, le rapport des diagonales a la même valeur. Des feuilles A4 ou de telles feuilles pliées deux fois en deux, donnant le format A6, sont faciles à découper à vue en losanges inscrits. Puis on assemble les losanges avec du ruban adhésif 4 par 4 en réunisant leurs sommets aigus. Il faut deux tels assemblages. À l'un d'eux, on ajoute 4 losanges selon la figure, puis on lui ajoute l'assemblage non augmenté. Alors, on a 12 losanges qui forment une structure qui a du corps. et qui résiste à la déformation.Il existe donc une affinité entre le format A4 et le rhombododécaèdre, et par suite entre le même format et le système du Québécum.
Fondé en nature. On a des raisons de penser que le format A4 est fondé en nature : il apporte cette satisfaction instinctive, toute naturelle, de retrouver la même forme par pliage en deux, puis en 4, etc, et on peut voir là une raison de son succès en Europe. Cette satisfaction est liée à un principe de conservation, conservation de la forme lors du pliage. Ainsi s'établit une analogie fondamentale entre ce format et le système du Québécium, remarquable pour les symétries et les groupes de conservation qu'il présente. Une manière de conclure est de dire que le système du Québécium, lui aussi, est fondé en nature.


Les étapes, du losange A4 au rhombododécaèdre.
Réf. Pierre Demers :
Système du Québécium. De l'atome d'hydrogène à l'être humain, une continuité biomathématique. Le résumé précédent.
Réf. F. Collot, S. I. Biomathématique, 4, rue Mayet, 75006 Paris, France 33 1 45 67 79 17
*NB. Le congrès a été remis pour des raisons d'organisation.. Ceci est le texte remanié au 12 octobre 2001.