QbEllipseBiomath.html
Système du Québécium
Le tableau elliptique des éléments
Pierre Demers, Professeur honoraire de l'Université de Montréal
D'après une communication au XIXe Colloque international de Biomathématique, Versailles, 9 et 10 septembre
2004Résumé
Mise à jour du système du Québécium appliqué à la classification des éléments. Après une formulation du système du Québécium dans la théorie des ensembles de Cantor, présentation de deux résultats nouveaux. On montre, grâce au principe de quadrature, comment la succession des éléments arrêtés au nombre de 120, dérive de la succession des états de l'hydrogène excité, dérivation qui est restée jusqu'ici conjecturale et impossible à justifier. On montre ensuite comment la nouvelle classification, avec ses symétries rigoureuses mettant en évidence le nombre quatre important en biomathématique, aboutit à la forme avantageuse d'une ellipse et à un tableau quart d'ellipse de 30 cases.
http://www.lisulf.quebec/quebecium.html, www.quebecium.qc.ca
Entre biomathématique et tableau des éléments, quelles relations?
La matière de tous les êtres vivants, aussi bien que la matière de l'univers inanimé qui nous entoure, est formée d'un nombre limité d'éléments, présents sous la forme d'atomes et de molécules. Déjà à ce seul titre, le tableau des éléments mérite l'attention des biomathématiciens aussi bien que des chimistes, puisque la vie n'existe pas sans un support matériel. Louis-Marie Vincent précisait cela dans les pages de Biomath 2003, XXXX, No 158, p. 17 : parmi les 9 propriétés définissant la vie, il place "échanges... flux de matière".
Mais il y a plus. Également dans les pages de Biomath, on trouve la description, sous le titre de Système du Québécium, des similitudes mathématiques remarquables que j'ai mises en évidence entre le tableau des éléments et un tableau original que j'ai proposé des biomolécules essentielles au processus de la synthèse des protéines, codons et acides aminés. Voyez Biomath depuis 1997.
Voici une mise à jour sur le système du Québécium appliqué à la classification des éléments. Deux résultats nouveaux. On montre d'abord comment la succession des éléments arrêtés au nombre de 120, de z = 1 à z = 120, dérive logiquement de la succession des états de l'hydrogène excité, dérivation qui est restée jusqu'ici conjecturale et impossible à justifier. Elle est rendue possible par l'application d'un principe de quadrature, en plus d'effets : celui de Pauli et celui de Zeeman. On montre ensuite comment la nouvelle classification, avec ses symétries rigoureuses, aboutit à la forme avantageuse d'une ellipse.
Une mise à jour des applications aux biomolécules fait l'objet d'un article distinct.
Le présent article reprend les innovations décrites dans mon site internet et dans un livre récent et y ajoute.
www.quebecium.qc.ca
Système du Québécium. La nouvelle classification des éléments, par Pierre Demers, PUM2004.
Correspondances entre la théorie de l'hydrogène et la théorie des éléments.
Trois principes : Pauli, Zeeman, quadrature.
L'atome d'hydrogène n'est pas une succession d'atomes ou d'éléments, mais un atome unique ayant un seul électron. Il a cependant une succession, celle de ses états excités dont la description spectroscopique se fait au moyen des mêmes variables quantiques qui définissent les caractères des atomes, ou du moins de trois d'entre elles : s, n et l; m n'intervenant pas. Les caractères des atomes sont des états électroniques.
Il est donc indiqué de chercher des correspondances entre ces deux successions. Pour la commodité du langage :
état excité se rapporte à l'atome d'hydrogène : H1. H2, etc;
état électronique se rapporte au caractère électronique des atomes : z1. z2, z3 etc.
Les correspondances qui apparaissent immédiatement sont très imparfaites. Les correspondances exactes ici présentées font intervenir physique et géométrie.
D'une part deux principes de physique atomique connus, auxquels nous donnons des noms originaux : effet Pauli et effet Zeeman.
Et d'autre part un principe nouveau, de nature géométrique, que nous appelons effet de quadrature.
Effet Pauli touchant les états s, l = 0. Un état s de l'hydrogène atomique est unique, il est défini par s = 0 et l = 0. Mais sa correspondance dans la succession des atomes est double : s = ±, le spin peut être d'un signe ou de l'autre. Nous appellerons cette circonstance l'effet Pauli. Un état s donne naissance à 2 éléments, de spins ±.
Effet Zeeman ou de multiplet touchant les états non s, l > 0. Un état autre que s de l'hydrogène atomique possède un spin - ou + et une valeur de l autre que 0. Sa correspondance dans la succession des atomes est multiple, le quantum magnétique m pouvant prendre 2l+1 valeurs : 3, 5 ou 7. Un état non s de l'hyrogène est soit de spin -, soit de spin + et correspond à 3, 5 ou 7 éléments. La multiplicité est 3, 5 ou 7.
Effet de quadrature. Afin de l'appliquer, nous nous donnons une grille indéfinie justifiée à l'origine. Comme Francis Collot me l'a suggéré, c'est l'occasion de recourir à la théorie des ensembles de Cantor et celle-ci peut aider à suivre les raisonnements proposés.
Application de la théorie des ensembles à l'effet de quadrature
La grille est un ensemble comprenant des cases comme "objets". Nous réservons le mot "élément" aux éléments chimiques.
cases
C grilleLes cases sont contenues dans la grille, la grille est un ensemble composé de cases. On peut y déterminer des sous-ensembles de deux manières qui nous seront utiles : A. en couronnes puis en équerres, ou bien B. en quadrants puis en équerres. Dans les deux manières, les équerres apparaissent comme étapes intermédiaires entre l'ensemble général qu'est la grille et les objets ultimes que sont les cases.
On le voit, parler de la présence des objets ne suffit pas. Les positions mutuelles des objets importent. Nos objets sont des cases agencées dans une grille.

Fig. 1. Une grille indéfinie, ensemble d'objets qui sont des cases. Ces cases sont pourvues de relations mutuelles.
A. Division de la grille en couronnes et équerres.
A1. On se donne l'ensemble général des cases étendu indéfiniment selon ±x et ±y. Fig. 1
Nous y déterminons des couronnes concentriques centrées sur l'origine, contenant 4, 12, 20, 28 cases etc. Les couronnes de 12 cases et plus entourent un espace central qui ne leur appartient pas. Ce que nous appelons couronne de 4 cases n'enferme évidemment aucun tel espace. L'ensemble des cases peut s'appeler ensemble des couronnes.
couronnes C grille
La grille est composée de couronnes en nombre indéfini.
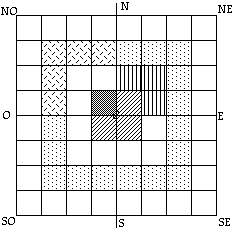
Fig. 2. Exemple d'une couronne de 20 cases et d'une équerre de 5 cases; d'une couronne de 4 cases et d'une équerre d'une case; d'un quadrant de 9 cases; d'une strate de 36 cases.
A2. Les sous-ensembles des équerres composant les couronnes. Chacune de ces couronnes se divise en 4 quarts désignés par les points cardinaux intermédiaires NO, SO, SE, NE, ces quarts renfermant selon le cas 1, 3, 5, 7 cases etc. Ces quarts sont des équerres symétriques. Les équerres de plus d'une case ont deux bras égaux d'une, de deux, trois cases etc. Les équerres d'une case n'ont pas de bras ou encore, disons qu'elles ont des bras nuls.
équerres C couronne
Une couronne est composée d'équerres au nombre de 4. Fig. 2.
A3. Les sous-sous-ensembles des cases composant les équerres. Chacune des équerres comprend 1, 3, 5, 7 cases etc. Par géométrie, le nombre des cases dans une équerre est impair.
cases C équerre
Une équerre est composée de cases en nombre impair.
B.Division de la grille en quartiers et équerres.
B1. L'ensemble général des cases. Identique à A1. Nous y déterminons 4 quartiers de 90o limités par les axes ±x, ±y, désignés par les points cardinaux intermédiaires NO, SO, SE, NE. Ces quartiers ont une étendue indéfinie et chacun peut se diviser en équerres symétriques.
quartiers C grille
La grille est composée de quartiers au nombre de 4.
B2. Les sous-ensembles des équerres composant les quartiers. Le nombre d'équerres dans un quartier est indéfini.
équerres C quartier
Un quartier est composé d'équerres en nombre indéfini.
B3. Les sous-sous-ensembles des cases composant les équerres. Identique à A3.
cases C équerre
Une équerre est composée de cases en nombre impair.
Ne pas confondre quartier et quadrant.
Quadrants et strates
Une notion utile est celle de quadrant, associée à celle d'équerre. C'est le carré occupé par une équerre et les autres cases, s'il en est, situèes entre cette équerre et l'origine. Un quadrant est défini par un nombre de cases : 1, 4, 9, 16, 36 etc et par l'un des points cardinaux intermédiaires NO, SO, SE ou NE. Les nombres de cases sont la suite des carrés d'entiers.
Une strate se compose des 4 quadrants ayant même nombre de cases. Les strates comprennent 4, 16, 36, 64 cases etc. Ces nombres sont la suite des carrés des pairs.
Correspondances en l'absence du principe de quadrature
Le problème des correspondances est exprimé dans le Tableau 1, rassemblant les données sur les états excités H1, H2, H3 etc et les états caractéristiques z1, z2, z3 etc, chacun de ces derniers états représentant un élément z. Comme il d'agit d'une mise en ordre, seuls les numéros d'ordre nous importent.
Ce tableau applique les principes de Pauli et de Zeeman et le résultat est intéressant.
On reconnaît que chacun des états z est en correspondance avec un état H. Ces correspondances sont intéressantes, mais imparfaites puisque les éléments, s'ils se présentent tous, ne se présentent pas dans l'ordre voulu. Immédiatement après z1 et z2, surviennent z5, z6, z7 alors qu'on attend z3 et z4. Immédiatement après z10 on rencontre z13, z14, z15 alors qu'on attend z5 et z6 qui précèdent. Etc.
Le résultat présente des interversions et nous allons voir que le principe de quadrature permet de les résoudre.
Tableau 1. Les données sur l'atome d'hydrogène
.Au moins deux états z correspondent à chaque état H.
Effet Pauli : deux. Effet Zeeman ou de multiplet : trois, cinq ou sept.
En gras : états amorçant une strate.
États H
............États zH1
......1s..........-1s0 +1s0....................................................z1 z2H2
......-2p......-2p-1 -2p0 -2p1.......................................z5 z6 z7H3
......2s.......-2s0 +2s0...................................................z3 z4H4
......+2p......+2p-1 +2p0 +2p1.....................................z8 z9 z10H5
......-3p......-3p-1 -3p0 -3p1......................................z13 z14 z15H6
......3s......-3s0 +3s0...................................................z11 z12H7
......-3d......-3d-2 -3d-1 -3d0 -3d1 -3d2......................z21 z22 z23 z24 z25H8
......+3p......+3p-1 +3p0 +3p1.....................................z16 z17 z18H9
......+3d......+3d-2 +3d-1 +3d0 +3d1 +3d2...................z26 z27 z28 z29 z30H10
.....-4p......-4p-1 -4p0 -4p1......................................z31 z32 z33H11
......4s......-4s0 +4s0..................................................z19 z20H12
......-4d......-4d-2 -4d-1 -4d0 -4d1 -4d2....................z39 z40 z41 z42 z43H13
......+4p......+4p-1 +4p0 +4p1....................................z34 z35 z36H14
......4f......-4f-3 -4f-2 -4f-1 -4f0 -4f1 -4f2 -4f3..........z57 z58 z59 z60 z61 z62 z63H15
......+4d......+4d-2 +4d-1 +4d0 +4d1 +4d2.................z44 z45 z46 z47 z48H16
......+4f......+4f-3 +4f-2 +4f-1 +4f0 +4f1 +4f2 +4f3....z64 z65 z66 z67 z68 z69 z70H17
......5p......-5p-1 -5p0 -5p1......................................z49 z50 z51H18
......5s......-5s0 +5s0.................................................z37 z38H19
......+5p......+6p-1 +6p0 +6p1...................................z52 z53 z54H20
......-5d......-5d-2 -5d-1 -5d0 -5d1 -5d2....................z71 z72 z73 z74 z75H21
......+5d......+5d-2 +5d-1 +5d0 +5d1 +5d2................z76 z77 z78 z79 z80H22
......-5f......-5f-3 -5f-2 -5f-1 -5f0 -5f1 -5f2 -5f3.......z89 z90 z91 z92 z93 z94 z95H23
......+5f......+5f-3 +5f-2 +5f-1 +5f0 +5f1 +5f2 +5f3...z96 z97 z98 z99 z100 z101 z102H24
......-6p......-6p-1 -6p0 -6p1....................................z81 z82 z83H25
......6s......-6s0 +6s0................................................z55 z56H26
......+6p......+6p-1 +6p0 +6p1...................................z84 z85 z86H27
......-6d......-6d-2 -6d-1 -6d0 -6d1 -6d2....................z103 z104 z105 z106 z107H28
......+6d......+6d-2 +6d-1 +6d0 +6d1 +6d2.................z108 z109 z110 z111 z112H29
......-7p......-7p-1 -7p0 -7p1.....................................z113 z114 z115H30
......7s......-7s0 +7s0.................................................z87 z88H32
......+7p......+7p-1 +7p0 +7p1...................................z116 z117 z118H33
......8s......-8s0 +8s0..................................................z119 z120Source des données : http://physics.nist.gov/cgi-bin/AtData/display.ksh?XXE0qHqIXXT2XXI
Intervention du principe de quadrature
Le principe de quadrature est plus facile à appliquer qu'à formuler. Voici un essai de formulation, sous la forme de règles successives. L'appellation quadrature et le nombre 4 sont liés à la présence de 4 quartiers dans la grille.
Nous procédons dans l'ordre des états H. Nous cherchons à réaliser un tableau des éléments caractérisés par leur numéro d'ordre z.
Tout d'abord : nous dirons qu'un état excité H "donne naissance" à plusieurs états ou éléments z, ces éléments formant des groupes de 1, 3, 5 ou 7. Les groupes sont d'un signe de spin ou de l'autre. Ainsi le 1er état H donne naissance à deux groupes, le 2e, à un seul. Dans le langage habituel des chimistes, ces groupes sont des demi-blocs s, p, d ou f.
R1. Équerres, indivisibilité des équerres. Chaque groupe figure par une équerre indivisible.
1re grille, 1re strate. Dans une 1re grille indéfinie, on place l'équerre z1 dans le quartier NO, dans la case touchant l'origine. Ce choix est de convention. L'équerre z2 ira dans la case symétrique SE.
Ainsi se trouve amorcée une strate de 4 cases. Fig. 3.
R2. Règle d'amorçage. Une strate amorcée doit être complétée en priorité avant de procéder à remplir une strate suivante.
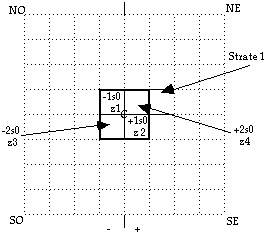
Fig. 3. Strate 1. La strate 1 est définie par le placement de -1s0 et +1s0 et ne peut être complétée que par -2s0 et +2s0.
Il suit que l'équerre z5, z6, z7 issue de H2 ne peut prendre place dans la strate 1 pour cause de manque d'espace et d'indivisibilité.
Il suit qu'il faut chercher plus loin dans le Tableau 1 et choisir une paire d'équerres d'une case donc issues d'un état s de l'hydrogène, soit de H3.
Ainsi, nous avons résolu une première interversion : z3 et z4 précèdent z5, z6 et z7. La logique apportant solution en est une de symétrie.
z3 ira dans le quartier SO et z4, dans le quartier NE.
2e grille, 2e strate. Il nous faut disposer d'une 2e grille pour la suite. Ce sera la 2e strate. Elle s'amorce avec l'équerre z5, z6, z7 issue de H2, qui se place dans le quartier NO. Cet amorçage détermine une strate de 16 cases. On note que cette équerre est de spin -.
R3. Partenariat d'orbitales. Une équerre étant placée dans un quartier, l'équerre partenaire d'orbitales doit être placée en priorité dans le quartier symétrique par rapport à l'origine.
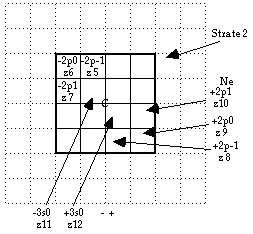
Fig. 4. Installation d'une équerre -2p et apparition de la strate 2. On ajoute l'équerre +2p opposée et on complète les 2 quadrants opposés.
Il suit qu'il faut d'urgence trouver l'équerre semblable à la précédente sauf le signe du spin. C'est z8, z9, z10 issue de H4. Fig. 4
R4. Les paires de quadrants. Des quadrants opposés par rapport à l'origine une fois amorcés forment une paire qui doit être remplie avant de procéder au remplissage de l'autre paire.
Il suit qu'il faut trouver de quoi remplir les 2 cases encore vides dans la figure 4 et ce sera z11 et z12.
Une équerre étant placée, l'équerre opposée doit être placée en priorité.
Le remplissage d'une paire de quadrants opposés, une fois amorcé, doit être complété avant d'amorcer celui d'une autre telle paire de quadrants dans la même strate.
Lorsqu'une strate est complétée, on procède dans une nouvelle grille.
Notre principe de quadrature fait de 4 un nombre magique de la structure des atomes.

Fig. 5. Strate 3. Les équerres -3d et +3d sont en place, il faut ajouter les équerres de l'encadré. etc.
La suite des raisonnements est de la même sorte jusqu'à z = 118 et 120 et conduit à créer les strates 3 de 36 cases et 4 de 64 cases sans besoin de règles supplémentires. Fig . 5
On note que, de deux états H p, d ou f, celui de spin - se présente invariablement avant celui de spin +, en accord avec notre règle de placer la première équerre dans un quadrant est.
La suite des raisonnements est de la même sorte et fournit la classification nouvelle dans sa version 2, selon la nomenclature du livre mentionné. Dans cette version, il n'y a aucune case vide.
L'actuel résultat propose une définition nouvelle des périodes : elles se terminent avec 2 éléments s. Les fins de périodes sont ainsi : He, Be, Mg, Ca, Sr, Ba, Ra, élément 120. Les propriétés chimiques ne sont pas affectées pour autant, la structure des gaz rares conserve son rôle bien connu, mais les périodes ne se terminent plus sur un gaz rare sauf la 1re.
De la sorte, la version 2 renferme 8 périodes complètes. Fig. 6.
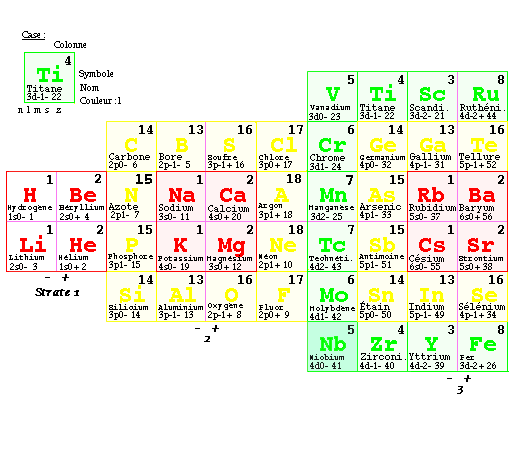

Fig. 6. Système du Québécium. La nouvelle classification des éléments, version 2, dérivant d'une comparaison avec les états de l'atome d'hydrogène. Quatre strates, deux périodes par strate, 120 éléments. Huit périodes se terminant chacune sur un élément +s0.
Principe de quadrature : analogies cristaux et protéines
L'opération virtuelle de synthèse de 4 strates ordonnées peut s'envisager comme une opération sur un système au sens général du mot. Il y a d'une part un bassin d'états disponibles et d'autre part une force organisatrice de ces états, qui croissent acquérant une configuration particulière, celle du tableau version 2 avec ses quatre strates carrées distinctes formées chacune de pluieurs couronnes emboîtées. La force obéit à une quadrature.
La croissance des trémies de sel marin est analogue. Elle aussi conduit à la réalisation, concrète celle-ci, de couronnes carrées successives et procéde à partir d'un bassin liquide avec sélection des ions qu'il contient. Ces couronnes sont superposées, donnant l'aspect d'ne pyramide quadrangulaire, creuse parce qu'il n'y a qu'une couronne par niveau. L'un de ces carrés n'augmente pas indéfiniment : il apparaît une règle de saturation de chaque niveau, analogue à nos strates et quelque chose qui ressemble à une force de quadrature.
http://geosciences.geol.u-psud.fr/ObjectifTerre/Sedimentologie/Guerande/saline/oeillets/oeilletsel.htm "Guérande très connu pour son sel et la fleur de sel". Merci à Christian Emig pour cette référence.
Le tableau version 2 devient une pyramide quadranguaire pleine si on superpose les strates composées de blocs cubiques représentant les cases.
La croissance d'une molécule de protéine est analogue en ce qu'elle procède à partir d'un bassin fournisseur d'atomes, molécules et ions sur lesquels s'exercent des forces de sélection et d'organisation. La molécule n'est pas carrée mais a une forme spécifique.
Classification elliptique. Version 3
Par des translations de cases choisies selon l'axe OE des x, la version 2 prend un aspect symétrique selon cet axe dans son tout. Elle devient la version 3.
En théorie des ensembles : les 120 cases forment un ensemble, chaque strate en est un sous-ensemble. Trois de ces sous-ensembles, soit les strates 1, 2 et 3, sont partagées en moitiés 1O et 1E, 2O et 2E, 3O et 3E qui sont des sous-sous-ensembles, lesquels subissent des translations ouest vers est. Finalement, les 6 sous-sous-ensembles se répondent deux à deux dans une symétrie miroir par rapport à l'axe NS central :
1O avec 1E; 2O avec 2E; 3O avec 3E
La strate 4 reste inchangée. Les symétries qui existaient par rapport à l'origine des strates au sein de chaque strate avant la translation deviennent des symétries par rapport à l'origine de la figure polygonale du tout.
Et voilà la version 3 de la classification nouvelle. La figure polygonale s'inscrit par 8 de ses 16 sommets dans une ellipse dont les demi-axes sont entre eux comme 10,33/4,33, l'unité étant le côté des cases. L'ajustement de cette ellipse est tel qu'on ne peut pas y loger une seule case supplémentaire.
Un intérêt théorique de cette version est qu'elle conserve la symétrie quaternaire des cases lm, décrite à la figure 7 : cette symétrie existe aussi bien que le centre C soit celui d'une strate ou le centre du tout. Fig. 7
Un autre intérêt théorique de cette version est davantage chimique : elle sépare les spins, - à l'ouest, + à l'est : hydrogène et alcalins sont à l'ouest, hélium, alcalino-terreux, halogènes et gaz rares à l'est.
Classifications elliptiques 3/2 et 3/4
Version demi- ellipse 3/2. Les symétries NS et EO de la version elliptique 3 de 120 cases se prêtent à une condensation par pliage en deux conduisant à un tableau de 60 cases contenant chacune 2 éléments. La ligne de pliage peut être l'axe NS ou l'axe OE.
Pliage autour de l'axe NS. Chaque case renferme deux éléments semblables par l et m mais l'un n et l'autre n+1 avec des signes de spin différents. C'est l'équivalent de faire passer le format de A4 à A5.
Pliage autour de l'axe OE. Chaque case renferme deux éléments semblables par s, l et m mais l'un n et l'autre n+1. Au-delà de n = 1, ces éléments sont de la même famille chimique.
Version quart d'ellipse 3/4. Cette fois, le pliage se fair successivement selon deux lignes, l'axe NS et l'axe OE et donne un tableau de 30 cases de 4 éléments chacune, appartenant à la même tétrade. C'est l'équivalent de faire passer le format de A4 à A6. Alors se trouvent rassemblées les 30 tétrades de la classification, chacune étant définie par un binôme lm et pourvue de symétries quaternaires que voilà une fois de plus démontres. Figs 8, 10, 11.
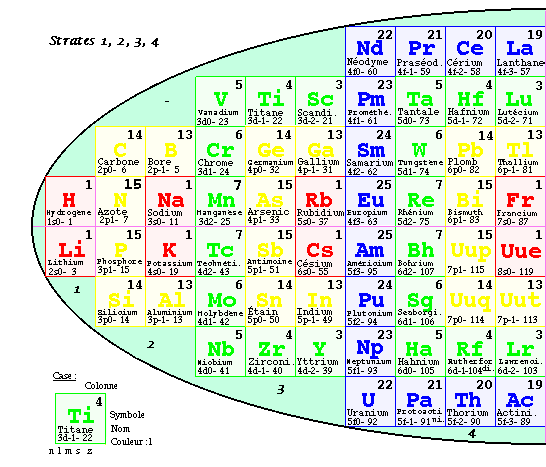
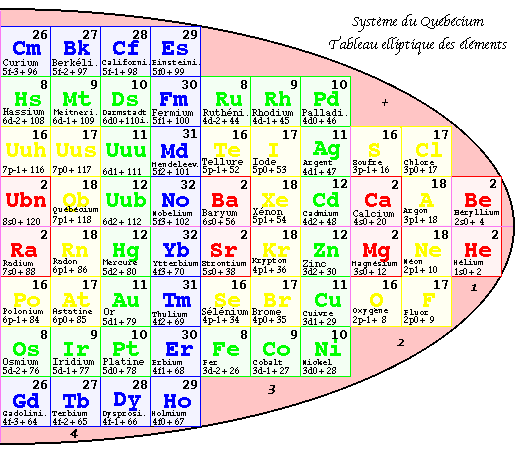
Fig. 7. Version 3 de la nouvelle classification. Tableau elliptique des éléments. Spins - moitié ouest et + moitié est.
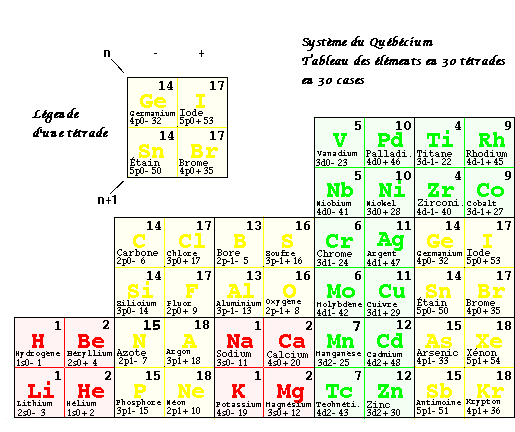
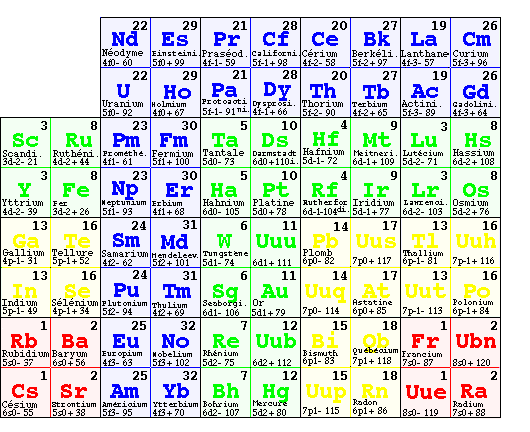
Fig. 8. Version 3/4 de la nouvelle classification. Tableau quart d'ellipse. Une tétrade par case. Spins - moitié ouest et + moitié est de chaque case.
Il est intéressant de réaliser une forme de la version quart d'ellipse en pyramide quadrangulaire. À cette fin, on remplace les cases planes par des blocs cubiques qu'on empile. Vue en projection plane, on y aperçoit 16 colonnes de blocs représentant chacun une tétrade.
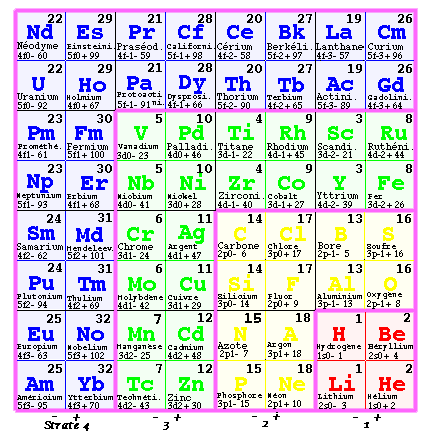
Fig. 9. Version quart d'ellipse en blocs cubiques superposés dessinant une pyramide quadrangulaire. Vue en projection plane.
On peut y lire les numéros traditionnels désignant les familles d'éléments allant de 1 à 32. Une famille apparaît deux fois dans chaque colonne. La moitié gauche de la colonne renferme deux fois une famille, la moitié gauche renferme deux fois une autre famille; entre les numéros de ces familles, la différence est l+1. L'hydrogène commence la famille 1, l'hélium commence la famille 2. Fig. 9
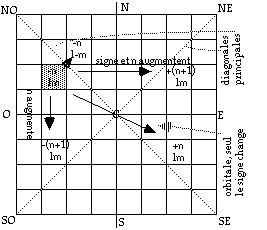
Fig. 10. Toute case possède 3 cases symétriques avec conservation de l et m, illustration pour une case -nlm. Elle forme ainsi une tétrade lm. Toute case appartient à une tétrade lm, contenant les 4 permutations du signe et de n. De plus, elle possède à l'intérieur d'une strate une case symétrique par changement du signe de m, sauf si elle est située sur une diagonale principale de sa strate. Ce qui précède est vrai à l'intérieur d'une strate de la version 2 ou dans le tout de la version 3, C étant l'origine.

Fig. 11. L'une des 30 tétrades dans les cases de la version 3/4 tableau quart d'ellipse. Le quantum principal n vaut 1, 3, 5 ou 7.
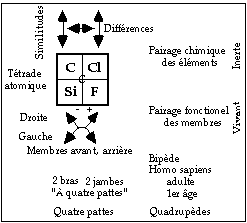
Fig. 12. Pairage virtuel chez quatre éléments d'une tétrade. Pairage chez les vivants.
Analogies avec les quadrupèdes
Dans les tétrades, on observe pairage, les propriétés chimiques sont semblables à l'intérieur d'une paire de même spin et différentes lorsqu'on passe d'une paire à l'autre. En bref, il y a similitudes verticalement et différences horizontalement. C'est notoirement le cas de la tétrade renfermant C, Si, Cl et F. C et Si, de spin -, se ressemblent chimiqument et ne ressemblent pas du tout à Cl et F. Cl et F de spin +, se ressemblent étant halogènes puissants. Figs 11, 12
D'autres tétrades n'ont qu'un pairage faible, les différences entre les 4 éléments, par exemple Cr, Mo, Ag et Cu sont tous des métaux. Il y a donc des degrés dans le pairage selon les tétrades.
Or une vérité biomathématique banale mais indéniable est la présence de 4 membres chez les quadrupèdes et chez le bipède Homo sapiens. Cette vérité, basée sur le nombre 4, pourrait s'appeler quadruplicité et présente une analogie avec la quadrature des tétrades. Fig. 12
Les membres sont différenciés deux par deux, surtout chez les espèces supérieures, ce qui constitue encore un pairage : deux membres avant, deux membres arrière Au point de vue anatomique comme au point de vue fonctionnel, un bras ressemble plus à l'autre bras qu'à une jambe; dans la famille humaine, on ne marche à quatre pattes que dans le bas âge. Il y a des degrés dans le pairage selon les espèces, ainsi l'écureuil saisit les aliments avec ses membres antérieurs, ce dont un cheval ou une vache serait bien incapable.
L'analogie est mathématique entre l'inerte et le vivant de certaines catégories : quadrature avec quadruplicité, pairage dans les deux cas.
On imagine un zoo dans les 30 cases du quart d'ellipse, homme, femme, enfant et hominidés dans certaines cases à pairage vigoureux, le reste de l'arche de Noë ou de la grande salle du Muséum dans les autres cases.
Dans le but de formaliser cette analogie, on pourrait peut-être recourir aux fonctions inventées par Langlet, je crois, décrivant mathématiquement les formes du règne animal. Ces fonctions avaient été présentées au cours d'un congrès de la Société internatioale de biomathématique vers 1990.
En prenant plus plus au sérieux l'analogie des 30 cases, on pourrait mettre à l'essai une classification des quadrupèdes en 30 catégories zoologiques.
30