QbBlocs2005ACFAScompl
Proposition de communication
ACFAS, congrès 2005, UQAC
204 Chimie physique, inorganique et de surface, 515 Pédagogie universitaire
Par affiche
Système du Québécium. Un jeu de blocs qui enseigne la classification elliptique des éléments. Précession de Larmor et pairage des périodes
Pierre Demers, Québécium International.
Problématique. La classification traditionnelle de Mendeleev a de nombreux défauts demandant remède : cases vides ou en surplus, pairage des périodes inexpliqué, périodes inégales, absence de symétrie, correspondance inexistante avec lesétats de l'hydrogène. Méthodologie. Le système du Québécium aboutit à un tableau elliptique des éléments de symétrie 4 avec correspondance exacte avec les états excités de l'hydrogène. Résultats. Notre jeu, avec ses 152 blocs, simplifie l'apprentissage de la classification devenue rationnelle. Il permet de bâtir la classification nouvelle sans les défauts mentionnés. Il explique sans faute les correspondances avec les états de l'hydrogène : 8 périodes bidimensionnelles égales angulairement, terminées uniformément par un élément s+ qui est un gaz rare dans la 1re. Il explique le pairage des périodes par la considération des cônes de la précession de Larmor des spins des électrons associés 4 par 4. "La nouvelle classification des éléments" Éd. PUM 2004 ISBN 2-9802454-7-X et "Le tableau elliptique des éléments" Éd. PUM 2004 ISBN 2-9802454-8-8 par Pierre Demers. www. quebecium.qc.ca.html
COMPLÉMENTS À JEU DE BLOCS 2005
Tableau de Mendeleev.
On le trouve partout, inutile de le montrer ici.
Tableau elliptique.
Voir à la fin.

Fig. 1. Bloc avec gorge.
Blocs
Ce sont des blocs cubiques en bois d'arête 7/8" ou 22 mm. Fig. 1.
32 pour les états de l'hydrogène de H1 au repos à H32 état excité.
120 pour les éléments de z1 pour l'élément Hydrogène à z120 pour l'élément Ubn.
Ils ont une gorge périphérique permettant de les associer jointivement face à face par un élastique 2 par 2 ou davantage : 3 par 3, 5 par 5 ou 7 par 7. Chaque telle association forme un barreau. Deux blocs étant associés de la sorte côte à côte, l'un étant tenu fixe, l'autre peut prendre les positions N, O, S, E au choix sans cesser d'être d'aplomb. Semblablement, trois blocs ou davantage étant associés consécutivement, l'ensemble peut tracer une droite ou une ou plusieurs équerres, les blocs individuels restant d'aplomb.
Si nous avons affaire à deux blocs seulement, leur association en diagonale selon les lignes NO, SE ou SO, NE présentera de l'intérêt.
Correspondance entre les blocs H et les blocs z.
On aligne verticalement la série des 32 blocs H symbolisant les 32 états H choisis de niveaux successifs afin de réaliser les caractères n, l que représentent les atomes au repos.
Devant chaque bloc H, on aligne horizontalement les blocs z symbolisant les éléments. Selon le cas, l'alignement comporte 2, 3, 5 ou 7 blocs z, comme suit, selon le caractère spectroscopique du bloc H. Sur une ligne horizontale, se conservent les nombres quantiques n et l. Pour l différent de zéro, le nombre quantique s se conserve.
Devant un bloc Hs, 2 blocs z, l'un de spin -, l'autre de spin +.
Devant un bloc Hp, 3 blocs z, ayant les valeurs consécutives m = -1, 0 et +1.
Devant un bloc Hd, 5 blocs z, ayant les valeurs consécutives m = -2, -1, 0, +1 et +2.
Devant un bloc Hf, 7 blocs z, ayant les valeurs consécutives m = -3, -2, -1, 0, +1, +2 et +3.
Ces prescriptions découlent du principe de Pauli pour un bloc Hs et du principe de Zeeman pour les blocs Hp, Hd et Hf.
On trouve alors effectivement dans les alignements z les caractères déterminants des 120 éléments; mais ils ne sont pas dans l'ordre connu. Tableau 1.
Tableau 1. Les données sur l'atome d'hydrogène
.Au moins deux états z correspondent à chaque état H.
Effet Pauli : deux.
Effet Zeeman : trois, cinq ou sept.
États H
......……… ……...États zH1
...1s.....-1s0 +1s0........................ .......…................< FONT FACE="Palatino" SIZE=2>z1 z2 H HeH2...-2p...-2p-1 -2p0 -2p1.......................& #133;....…........z5 z6 z7 B C N
H3
….2s....-2s0 +2s0........................ ..........................z3 z4 Li BeH4
...+2p...+2p-1 +2p0 +2p1........................ .............z8 z9 z10 O F NeH5
...-3p...-3p-1 -3p0 -3p1........................ .....….......z13 z14 z15 Al Si PH6
....3sé..-3s0 +3s0........................ .........................z11 z12 Na MgH7
....-3d...-3d-2 -3d-1 -3d0 -3d1 -3d2..................… ..z21 z22 z23 z24 z25 Sc Ti V Cr MnH8
....+3p...+3p-1 +3p0 +3p1........................ ............z16 z17 z18 S Cl AH9
....+3d...+3d-2 +3d-1 +3d0 +3d1 +3d2...................z26 z27 z28 z29 z30 Fe Co Ni Cu ZnH10
..-4p...-4p-1 -4p0 -4p1........................ ..............z31 z32 z33 Ga Ge AsH11
...4s....-4s0 +4s0........................ ........................z19 z20 K CaH12
...-4d..-4d-2 -4d-1 -4d0 -4d1 -4d2.......é.….. .......z39 z40 z41 z42 z43 Y Zr Nb Mo TcH13
...+4p..+4p-1 +4p0 +4p1........................ ...........z34 z35 z36 Se Br KrH14
....-4f...-4f-3 -4f-2 -4f-1 -4f0 -4f1 -4f2 -4f3.....…..< FONT FACE="Palatino" SIZE=2>z57 z58 z59 z60 z61 z62 z63 La Ce Pr Nd Pm Sm EuH15
...+4d..+4d-2 +4d-1 +4d0 +4d1 +4d2................. z44 z45 z46 z47 z48 Ru Rh Pd Ag CdH16
...+4f..+4f-3 +4f-2 +4f-1 +4f0 +4f1 +4f2 +4f3....z64 z65 z66 z67 z68 z69 z70 Gd Tb Dy Ho Er Tm YbH17
....-5p...-5p-1 -5p0 -5p1........................ .............z49 z50 z51 In Sn SbH18
....5s....-5s0 +5s0........................ ......................z37 z38 Rb SrH19
...+5p..+5p-1 +5p0 +5p1........................ ..........z52 z53 z54 Te I XeH20
...-5d...-5d-2 -5d-1 -5d0 -5d1 -5d2....................z71 z72 z73 z74 z75 Lu Hf Ta W ReH21
....+5d...+5d-2 +5d-1 +5d0 +5d1 +5d2...............< FONT FACE="Palatino" SIZE=2>z76 z77 z78 z79 z80 Os Ir Pt Au HgH22
...-5f....-5f-3 -5f-2 -5f-1 -5f0 -5f1 -5f2 -5f3.......z89 z90 z91 z92 z93 z94 z95 Ac Th Pa U Np Pu AmH23
...+5f...+5f-3 +5f-2 +5f-1 +5f0 +5f1 +5f2 +5f3...z96 z97 z98 z99 z100 z101 z102 Cm Bk Cf Es Fm Md NoH24
...-6p...-6p-1 -6p0 -6p1........................ ...........z81 z82 z83 Tl Pb BiH25
...6s…..-6s0 +6s0........................ .....................z55 z56 Cs BaH26
..+6p...+6p-1 +6p0 +6p1........................ ..........z84 z85 z86 Po At RnH27
...-6d..-6d-2 -6d-1 -6d0 -6d1 -6d2...............…... z103 z104 z105 z106 z107 Lr Rf Ra Sg BhH28
...+6d..+6d-2 +6d-1 +6d0 +6d1 +6d2................. z108 z109 z110 z111 z112 Hs Mt Ds Uuu UubH29
...-7p..-7p-1 -7p0 -7p1........................ .............z113 z114 z115 Uut Uuq UupH30
...7s....-7s0 +7s0........................ ......................z87 z88 Fr RaH31
...+7p..+7p-1 +7p0 +7p1........................ ..........z116 z117 z118 Uuh Uus QbH32
...8s....-8s0 +8s0........................ ......................z119 z120 Uue UbuSource des données : http://physics.nist.gov/cgi-bin/AtData/ display.ksh?XXE0qHqIXXT2XXI
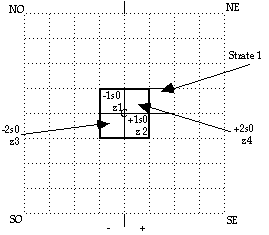
Fig. 2. Strate 1. La strate 1 est définie par le placement de -1s0 et +1s0 et ne peut être complétée que par -2s0 et +2s0. Spin - à l'ouest, spin + à l'est.
Mise en ordre des 120 éléments z.
Première strate.
Nous posons un principe de cohésion. Un barreau est insécable, les fils de caoutchouc étant là pour le rappeler.
Il nous faut en outre le principe de quadrature, qui se définira à mesure de nos démarches et qui repose sur le nombre 4. Celui-ci à son tour demande l'intervention répétée d'une figuration bidimensionnelle, en définitive, nous devons raisonner dans 3 dimensions. Nous nous donnons en conséquence une première grille de carreaux avec origine marquée. Il nous en faudra 3 autres, empruntées au jeu de l'échec avec son échiquier de 64 cases. Nous remplirons les cases avec économie d'encombrement et recherche de symétries. Fig. 2.
Commençons. Dans une grille vide, nous plaçons z1 dans une case située au NO de l'origine. Puis continuons : par souci de symétrie, z2 sera placé en regard de z1 symétriquement par rapport à l'origine dans la case SE disponible. Le lien de caoutchouc du barreau z1 z2 est diagonal.
Les spins ont chacun leur demi-espace, - à l'ouest, + à l'est.
Pour continuer, deux cases se font remarquer, SO et NE. Les remplir complèteraient un carré, figure symétrique à 2 dimensions.
Suivants au Tableau 1 sont les éléments z5, z6 et z7 formant un barreau insécable et 2 cases ne logent pas 3 éléments. De plus ils sont tous de spin - et mieux vaudrait dire qu'on ne peut loger 3 éléments dans une case.
Symétrie et élégance s'unissent pour recommander qu'on emplisse les 2 cases autrement, et les éléments de la ligne suivante z3 et z4 s'offrent, fournissant un barreau diagonal complétant l'occupation du carré, z3 spin - à l'ouest, z7 spin + à l'est.
De la sorte, toutes les cases occupées sont s et nous en avons 4.
Ces toutes premières opérations ont mis en oeuvre un peu du principe de quadrature, c'est un sous-principe : l'amorce du remplisage d'une grille définit le carré de remplissage de la grille bidimenionnelle. Ce carré doit être rempli en priorité. La suite du remplissage réclamera un espace bidimensionnel nouveau, c'est-à-dire d'amorcer une nouvelle grille. Une grille bidimensionnelle remplie est une strate. Une nouvelle grille remplie sera une autre strate.
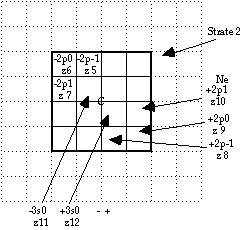
Fig. 3. Installation d'une équerre -2p et apparition de la strate 2. On ajoute l'équerre +2p opposée et on complète les 2 quadrants opposés.
Deuxième strate.
Pour amorcer une 2e strate, nous rencontrons le barreau z5, z6, z7. Disposition éminemment bidimensionnelle, nous en formons une équerre, grâce aux degrés de liberté du barreau. Par choix, elle est orientée NO, z7 en bas à gauche et nous la plaçons dans le quadrant NO de la grille, de spin -, le plus près possible de l'origine. Un carré de remplissage est dès lors défini, 4 cases de côté et nous continuons en occupant le quadrant opposé avec le barreau z8, z9, z10 de spin + formé en une équerre orientée SE, z10 en haut à droite. Ce faisant, nous avons inauguré un autre sous-principe : une équerre de spin - étant placée, la démarche suivante sera de placer symétriquement l'équerre de spin +. Dans la strate 1, il était appliqué automatiquement puisque les blocs spin - et spin + font partie d'un barreau insécable, pourvu que nous considérions chacun de ces blocs comme des équerres d'un bloc (sans bras).
Autre sous-principe que nous allons inaugurer : il faut terminer l'occupation des quadrants opposés avant toute autre démarche, soit, dans le cas présent, les cases NO et SE encore vides. À à cette fin nous trouvons le barreau oblique z11, z12. Et voilà complétée l'occupation des quadrants opposés NO et SE de la strate 2. Fig. 3.
Avant de quitter la strate 2, il nous reste à occuper les quadrants SO et NE. Nous trouvons à cet effet le barreau z13, z14, z15 formé en équerre, z15 en haut, dans le quadrant SO, le barreau z16, z17, z18 formé en équerre avec z18 en bas; puis le barreau oblique z19, z20 avec z20 en haut complète le tout.
De la sorte, les cases de la strate 2 se trouvent organisées géométriquement selon leurs caractères : un coeur de 4 cases s comme dans la strate 1 entourées d'un cadre de 12 cases p.
Les périodes des strates 1 et 2.
Avant de traiter des strates 3 et 4, essayons de comprendre ce qu'il advient des périodes. Dans le système actuel, une période se termine sur un élément +s. De la sorte, la place de l'hélium est fixée et seule la 1re période se termine sur un gaz rare. Les autres se terminent sur un alcalino-terreux. La définition traditionnelle de la période basée sur les propriétés chimiques : "Ce qui se termine sur un gaz rare", est abandonnée au profit des régularités et des symétries basés sur les propriétés électroniques. La chimie des éléments ne se trouve pas altérée pour autant, mais, parvenus à l'élément z20 qui est le calcium, nous sommes en face d'une 1re strate de 2 périodes puis d'une 2e strate de 2 périodes également. Les deux 1res périodes, dans la strate 1, ont chacune 2 éléments, les deux périodes de la strate 2, 8 éléments.
Troisième strate.
Pour amorcer une 3e strate, nous rencontrons le barreau z21...z25 composé de cases d. Nous le formons en équerre symétrique orientée NO, z25 en bas à gauche. Cette fois, nous devons spécifier que l'équerre doit être symétrique, condition réalisée automatiquement sur les barreaux de 3 ou d'une case. Notons que les barreaux s de 2 cases ne se prêtent pas à la formation en une équerre unique. Ils se prêtent par contre à la formation en 2 équerres symétriques (sans bras).
Le barreau z21...z25 étant placé, se trouve défini un carré de remplissage ayant 6 cases de côté.
La suite des opérations ressemble à celles de la 2e strate, sauf une étape supplémentaire pour chaque paire de quadrants, étape que nous avons commencé de décrire : la formation d'un cadre de 20 cases d.
De la sorte, les cases de la strate 3 se trouvent organisées géométriquement selon leurs caractères : un coeur de 4 cases s comme dans les strates 1 et 2, entourées d'un cadre de 12 cases p comme dans la strate 2 et d'un 2e cadre de 20 cases d.
Quatrième strate.
Pour amorcer une 4e strate, nous rencontrons le barreau z57...z63 composé de cases f.
Ce barreau étant placé, se trouve défini un carré de remplissage ayant 8 cases de côté.
La suite des opérations ressemble à celles de la 3e strate, sauf une étape supplémentaire pour chaque paire de quadrants, étape que nous avons commencé de décrire : la formation d'un cadre de 28 cases f.
De la sorte, les cases de la strate 4 se trouvent organisées géométriquement selon leur caractères : un coeur de 4 cases s comme dans les strates 1, 2 et 3, entourées d'un cadre de 12 cases p comme dans les strate 2 et 3, d'un 2e cadre de 20 cases d comme dans la strate 3, et d'un 3e cadre f de 28 cases.
Analyse.
La strate de numéro N commence par un bloc de nombre quantique principal n égal à N.
n croît de la périphérie vers le centre de chaque quadrant.
Quel contraste!Les
dernières lignes du Tableau 1
contiennent, dans la colonne de gauche,
les électrons les plus facilement
extraits de l'atome d'hydrogène
puisqu'ils proviennent des états
les plus fortement excités de cet
atome. Or ces mêmes lignes, dans
les colonnes de droite, renferment les
atomes dont les électrons sont
les plus difficilement extraits, exemple
l'uranium dont l'électron -1s0 a
un potentiel d'extraction de 116000
volts. Il est situé à
-116000 e.v. de l'ionisation et ne se
manifeste qu'en excitation donnant des
rayons-X. Cet atome provient de H22,
situé à -0,85 e.v. de
l'ionisation. La différence
provient évidemment de la charge
du noyau, qui vaut l'unité pour
H22 et 92 pour z92.
Vue d'ensemble. Les 4 strates
étant placées
côte-à-côte
s'inscrivent dans une demi-ellipse de
demi grand-axe voisin de 20 et de demi
petit-axe voisin de 4, l'unité
étant l'arête d'une bloc.
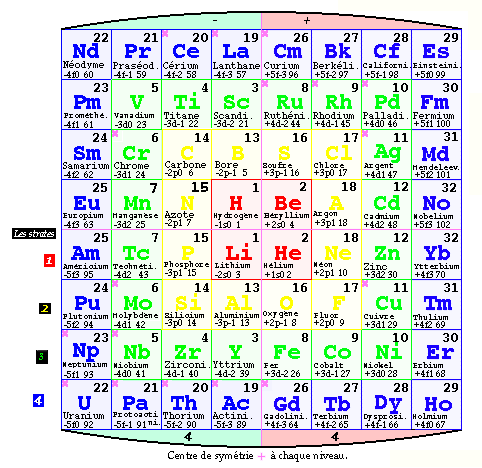
Fig. 4. Tableau elliptique des
éléments. Dans la figure
5, les cubes de la figure 4 ont
été manipulés par
des translations de façon
à réunir les
éléments de chaque strate
selon le signe du spin. Le
résultat s'inscrit dans une
ellipse de demi grand-axe 10,33 et de
demi petit-axe 4,33, l'unité
étant l'arête d'un
bloc.
Fig. 6. Les 4 strates
superposées, le tableau
elliptique devenu tridimensionnel, vue
en projection plane. Groupes et
symétries d'ordre
4. Précession de Larmor du
spin de l'électron et pairage des
périodes. Groupes. Dans une
strate, il existe un groupe de
symétrie 4 pour chaque cadre
présent, y compris le coeur, les
groupes ayant chacun l'une des valeurs
de l : f, d, p ou s. Soit 9 groupes au
total. Dans le tableau elliptique
d'ensemble devenu tridimensionnel par
superposition des cubes des 4 strates,
on reconnaît 4 groupes de
symétrie, un pour chaque valeur
de l : f, d, p ou s. Tétrades.
Dans ce tableau, tous les
éléments appartiennent
à une tétrade. Chaque
tétrade groupe, à
l'intérieur d'une strate, 4
éléments ayant mêmes
valeurs de l et m. Le tableau contient
30 tétrades. Leur existence
explique le pairage des périodes
: une période impaire
étant apparue, une 2e semblable
suivra dans la même strate avec le
même modèle avant qu'un
autre modèle apparaisse. Il
s'exerce une nécessité de
saturer chaque tétrade
amorcée et de ne pas
dépasser cette saturation. Remarque.
L'omniprésence du nombre 4
reflète évidemment une
propriété numérique
importante pour expliquer et comprendre
l'organisation des atomes. On peut
croire qu'elle est reliée
à la figure
géométrique 3D la plus
élémentaire qu'est le
tétraèdre et à
l'assemblage de 4 boules qui le
réalise. En l'absence du spin
de l'électron qui peut prendre
deux valeurs, - et + pour la même
orbitale, les éléments
seraient moitié moins nombreux.
Pauli, en inventant le spin et ses deux
valeurs, a résolu une
énigme. Il faudrait inventer
quelque chose d'analogue pour expliquer
cette autre énigme : les
tétrades qui sont un doublage
d'orbitales, phénomène
équivalent au pairage des
périodes. Si nous cherchons une
variable qui serait associée
à ce pairage, il est
indiqué de choisir le spin de
l'électron plutôt que son
moment cinétique l, puisque ledit
pairage se manifeste dès la 2e
période alors que l = 0 pour les
4 éléments en cause et
pour chaque tétrade s où l
= 0. Cela dans le tableau elliptique. Mais
le pairage s'observe tout autant dans le
tableau de Mendeleev au-delà de
sa période 2. Or le spin, en
présence d'un champ
magnétique, exécute un
mouvement de précession
décrivant un cône d'angle
arc cos 1/racine carrée de 3 =
54,7356 degrés, d'ouverture
109,4712 degrés. C'est la
précession de Larmor. Réf. Gilles
Karcher, Florent ARGOUGES, Alain GUELAT
et Jean D'ESTRESSE,
http://www.ese-metz.fr/metz/eleves/
themes/imagerie/irm_theorie.html Angle thêta.
http://cism.univ-lyon1.fr/dominic/
CoursRMN/chapitre1/bases_physico_texte.
html La
fréquence de cette
précession dépend du champ
magnétique orienteur. La RMN
résonance magnétique
nucléaire met à profit la
précession des noyaux et a des
usages médicaux : IRM imagerie
par résonance magnétique.
Mais ici, il s'agit de la
précession de
l'électron. Il est donc permis
d'imaginer que 4 tels cônes
électroniques s'associent avec un
effet de saturation, en remplissant
l'espace angulaire de 4 pi
stéradians d'ouverture, lors du
doublage d'orbitales réalisant
chaque tétrade. Quatre
cônes d'ouverture 109,4712
degrés placés côte
à côte, de même
sommet, paraissent saturer exactement la
sphère des angles solides, aussi
bien que peuvent le faire des cercles
égaux adjacents d'ouverture
109,4712 degrés. On ne peut pas
en loger davantage, il reste des espaces
vides, aussi bien qu'il en reste dans un
cadre carré plein de boules
égales. Un cône occupe
0,845 pi stéradian. Des questions se
posent. L'assemblage pour une
tétrade ne peut être que de
symétrie 4 donc
tétraédrique. Dès
lors, la disjonction entre spin - et +
demanderait révision puisque les
4 spins d'une tétrade
complète ne peuvent être
collinéaires. Il faut imaginer 4
orientations selon les normales aux
faces d'un tétraèdre : a
et c sont -, b et d sont +. Fig. 7. Il reste aussi à comprendre
l'organisation spatiale de plus d'un tel
tétraèdre. La
considération de ces
tétraèdres donnerait un
fondement pour proposer un modèle
des nuages de probabilités de
présence des électrons
autres que celui de valence dans les
atomes pluriatomiques.-L'analyse RME des
éléments pourrait rendre
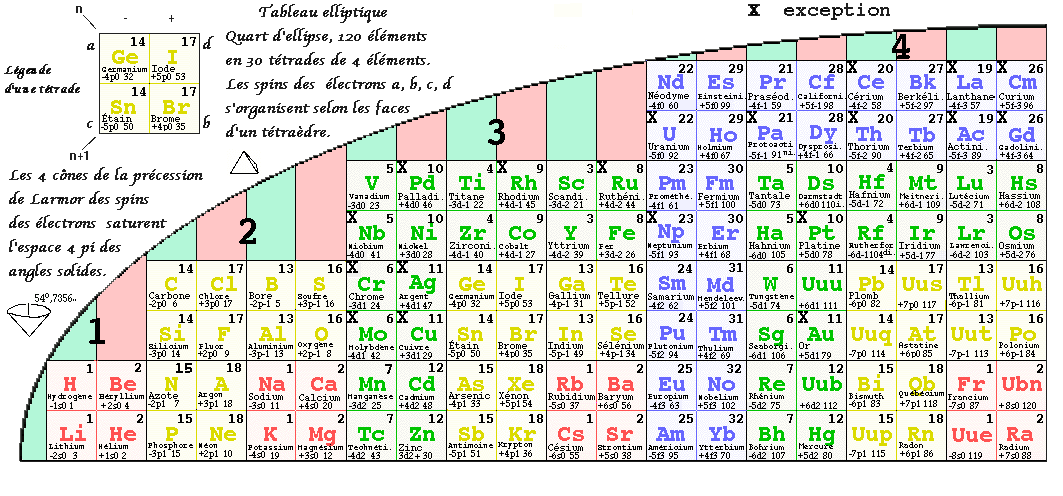
service. Fig. 7. Tableau
elliptique. Quart d'ellipse, les
éléments réunis par
tétrade. Noter les spins a et c
qui sont -, b et d, qui sont +.
L'énigme
du doublage des périodes semble
donc en voie d'être
résolue.
Fig. 8.
Assemblage de 4 cônes de papier
d'ouverture 109,4712 degrés, les
sommets se rejoignant. Assemblage
tétraédrique. - Un
cône s'applique sur une face d'un
tétraèdre par le jeu des
angles supplémentaires, l'angle
dièdre du tétraèdre
étant voisin de 70,5288
degrés. Un
tétraèdre placé sur
une table peut recevoir 3 cônes de
la sorte. Fig. 8bis. Une pyramide
de 4 boules, qui présente les
mêmes symétries
tétraédriques qu'un
assemblage de 4 cônes de la figure
précédente. Voyez les figures 8 et 8bis. Une
pyramide de 4 boules présente les
mêmes symétries
tétraédriques qu'un
assemblage de 4 cônes de la figure
précédente. Elle se
prête elle-même à des
assemblages exacts 3D en nombres
indéfinis. Cette
possibilité a été
mise à profit
précédemment pour
présenter un tableau elliptique
3D de 120 boules ayant la forme d'un
tétraèdre. La
présence insistante des
symétries du
tétraèdre dans la
classification des atomes suggère
que cette symétrie est une
donnée essentielle de
l'organisation des électrons
à l'intérieur des atomes
pluriélectroniques. L'angle 109,4712 degrés se trouve
dans le tétraèdre des quatre valences du
carbone et il est une donnée
essentielle pour comprendre la chimie du
carbone et par suite
celle des vivants. Fig.
9. Les 32 blocs H, les 120 blocs z.
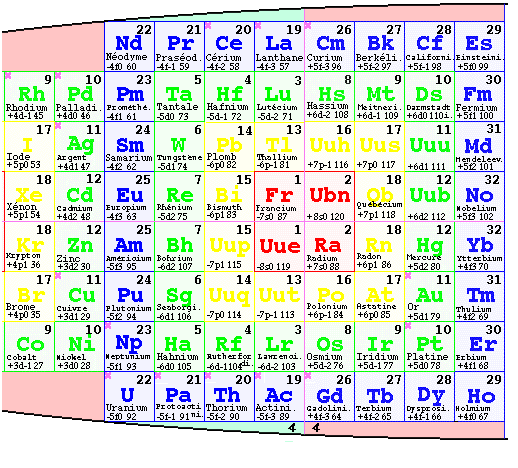 Fig. 4. Vue en projection plane des 4
strates placées côte
à côte. Extrait de
ISBN-2-9802454-8-8
Fig. 4. Vue en projection plane des 4
strates placées côte
à côte. Extrait de
ISBN-2-9802454-8-8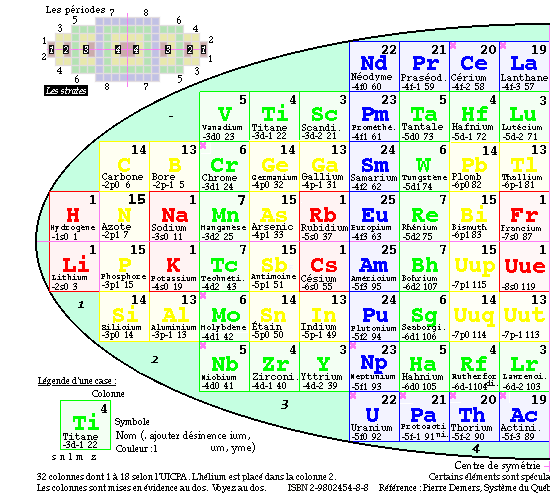
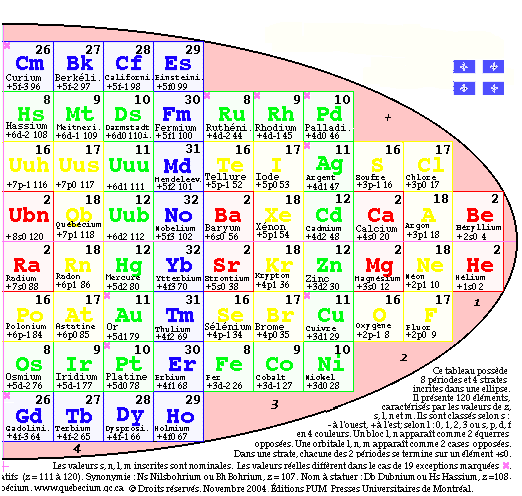 Fig. 5. Tableau elliptique des
éléments. Les cubes de la
figure précédente ont
été manipulés par
des translations de façon
à réunir les
éléments de chaque strate
selon le signe du spin. Extrait de
ISBN-2-9802454-8-8
Fig. 5. Tableau elliptique des
éléments. Les cubes de la
figure précédente ont
été manipulés par
des translations de façon
à réunir les
éléments de chaque strate
selon le signe du spin. Extrait de
ISBN-2-9802454-8-8