QbPlaEvoAtoXI2007bisCOPIE.htm

http://www.er.uqam.ca/nobel/c3410/quebecium.html

Système du Québécium.

Le Platonicisme  

en biologie de l'évolution et en théorie de l'atome

Traduction interdite

Pierre Demers 7XI2007, marges 15 XI 2008

ACP2008QbPlaEvoAtresXI2007 Système du Québécium. Pourquoi avons-nous 56 phalanges et 4 membres? Regard d'un physicien platonicien sur l'évolution biologique. Traduction interdite Pierre Demers Projet de communication à l'ACP 2008 Résumé Je cherche une réponse dans un parallèle entre le squelette humain et le tableau du québécium appliqué aux 120 éléments chimiques. Ce tableau est une grille de 120 cases organisées en 4 strates inégales. Il convient à la classification des atomes pour des raisons quantiques et géométriques. Il définit les nombres magiques 4, 20, 56, 64 et 120. Or le squelette des membres renferme : 4 membres, 20 doigts et orteils, 56 phalanges et 120 os au total. La coïncidence serait-elle purement fortuite? Ou serait-elle la conséquence d'une loi de la nature que le système du québécium exprime et qui conditionne la régulation par les gènes? Cette dernière hypothèse viendrait à l'appui de Owen 1849 et de son platonicisme, de Denton 2002 avec ses reploiements des protéines, de Staune 2007 qui s'oppose au Darwinisme. Financement Entreprise Pierre Demers Voyez http://www.er.uqam.ca/nobel/c3410/QbPlaEvoAtoXI2007bis.htm ACP2008QbPlaEvoAtresXI2007

---

ACFAS2008QbPlaEvoAtresXI2007 Système du Québécium. Un parallèle entre le vivant et l'inerte Traduction interdite Pierre Demers Projet de communication à l'ACFAS 2008 Résumé Sous une méthodologie de recherche de symétrie et d'analogie, je voudrais établir un parallèle entre le squelette humain et le tableau du québécium appliqué aux 120 éléments chimiques. Si on compte les os des 4 membres, on trouve les nombres 4, 20, 56, 64 et 120 (5 doigts et orteils soit le pentadactylisme, pris 4 fois = 20; 56 est le nombre total de phalanges, etc). Or ces nombres sont également les nombres remarquables, "magiques" au sens de la physique, du tableau mentionné. La coïncidence serait-elle purement fortuite? Ou serait-elle la conséquence d'une loi de la nature que le système du québécium exprime et qui conditionne la régulation par les gènes? Cette dernière hypothèse viendrait à l'appui du platonicisme de Owen, de Denton avec ses reploiements des protéines, de Staune qui s'oppose au Darwinisme. Voyez http://www.er.uqam.ca/nobel/c3410/QbPlaEvoAtoXI2007bis.htm ACFAS2008QbPlaEvoAtresXI2007

---

Introduction. Méthodologie.

Je mets ici en regard 2 théories se recommandant de l'illustre Platon l'une en biologie de l'évolution et l'autre en physique de l'atome. Je veux montrer qu'à première vue, elles peuvent paraître totalement distinctes et qu'en fin d'analyse, elles se confondent en une théorie unitaire de la vie et de la matière inerte.

 

Pour les évolutionnistes prédarwiniens, les formes biologiques découlaient d'un modèle platonicien de la nature. Ainsi Owen 1849 8 parlait d'une cosmogonie platonicienne. Quant au platonicisme en physique de l'atome, je propose cette acception nouvelle. du mot pour l'usage que je fais de certains solides dont 3 de Platon, dans l'application du système du québécium à la théorie de l'atome. Le système du québécium a autant sinon plus de relations évidentes avec la géométrie de Platon, que la biologie de l'évolution

 

Ma méthode en est une de recherche de symétries et d'analyse.

 

Remerciements.

Grand merci au prof. Aubert Daigneault qui m'a rendu un signalé service : il m'a fait connaître les travaux de Denton 2002 9 sur les reploiements des protéines et ceux de Staune 2007 11, qui m'ont ouvert le chemin d'une documentation immense sur l'évolution que j'ignorais. On s'instruit ou on périt!

 

Le platonicisme 1. En biologie de l'évolution.

Voici un texte de Denton et Marshall 2001 5 trad. Staune, définissant ce 1er platonicisme.

Avant Darwin, la plupart des biologistes adhéraient à un modèle platonicien de la nature. Cela impliquait que le monde biologique consistait en un ensemble fini de formes naturelles essentiellement immuables qui, à l'instar des formes inorganiques comme les atomes ou les cristaux, faisaient partie intégrante de l'ordre éternel du monde. De même qu'aujourd'hui nous expliquons la structure des atomes et des cristaux par un ensemble de lois physiques ou « de règles de construction », les biologistes pré-darwiniens ont de la même façon cherché à rendre compte de l'origine des formes biologiques en ayant recours à un ensemble de lois physiques génératrices souvent appelées « lois des formes ».

 

À la recherche du platonicisme 1.

Les biologistes pré-darwiniens ont surtout exposé leurs convictions et n'ont guère trouvé de preuves à l'appui, comme en témoignent les dernières lignes écrites par Owen dans son livre-clé paru en 1849, On the nature of limbs. (Denton 2002 9, p. 328). Ils professaient que dans l'évolution, la forme précède la fonction.

 

À partir de 1859, les découvertes et les exposés de Darwin ont ensuite dominé les esprits, avec le principe que le besoin de la fonction fait apparaître l'organe et la forme. Jacques Monod, réputé darwinien, a popularisé des idées analogues dans son livre Le hasard et la nécessité

 

Les preuves les plus convaincantes à mon avis sont apparues vers 1970 et ont été présentées avec force par Denton 2001 5. Elles concernent les reploiements des protéines. Ces reploiements conduisent à des formes principalement en hélice et et feuillets. Si ces reploiements se réalisaient au hasard, le nombre de leurs modèles serait immensément plus grand que celui observé, qui est aux environs de 500 ou 1000.

 

Voici à ce sujet un extrait de Staune 2007  11dans sa conclusion.

Que parmi celles-ci, la (voie la) plus prometteuse que l’on retrouve sous des formes différentes chez Conway-Morris, Denton, Fleury, Grassé, est celle d’une évolution par « lois naturelles » dans laquelle les formes possibles des êtres vivants existent en nombre limité et sont inscrites dans les lois de la nature.

 

... Suite plus bas.

 

Le platonicisme 2. En théoriede l'atome.

Pour parler de ce 2e platonicisme, je rappelle d'abord comment le système du québécium permet d'établir un modèle original de tableau, le tableau du québécium. En bref, il est une grille comprenant 120 cases organisées en 4 strates inégales, il manifeste des symétries et met en évidence des nombres magiques. Il affecte par exemple la forme générale d'un quart d'ellipse ou d'une demi-ellipse.. Fig. 1.

 

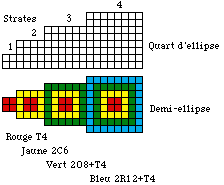
Fig. 1. Tableau du québécium. Dans la forme en quart d'ellipse, 4 cases contigües composent une tétrade d'éléments qu'on a des raisons de rapprocher. Il y a 30 tétrades.- T, C, O, R : tétraèdre, cube, octaèdre, rhombododécaèdre. qbgenerafig1

En me basant sur les propriétés des moments cinétiques à l'intérieur des atomes, j'ai signalé précédemment une relation entre entre l'organisation de la grille du québécium et 4 solides dont 3 de Platon.

 

Je voudrais maintenant signaler que cette relation existe indépendamment des propriétés des moments cinétiques. Voici comment. Elle est basée sur le nombre de faces des solides concernés, voilà le chiffrier correspondant.

De Platon

T4, Tétraèdre régulier, nombre de faces 4

C6, Cube, nombre de faces 6

O8, Octaèdre régulier, nombre de faces 8

Autre

R12, Rhombododécaèdre régulier, nombre de faces 12

 

Voilà comment j'utilise ce chiffrier pour expliquer le nombre de cases de chaque strate. Rouge T4, jaune 2C6, vert 2O8+T4, bleu 2R12+T4. Fig. 1.

 

Pour rouge, un seul chiffre suffit, de même pour jaune. Pour vert, 2 chiffres sont nécessaires, de même pour bleu.

 

La grille du québécium est un assemblage ou une architecture exprimant les propriétés numérisables des formes géométriques de certains solides. 1, 26

 

Recherche du platonicisme 2.

Le tableau du québécium est adapté à l'affichage des éléments chimiques, s'accordant avec ce qu'on connaît de la théorie quantique de l'atome. Fig. 2. 1

 

 

Fig. 2. Tableau des 120 éléments chimiques. Le tableau du québécium s'applique aux éléments chimiques du traditionnel tableau de Mendeleev. Il  met alors en évidence principalement une symétrie d'ordre 4 entre ces éléments. QbPlaEvoAtoXI2007bisfig2.gif

J'ai trouvé en 2005-6 que l'analyse des moments cinétiques des atomes conduit à postuler la présence de formes géométriques virtuelles qui les accompagnent. Les formes sont celles de 4 solides dont 3 sont des solides de Platon.

 

Étant donné ces observations, il n'est plus possible d'ignorer ces solides et leur géométrie dans notre conception de la matière inerte et de l'univers, la conception nouvelle étant très différente de la conception originale de Platon avec ses 4 éléments. Les solides de Platon interviennent dans une nouvelle théorie de l'atome encore incomplète, qui mérite elle aussi de s'appeler platonicisme. Ce platonicisme est porteur d'une "loi naturelle", faisant partie de "l'ordre éternel", pour emprunter ces grands mots aux naturalistes.

 

Recherche du platonicisme 1 (Suite).

Voilà des observations originales. Le tableau du québécium aurait-il aussi des applications biologiques, en plus de ses applications physiques? La réponse est affirmative.

 

Le code génétique. En effet, au niveau moléculaire, il convient à représenter 84 biomolécules essentielles à la vie, comme je l'ai signalé dès 1995 21. Les biomolécules sont d'ordinaire décrites en 2 listes : code génétique et acides aminés fondamentaux. Le tableau du québécium permet de rassembler ces 2 listes de façon fonctionnelle. Fig. 3. 4

 

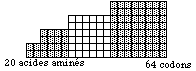
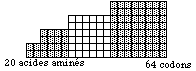
Fig. 3. Tableau des 84 biomolécules.

L'existence de ccs 84 biomolécules et leur organisation mutuelle, est une conséquence de lois naturelles, et le système du québécium en manifeste les aspects apparaissant dans cette figure. En confondant les lois et leur manifestation, le système du québécium "impose" l'existence de ccs biomolécules. QbPlaEvoAtoXI2007bisfig3.gif

 

Le squelette. Au niveau de l'observation courante maintenant, je signale d'autres applications biologiques originales du tableau du québécium, celles-là macroscopiques, touchant le squelette humain (et celui des êtres vivants supérieurs). L'observation en est accessible à quiconque, au besoin au moyen d'une glace. Partiellement dans 3.

 

Les 4 membres. Leur décompte peut se figurer dans la 1re strate de 4 cases. Fig. 4.

 

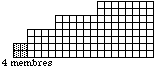
Fig. 4. Les 4 membres, 2 bras, 2 .jambes. QbPlaEvoAtoXI2007bisfig4.gif

Les 5 doigts. C'est l'affirmation du pentadactylisme. Chaque membre se termine par 5 doigts ou orteils. Voilà bien l'énigme, qui consternait Owen cherchant à l'expliquer en 1849 9. Les bébés humains naissent les uns après les autres ayant 5 doigts à chaque main et 5 orteils à chaque pied que les parents comptent joyeusement. Mais considérons le pentadactylisme augmenté d'un facteur 4 puisqu'il accompagne invariablement une symétrie 4 des membres, soit le tétramembrisme (ou la tétrapodie) et parlons plutôt  d'icosidactylisme. Les 20 doigts et orteils trouvent leur place dans un tableau du québécium où ils occupent 4 tétrades des strates 1 et 2. Fig. 5.

 

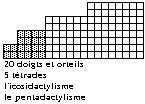
Fig. 5. Le pentadactylisme. L'icosidactyisme des 20 doigts et orteils.QbPlaEvoAtoXI2007bisfig5.gif

Dénombrons maintenant les phalanges. Nous en trouvons 14 dans chaque membre, soit 56 au total, ce qui occupe 14 tétrades des strates 1, 2 et 3. Fig. 6.

 

Fig. 6. Les 56 phalanges des membres.QbPlaEvoAtoXI2007bisfig6.gif

Essayons de compter les os des membres. Villemin a fait cet exercice et trouve 30 os constants dans chaque membre, soit 120 au total. Cela emplit exactement les strates 1, 2, 3 et 4 du tableau. Fig. 7.

 

 

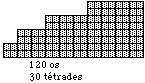
Fig. 7. Tableau des 120 os des membres.QbPlaEvoAtoXI2007bisfig7.gif

L'existence de ces 120 os et leur organisation mutuelle, est une conséquence de lois naturelles, et le système du québécium en manifeste les aspects apparaissant dans cette figure. En confondant les lois et leur manifestation, le système du québécium "impose" l'existence de ces 120 os et leur organisation ou il en est la raison d'être.

 

Des observations à la portée de tous confirment donc ce que le laborieux examen des reploiements moléculaires nous apprend.

 

Essayons d'employer le langage de Staune et de Denton : les «règles de construction » des atomes étant le platonicisme des atomes; et les lois physiques génératrices souvent appelées « lois des formes » étant le platonicisme de la biologie, nous dirons que ces règles, lois et platonicismes se ramènent à une méthodologie unique, qui est celle des symétries et des nombres magiques contenus dans la grille et le système du québécium.

 

Tétramembrisme et tétradisme de l'être humain.

Le fait de 4 membres ne se limite pas au squelette. Il faudrait examiner le système musculaire et le système nerveux des membres et remonter jusqu'au cerveau. Certaines représentations de l'homunculus cérébral accordent une importance primordiale à la bouche, puis aux mains et aux pieds. La grille du québécium, les nombres magiques 4, 20, 56, 64 et 120 pourraient servir de guides pour trouver des relations nouvelles.

 

Le système du québécium système unitaire.

Le système du québécium apporte un principe de symétrie ou d'unité entre matière inerte et vivante, en accord  avec la définition de la vie par Vincent et Nibart 2002. Pour eux, la vie est un 5e état de la matière à côté des états gaz, liquide, solide et plasma.

 

Ces résultats ont une portée évolutionniste et favorisent les vues pro-Geoffroy Saint-Hilaire, pro Owen, anti-Darwin et anti-Monod de Denton et de Staune 2007 11. Ils confirment une proposition de ce dernier : "les formes possibles des êtres vivants existent en nombre limité et sont inscrites dans les lois de la nature".

 

Ces énoncés paraissent indéniabes. Mais comment se fait-il qu'il en soit ainsi? Il faut croire que des mécanismes différents, les uns dans les atomes et les autres dans les organismes vivants, convergent vers des résultats systémiquement comparables. Essayons de comprendre quels peuvent être les mécanismes mis en jeu.

 

Les mécanismes.

Matière inerte. La théorie quantique est fort satisfaisante pour l'atome d'hydrogène mais sa transposition aux atomes  pluriélectroniques n'explique que partiellement le tableau des éléments, entre autres le fait de strates contenant régulièrement 2 périodes; or ce fait est primordial pour expliquer l'existence des 30 tétrades des éléments.

 

Tenons compte maintenant des aspects platoniciens, c'est-à-dire considèrons en outre les affinités géométriques. Elles expliquent le fait de strates contenant régulièrement 2 périodes. L'ordonnance des sous-couches complètes des éléments s et p dans les 4 strates s'explique sans faute par des correspondances avec les 2 solides de Platon que sont le tétraèdre et le cube. Quant à l'ordonnance des demi-sous-couches complètes des éléments d et f dans les strates 3 et 4, elle s'explique sans faute elle aussi par des correspondances avec le tétraèdre et l'octaèdre, qui sont des solides de Platon, et avec le rhombododécaèdre régulier. Le cas des éléments qui renferment des demi-sous-couches incomplètes ne nous importe pas.

 

Les solides interviennent ainsi pour les sous-couches 1.

s, tétraèdre

p, cube

d, octaèdre et tétraèdre

f, rhombododécaèdre régulier et tétraèdre

 

Nous pouvons spéculer : l'architecture du système du québécium paraît trop bien fondée, dans le cas de la matière inerte, pour qu'elle ne s'applique qu'à elle seule.

 

Matière vivante. Les biomolécules. Je constate : les 64 codons et les 20 acides aminés occupent correctement les strates 4, 2 et 1 du système du québécum.

 

Il faudrait découvrir un mécanisme plausible qui aurait déterminé les structures des molécules en cause afin de s'ajuster à cette nécessité 4.

 

Le mécanisme existe pour ce qui est de la strate 4, si on admet 1) qu'il existe 4 bases azotées T, A, C, G intervenant par 4 paires orientées TA, AT, CG, GC dans l'ADN, et 2) qu'elles forment des triplets ordonnés constituant les codons. Il est inévitable alors que les codons soient au nombre de 64 et remplissent les 64 cases d'une strate 4. Mais pourquoi les propositions 1) et 2) sont-elles vraies?

 

Quant à la proposition 1), nous avons une sorte de raison : les 4 paires occupent une strate 1 et réalisent le nombre magique 4. Fig. 8.

 

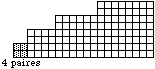
Fig. 8. Les 4 paires orientées TA, AT, CG, GC des 4 bases azotées de l' ADN : T, A, C, G. QbPlaEvoAtoXI2007bisfig8.gif

Quant à la proposition 2), voici peut-être le commencement d'une explication. On sait que l'ADN, qui est une chaîne en hélice double, donne naissance, au cours de la transcription, à une chaîne simple d'un brin appelée ARNm acide ribonuccléique messager. Or le nombre 3 intervient dans la structure de l'ARNm, car il est formée d'une succession de triplets, chaque triplet étant une succession de 3 bases azotées parmi les 4 que voilà : U, A, C, G. Cela se rapporte à la proposition 2), puisque 64 = 4 élevé à la puissance 3.

 

 - Je n'aperçois aucun mécanisme pour les strates 1 et 2.

 

Matière vivante. Les membres.

 

J'ai essayé de comprendre les données sur les symétries du développement et je soumets ce qui suit avec réserve et j'espère qu'un expert voudra me corriger. Le vocabulaire étendu qui est nécessaire et les nombreuses métamorphoses des parties constituantes, déroutent l'apprenti passim1-25.

 

L'être humain manifeste 3 axes trirectangles.

A-P, ou tête-pieds (antéro-postérieur chez les quadrupèdes);

D-V dorso-ventral, derrière-devant, également appelé axe aboral-oral, A-O;

D-G des côtés droit et gauche, axe droite-gauche. Fig. 9.

 

 

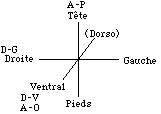
Fig. 9. Les trois axes trirectangles de l'être humain. L'axe droite-gauche est de symétrie miroir. QbPlaEvoAtoXI2007bisfig9.gif

Il y a une polarité créée dans l'ovule dès la pénétration du spermatozoïde. Le futur globule polaire se développe du côté femelle. C'est le pôle animal, son opposé étant le pôle végétal ou végétatif. C'est l'axe animal-végétatif. Ceci pour l'ovule unicellulaire au jour 0. Au jour 1, on trouve 2 cellules accolées par un plan contenant cet axe. Au jour 3, on trouve 4 cellules disposées en tétraèdre. Cependant, ce tétraèdre n'est pas exactement symétrique, car la 2e division ne s'est pas faite simultanément pour les 2 1res cellules. En termes techniques : "la première division se fait selon un plan méridional passant par les pôles du zygote. Ensuite, un des deux blastomères résultants se divise également selon un plan méridional. L'autre blastomère, par contre, se divise selon un plan équatorial." 19. Entre les jours 1 et 2, on trouve donc 3  blastomères et je crois comprendre qu'à ce moment se déterminent, dans le plan équatorial, les 2 axes définitifs A-P et D-G, l'axe animal-végétatif devenant dos-ventre D-V A-O.

 

Au 6e jour, lorsqu'il y a une centaine de ccllules, c'est le stade blastula. L'épiblaste est du côté animal, l'hypoblaste du côté végétatif. La blastula jusqu'alors flottante dans la cavité utérine se nidifie : elle se fixe en pénétrant, pôle animal en premier, dans la muqueuse utérine, vers le 9e jour.

 

Après diverses péripéties, vers le 30e jour, l'embryon a pris une forme cintrée, le dos à l'extérieur. Les 3 axes sont évidents. Fig. 10.

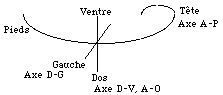
Fig. 10. Trois axes trirectangles chez l'embryon au 30e jour.Qb. PlaEvoAtoXI2007bisfig10.gif

À ce moment, les bourgeons des membres supérieurs apparaissent simultanément droite et gauche. Ceux des membres inférieurs apparaissent simultanément droite et gauche vers le 32e jour. Les mains et les pieds apparaissent, vers le 39e jour, sous la forme de palettes où les doigts sont indistincts comme dans un moufle.

 

Vers le 46e jour, les doigts sont devenus distincts et il en est de même pour les orteils vers le 51e jour. La séparation des doigts et celle des orteils se font par une apoptose ou mort programmée des tissus intermédiaires. L'origine des 56 doigts et orteils : le nombre magique 56, essentiel dans le pentadactylisme et l'icosidactylisme discutés Fig. 4, trouve donc son origine bio-médicale dans cette apoptose limitée. Il serait intéressant de découvir quels sont les gènes ou les portions de gènes spécifiques programmateurs de cette apoptose et de sa limitation.

 

Les mains et les pieds se rapprochent et se touchent, c'est ce qu'on appelle la pronation.

 

Le développement des membres est régulé par des gènes. Les mêmes gènes interviennent en deux étapes distinctes : pour les membres supérieurs puis à nouveau pour les membres inférieurs. Cela expliquerait la similitude des résultats : 30 os dans chacun des membres etc. Réf. gènes homéotiques Hox A1, Sonique Hérisson bleu, Hedge Hog, auteurs Duboule, Kmita etc. Des gènes comparables interviennent pour tous les êtres vivants supérieurs.

 

La vie extraterrestre.

La vie serait possible sur les autres planètes du système solaire, selon les opinions de Denton après Owen et plusieurs autres. Les considérations ci-dessus permettent d'ajouter à ces affirmations. Puisque nous reconnaissons, dans le spectre lumineux d'une étoile lointaine,  les éléments inertes connus, nous sommes maintenant en droit de postuler que là aussi le système du québécium avec sa platonicité s'applique à la matière vivante autant qu'à la matière inerte

 

Que le système du québécium permet là-bas, aussi bien que dans le voisinage de notre soleil, l'existence des mêmes biomolécules essentielles et des formes squelettiques qui nous sont familières. Que non loin de cette étoile peut exister une vie comparable à celle que nous connaissons ici-bas.

 

Questions.

Pourquoi donc le parallèle présenté s'applique-t'il si bien et précisément au squelette des membres humains parmi la plèthore des formes dénombrables de la vie? S'appliquerait-il ailleurs aussi dans l'être humain et ailleurs dans cette plèthore? Voilà un champ d'exploration considérable qui se présente. En réalité, le cas de l'être humain n'est pas tout à fait isolé, tous les êtres vivants supérieurs EVS semblent présenter des dénombrements comparables dans leurs membres, même la baleine et la chauve-souris. Il faudrait voir la mesure de cette comparaison. - Faudrait-il imaginer que l'évolution a attendu l'apparition des EVS avant d'appliquer à la vie une loi de la nature, mise en réserve depuis la confection des atomes inertes des milliards d'années auparavant? - Je souhaiterais faire références aux vues sur l'évolution de feu mon collègue le prof. Jean-Romuald Beaudry, décédé en 2006. Il a laissé, je ne sais pas entre quelles mains exactement, un grand manuscrit inédit dont le titre serait "L'évolution des espèces d'Aristote jusqu'à nos jours". Grâce à l'aide de quelques uns de ses amis, j'espère que ce document précieux sera retrouvé et qu'il deviendra accessible à moi et à tous. - J'ai trouvé beaucup à apprendre dans son livre sur la génétique publié en 1985 27. - Pour comprendre les mécanismes de l'embryologie des membres, il faudra faire référence au travail récent de Lévesque et Roy sur la régénération des tissus de la salamandre axolotl 28. http://nouvelles.umontreal.ca/content/view/687/1/

 

Références.

1. Pierre Demers, Site Qb, http://www.er.uqam.ca/nobel/c3410/quebecium.html

2. Pierre Demers, Chapitre 3 Applications aux biomolécules Emploi des tableaux du Québécium Le code biomoléculaire http://www.lisulf.quebec/QbSyst2e.6.htmll

3. Pierre Demers, http://www.lisulf.quebec/tetradesdossaBIS.html

4. Pierre Demers, http://www.lisulf.quebec/PierreDemersBibl1990-9.html, 859, 860, 870, 874, 876, 889, 1995-1999, http://www.lisulf.quebec/QbSyst2e.6.html, figure 60 etc.

5. Michael Denton et Craig Marshall, Nature, 410, 22 mars 2001, p. 417

http://64.233.167.104/search?q=cache:M5iVsy_EdfMJ:www.staune. fr/spip.php%3Fpage%3Darticle_pdf%26id_article%3D152+staune +revisit%C3%A9es&hl=fr&ct=clnk&cd=1

6. Jean Staune, http://www.staune.fr/.

7. Duboule, Kmita et Tarchini, Les gènes Hox et Hedge Hog, , 2006 http://www.iforum.umontreal.ca/DesNouvellesDe/2006-2007/20061026_IRCMGenesBras.html

Regulatory constraints in the evolution of the tetrapod limb anterior–posterior polarity, http://www.nature.com/nature/journal/v443/n7114/full/nature05247.html

8. Owen, R. 1849, On the Nature of Limbs, Van Voorst; 1866, Anatomy of Vertebrates, Longmans

9. Denton, Marshall, Legge J. Theor. Biol. (2002) 219, 325-342  http://www.idealibrary.com.on,,, doi:10.1006/yjtbi.3128

10. Michael Denton, P. K. Dearden,  S. J. Sowerby, 2003 ,,, www.elsevier.com/locate/biosystems www.sciencedirect.com,,, http://www.sciencedirect.com/science?_ob=ArticleURL& _udi=B6T2K-49KH9XX-2&_user=10&_coverDate=10%2F31%2F2003& _rdoc=1&_fmt=&_orig=search&_sort=d&view=c&_acct =C000050221&_version=1&_urlVersion=0&_userid=10& md5=456812af82655817eb41dc2ad23b096e

11. Staune 2007

http://www.staune.fr/-Les-mecanismes-de-l-evolution-.html

12 Michael Denton, Evolution, une théorie en crise, éditions Flammarion, collection ChampsPoche, 1993, ISBN : 9782080812285;

13. Michael Denton, L'évolution a-t-elle un sens ?, ISBN-10: 2213597480 .éditions Fayard 1997.

14. Gérard Villemin, Répartition des 206 os constants. Membres inférieurs; 60. Membres supérieurs; 60. Crâne; 29. Thorax; 57. http://villemin.gerard.free.fr/Biologie/Squelett.htm

15. Bertrand Boutillier, Pr. Gérard Outrequin, http://www.anatomie-humaine.com/

16. http://mapageweb.umontreal.ca/cabanat/bio2460/gastrulation.html

polarité dorso-ventrale

17. http://www.medisite.fr/medisite/images/public/femmes/grossesse/embryo.swf

18. http://homepage.mac.com/danielbalas/EMBRYO/embdes/embdes1.html#s1

19. http://fr.wikipedia.org/wiki/Embryogen%C3%A8se_humaine#

20. Sardet et al2004, http://www.erudit.org/revue/ms/2004/v20/n4/008115ar.html

21. Pierre Demers, biomolécules, http://www.lisulf.quebec/PierreDemersBibl1990-9.html, 859, 860, 870, 874, 876, 889, 1995-1999

22. A. Senn et al., ch carnegie,  Suisse en français, http://www.embryology.ch/

23. Bonaventure J . Gènes du Développement. Exemple: Développement du squelette chez l'humain. Atlas Genet Cytogenet Oncol Haematol. Septembre 2001 .

URL : http://AtlasGeneticsOncology.org/Educ/GenDevelShortFr.html

24. Furelaud, Gilles, Le gène homéotique Hox A1 chez l'Homme et la souris, http://www.snv.jussieu.fr/vie/dossiers/sequences/hoxa1/hoxa1.htm#haut_pag

réf. Professeur Aristide Lafleur,

25.  http://cvirtuel.cochin.univ

http://cvirtuel.cochin.univ-paris5.fr/Embryologie/AnimEntre/AnimEntre1.html paris5.fr/Embryologie/AnimEntre/AnimEntre1.html

26. Pierre Demers, Genèse géométrique du tableau du québécium, http://www.er.uqam.ca/nobel/c3410/QbGeneraXI2007quater.htm

27. Jean-Romuald Beaudry, Génétique générale, 504pp., Décarie 1985, ISBN2-89137-028-7 http://www.decarieediteur.com/biologiebiologiemedicalemedecine.php3

28. Mathieu Lévesque et Stéphane Roy. Faire repousser un membre amputé. 28XI2007 http://nouvelles.umontreal.ca/content/view/687/1/

Fig. 11. La tradition du géomètre Platon (-427 à -347), était déjà ancienne pour l'architecte Vitruve (-90 à -20); elle s'est continuée depuis la Renaissance. Le présent travail ajoute à cette tradition.

QbPlaEvoAtoXI2007bis

http://www.er.uqam.ca/nobel/c3410/quebecium.html

-30-