QbSansvXI2007bis.htm

Système du Québécium

Solides sans volume

Traduction interdite

Pierre Demers

Résumé ACFASbis

Solides réguliers nouveaux : 4 solides sans volume. Ma méthodologie est de procèder à une translation virtuelle des faces du solide régulier jusqu'au centre de figure; transformant la figure en une collection de cellules ouvertes et le volume enfermé devenant nul. J'envisage les 5 solides de Platon, le rhombododécaèdre régulier et les 5 solides coiffés qui leur sont associés. Le rhombododécaèdre régulier est important dans le système du québécium. Issus de ces 11 solides réguliers à divers titres, j'aperçois la possibilité d'au moins 4 solides sans volume originaux, qui seraient aussi des solides réguliers, dont je montre la réalisation papier : 1 le tétraèdre sans volume, 2 le cube, 3 le rhombododécaèdre et 4 le rhombododécaèdre étoilé sans volume. Ces solides s'ajoutent à ceux de Platon, de Képler et de Poinsot. http://www.lisulf.quebec/ACFAS2008QbSansvXI2007bis.html

 

Méthodologie et résumé.

Je procède par une translation virtuelle des faces du solide jusqu'au centre de figure; à ce moment, le volume enfermé est nul dans le cas le plus simple, celui du cube : les faces opposées se rejoignent 2 à 2 et déterminent 3 plans et 8 cellules qui sont des octants vides. Fig. 2 J'envisage 11 solides normaux : les 5 de Platon, le rhombododécaèdre régulier à cause de son importance dans le système du québécium, et les 5 solides coiffés qui leur sont associés. Le processus valable dans le cas du cube s'applique aussi au tétraèdre régulier, au rhombododécaèdre régulier et au rhombododécaèdre régulier coiffé: voilà 4 solides sans volume originaux. Ils s'ajoutent à ceux de Platon, de Képler et de Poinsot. Le tétraèdre sans volume se distingue parce qu'il est formé de surfaces ayant un seul côté : on pourrait les appeler des surfaces anti-Möbius. Le processus ne s'applique pas à l'octaèdre régulier, au dodécaèdre régulier et à l'icosaèdre régulier. Pour 4 solides coiffés, ma recherche se poursuit.

 

Solides réguliers et leurs dérivés.

Quand on veut obtenir un solide coiffé, on manipule le solide original en agissant sur ses faces, la manipulation consistant en une prolongation des faces sans altération des angles mutuels dièdres qu'elles forment. Cette prolongation des faces est accompagnée d'une prolongation des arêtes segments de droites rencontres des faces. Ces rencontres ne déterminent pas d'angles dièdres de valeurs nouvelles; en revanche, les angles polyèdres à la rencontre de plus de 2 faces prolongées ont des ordres nouveaux, par exemple l'ordre 6 en plus de l'ordre 3, quand on passe du dodécaèdre régulier au petit dodécaèdre étoilé qui en dérive.

 

La manipulation décrite au paragraphe précédent appartiendrait-elle à une catégorie plus générale de manipulations sur un solide qui préserverait le caractère essentiel à l'identification du solide qu'est l'angle dièdre à la rencontre de 2 faces? La catégorie qui apparaît contient alors, outre la prolongation des faces, leur déplacement par translation. Appelons cette catégorie dérivation et disons que dérivation contient prolongement et translation des faces. La catégorie dérivation que je considère exclut les rotations.

 

La dérivation par prolongement conduit aux formes étoilées et s'appelle stellation. Quel est le résultat dérivant de la translation? Sauf contraintes imposées, le résultat est multiple et contient par exemple les parallélipèdes si l'on agit sur un cube. Ainsi, un cube devient une poutre.

 

Procéder à des translations ou à des prolongements des faces : dans les deux cas, les angles dièdres originaux se conservent.

 

Il y a peut-être un lien à établir avec les idées d'Emmy Noëther sur symétries de translation et principes de conservation en physique. Merci à mon fils Thierry qui m'a fait connaître une référence récente à ce propos : Chown, Marcus. "The hypertime trap", New Scientist, vol. 196, no.2625, October 13-19, 2007, pp.36-39.

 

 

Translations.

J'impose des contraintes de la façon que voici. À chaque face je garde ses dimensions et ses angles plans. Je la déplace d'un mouvement rectiligne en amenant son centre au centre de figure du solide donné. Par exemple, le déplacement est synchrone pour toutes les faces, de sorte qu'à chaque instant, le volume enfermé reste homothétique, tout en devenant de plus en plus petit. Finalement, il est nul et réduit à un point.

 

Ce programme s'applique sans problème au cube : les faces opposées sont des carrés qui s'appliquent l'un sur l'autre dans le résultat final et se confondent. Dans le cas du rhombododécaèdre, les faces losanges font de même. Dans le cas du tétraèdre régulier, les faces n'ont pas de vis-à-vis. Au cours du déplacement synchrone, elles enferment à chaque instant jusqu'au dernier, un volume tétraédrique, mais à sa fin, elles sont isolées et n'ont pas de vis-à-vis qu'elles puissent rencontrer et avec lequel elles puissent se confondre.

 

Dans le cas de l'octaèdre, du dodécaèdre et de l'icosaèdre réguliers, j'ai pu croire que le processus serait applicable, puisque les faces viennent 2 par 2 vis-à-vis opposées parallèles et de formes planes semblables. Cependant, il me paraît maintenant sans intérêt parce que les faces opposées ne coïncident pas par une pure translation. La translation seule suffit pous amener à confondre 2 faces vis-à-vis dans un plan unique, mais à ce moment, leurs formes sont décalées. Pour amener en coïncidence leurs formes, il faudrait ajouter une rotation : 2π/6 pour l'octaèdre et l'icosaèdre, 2π/10 pour le dodécaèdre. Or, dans un souci de préservation des symétries choisies, j'exclus les rotations.

 

Afin d'obtenir des figures homothétiques dans le cas de l'octaèdre, du dodécaèdre et de l'icosaèdre réguliers, le processus naturel fait appel aux symétries de ces figures par rapport à un point qui est le centre de figure. La symétrie par rapport à un point et la symétrie par translation que je propose ici ne sont pas nécessairement équivalentes.

 

J'appelle solide régulier sans volume un solide dérivant de l'un des solides réguliers de la liste, après transformation par le processus décrit de pure translation.

 

Jusqu'ici, je réservais le cas des 5 solides coiffés. Pour l'un d'entre eux, la solution m'est apparue récemment : rhombododécaèdre coiffé se prête à produire un solide sans volume. Je réserve encore le cas des 4 autres solides coiffés.

 

Le programme  s'applique donc pour faire apparaître au moins les 3 solides sans volume suivants, qui me paraissent mériter l'appellation de solides réguliers aussi bien que les solides coiffés :

tétraèdre régulier sans volume,

cube sans volume,

rhombododécaèdre régulier sans volume,

le rhombododécaèdre régulier coiffé sans volume.

 

1. Le tétraèdre régulier sans volume.

Quatre triangles ayant intersection deux à deux, qui morcellent chaque face en 9 triangles équilatéraux. Le volume fermé par ces triangles est nul, ils dessinent 14 cellules de 3 sortes ayant toutes un sommet au centre et formées de triangles équilatéres. Les cellules :

 

4 ont une ouverture triangulaire et ont pour faces 3 triangles équilatères;

 

4 ont une ouverture triangulaire et ont pour faces 3 losanges de 2 triangles équilatères;

 

6 ont une ouverture quadrangulaire et ont pour faces 2 triangles équilatères et 2 losanges de 2 triangles équilatères.

 

Les angles dièdres sont 109,471o ou son supplément 70,528o.

 

On remarque la manifestation de symétries 3 et 4, en accord avec les nombres entiers impliqués 2 et 3.

 

Tous les sommets sont simples, d'ordre 1. Ils sont ceux d'une surface de dimension 2 : ce sont des surfaces n'ayant qu'un côté.

 

L'objet obtenu s'inscrit dans un tétraèdre dont le côté vaut les 4/3 de celui du tétraèdre original

 

1bis. Le tétraèdre régulier sans volume 12 a 4 faces, aussi bien que le tétraàdre régulier 1 dont il provient, parce que ce dernier ne possède aucune face parallèle à une autre, quoique le nombre de ses faces soit divisible par 2.

 

1ter. Surface n'ayant qu'une face. Surfaces anti-Möbius. On est confronté à certains exemples de surfaces où l'on peut passer sans discontinuïté d'une face à son opposée, du type Möbius. Elles sont développées dans 3 dimensions et elles ont des portions courbes. La présente analyse nous place devant un cas opposé, où apparaît une surface bidimensionnelle plane limitée n'ayant qu'une face et où, parhypothèse et construction, on n'a aucun moyen de passer à la face opposée. On pourrait l'appeler surface anti-Möbiüs. Non seulement est-il impossible de passer à la face opposée, mais encore celle-ci est inexistante. Elle n'a pas d'existence.

 

Au lieu de parler d'existence, on pourrait parler de visibilité, les 2 concepts  ayant quelque chose en commun : la surface serait visible d'un côté mais non de l'autre. Voici des exemples. Les vitres permettant d'observer sans être vu; la transmission d'images par télévision, le spectateur voyant le programme sans être vu; plus généralement, l'information d'une photo ou d'un portrait qui se transmet de sa source vers l'observateur mais non en sens inverse. Enfin, la flèche du temps fait que l'information se transmet du passé au futur.

 

Il y a une absence de symétrie : un observateur imaginaire qui traverse la surface qu'il voit se trouve perdu, il est incapable de voir la surface qu'il vient de traverser et de retrouver son chemin de retour..

 

1quater. Un aspect géométrico-quantique. Ce caractère ajoute à la singularité du tétraèdre régulier, que je rattache aux fermions, particules remarquables par l'individualité de chacune d'entre elles, dans un travail récent. Ce même travail rattache les autres solides considérés, aux bosons.

 

2. Cube. Le résultat final est l'intersection de 3 carrés mutuellement perpendiculaires, formant un trièdre trirectangle de 8 cellules qui sont des octants, où tous les angles dièdres sont des droits 90o. Les faces opposées parallèles en se rapprochant finissent par se confondre 2 à 2 en déterminant un solide d'épaisseur nulle ayant 2 faces; les angles dièdres aux arêtes valent 180o. Les angles polyèdres aux sommets sont simples et d'ordre 1 puisqu'ils appartiennent vraiment à des portions de plans et on peut y reconnaître l'ordre 2 puisque ces portions de plans proviennent de deux plans initialement distincts et devenus virtuels. Il y a une certaine continuïté virtuelle d'une face à la face opposée, à la différence du cas du tétraèdre.

 

3. Rhombododécaèdre régulier sans volume. Les 12 faces sont transportées de façon à contenir le centre du solide, se confondant 2 à 2, elles déterminent 6 plans passant par le centre. Ces plans sont perpendiculaires 2 à 2 et déterminent à eux deux un angle dièdre 90o nouveau pour le rhombododécaèdre régulier. Cet angle est présent dans le RBD régulier, non pas comme dièdre à l'intersection de deux faces, mais à la rencontre ponctuelle de deux faces aux sommets 4.

 

Le RBD régulier sans volume est un hexaèdre, aussi bien que le cube normal. À la différence de ce dernier, ses faces sont des losanges et non des cubes, les angles dièdres sont 60o ou 120o et non 90o. Une autre différence entre eux : le cube normal est un espace 3D fermé et le rhombododécaèdre régulier sans volume n'a aucun espace 3D fermé.

3. Rhombododécaèdre régulier étoilé sans volume 18. Afin de réaliser l'opération de translation des faces, il faut envisager les faces losanges disparues par l'installation des coiffes et les appeler virtuelles. 4 faces triangulaires entourent chacune des faces virtuelles. C'est cet ensemble de 4 faces réelles et d'une face virtuelle qui est soumis au processus de translation décrit. Son centre est au centre de la face virtuelle, hors des faces réelles. Cela ressemble au cas du centre de gravité d'un tore matériel, localisé en dehors de la matière de ce tore. C'est le centre de cet ensemble qui est amené au centre de figure du RBD. Il y a 12 tels ensembles, une fois les translations effectuées, ils dessinent 6 surfaces en partie virtuelles, 2R s'entrecoupant à angle droit, 2V et 2B de même. La figure est donc encore une fois une sorte d'hexaèdre. Elle est une collection de portions de plans s'entrecoupant 6 par 6. Il y a 8 telles collections, selon les permutations de RVBRVB. Elle possède 24 faces triangulaires opposées 2 à 2 par un sommet, 4 par 4 dans un même plan, encadrant une échancrure centrale vide en forme de losange. Chaque face est échancrée dans son plan d'un triangle représentant le tiers de son aire, par l'intersection d'une autre surface de couleur différente. - Si on la complète par les faces virtuelles ci-dessus, la figure a le même nombre de cellules (des quasi-cellules) que celle du RBD sans volume : 24.

 

Le nombre de faces, le nombre de cellules des 4 solides réguliers sans volume.

XXTétraèdre régulier sans volume 13......................N. de faces 4....N. de cellules 14

XXCube sans volume 14.............................................N. de faces 3....N. de cellules.. 8

XXRhombododécaèdre régulier sans volume 17...N. de faces 4....N. de cellules 24

XXRhombododécaèdre régulier étoilé sans volume 18...N. de faces 24....N. de cellules 0....N. de quasi- cellules 24

 

Réversibilité.

Le processus qui, partant du solide S a donné naissance au solide sans volume SSV, peut s'inverser. Il faut inverser les chemins parcourus : en partant cette fois de SSV, on revient à S.

 

Les solides réguliers (14).

Solides normaux, ayant un volume inclus, Nos 1 à 11.

1. Tétraèdre régulier

2. Hexaèdre régulier ou cube

3. Octaèdre régulier

4. Dodécaèdre régulier

5. Icosaèdre régulier

6. Rhombododécaèdre régulier

7. Rhombododécaèdre régulier étoilé

8. Petit dodécaèdre étoilé.

9. Grand dodécaèdre étoilé

10. Grand dodécaèdre

11. Grand icosaèdre

Solides sans volume, Nos 12 à 22.

12. Tétraèdre régulier sans volume

13. Hexaèdre régulier ou cube sans volume.

14. Octaèdre régulier sans volume

15. Dodécaèdre régulier sans volume

16. Icosaèdre régulier sans volume

17. Rhombododécaèdre régulier sans volume

18. Rhombododécaèdre régulier étoilé sans volume

19. Petit dodécaèdre étoilé sans volume

20. Grand dodécaèdre étoilé sans volume

21. Grand dodécaèdre sans volume

22. Grand icosaèdre sans volume

 

Autres solides.

D'autres solides, non réguliers, de prêteraient-ils à des opérations analogues suffisammnt symétriques? Il faudrait examiner le cas du parallélipède.

 

Horizons.

Cette notion peut rendre service. Horizon = famille de plans parallèles, définis par un point sur la sphère des angles solides ou sur la voûte céleste. Un solide a une collection d'au moins 4 horizons. Zénith et nadir sont confondus dans une figuration plane. Il n'y a ici que 6 collections d'horizons, parce que l'horizon d'une face n'est pas altéré par les dérivations décrites :  son agrandissement dans son plan - pour former une coiffe, ou sa translation - pour annuler le volume. La collection des horizons est commodément celle des Nos 1 à 6.

---

 

J'ai réalisé des modèles papier pour les numéros 12, 13, 17 et 18. Figs 1 à 5.

 

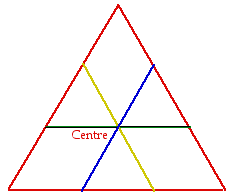
Figs 1, 1bis. Intersec.

Figs 1, 1bis. Voici l'aspect du tétraèdre sans volume. Traces sur la face R de l'intersection des faces J, V et B. Il y a 14 cellules. PrivéTétra1BB.gif

Figs 2, 2bis.

Figs 2, 2bis. Cube sans volume 13. C'est un trièdre trirectangle de 3 carrés se coupant à l'origine. Sur le plan horizontal rose, deux plans s'entrecoupant, ce qui fait 4 cellules supérieures et il y en a autant inférieures, soit 8 cellules au total.                                                                  

Figs 3, 3bis.

Figs3, 3bis. Rhombododécaèdre sans volume 17. C'est un hexaèdre de 6 losanges se rencontrant à l'origine. Les diagonales des losanges sont dans le rapport 1 et racine carrée de 2. L'échelle double en passant de l'image de gauche à celle de droite.

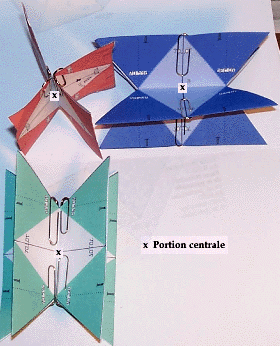
Fig. 4. Rhombododécaèdre coiffé. Rhombododécaèdre coiffé sans volume; les surfaces RVB isolées, avec leurs axes trirectangles. Les portions centrales et les autres portions incolores n'appartiennent pas à la figure théorique. Elles ont un rôle structural dans le modèle. La figure théorique a un vide central. FigX. Vue partielle, montrant le vide central.

Fig. 5. Rhombododécaèdre coiffé sans volume. 1. Patron qui a servi à obtenir la figure X. Chaque grand losange est trichrome RVB. On répète le patron en permutant selon RVB la couleur du petit losange. 2. On découpe, on entaille et on rabat. On assemble.

Un suivi. Quelles conséquences a) pour la théorie géométrique des solides, b) pour la théorie générale des symétries y compris ses applications à la théorie quantique de la matière?

N.B. XI2007. Une rédaction précédente contenait une erreur : j'affirmais que tous les solides normaux 1 à 11 possédaient une version sans volume. J'ai reconnu que certains solides en sont dépourvus : Nos 3, 4, 5; et je réserve ma réponse pour les Nos 7 à 11. - La rédaction erronée a été retirée, son adresse était Système du Québécium. Cinq solides de Platon, 22 solides réguliers. http://www.lisulf.quebec/CinqSPlaton22reguliers.html

-30-