QbStratifNdbis, quebecium.html

Système du Québécium.

Stratification du tableau de Najderek des éléments chimiques.

Pierre Demers

EAPD

5-12I2010

Traduction interdite.

Termes de référence : 

Résumé. Pauwels Najderek a présenté un tableau 2D des éléments chimiques z=1 à 118 ayant des cases en triangles isocèles dallants, où 7 périodes occupent un espace jointivement sans case vide interposée. L’aspect général est celui d’une fer de lance ayant son origine du côté des grandes valeurs de z. Les périodes prennent alternativement la forme d’un losange et celle de deux moitiés de losange opposées par le sommet. Pour les 6 périodes après la 1re, ce tableau démontre qu’elles sont pairées, 2 et 3 ayant chacune 8 cases, 4 et 5 en ayant 18, 6 et 7 en ayant 32. C’est le début d’une organisation en strates Il manque peu de chose à ce tableau pour qu’il présente les éléments z=1 à 120 en 8 périodes et 4 strates bien ordonnées. Dans le tableau résultant, que j’apppelle tableau de Najderek stratifié, chaque élément occupe une case triangle équilatéral, ceux de même quantum l forment des suites continues. Par des pliages, chaque strate 2D passe de 2D à 3D en formant les côtés d’une pyramide à base carrée où les éléments de même valeur de l établissent une couronne carrée; je l’appelle tableau de Najderek stratifié en pyramide à base carrée. Je le transforme encore en  des surfaces de tétraèdres réguliers que j’appelle tableau de Najderek stratifié en tétraèdres réguliers. Le tableau des éléments est alors écrit sur les 16 triangles faces de 4 tétraèdres réguliers. Ainsi apparaît une nouvelle relation entre les formes géométriques fondamentales et l’organisation de l’atome, ajoutant à la théorie platonicienne de la matière. (Najderek a étendu son tableau en lui ajoutant une 8e période  z=119  à 168.  Je m’attache à son tableau de 118 éléments.) La méthodologie en est une de recherche de symétrie dans le cadre du système du québécium

 

Le tableau de Najderek.

Voici ce tableau, daté 1985-2008. Il se fait remarquer par l’usage de 2 dimensions pour figurer chaque période, ce qui le rapproche de la structure en arbre des éléments de Fernando Dufour. Il s’en rapproche encore par l’appel à une géométrie ternaire : Najderek pour la forme triangulaire de ses cases, Dufour pour la forme hexagonale pour ses périodes. Des cases triangulaires suggèrent que la symétrie générale du tableau serait d’ordre 3, alors que celle de la distribution des éléments p l’est effectivement dans chacune des périodes. Réf. 1.

Fig. 1. Tableau original 2D de Najderek (daté 1985-2008). Il contient 118 cases triangles isocèles égaux dont la base est plus longue que les côtés, rapport 150/125Fi1Nd.psd

 

Transformations

Je transforme ce tableau.

1. D’abord, j’établis des cases triangles équilatéraux..

Puis  j’introduis diverses conventions issues du système du québécium.

2. Couleurs. Elles suivent l’ordre RJVB pour les caractères spdf.

3. Déplacements des cases s. Les transformations qui suivent sont plus fondamentales. Déplacement des cases rouges s- et s+ d’une période vers la gauche. Je rapproche Li et Be de H et He. Ainsi Li et Be réunis deviennent la période 2, et la période 3 commencera avec B. Li et Be feront partie de la 1re strate commençant avec H.  Cela revient à considérer H et He comme une paire alcalin alcalino-terreux Les autres paires s-s+ sont également décalées d’une période vers la gauche. La dernière période est numérotée 8.

4. Les cases Fr et Ra étant devenues vides, j’y place les éléments spéculatifs 119Uue et 120 Ubn. Le tableau contient maintenant 120 éléments z=1 à 120 et 8 périodes. Les périodes commencent successivement par H, Li, B, Al, Sc, Y, La, Ac et se terminent sur un alcalino-terreux : He, Be, Mg, Ca, Sr, Ba, Ra et Ubn.

5. Rapprochant les périodes 2 à 2, je fais apparaître des strates : 4 strates de 2 périodes chacune, contenant respectivement 4, 16, 36 et 64 cases, ces nombres valant 4 fois les carrés des 4 premiers nombres. La grille originale est modifiée puisqu’elle contient 120 cases au lieu de 118,

6. À l’intérieur de chaque strate, je réunis les cases selon leur couleur, Je les ordonne selon une rotation numérique dans le sens inverse des aiguilles d’une montre dans chacun des secteurs triangulaires constituants.  Je n’ai pas trouvé moyen de préserver l’ordonnance originale. Il y a 16 secteurs triangulaires chacun une demi-période. Dans un secteur, les spins sont homogènes, les secteurs étant alternativement - et +.

7. Et voilà le tableau stratifié 2D de Najderek. Il affiche des sortes d’hémicycles emboîtés : 8 rouges s de 4 cases, 3 jaunes p de 12 cases, 2 verts p de 20 cases et 1 bleu de 28 cases. Les strates commencent successivement par l’élément H, B, Sc, La et se terminent sur un alcalino-terreux : Be, Ca, Sr, Ubn.

Chaque strate est composée de 4 secteurs d’ouverture 60o.

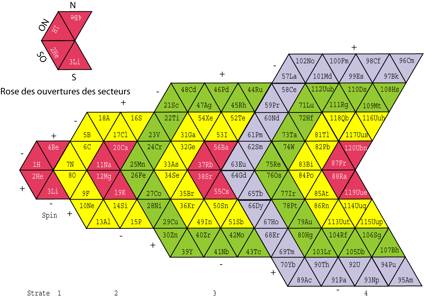
Fig. 2. Tableau de Najderek stratifié 2D en 4 strates. Une strate comprend 4 secteurs triangulaires où le spin est homogène, - ou +. Fi2Nd.png

 

Tableau en surfaces de pyramides.

Ce tableau stratifié 2D se prête à pliages, découpages et collages.

Par pliage et collage, chaque strate 2D passe de 2D à 3D en formant les 4 faces symétriques d’une pyramide à base carrée, où les éléments de même valeur de l établissent une couronne carrée fermée, au même niveau dans chaque strate, homogènes chacune en couleur et en valeur de l..  Il y a 4 couronnes  Le niveau est compté à partir du sommet de la pyramide. Il y a jusqu’à 4 niveaux dans une strate : R, J, V, B.

Le tableau des éléments est alors écrit sur les 16 triangles extraits de la figure 2, devenus faces de 4 pyramides régulières. Noter l’intervention répétée du nombre 4. Le patron avec l’écriture bien orientée apparaît figure 3, les pyramides et les tétraèdres, figure 6.

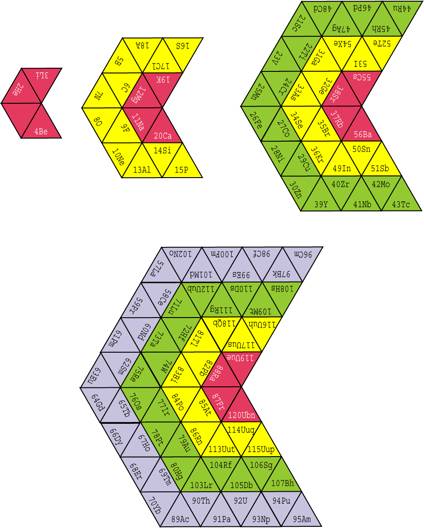
Fig. 3. Tableau 2D devenu 3D sur les faces de 4 pyramides à base carrée.. Patron de découpage de 4 pyramides du tableau affiché sur les faces triangulaires de 4 pyramides régulières à base carrée. Fi3Nd.png

 

Tableau en  surfaces de tétraèdres.

Par pliage. découpage et collage, on obtient des tétraèdres réguliers ayant chacun 4 faces. Les noms des éléments sont inscrits sur la surface de tétraèdres réguliers.

Un tétraèdre par strate, 4 tétraèdres, pas de couronne. Un tétraèdre est incapable d’afficher sur ses faces l’une quelconque des 4 strates sous la forme de couronnes homogènes au complet. Il ne peut afficher tout au plus que les 3/4 de chacune en ne remplissant que 3 de ses faces. La 4e face peut recevoir les cases restantes, mais celles-ci ne s’organisent pas en couronne avec les cases déjà placées.

Cependant, puisque le tétraèdre possède 4 faces triangulaires, il doit pourtant être possible d’afficher sur chacune de ses faces, en une cases sommitale, une des 4 cases rouges de chaque strate, accompagnée des autres cases appropriées. Le tableau des éléments est alors affiché par 120 cases occupant les 16 faces de 4 tétraèdres. Il n’y a pas de couronne, il y a des fragments de couronne. La figure possède une sorte de symétrie, car le schéma d’occupation est répété sur chaque face d’un tétraèdre. Voici le patron de découpage, qui est un grand triangle ayant  2, 4, 6 ou 8 cases de côté, figure 4. Le patron peut aussi prendre l’aspect de parallélogrammes ayant 1 et 2, 2 et 4, 3 et 6 ou 4 et 8 cases de côté, figure 5.

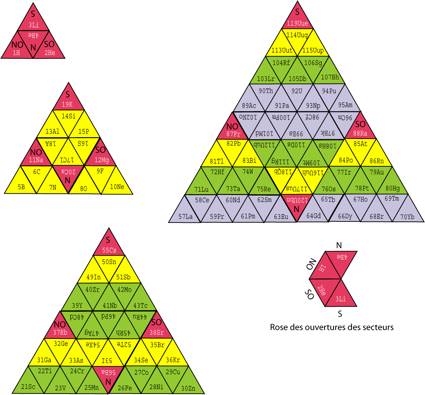Fig. 4 . Tableau 2D devenant 3D sur les faces de 4 tétraèdres. Patron de découpage en 4 grands triangles contenant chacun 3 triangles. Au découpage, on laisse une marge blanche aidant à l’assemblage. Fi4Nd.png

 

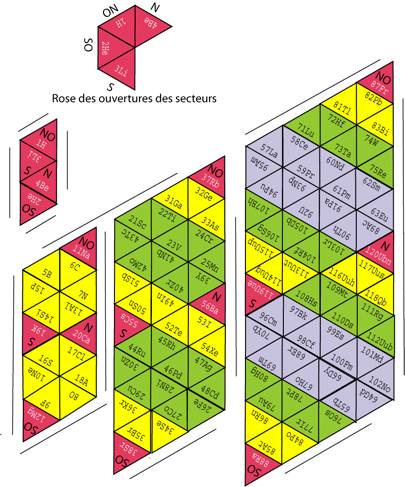
Fig. 5 . Tableau 2D devenant 3D sur les faces de 4 tétraèdres. Patron de découpage en 4 parallélogrammes. Fi5Nd.png

 

J’ai présenté en 1996 des figures comparables aux précédentes et aux suivantes. À cette époque, je n’avais pas encore imaginé les déplacements décrits ci-dessus dans 3. Déplacements des cases s. Aussi 2 cases restaient vides après H et He. Réf. 2.

Je montre comment les grands triangles de la figure 4  peuvent s’assembler en donnant une croix de Malte aux bras inégaux; puis en un très grand triangle pouvant donner un “tétraèdre du québécium” affichant tous les éléments et laissant vides plusieurs de ses 256 cases triangulaires. Figures 6 et 7.

Fig. 6 . Comme la figure 4, les 4 grands triangles sont assemblés contigüment sans case vide. (On peut apercevoir dans la suite continue supérieure de 11 cases rouges un profil de figure avec des lèvres, un nez très proéminent, des yeux et une chevelure...) Fi6Nd .png

 

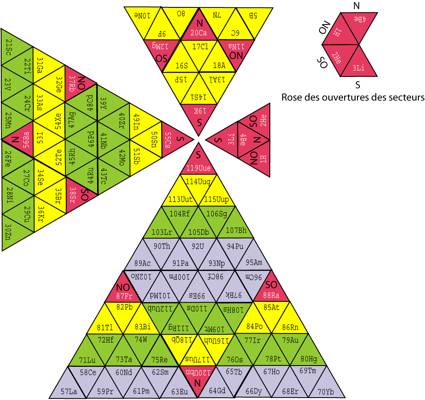
Fig. 7 . Comme la figure 6, les 4 grands triangles sont disposés pour former  une croix de Malte aux bras inégaux. Aucune case vide. Fi7Najderek.png

 

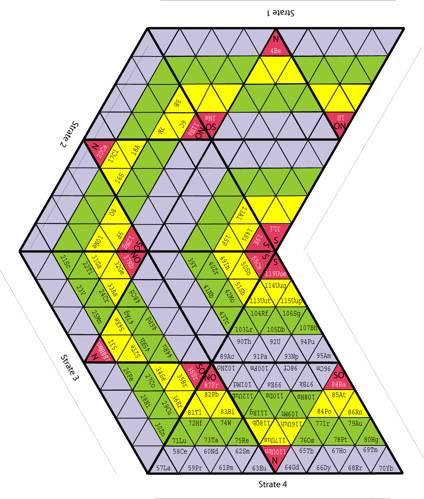
Fig. 8 . Comme la figure 7, mais les 4 grands triangles sont égaux . Elle est source d’une très grande pyramide, affichant tous les éléments sur ses faces triangulaires, comptant au total 16 demi-périodes et 256 cases dont 120 occupées et 136 vides. Fi8Nd.png

 

Fig. 9 . Comme la figure 8. Un très grand triangle contenant 256 cases, source par 3 pliages d’un très grand tétraèdre. Fi9Nd.png

 

Conclusions.

Symétries. Le tableau original de Najderek se prêtait évidemment à des développements de nature physique et mathématiques touchant les principes généraux de conservation et de symétrie; on peut voir là une preuve du bien-fondé de ce tableau au départ. Parti de l’idée de symétries d’ordre 3 liées à des cases triangulaires, je crois avoir montré l’intervention inévitable des symétries d’ordre 4 dans la classification des éléments chimiques.

2D et 3D. Parmi les tableaux nouveaux ici présentés, nécessairement en 2D comme toute surface de papier ou d’affichage, celui de la figure 2 est figuré sur un plan unique, mais rien n’empêche de superposer en 4 niveaux les 4 surfaces de chacune des 4 strates, il devient alors 3D. L’intention des figures 3 à8 est de fournir des patrons qui, une fois employés, donnent des surfaces occupant 3D. De plus, les figures 4 et 5 donnent des tétraèdres, figures enfermant un volume.

Fig. 2 : 2D., peut occuper 3D par superposition.

Figs3 et 8 donnent des pyramides régulières sauf la base carrée occupant 3D.

Figs 4 et 5 donnent des tétraèdres réguliers.

Fig. 6 donnent des portions de pyramides régulières sauf la base carrée occupant 3D.

Fig. 7 est une présentation 2D.

Dans tous les cas, seules des surfaces 2D sont occupées, portant la représentation par un triangle d’un élément.

Les représentations nouvelles que je propose n’épuisent pas la liste des tableaux possibles. Il n’y a pas un tableau idéal unique, il y en a une multitude qui sont tous scientifiquement corrects, mais inégaux devant notre besoin de comprendre la structure de l’atome.

Exceptions. On a procédé comme si tous les éléments avaient une formule électronique régulière, y compris les 19 que l’on sait être irréguliers.

Les règles de la physique quantique. La figure 8 met en évidence un problème de la théorie quantique appliquée à la classification des atomes. Selon cette théorie, les 7 périodes suivant la 1re, celle de H et He, devraient renfermer un grand nombre d’éléments qui n’existent pas. Je suggère qu’il faut chercher une explication dans des règles nouvelles découlant d’une géométrie quantique, faisant partie d’une théorie platonicienne de la matière. Voyez Réf. 3 à 5.

 

Galerie des tableaux 3D.

Fig. 10. Pyramidal en croix de Malte. Fi10Nd.psd

 

Fig. 11. Quatre pyramides, total 120 cases. Une très grande pyramide, 256 cases. Fi11Nd.psd

 

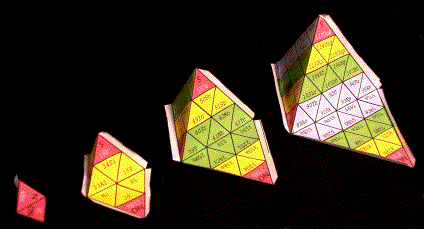
Fig. 12. Quatre tétraèdres, total 120 cases. La face inférieure est déployée pour la rendre visible. Fi12Nd.psd

 

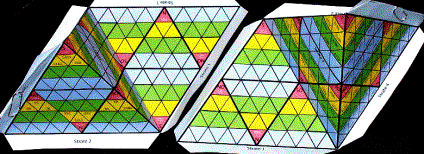
Fig.13. Un très grand tétraèdre, 256 cases. LFi13Nd.psd

 

Remerciements.

Je remercie grandement mon fils Patrick Demers, informaticien, pour son aide assidue dans la préparation de ce document.

 

Références.

1. Pauwels Najderek 1985-2008, arudad@poczta.onet.pl, http://www.egregoralfa.republika.pl/english/newtable.html

 

2. Pierre Demers 1996, Nouveau système périodique des éléments le système du Québécium, ISBN 2-9802454-3-7, PUM, 3e trimestre 1996, non déposé, traduction interdite, pp. 138, 139, 140, Figs 69, 70, Squebecium1996.htm

 

3 Pierre Demers 1997, Nouveau système des éléments le système du Québécium, ISBN 2-9802454-4-5, PUM 4e trimestre 1997, traduction interdite,

 

4. Pierre Demers 2004,  Système du Québécium La nouvelle classification des éléments, ISBN 2-9802454-7-X, PUM 2e trimestre 2004, traduction interdite,

 

5. Pierre Demers 2010,  Système du Québécium, traduction interdite, site : http://www.lisulf.quebec/quebecium.html

-30-