QbSyst2e.27.html
Syatème du Québécium
Suivant QbSyst2e.28.html à venir. Merci critiques commentaires.
Précédent
QbSyst2e.26.htmlReproduction permise avec mention d'origine.
Traduction interdite.
Chapitre 20
Commentaires sur l'arbre des éléments (ElemenTree) de Fernando Dufour
par Pierre Demers
mars 2004

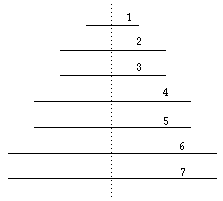
FIG. 1. Schéma de l'arbre des éléments : vue de côté, les plateaux et les périodes.
Présentation
L'arbre des éléments ou "sapin périodique" est une structure tridimensionnelle formée d'un pylône haut de 27 cm et de plateaux inégaux de contour hexagonal, le plus grand étant situé en bas et ayant près de 20 cm de diagonale.
Les alcalins et les alcalino-terreux, ainsi que l'hydrogène,, apparaissent sur le pylône, les autres éléments, période par période, sur les plateaux.
Originalité
L'originalité de l'arbre des éléments est de distinguer le caractère des éléments selon la distance entre sa case, où est inscrit son symbole, et l'axe de l'arbre. Il semble que l'arbre des éléments ait été le premier à présenter une telle organisation, et les commentateurs précédents ne l'ont pas signalé.
Schématiquement, le caractère d'un élément est défini par celui de son électron caractéristique ou de valence, et celui-ci a l'un de 4 caractères, décrits par les lettres s, p, d ou f ou par la valeur de l, quantum azimutal. (C'est le caractère quantique azimutal).
Distance de l'axe = caractère de l'élément
distance 0 = caractère s, l= 0
distance 1 = caractère p, l = 1
distance 2 = caractère d, l = 2
distance 3 = caractère f, l = 3
Deux dimensions sont évidemment insuffisantes puisque l'on veut garder ensemble les éléments de chaque période. En effet, les mêmes caractères se rencontrent dans plus d'une période. Chaque période requiert les 2 dimensions d'un plateau, passer d'une période à l'autre requiert une 3e dimension.
De plus, chaque fois que des éléments d'un caractère se présentent dans une période, leur nombre est le même.
Éléments s : il y en a 2
Éléments p : il y en a 6
Éléments d : il y en a 10
Éléments f : il y en a 14
On aperçoit là la possibilité de superposer selon des colonnes verticales les cases de même caractère et de périodes différentes.
La distance 0 est celle des éléments figurant sur le pylône. Le cas de l'hélium est une dérogation à l'analyse que nous présentons ici, l'auteur de l'arbre des éléments ayant préféré le placer seul sur un plateau 1. Notre analyse est basée sur la structure de l'atome.
Distance 1 : celle des cases p formant un hexagone.
Distance 2 : celle des cases d placées dans une couronne de 12 cercles.
Distance 3 : celle des cases f placées dans une couronne de 18 cercles. FIG. 2.
On voit que les cases d et f occupent incomplètement les cases de leurs couronnes respectives.
Voici comment les éléments sont répartis sur les plateaux de l'arbre. FIG. 2 à 9.
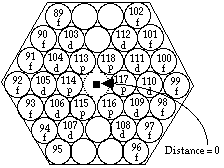
FIG. 2. Plateau et période 7. Les cases s sont sur l'axe, distance 0;
les 6 cases p forment 2 lignes brisées de 3 cases chacune;
les 10 cases d, 2 lignes brisées de 5 cases chacune;
les 14 cases f, 2 lignes brisées de 7 cases chacune.
Les éléments s (soit 87 et 88), sont inscrits à la distance 0, sur le pylône.
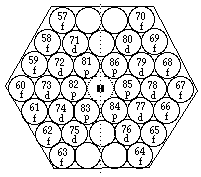
FIG. 3. Plateau et période 6. Comme plateau et période 7 sauf les valeurs de z.
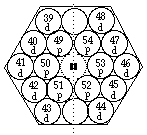
FIG. 4. Plateau et période 5. Comme plateau et période 7 sauf les valeurs de z et l'absence de cases f.
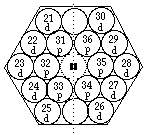
FIG. 5. Plateau et période 4. Comme plateau et période 7 sauf les valeurs de z et l'absence de cases f.
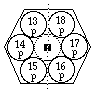
FIG. 6. Plateau et période 3. Comme plateau et période 7 sauf les valeurs de z et l'absence de cases d et f.
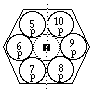
FIG. 7. Plateau et période 2. Comme plateau et période 7 sauf les valeurs de z et l'absence de cases d et f.
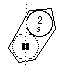
FIG. 8. Plateau et période 1. Par exception, le plateau 1 ne porte qu'une case, et une case s, celle de He qui est un élément s.
Symétries et critiques
Recherchant la symétrie dans la classification, au moins 3 critiques se présentent. Elles ajoutent aux commentaires de Scerri, Lemelin et Perreault
1. Éléments sur le pylône. Placer les éléments s ailleurs que sur les plateaux suggère qu'il existerait une discontinuïté importante entre ces éléments et les éléments p, d et f. Or cette suggestion n'a pas de justification chimique ou électronique et elle induit en erreur. Ainsi, les électrons de valence s et p du carbone sont indiscernables, concourant à donner les 4 valences égales bien connues : c'est le carbone tétraédrique.
2. Cases vides. Au total, 16 cases sont vides. On peut voir là un pas dans la bonne direction, puisque, dans le tableau traditionnel de Mendeleev, 36 cases restent vides. Mais l'idéal serait de n'avoir aucune case vide.
On souhaiterait mettre à profit une forme géométrique qui ne laisserait aucune case vide. Tant que cela n'est pas réalisé, la question (naïve, instinctive, naturelle) se pose : pourquoi y-a-t'il des cases vides?
3. Passage à 2D. Il n'y a pas de moyen immédiat de transformer la classification 3D de l'arbre des éléments en une classification 2D.
Si on place côte à côte les plateaux des périodes 1 à 7, il manque 13 éléments inscrits sur le pylône, qui restent de côté.
Telle qu'utilisée dans l'arbre des éléments, la géométrie du nombre 6 n'est idéalement ou parfaitement adaptée à la classification que dans les périodes 2 et 3 et pour les atomes p.
Une classification des éléments qui réaliserait "cette belle symétrie qui accompagne toujours la vérité" (dixit André Lemelin, 1995), voilà l'idéal restant à trouver.
Le système du québécium représente un essai dans ce sens.

FIG. 9. Dans le système du québécium, une période occupe 2 grilles carrées égales et opposées, où les éléments de même caractère dessinent des équerres des divers caractères : f, d, p et s, ces dernières étant réduites à une seule case. Les quadrants occupés sont NO et SE.
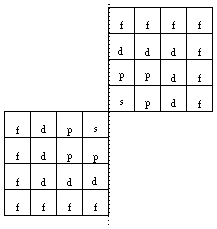
FIG. 10. Les 2 grilles de la figure précédente , disposition alternative occupant les quadrants SO et NE.
Passer de l'arbre des éléments au système du québécium
Dans le système du québécium : (FIG. 9)
1. les périodes occupent 2 grilles carrées opposées et
2. les éléments des divers caractère y occupent une équerre, ligne brisée à 90o. (Équerre réduite à une case unique dans le cas des éléments s).
On peut apercevoir dans l'arbre des éléments une construction intermédiaire (intermédiaire, parce qu'on imagine, comme point de départ ou de référence obligé, le tableau traditionnel de Mendeleev), conduisant aisément, par une transformation bien choisie, à l'organisation du système du québécium :
1. sur les plateaux, les périodes occupent 2 losanges complets opposés, si l'on y inclut une case vide et
2. les éléments de chaque caractère y occupent une ligne brisée à 120o.
Le passage peut se décrire géométriquement, par exemple sur la période 7. Dans une première opération, on sépare les losanges. FIG. 11.
Dans une 2e opération, on fait pivoter les losanges de 30o autour de l'axe. Dans une 3e opération, on transforme par glissement au contact les losanges en carrés. FIG. 12.
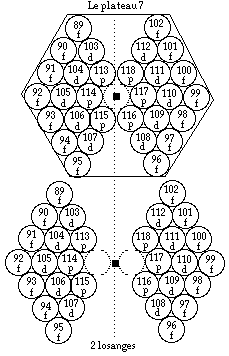
FIG. 11. Période 7. L'arbre des éléments et sa transformation.
En haut : le plateau 7. On y reconnaît 2 losanges ayant une case commune.
En bas : on a séparé les losanges.
Continuez à la figure suivante.
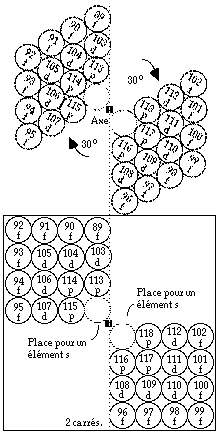
FIG. 12. Période 7. Suite. En haut : on a fait pivoter les losanges de 30o dans leur plan autour de l'axe. En bas, on a remplacé l'arrangement interne en losanges par un arrangement en carrés. En plaçant les éléments s, on retrouve une figure précédente montrant la période 7 au complet dans le système du québécium. FIG. 9.
Les 2 cases vides sont disponibles pour les 2 éléments s de la période.
Dans ce passage, la géométrie de nombre 6 est devenue celle du nombre 4.
La période 7 occupe incomplètement un carré de côté 8 cases et les quadrants SO et NE sont vides. On peut aussi bien la loger dans les quadrants SO et NE (FIG. 10) et alors les quadrants NO et SE sont disponibles pour recevoir la période 6. Les périodes 6 et 7 ainsi réunies forment une strate.
La classification du québécium comporte 4 strates, contenant respectivement 2, 16, 36 et 64 éléments. Il n'y a que 2 cases vides sur 120, et dans les versions récentes, il n'y en a aucune.
Ces strates peuvent être disposées 3D l'une au dessus de l'autre ou placées 2D côte à côte à volonté. FIG. 13.
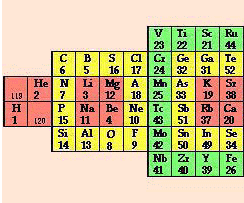

FIG. 13. Classification des éléments dans le système du québécium. Deux cases sont vides dans cette version. Voyez
www.quebecium.qc.caRéférences
1. Charles Janet 1929
http://web.ccr.jussieu.fr/tarantola/Files/Professional/Mendeleev/Janet_1929.pdf
2. Paul-Émile Giguère (1965)
Tableau périodique 3D
http://chemlab.pc.maricopa.edu/periodic/giguere.html

FIG. 14. Le tableau de Giguère; 4 tablettes, 8 faces, les annotations sont de nous. H et He absents.
3.Glenn T. Seaborg 1969, 1989,
Chem. News
4. Francis Perrin 1973, 1974,
C. r., 1973.
Sc. et Avenir, 1974, 192, 24-26.
5. Fernando Dufour 1979
An attempt to unravel atomic structure with a three-dimensional model of the periodic table,
Thèse de maîtrise, Université Concordia, Montréal
6. Fernando Dufour 1981, 1982,
La classification des éléments et la molécule spdf,
Spectre, revue de l'APSQ Association des professeurs de science du Québec,
11, 1, 22-28, octobre 1981*;
11, 2, 45-56, décembre 1981;
11, 3, 5-9, mars 1982.
*introduction de Gilbert Lannoy
7. Carole Thibaudeau 1982.
La molécule spdf de Fernando Dufour : outil scientifique et pédagogique.
La Presse, jeudi 27 mai
7bis. Marc Tison 1994
Un tableau périodique en trois dimensions
Un Québécois réinvente l'outil de base de la chimie
Le Devoir, mercredi 20 avril 1994
8. André Lemelin 1995,
De l'ordre dans le tableau (tableau de Fernando Dufour)
Québec-Science, 34, 3, 36, novembre
Il y a deux méthodes de classement : par la périodicité des propriétés chimiques et par la structure de l'atome.
... le tableau périodique est demeuré un monument inachevé - sans doute le seul parmi les grands édifices de la science à ne pas arborer cette belle symétrie qui accompagne toujours la vérité.
9. Eric Scerri 1997, 1998
La classification périodique des éléments,
Pour la Science n° 253 novembre 1998
(American Scientist, nov.-déc. 1997, 546-553,
Scientific American, sept. 1998, 78-83)
10. Mathieu Perreault 2003,
La beauté du tableau périodique (Le tableau en 3 dimensions de Fernando Dufour),
La Presse, Actuel 8, dimanche 23 novembre
11.
http://agora.qc.ca/mot.nsf/Dossiers/Tableau_periodiquehttp://mendeleiev.cyberscol.qc.ca/carrefour/objets/tableauxarbredates-dufour.jpg
http://agora.qc.ca/mot.nsf/Dossiers/Fernando_Dufour
12. George B. Kauffman
http://chemeducator.org/bibs/0004003/00040308.htm
13. Un répertoire exhaustif (sauf silence sur les travaux de Janet, de Dufour et de Demers…)
http://www.chemistrycoach.com/periodic_tables.htm#Periodic%20Tables%20of%20Historical%20Interest
14. J. P. Serodino
http://perso.wanadoo.fr/j.p.serodino/francais/index/ch4/Resume_ch4.htm
15. Pierre Demers , 1995...
Le système du Québécium
www.quebecium.qc.ca
et les liens
----------------------------------------------------------------------
Observations sur l'article d'André Lemelin
Cet article me paraît être la tentative d'analyse la plus sérieuse parue sur l'arbre des éléments. Cependant, certains de ses passages me semblent inexacts et demanderaient correction ou éclaircissement.
1. ".. il n'est tout simplement pas possible d'intégrer correctement" les lanthanides et les actinides "dans un tableau 2D".
Or ils sont intégrés fort bien dans le tableau de Francis Perrin 1973, Glenn Seaborg 1969, et déjà dans le tableau de Charles Janet 1928-1929.
2. "La plus grande innovation de mon modèle, dit Fernando Dufour, est de révéler la nature gémellaire du système périodique".
Fernando Dufour aurait-il été le premier à signaler cette nature gémellaire? Elle est pourtant très apparente dans les tableaux de Perrin 1973 , de Seaborg 1969 et Janet 1929.
3. "Sur les disques, la spirale fait autour de l'axe des boucles"..."à mesure que croît le nombre atomique et la charge énergétique des éléments".
Qu'est-ce que la charge énergétique des éléments?
On trouve une quantité appelée charge énergétique dans une référence sur l'électromagnétisme. Mais elle n'a rien à voir avec la classification des éléments. Serodino.
4. "... l'arbre périodique tient compte de tous les électrons de chacun des éléments", alors que dans les meilleurs tableaux périodiques "le classement est conforme aux seuls électrons de valence".
Affirmation gratuite et incompréhensible. Dans l'arbre des éléments comme dans les meilleurs tableaux périodiques, la place de chaque élément est définie par le caractère de l'électron caractéristique ou de valence.
5. "Plus on descend le long de l'axe, plus le niveau de l'énergie est élevé..."
Comment définit-on ce niveau de l'énergie?
On sait très bien que l'atome d'hydrogène possède des états ayant des niveaux d'énergie divers. Voudrait-on confondre la succession des éléments avec cette succession d'états de l'atome d'hydrogène?
6. "Si l'on fait face à l'axe s, on remarque que tous les symboles des éléments placés sur la gauche sont entourés d'un cercle (ou d'un carré) épais, montrant leur électronégativité (ils gagnent un électron), tandis que ceux qui se trouvent à droite sont entourés d'un cercle fin, indiquant leur électropositivité (la perte d'un électron). C'est la symétrie horizontale de l'arbre".
Il serait correct de dire que les éléments de gauche ont un spin d'un signe et ceux de droite, un spin de l'autre signe. Il s'agit du spin de l'électron caractéristique ou de valence. Il ne faut pas confondre électropositivité et électronégativité d'une part et signe du spin d'autre part.
7. La figure du modèle de M. Dufour est inversée droite-gauche et il est difficile d'apercevoir comment faire face à l'axe s, ce qui est demandé à l'observation précédente.
8. "Jusqu'à maintenant ... le tableau périodique est demeuré un monument inachevé..."
L'auteur voudrait-il dire qu'avec l'arbre périodique des éléments, le monument serait désormais achevé?
------------------------------------
Le présent document, destiné à la publication, est communiqué en premier lieu à Fernando Dufour, André Lemelin, Québec Science, Gilbert Lannoy et Mathieu Perreault. Leurs réponses m'intéresseraient beaucoup.
Pierre Demers c3410@er.uqam.ca 27 mars 2004
André Lemelin andre.lemelin@sympatico.ca
Mathieu Perreault, mathieu.perreault@lapresse.ca
Québec Science,
courrier@QuebecScience.qc.ca4388 rue Saint-Denis, bureau 300, Montréal H2J 2L1
QbSyst2e.27.html
Syatème du Québécium
Suivant QbSyst2e.28.html à venir. Merci critiques commentaires.
Précédent
QbSyst2e.26.html![]()