QbtetraNveau.doc

Système du Québécium.

Le tétraédre dans la classification des éléments chimiques. Une note historique. Une version nouvelle du tableau tétraédrique des éléments.

Pierre Demers

EAPD

12-26I2010

Traduction interdite.

Termes de référence :

Résumé. La publication par Tsimmermann d’un tableau tétraédrique des éléments chimiques daté de 2007 me suggère de rédiger la présente note d’antériorité pour faire mieux connaître mes propres travaux originaux à ce sujet, qui remontent à 1996. J’ajoute la présentation d’une version originale d’un tel tableau. La méthodologie en est une de recherche de symétrie dans le cadre du système du québécium.

Tsimmermann.

Je remarque avec intérêt la contribution de Tsimmermann en 2007 et en 2008 décrivant la possibité de recourir au tétraèdre pour classifier les éléments chimiques. Il montre des tableaux des éléments chimiques dont les constituants graphiques sont inscrits dans un tétraèdre régulier. Ces constituants sont soit 4 rectangles portant chacun des inscriptions 2D, soit des sphères. Le tétraèdre régulier est dépourvu de faces parallèles, mais il contient 3 paires d’arêtes disposées mutuellement à angle droit. On peut tracer un plan parallèle à chaque arête d’une telle paire, et il rencontre 4 faces pour y inscrire un rectangle. Figs 1 et 2. La figure 3 présente les écritures 2D.

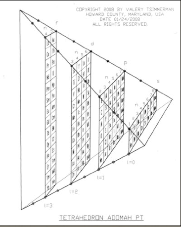
Fig. 1. Les structures tétraédriques publiées par Tsimmermann. Dans celle-ci, 120 éléments sont figurés sur des rectangles inscrits dans un tétraèdre. La perspective paraît incorrecte si les cases sont des rectangles comme à la figure 3. Elle serait correcte si les cases sont des carrés et alors le tétraèdre est irrégulier: l’arête de droite est la moitié de chacune des 5 autres. Les espacements entre les rectangles valent les 2/9 de la distance entre l’arête verticale et l’arête horizontale opposée.Cette figure est reprise plus loin. tetraTsimm.png (cgi)

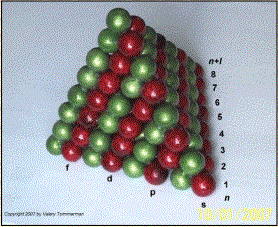
Fig. 2. Les structures tétraédriques publiées par Tsimmermann. Dans celle-là, 120 éléments sont figurés par des sphères associées en un tétraèdre. Réf. 1, Tsi2007.psd (cgi)

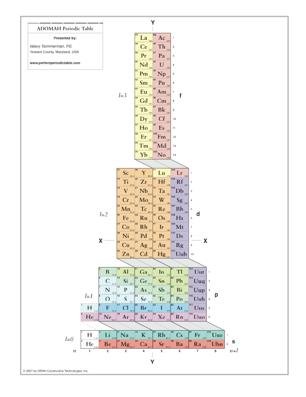
Fig. 3. (Tableau périodique Adomah). On trouve ici en géométrie 2D le contenu des tablettes de la figure 1, les cases sont ici des rectangles dont la base vaut le double de la hauteur. On remarque un doublon celui des cases H et He. ADOMAH Table v2Ts.pdf

Cette contribution m’intéresse parce que confirmant ce que j’ai signalé dès 1996 : la nécessité de recourir à la géométrie du tétraèdre et plus généralement à la symétrie d’ordre 4 pour comprendre la classification des atomes et leur organisation. Or cet auteur ne mentionne pas mes contributions.

Un Tétraèdre du Québécum. Dès 1996, j’ai présenté un tétraèdre du Québécium mettant à profit ses 4 faces pour inscrire le tableau des éléments. Puisque le tétraèdre a 4 faces, il est naturel d’attribuer une face à chacune des 4 strates en lesquelles je classifie les éléments. De plus, les cases choisies étaient des triangles, capables de paver chaque face d’un tel tétraèdre. La 4e strate, ayant 64 cases, remplit exactement une face d’un tétraèdre ayant 256 cases. Les autres faces comprennent des cases vides. Fig. 4. Réf. 2, 3.

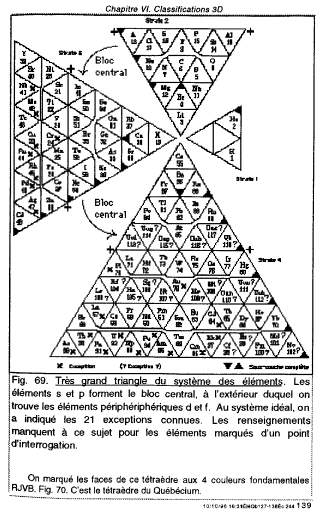
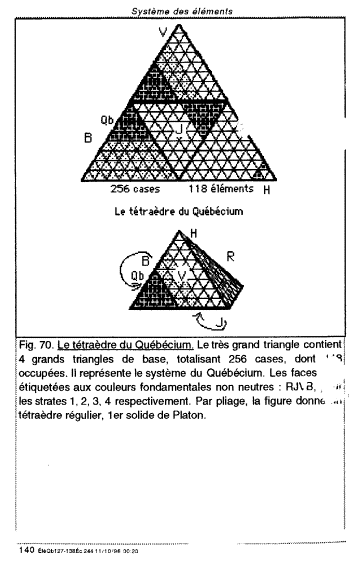
Fig 4. Dans ces pages, datées de septembre 1996, je présente un tableau tétraédrique des éléments. Réf. 2

Fig. 5. Cette page publiée en 1997 de mon travail. soumis en 1996, présente un tableau tétraédrique des éléments. Réf.3

J’ai aussi présenté en 1997 un tableau 3D formé d’un assemblage de 120 sphères en tétraèdre régulier, les 4 strates spdf correspondent aux couleurs RJVB. Fig 6.

Fig. 6. Cette page montre une face d’un tétraèdre formé de sphères assemblées tableau 3D des 120 cases sphériques. 1997. Réf. 4.

J’ai réalisé un tableau 3D tétraédrique de 120 boules colorées. Quatre strates spdf aux couleurs RJVB. Avant le 8 décembre 1998 selon mes notes. Fig. 6.

Fig. 7. Tableau 3D tétraédrique de 120 boules colorées inscrit dans une boîte cubique de côté extérieur 14 1/16. Strates 1234, éléments spdf aux couleurs RJVB. Avant le 8 décembre 1998. Tetraboules26I2010.png

Depuis 1995, j’ai développé une géométrie quantique utilisant le tétraèdre et la symétrie d’ordre 4 pour comprendre la classification et l’organisation des atomes. Consulter Réf 6, 13 à 16.

Autres références au tétraèdre.

La publication de Tsimmermann contient des références à l’application du tétraèdre à la théorie du noyau, par exemple Garai. Réf. 12.

Version nouvelle du tableau tétraédrique des éléments 2010.

Donnant une suite à ma publication précédente Réf. 9 (sur la stratification du tableau de Pauwels Najderek Réf. 8), j’en reprends la figure 7, et je récris chacune des strates en distribuant les éléments dans les cases triangulaires selon le schéma de ma figure 324.

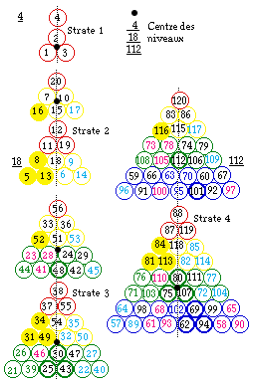
Fig. 8. Distribution des120 éléments par tétrades dans les strates. Chaque strate occupe ici 2 niveaux. Niveau supérieur: cases triangulaires pointant vers le bas, niveau inférieur, vers le haut. C’est ma figure 324 du 6 VI 2003.

,http://www.lisulf.quebec/QbS2Fig324. gif

Le résultat apparaît aux figures 9 et 10. Les ombrés sont inégaux pour suggérer que le plan portant la strate est plus ou moins élevé au dessus de la feuille de papier supposée horizontale. La strate 4 repose sur cette feuille. Puis les strates sont superposées avec un espacement vertical uniforme que suggèrent les ombrés accompagnant les strates 1, 2 et 3, de manière à s’inscrire dans un tétraèdre régulier. L’espacement vertical vaut le côté de la strate 1. La hauteur du tétraèdre vaut 86,6% du côté de la strate 4. Elle peut être exagérée pour motifs de visibilité.

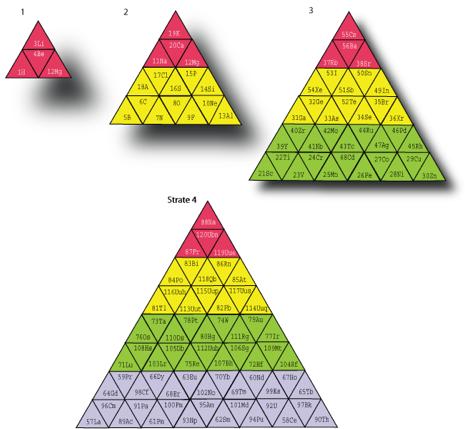
Fig. 9. Les strates remplies correctement de 30 tétrades. Fi16Nd.ai (cgi)

Fig. 10. Tableau tétraérique des éléments 2010. Les 4 strates inscrites dans un tétraèdre régulier, vue plongeante. En 3D, les 6 arêtes sont de longueurs égales. Fi15Nd.ai (cgi)

Appendice 1. Apport original de Tsimmermann; stratification de ses tableaux.

La succession connue des éléments.Tsimmermann a apporté certains progrès originaux à la théorie de l‘atome en recourant à la géométrie du tétraèdre et à des considérations d’esthétique et de symétrie. Il a déclaré que le remplissage du tétraèdre impose des règles de sélection exigeant la succession connue des éléments, jusqu’ici décrite partiellement sous les noms des «régles» empiriques de Madelung et de Hund.

Je résume.

1. Madelung : dans une période, la somme n+l reste constante.

2. Hund: à n et l donnés, il ya succession ininterrompue des spins – d’abord, puis des spins +.

3. Et il faut ajouter une affirmation: la succession des valeurs de n+l forme la suite 2, 8, 8, 18, 18, 32, 32, total 118 dans le tableau classique de Mendeleev et la suite 2, 2, 8, 8, 18, 18, 32, 32, total 120 dans les tableaux du système du québécium.

J’ai examiné cette question de la succession connue des éléments plusieurs fois en utilisant surtout la géométrie 2D de la grille du québécium, qui est équivalente à celle du tétraèdre. J’en arrive à me dispenser de toute référence aux valeurs énergétiques des niveaux de l’atome d’hydrogène. Entre autres Réf. 17.

La figure 1 refaite. Je montre d’abord la figure 1 refaite 3D dans les figures 11 et 12, démontrant le bien-fondé de la figure1.

Fig. 11. On a refait la figure 1, cette fois en 3D vraies, avec des cases rectangulaires sur 4 cartes l=0, 1, 2, 3. Ceci confirme l’intention de Tsimmermann. La diagonale d'une face de la boîte cubique mesure 24 cm, aussi bien qu’une arête du tétraèdre. Adoboite0123.html

Fig. 12. On a supprimé les faces du tétraèdre figure 11, afin de dégager la vue. Adobaguettes0123.psd

Fig. 13. De la figure 11, on supprimé les cartes l=1 et 2 afin de dégager la vue de la carte l=3. Le tracé rouge désigne la strate 1, le tracé bleu, ce qui reste de la state 4. (La strate 4 contient aussi des portions des cartes 1 et 2). Adoboite0314.psd

Stratification des tableaux de Tsimmermann. Il est assez facile de transformer en un tableau stratifié les tableaux des figures 1, 2, 3.

Voici une étape intermédiaire réalisée par un réalignement de la figure 3, en conservant les cartes selon la valeur du quantum l = 0, 1, 2, 3. On a inscrit Qb au lieu de Uuo et a supprimé un doublon H. Figs 14, 15.

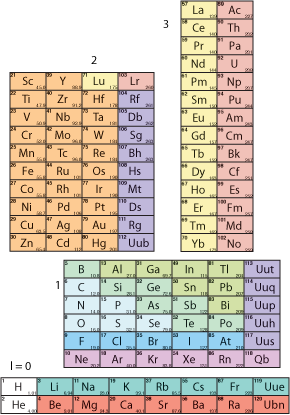
Fig. 14. Voilà les 4 cartes selon le quantum l = 0, 1, 2, 3, tirées de la figure 3. 4pourbiseau.ai (png)

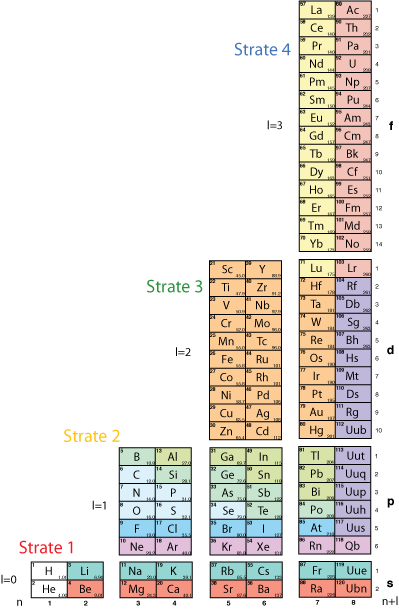
Fig. 15. Voilà les cartes de la figure précédente assemblées avec justification à droite puis organisées en 4 colonnes larges de 2 cases. Chaque colonne est une strate. Adomah2.ai (png)

La composition des strates est identique à celle montrée en tétrades dans la figure 8 ci-dessus. En poursuivant les opérations on arrive naturellement au Tableau tétraédrique des éléments 2010 de la figure 10.

Remerciements.

Je remercie grandement mon fils Patrick Demers, informaticien, pour son aide assidue dans la préparation de ce document.

Références.

1.Valery Tsimmermann 2008, http://perfectperiodictable.com/novelty.html

Je remarque l’assurance de cet auteur : (tableau périodique parfait…); l’évocation d’une tradition biblique hébraïque; toutes les références sont en anglais. Pourquoi Adomah ?

(Il a été nommé Tableau périodique Adomah à cause de l’histoire biblique de la création du 1^er homme, faite à partir de la poussière de la terre… Adomah vut dire Adam en hébreu.)

2. Pierre Demers 1996, Nouveau système périodique des éléments le système du Québécium, ISBN 2-9802454-3-7, PUM, 3e trimestre 1996, non déposé, traduction interdite, pp. 138, 139, 140, Figs 69, 70,. Pierre Demers 2010, Système du Québécium, traduction interdite. http://www.lisulf.quebec/Squebecium1996.htm

3. Pierre Demers 1995-1997, Nouveau système périodique des éléments. Treillis et couplageSS. Affinités biologiques. a) Communication soumise au XVe congrès international de biomathématique, 6, 7 et 8 septembre 1995, Kremlin-Bicêtre (France).

b) II, R.Biomath., 34, 138, 5-32, 1997. Ms daté du 23 février 1996.

4. Pierre Demers 1997, Nouveau système des éléments le système du Québécium, ISBN 2-9802454-4-5, PUM 4e trimestre 1997, traduction interdite.

5. Pierre Demers 2004, Système du Québécium La nouvelle classification des éléments, ISBN 2-9802454-7-X, PUM 2e trimestre 2004, traduction interdite.

6. Pierre Demers 2010, Système du Québécium, traduction interdite, site : http://www.lisulf.quebec/quebecium.html

7. 875 Pierre Demers 1998, Le tétraèdre du Québécium No 1721, section physique 66e congrès de l'ACFAS, Univ. Laval, 12 mai 1998, Présenté avec l'assistance de Louis de Kinder.

8. Pauwels Najderek 1985-2008, (Un nouveau tableau périodique des éléments chimiques), arudad@poczta.onet.pl, http://www.egregoralfa.republika.pl/english/newtable.html

9. Pierre Demers 2010, Stratification du tableau de Najderek des éléments chimiques.

http://www.lisulf.quebec/QbStratifNdbis.htm

10. Jonathan Demers et Manuel Magnan, Québécium, (personnages-éléments), 2002, http://mendeleiev.cyberscol.qc.ca/carrefour/personnages/inertes/QbJDemers.html

11. Pierre Demers 2004, Chapitre 17. Application à la classification des élémentsTableaux 3D, 16III2007

http://www.lisulf.quebec/QbSyst2e.24.html

12. Jozsef Garai 2003, http://lanl.arxiv.org/abs/nucl-th/0309035.pdf

13. Michel Nguyen The 2001, Compte rendu de la rencontre du Québécium du mercredi 5 septembre 2001,

http://www.lix.polytechnique.fr/~mnguyen/Quebecium/qc_5_9_2001.html

14. 861, 1403 Pierre Demers 1997, Symétries d’ordre 4 dans le système des éléments et couplage SS, ACFAS, 65e congrès, UQTR, mai 1997, Présenté avec l'assistance de Louis de Kinder.

15. 862 Pierre Demers 1997, Nouveau système des éléments. Le Québécium, élément 118 et son vêlage, ACFAS, 65e congrès, UQTR mai 1997. Présenté avec l'assistance de Louis de Kinder.

16. 875 Pierre Demers 1998, Le tétraèdre du Québécium,No 1721, section physique 66e congrès de l'ACFAS, Univ.Laval, 12 mai 1998. Présenté avec l'assistance de Louis de Kinder

17. 1015 Pierre Demers 2009 Système du Québécium. Confection du tableau des éléments par écriture des valeurs de n. 4IV2009.2 Cconfectab.htm

-30-