QuadrupleMiroir

Système du Québécium.

Le tableau périodique des éléments est un quadruple miroir.

Pierre Demers

29 III – 3 IV 2010

Traduction interdite.

Termes de référence : 

Résumé. Je propose des figures et des photos prises avec des mirors des tableaux périodiques des éléments issus du système du québécium : semi-elliptique, elliptique, quart d’ellipse.

 

Les tableaux.

1. Le tableau périodique de Mendéléev des éléments chimiques récrit dans le système du québécium donne plusieurs tableaux. Le 1^er dans l’ordre logique est semi-elliptique. On lui trouve une symétrie miroir (un miroir) unique aligné selon la ligne horizontale. Figs 1 et 2.

Le miroir obtenu préserve les valeurs et les emplacements de l, reconnaissables par leurs couleurs. Il préserve aussi les valeurs de m et le spin s. Quant à z et n, leurs valeurs changent de +-1. Toute strate est organisée selon z, n, s, l, m d’après un plan universel décrit Fig. 3.

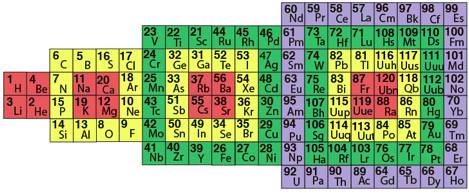
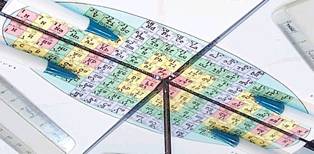
Fig. 1. Le tableau semi-elliptique. Image 27.png jaune

 

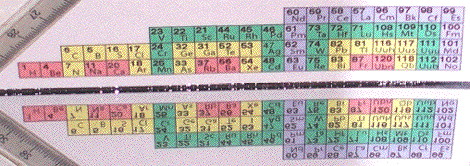
Fig. 2.  Image obtenue à l’aide d’un miroir dièdre dont un seul plan est utilisé. L’original papier est le demiant N de la figure 1. Image 21.png jaune

 

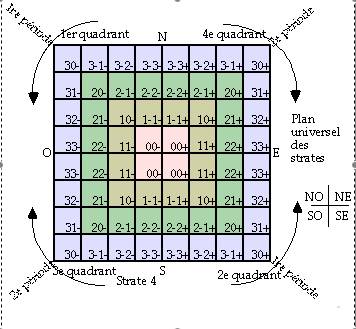
Fig. 3. Plan universel de l’organisation quantique de toute strate. Les symboles sont lms, BVJR pour fdps. Une strate complète n’enferme aucune couronne vide. Selon le numéro de la strate, les couronnes B, V et J peuvent être inocccupées. Les flèches décrivent l’occupation progressives par valeurs croissantes de z. Les effets miroirs discutés Figs 1 et 2 s’opèrent autour des axes de l’un des axes NS ou OE ou des 2.  Voyez la discussion 2D ou 3D? Relativités. en fin du plus loin. Image 36 jaune

 

2. Puis le tableau elliptique, qui présente une symétrie d’ordre 4 équivalente à 2 miroirs croisés au centre de figure, comme j’en ai discuté dans un travail précédent avec figure à l’appui. Réf. 1.  Ce tableau étant contenu dans un plan, les 2 miroirs peuvent être réduits à 2 droites orientées selon les points cardinaux. Les opérations miroirs NS et OE ne sont pas interchangeables puisque le tableau est elliptique càd, s’inscrit dans une ellipse plutôt qu’un cercle. Ces opérations donnent naissance à 3 quadrants de 30 cases-éléments à partir de l’original. Figs 4 et 5.

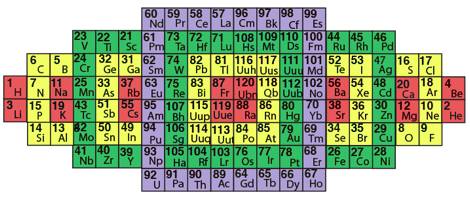
Fig. 4. Tableau elliptique. Image 32.png jaune

 

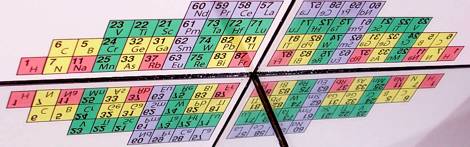
Fig. 5. Comme Fig. 6 ci-dessous. Image 35bis.png jaune

 

.............................................. ..........Nord

Sud...........................

Fig. 6. Photo mettant en œuvre un dièdre de miroirs d’axe vertical. L’original papier est le quadrant NO d’un tableau elliptique, en haut à gauche. Les réflexions conservent les valeurs de l, qui sont marquées par les couleurs (0123, spdf, RJVB) et celles de m. Les valeurs de s, z et n s’ajustent. Extrait de Réf. 1 Fig. 62.

 

3. Du tableau 2D semi-elliptique ci-dessus, on peut isoler les strates et les superposer avec espacements en un tableau 3D. On part d’un original papier des quadrants NO. Un dièdre de miroirs de traces NS et OE reconstitue le tableau complet comme dans les figures précédentes. Cette fois-ci, il ne peut pas être remplacé par deux droites croisées (mais bien par 8). Les orientations des traces du dièdre peuvent être changées de 45o ; elles deviennent NO-SE, NE-SO, et les papiers originaux doivent aloprs être des triangles. Figs 7 et 8.

 

 

Fig. 7 Deux miroirs NS et OE croisés en signe +, 4 strates superposées. Image 12.jaune.

 

 

Fig. 8. Deux miroirs NO SE et SO NE croisés en X, 4 strates superposées. L’original comporte 4 triangles papiers. Image 17.jaune.

L’opération miroir agissant sur les cases coupées en moitiés triangulaires en préparant l’original ne fait pas apparaître de cases nouvelles. Elle les complète.

 

La figure se prête donc à 2 opérations de symétrie double miroir chacune, de même axe dièdre, à 45o l’une de l’autre, l’une en forme de signe + (Fig. 7), l’autre de X (Fig. 8). Réf. 2. Il y a ainsi un quadruple miroir. Le quadruple miroir s’applique évidemment à chaque strate isolée.

 

4a. Enfin le tableau en quart d’ellipse. Il ne possèderait aucun miroir utile de son ensemble, les miroirs tels que ceux ci-dessus n’affichant aucune nouveauté parce que tous les miroirs possibles sont inscrits dans ce tableau par groupes de 4 éléments formant des tétrades, une tétrade par grande case. Il suit que chacune de ces grandes cases est d’avance pourvue de 4 miroirs, aussi bien que la strate 1 de 3 ci-dessus, soit 120 au total.

4b. Le caractère composite de ses grandes cases confère au présent tableau une propriété nouvelle qu’on peut décrire comme une aptitude à un encryptage suivi d’un désencryptage par symétrie miroir. Les 4 opérations miroirs principales pratiquées sur le tableau amènent tour à tour chacun des 4 éléments de chaque tétrade à occuper chacune des quadrants, disons la position NO, appelée principale en héraldique. Cette lecture est facilitée par les retournements des écritures dans chaque grande case : GD, DG, HB, tête–bêche, i.e. retourné de 180o dans son plan. Convenons de ne lire que les noms visibles dans ce quadrant, le double miroir agit dès lors comme un révélateur ou un décodeur du tableau elliptique encrypté dans le tableau quart-d’ellipse. On ne lit que les noms lisibles. Le tableau est devenu un tableau quart d’ellipse encrypté ou codé.

Image 26 jaune

Image 27 jaune.

Fig. 9. Tableau quart d’ellipse codé, miroirs dièdres, 2 mises au point.

 

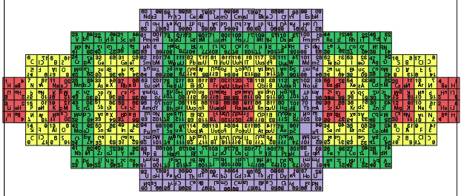
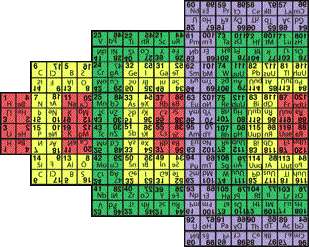
Fig. 9. Tableau quart d’ellipse codé et ses retournements principaux. On trouve 120 cases lisibles. 480cases, moitié1, moitié2 de 1 jaune

 

quadMsuppl

 

 

 

Enfin, le tableau quart d’ellipse codé en 4 strates.

La figure 9 peut être reprise en séparant les strates et en les superposant, aussi bien que dans la figure 7. On aperçoit le jeu du codage et sa solution par les symétries miroirs. Fig. 11.

Fig. 11. Photo avec miroirs dièdres du tableau quart d’ellipse codé en 4 strates. Certaines parties de l’image en cachent d’autres. Tous4.jpg

 

En photographiant les strates une à une, on voit mieux l’effet des miroirs sur toute leur étendue. Fig. 12abcd

 

a

b

c

d

Fig. 12. Comme Fig. 11, les strates séparées. Bleu4.jpg, Vert4.jpg, Jaune.jpg, Rouge4.jpg

 

Et voici les effets des miroirs simulés par modélisation 3D. Fig. 13

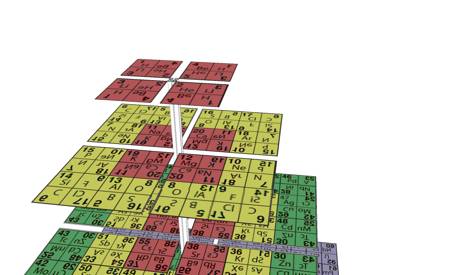
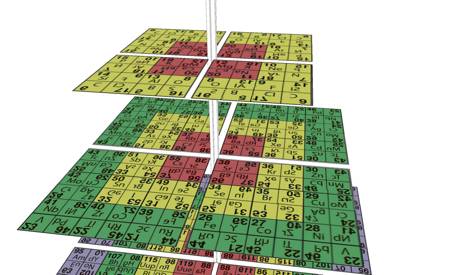
Fig. 13. Comme Fig. 11, obtenu à partir du modèle 3D. Trois points de vue fixés, montrant le détail des miroirs des 4 strates. QuatreMiroir12.png, QuatreMiroir234.png, QuatreMiroir34.png

Vous trouverez le modèle 3D à l’adresse suivante :QuatreMiroir

 

2D ou 3D? Relativités.

Examinons les effets miroirs à l’aide du plan Fig. 3. Un papier, soit une image sur papier plan est naturellement 2D. Son image par réflexion simple dans un miroir placé à angle droit symbolise une rotation de 180o autour de la droite du dièdre papier-miroir. Cette opération miroir implique donc une 3^e dimension, elle ne peut pas se comprendre dans 2 dimensions seulement.

L’effet obtenu par une double réflexion dans un dièdre de miroirs pourrait être remplacé par une rotation de 180o dans le plan de l’objet original et cela ne requiert pas une 3^e dimension.

Toute rotation s’accompagne d’une accélération et l’interprétation correcte des accélérations comme des forces requiert la relativité généralisée. Cela est satisfaisant puisqu’on sait que le spin de l’électron doit s’interpréter en relativité généralisée. Or le miroir horizontal càd le passage d’un quadrant O à un quadrant E change un moment cinétique qui est le spin. Et cela suggère que le miroir vertical càd le passage d’un quadrant N à un quadrant S lui aussi concernerait un moment cinétique qui n’est pas le spin.

 

Dans un cristal, le passage d’une maille à une autre s’effectue sans rotation et par pure translation.

 

Références.

Réf. 1. Pierre Demers 2010, Système du Québécium.  Le tableau périodique de Mendéléev est un double miroir. 7 et 8 III2010 Traduction interdite.

http://er.uqam.ca /nobel/c3410/DoumiroirTDEL.htm

 

Réf. 2. Auteur ? Blasons. L'héraldique et l'art des blasons, http:// blasons.free.fr/heraldique/herald.html - hrd_def

Ce site présente des appellations de l’héraldique, « Le partitionnement est le premier découpage physique de base d'un écu. » Le partitionnement en croix latine selon le signe + est appelé l’écartelé; en croix de Saint-André selon le signe X, l’écartelé en sautoir. Ces partitionnements déterminent des quartiers au sens de la géométrie, soit découpage en 4. Le canton NO visible en haut à gauche est appelé dextre du chef parce qu‘il se trouvait à la droite du chevalier qui portait l’écu au bras gauche.

-30-