Sbiom2002SolQc. html

21 juillet 2002

Communication proposée au XVIIIe colloque de Biomathématique, Versailles, 19-20 septembre 2002

Chacun des 5 solides réguliers de Platon SP présente des éléments géométriques tous égaux : faces, arêtes, angles plans, dièdres et solides; il s'inscrit dans un cube. On propose de créer une nouvelle classe de solides contenant en outre, le rhombododécaèdre RD, qui possède plusieurs éléments de régularité : faces toutes égales (losanges), arêtes toutes égales, angles dièdres tous égaux, inscription dans un cube. Il attire l'attention par son rôle dans le système du Québécium 3D et par sa propriété de paver l'espace, seul le cube parmi les SP possède cette propriété. Le RD se construit en enlevant 6 arêtes au dodécaèdre des SP : voilà 2 figures isoédriques, ce qui suggère une avenue pour résoudre l'énigme des cristaux pentagonaux. Le RD se construit aussi à partir du format de papier A4, lequel contient un losange inscrit dont les axes ont le rapport voulu : racine carrée de 2. Figure : losange A4 21 X 29,7 cm. La nouvelle classe renferme 6 solides et seulement 6. Le nombre 6 = 2X3 peut paraître plus satisfaisant que le nombre 5. On peut dire solides homoédriques, signifiant faces égales, ou solides de Québec, en l'honneur de l'Université Laval site du 70e congrès de l'ACFAS et du célèbre Pont de Québec.

Figure. Les étapes, du losange A4 au rhombododécaèdre. RD construit à partir de papier A4.

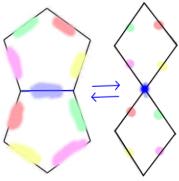
Figure. Enlèvement ou addition d'une arête, une face pentagone devenant losange et réciproquement

(Cette communication était primitivement destinée au 70e Congrès de l'ACFAS mais n'est pas parvenue à temps).

"Solide comme le Pont de Québec", rappel historico-géographique, appellation suivant la manière des solides de Platon.

Merci à Jacques Costagliola qui m'a appris le principe du format A4.