SSVolCompl1bis

26 avril 2008

http://www.lisulf.quebec/quebecium.html

Système du Québécium

Solides sans volume. Compléments.1

Pierre Demers

Traduction interdite

 

Résumé. J'ai montré précédemment qu'un processus de dérivation que j'appelle ici jonction, appliqué à certains solides réguliers, analogue à celui qui produit les solides coiffés, permet d'obtenir des solides n'enfermant aucun volume. À partir des 11 solides réguliers que j'admets, j'ai ainsi produit 4 solides sans volume. Ils se divisent en 2 catégories, le tétraèdre sans volume se distinguant des 3 autres parce que les surfaces qui le composent ont obligatoirement une seule face. Pour des raisons conceptuelles, je réservais le cas des 7 solides restants parce qu'ils seraient composés de surfaces ayant une seule face sur une partie seulement de leur étendue. Je crois maintenant  que cette objection n'est pas valable. Je présente donc la possibilité de 7 solides réguliers sans volume nouveaux, avec des figures représentant la jonction de 3 de certains d'entre eux : octaèdre sans volume, dodécaèdre sans volume, icosaèdre sans volume. Somme toute : il existe 11 solides réguliers sans volume, en plus des 11 solides réguliers normaux. Au total, il existe 22 solides réguliers.

 

Introduction.

Je rappelle ce que j'écrivais dans mon travail précédent:

http://www.er.uqam.ca/nobel/c3410/QbSansvXI2007bis.htm

Dans le cas de l'octaèdre, du dodécaèdre et de l'icosaèdre réguliers, j'ai pu croire que le processus serait applicable, puisque les faces viennent 2 par 2 vis-à-vis opposées parallèles et de formes planes semblables. Cependant, il me paraît maintenant sans intérêt parce que les faces opposées ne coïncident pas par une pure translation. La translation seule suffit pous amener à confondre 2 faces vis-à-vis dans un plan unique, mais à ce moment, leurs formes sont décalées. Pour amener en coïncidence leurs formes, il faudrait ajouter une rotation : 2π/6 pour l'octaèdre et l'icosaèdre, 2π/10 pour le dodécaèdre. Or, dans un souci de préservation des symétries choisies, j'exclus les rotations

(Le souligné est actuel).

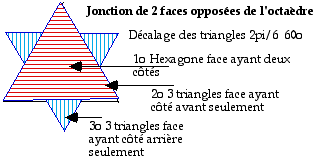
Fig. 1. Jonction de 2 faces opposées de l'octaèdre.

 

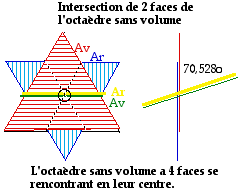
Fig. 2. L'octaèdre sans volume, plan.

 

J'ai changé d'opinion. Le processus peut fort bien se suffire, de translation sans rotation. Deux faces opposées de l'octaèdre opèrent une jonction, elles viennent se joindre dans un plan unique et le décalage angulaire de 2π/6 détermine 7 régions de 3  types : 1o un hexagone où la surface a 2 côtés; 2o 3 petits triangles n'ayant que le côté avant; 3o  3 petits triangles n'ayant que le côté arrière. Fig. 1. Comme dans le cas du tétraèdre, le processus fait apparaître des surfaces n'ayant qu'un côté. Fig. 1.

Je donne le plan de l'octaèdre sans volume. Fig. 2.

Dans le cas du tétraèdre, il n'y a pas jonction, le processus de translation se termine avec l'apparition d'une face du type 2o. Fig. 3.

Fig. 3. Ptocessus pour une face du tétraèdre.

 

Jonction. Pour la commodité, j'appelle ici jonction le terme du processus de translation qui donne lieu à la disparition du volume enfermé dans un solide régulier, et qui est particulièrement facile à comprendre dans le cas du cube. Fig. 4.

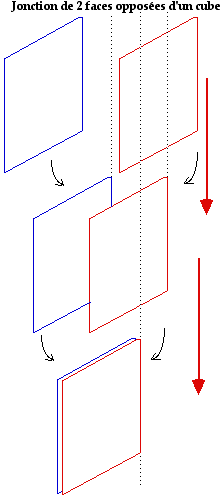
Fig. 4. Translation et jonction. Deux faces d'un cube.

 

Dans le cas du cube, il y a jonction de 2 faces opposées et formation d'un carré ayant 2 côtés, avant et arrière. Figs 5, 6

Fig. 5. Jonction de 2 faces opposées du cube.

 

Fig. 6. Le cube sans volume, plan.

 

Dans l'icosaèdre, les faces vis-à-vis sont des triangles orientés mutuelement comme dans l'octaèdre; son cas est donc semblable à celui de l'octaèdre. Fig. 7.

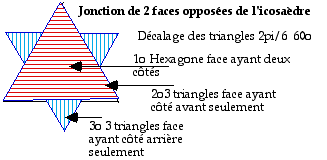
Fig. 7 Jonction de 2 faces opposées de l'icosaèdre.

 

Le cas du dodécaèdre est comparable à celui de l'octaèdre les faces vis-à-vis sont décalées, cette fois de 2π/10. Il y a un décagone à 2 côtés et 10 triangles n'ayant qu'un côté. Fig. 8.

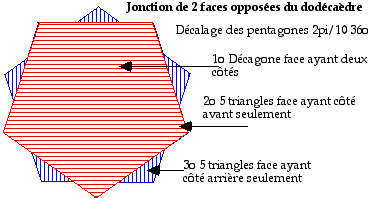
Fig. 8. Jonction de 2 faces opposées du dodécsaèdre.

 

Voilà donc pour les 5 solides de Platon. Le cas du rhombodod.caèdre régulier est comparable à celui du cube. Les faces vis-à-vis se superposent sans décalage. Fig. 9.

Fig. 9  Jonction de 2 faces opposées du rhombododécaèdre sans volume.

 

Et voilà le cas du rhombodod.caèdre régulier étoilé. Les faces vis-à-vis se superposent sans décalage. Fig. 10.

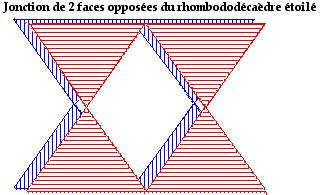
Fig. 10. Jonction de 2 faces opposées du rhombododécaèdre étoilé sans volume. Chaque face est en 4 parties..

 

Conclusion. Les 22 solides réguliers.

Quant aux 11 solides sans volume. J'ai représenté 4 d'entre eux dans la référence.

•Tétraèdre régulier sans volume 12

•Cube sans volume 13

•Rhombododécaèdre régulier sans volume 17

•Rhombododécaèdre régulier étoilé sans volume 18

Je montre ci-dessus le commencement d'une représentation pour 3 autres.

•Octaèdre régulier sans volume 14

•Dodécaèdre régulier sans volume 15

•Icosaèdre régulier sans volume 16

Quatre restent auxquels je n'ai donné aucune illustration.

• Petit dodécaèdre étoilé sans volume

• Grand dodécaèdre étoilé sans volume

• Grand dodécaèdre sans volume

• Grand icosaèdre sans volume

 

Liste.des 22 solides réguliers, y compris 11 sans volume.

 

1. Tétraèdre régulier

2. Hexaèdre régulier ou cube

3. Octaèdre régulier

4. Dodécaèdre régulier

5. Icosaèdre régulier

6. Rhombododécaèdre régulier

7. Rhombododécaèdre régulier étoilé

8. Petit dodécaèdre étoilé.

9. Grand dodécaèdre étoilé

10. Grand dodécaèdre

11. Grand icosaèdre

Solides sans volume, Nos 12 à 22.

12. Tétraèdre régulier sans volume Fig. 4 (Fig. 1, 1 bis)*

13. Hexaèdre régulier ou cube sans volume Figs 5, 6 (Fig 2, 2 bis)*.

14. Octaèdre régulier sans volume Figs 1, 2

15. Dodécaèdre régulier sans volume Fig. 8

16. Icosaèdre régulier sans volume Fig. 7

17. Rhombododécaèdre régulier sans volume Fig. 9 (Figs 3, 3bis)*

18. Rhombododécaèdre régulier étoilé sans volume Fig. 10 (Figs 4, 5)*

19. Petit dodécaèdre étoilé sans volume

20. Grand dodécaèdre étoilé sans volume

21. Grand dodécaèdre sans volume

22. Grand icosaèdre sans volume

 

NB. Étoilé = coiffé.

 

*Référence :

http://www.er.uqam.ca/nobel/c3410/QbSansvXI2007bis.htm

-30-