SSVolCompl2ncell
http://www.lisulf.quebec/quebecium.htm
Systme du Qubcium
Solides sans volume.
Les hexadres. Le nombre de
cellules.
Rgles gnrales.
Pierre Demers et Patrick Demers
Traduction interdite
18X-7XII2010
Rsum. LĠun de nous a montr prcdemment
qu'un processus de drivation comprenant translation et jonction, appliqu
certains solides rguliers, en quelque sorte orthonormal celui qui produit
les solides coiffs, permet d'obtenir des solides n'enfermant aucun volume, qui
sont des polydres non ferms, et
des semi-surfaces, qui sont des
surfaces nĠayant quĠun ct. Ont t ainsi dcrits quelques uns des
solides sans volume possibles, avec photos de modles 3D et figures
manipulables. Rf 1, 2. Nous poursuivons ici leur tude, en envisageant cette
fois les hexadres et le nombre de cellules rsultantes. Ce nombre est gal ou
suprieur au nombre de sommets du solide original. Nous nonons des rgles sur
le nombre des cellules polydres ouverts obtenus et sur le nombre de leurs parois.
Nous recourons la reprsentation
des parois par leur horizon, figur par un point sur une sphre. Nous considrons le cas des solides non rguliers sans volume. Nous
prsentons des modlisations 3D manipulables et des animations 2D, obtenues
avec le logiciel Sketchup.
Introduction.
Nous
prsentons successivement plusieurs types dĠhexadres avec nos commentaires et
nous terminons en nonant des rgles gnrales concernant les solides sans
volume.
Hexadres 1. Le Cube.
Le
cube est un solide rgulier et de Platon, le plus simple des hexadres, solides
limits de routes parts par des parois planes. Rappelons un travail prcdent,
qui prsentait les solides sans volume. Rf.1
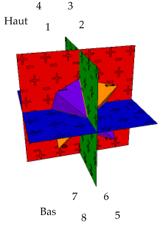
Voici un cube et un cube sans
volume, papier lĠun et lĠautre. Les 6 parois opposes 2 2 du cube sont
rapproches virtuellement, ce qui est la translation et se rejoignent en
formant 3 surfaces tridres se croisant au centre de figure. La translation
amne le centre de figure dĠune paroi concider avec le centre de gravit du
solide. Fig. 1.
a b
b
 c
c
Fig. 1. a Un cube papier.
Cubepap.png
b Le mme devenu cube sans volume
avec couleurs RVB. CubePapSv.png
c Idem sans couleur. CubeSvScou.png
Jonction.
Nous appelons jonction le terme du
processus de translation, qui donne lieu la disparition du volume enferm
dans un solide, particulirement facile comprendre et dcrire dans le cas
du cube, cause de lĠorthogonalit mutuelle des parois opposes prises 2 2.
Fig. 2.
En
principe, nos vues fixes sont en perspective oblique. Les orientations
principales des plans sont colores RVB aussi bien que les axes xyz
trirectangles qui leur respectivement perpendiculaires. Un axe est donc muni de
la couleur de la paroi qui lui est perpendiculaire. Le plan V fait face
lĠobservateur. La face la plus proche de lĠobservateur est munie du signe +,
son oppose parallle, du signe –.
Nous
appelons parois les portions de surfaces planes limitant un solide.
a  b
b  c
c 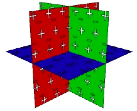 .
.
Fig. 2. Translation et jonction du cube.
a Un cube aux 3 couleurs RVB.
b. En animation. Translation des
parois R+ et R-, annulant le volume la jonction.
Animation.CubeGIF.gif
c Aprs jonction le cube sans volume
Dans
le cas du cube Fig, 1a, il y a jonction de 2 parois opposes sĠajustant
exactement lĠune lĠautre avec formation d'un carr ayant 2 faces, + avant et
- arrire. Voici le rsultat isol pour les 2 parois V. Fig. 3. Et la vue en
plan du rsultat pour les 3 parois la jonction. Fig. 4
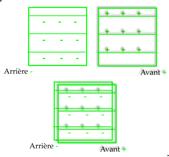
Fig. 3. Jonction de 2 parois V opposes + et -, contenant les axes x et
z. CubeAvArV.png

Fig. 4. Le cube sans volume, plan B contenant les parois + et -, lĠaxe
z est en bleu. Les carrs R et V apparaissent par leurs traces en pointill.
CubePlanB.png
Horizons.
Nous recourons la reprsentation des parois
par leur horizon, figur par un point sur une sphre, la sphre des horizons
assimilable la sphre des angles solides ou la sphre cleste augmente de
sa rplique vers le bas. LĠhorizon autour de chacun est caractris par une
verticale oriente znith – nadir qui perce la sphre cleste mesurant
2pi, celle dĠun observateur voyageur spatial quelque distance de la terre
mesurant 4pi. Voil cetytye sphre rersente. Fig. 4bis.
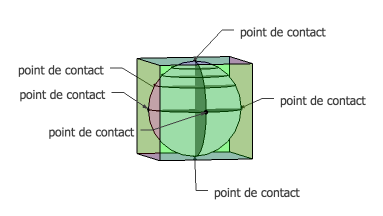
Fig. 4bis. Ls sphre des horizons. Les cercles
concentriques marquent les latitudes lĠquateur 0o, 30o, 45o, 60o, les ples
90o. Les 6 points de contacts avec le cube inscrit ou points principaux.
Sphere1X.png
Imaginons une perpendiculaire porte au centre
de chaque paroi dĠun solide, elle ou sa parallle passant par le centre de la
sphre perce cette sphre ou sa reprsentation en un point que nous marquons
par une pastille. Les parois dĠun solide contenant les axes x et y apparaissent
par une pastille au sommet de la sphre ou znith pour la face suprieure + et
une autre sa base ou nadir pour la face infrieure –, qui sont donc
superposs dans une reprsentation 2D en plan de la sphre. Pastille noire =
point figuratif au dessus du plan du papier; pastille blanche, en dessous de ce
plan. Le canevas Fig. 5. Par exemple, la surface dĠun lac servant de paroi
suprieure dĠun cube: les lacs S. Pierre et S. Louis, peu loigns lĠun de
lĠautre gographiquement ont le mme horizon, soit le mme znith, pastille
noire unique sur le canevas plan B ci-dessous.
Cette reprsentation a la particularit dĠtre
prserve quand un solide normal devient sans volume puisque lors de la
translation, une paroi se dplace paralllement elle-mme. Elle est la mme
pour tous les plans parallles et ne dpend pas de la forme de la surface
occupe ni de son extension.
La sphre des horizons peut se reprsenter par
un canevas contenant les 3 projections plan, lvation, profil. Fig. 5.
Pour chaque paroi du solide considr, on y inscrira les pastilles
descriptives.
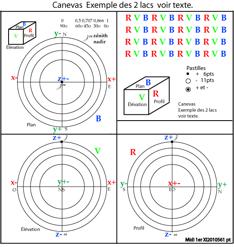
Fig. 5. La sphre des horizons. Canevas,
ses 3 vues trirectangles plan, lvation, profil. Dans le cube, toute surface
est paire cd lui correspond une autre qui lui est parallle, la plus proche
de lĠobservateur portera le signe +, lĠautre, le signe -. Des parois paires +
et – sont lies znith et nadir, mutuellement antipodes. Dans le cas
gnral, si une paroi est non paire, on lui attribuera le signe +. CanevasMidi1erXI2010.png
Ë lĠusage, une seule de 3
projections planes de ce canevas nous a paru suffire, celle en plan, les 2
autres rptant lĠinformation. Le canevas ainsi simplifi parat Fig. 5bis
Canevas Plan. LĠquivalent est de plus prsent en version 3D et 2D de 3D
a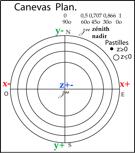 bcËvenir
bcËvenir
Fig. 5bis. Le Canevas Plan de la
sphre des horizons. a Version
dessin. CanevasPlan9XI2010.png b Version 3D. c Version 2D de 3D
Le
Cube dcrit en terme dĠHorizons.
Voici lĠapplication du canevas des
horizons la description du cube. Fig. 6. Les 6 points principaux de la sphre
rpondent aux 6 parois limitant le cube.
a b
b
Fig. 6. Horizons du cube et de la poutre, tous hexadres ayant tous
angles droits, sur le Canevas Plandes horizons o les 6 parois apparaissent
comme 5 pastilles dans chaque projection plane : 6 points pour 6 parois, 2
points confondus pour les parois vues de face. CanevasPlanCube9XI2010.png
Voici
pour illustrer et mieux comprendre les tapes et les espaces gomtriques au
cours de la translation. Ë son dbut, 6 parois sont en jeu, elles se dplacent.
Fig. 7.
a 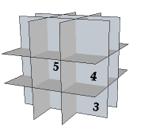 b
b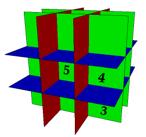
Fig. 7. Nombre de parois des cellules. a Un cube non color en cours de
translation. XXX
b Un cube color RVB en cours de translation. Vue obtenue avec le
logiciel sketchup. Six parois sont en dplacement. On reconnat 3*9 = 27
espaces dfinis par au moins 3 parois. Les espaces nouveaux sont de 3 types,
limits par 3, 4 ou 5 parois. Rendu 2D dĠun document sketchup. CubeContr1.
Png Certaines de nos figures requirent la possession et
lĠusage du logiciel sketchup. Annexe 1.
Les
27 espaces (cube).
Nombre
des espaces, les nouveaux et le rsiduel, prsents au cours de la translation
du cube. Le type dĠespace est caractris par le nombre de parois le limitant,
au moins 3.
Espaces
nouveaux
ayant
3 parois: 8; (persistent dans le rsultat la jonction) ;
ayant
4 parois: 12; (disparaissent dans le rsultat la jonction) ;
ayant
5 parois : 6 ; (disparaissent dans le rsultat la jonction) ;.
Espace
rsiduel central
Ayant
6 parois : 1 (seul au dbut, disparat la jonction) ;
Total
27.
Parmi
les 27 espaces, 26 sont donc nouveaux et ouverts, le rsiduel central ou cube
central tant un espace ferm, 8 persistent formant des octants.
Une
fois la jonction ralise, les 6 parois + et - se sont unies 2 2 pour former
les 3 plans Fig. 4, et le cube central finalement nĠoccupe plus quĠun espace
ponctuel. Au dbut du processus de translation, apparat chaque sommet du
cube un espace limit par 3 portions de plan, soit 8 tels espaces qui, en fin
de processus persistent seuls. Ce sont des octants, dĠangle solide pi/2.
Pour
le cube gris non color, les espaces 3 sont tous congruents entre eux, il en
est de mme des 6 espaces 5 et des 8 espaces 4.
Pour
le cube color, les 8 espaces 3 sont congruents entre eux par groupes de 4,
aussi bien pendant la translation que dans le rsultat la jonction. Voyez ce
rsultat plus bas. Les espaces 4 sont congruents entre eux, il en est de mme
des espaces 5.
Vues 3D manipulables.
Le
logiciel skp permet de prsenter une vue 3D manipulable de Fig. 7.
Si le modle 3D, ci-dessus, n'apparait pas veuillez cliquer sur ce lien. Cube2DContr2C.pdf
Congruences. Chiralits.
Le
cube sans volume non color Fig. 7a prsente 8 cellules trirectangles toutes
congruentes entre elles. Cette congruence rclame un prix payer, soit des
dplacements et retournements comprenant des translations et des rotations dĠun
droit ou plus dĠun, selon un axe ou plus.
Il
en est pareillement pour le cube sans volume color 2 couleurs RVV, si on
ignore des diffrences possibles de prix payer.
Il
en est autrement pour le cube sans volume color 3 couleurs RVB. Avec un prix
payer, et avec la numrotation choisie, les 4 cellules impaires 1, 3, 5, 7 sont
congruentes entre elles et les 4 cellules paires 2, 4, 6, 8 sont congruentes
entre elles. Il nĠy a pas de congruences entre cellules paires et impaires. Si
on remplace chaque cellule par un point centr, les 8 points sont aux 8 sommets
dĠun cube , chaque point est reli ses 3 voisins de mme parit selon les
petites diagonales de ce cube. Le rsultat est la dfinition de 2 ttradres
rguliers dont les artes se rencontrent selon des droits. Fig. 9.
Ces observations peuvent se prsenter en termes
de chiralits ou dĠnantiomorphismes, ralits et notions importantes en
strochimie, en thorie de la vie et en mdecine: problmes des gauchers,
dyslexie et apprentissage.
Rappelons que dans tout cube, on peut tracer
des petites diagonales en travers des parois, et que ces 12 segments de droites
dessinent 2 ttradres inscrits aux artes croises. Ce sont des ttradres de
Platon.
Si le modle 3D, ci-dessus, n'apparait pas veuillez cliquer sur ce lien. CubeCont4Tetra.pdf
Fig. 9. Montre les 8 points centrs et les 2 ttradres quĠils
dterminent
a On reconnat 8 octants
du cube sans volume, organiss en 2 systmes de 4 cellules congruentes. Ces
systmes sont marqus par les petites diagonales qui dessinent 2 ttradres rguliers
aux artes croises angles droits, sur les faces dĠun cube virtuel de ct
gal lĠarte dĠun octant. CubeTetra6XI2010.png
Les sommets visibles sont successivement violet 1 et orang 2 en haut,
orang 8 et violet 5 en bas
b CĠest la figure a manipulable 3D avec des numros aux sommets
Les miroirs.
Le cube sans volume possde 3 miroirs de symtrie trirectangles se
croisant lĠorigine. Dans lĠencoignure dĠun tridre de miroirs plans en plexi,
plaons le tridre papier de lĠoctant suprieur droit avant. Il apparat
multipli en 8 exemplaires assembls correctement comme dans la figure en 8
octants papier. Chaque rflexion introduit un facteur 2 dans le nombre
dĠimages. Cela est vrai pour le cube sans couleurs et pour les cubes colors
RVV et RVB.
a b
b 
Fig. 10. Miroirs trirectangles plexi multipliant
par 8 lĠoctant papier du cube sans volume.
a Avec une seule couleur.
Image3miroirs3h531X2010.png
b Couleurs RVB. Image3Miroirs3Coul.png
Surfaces nĠayant quĠun seul ct. Les
semi-plans. Les semi-surfaces.
Le rsultat de la jonction est une
collection de surfaces, chacune ayant 2 faces, avant + et arrire -, chacune de
ces faces provenant dĠune paroi originale du cube. Puisque la jonction des 2 parois
produit une surface 2 cts, il est logique dĠattribuer un ct et un seul,
chacune des parois avant leur jonction. Nous arrivons ainsi au concept dĠune
face plane ou paroi, limite dĠun espace 3D, nĠayant quĠun ct, concept signal
dans Rf. 1, sous lĠappellation anti-Mbius. Ce concept pourra tre discut
davantage dans une publication distincte. Dans les figures prsentes ici, il
sĠapplique toutes les parois limitant le cube ou lĠhexadre initial et ce
quĠil en reste en fin de translation. Dans les diagrammes des horizons XXFigs
4b et 8b, chacun des points marquant 2 2 une paroi dsigne un demi-plan
orient vers lĠextrieur.
On pourrait gnraliser. Toute paroi
limitant un volume est un demi-plan, nĠayant quĠun ct, si ce volume
est celui dĠun solide. LĠappellation demi-plan a son mrite, mais afin
dĠenglober le cas de surfaces non planes, une appellation gnrale serait demi-surface.
Il faudrait examiner lĠanalogie
physique et biologique avec les lames de savon dans les bulles de savon, les
membranes des cellules vivantes, la couche de glatine enveloppant les cristaux
de bromure dĠargent dans les mulsions photographiques et ionographiques au
glatino-bromure dĠargent.
Kauffman Rf. 3 a tudi longuement
les nÏuds et le cas du ruban de Mbius, dont les deux faces, dveloppes en 3D,
semblent nĠen former quĠune par continuit.
Hexadres 2. La Poutre.
Le
cube, solide rgulier et de Platon, appartient une immense famille, celle des
hexadres et plus prcisment, des hexadres trirectangles, dĠintrt
pratique bien connu en commerce et en architecture. Dans ces derniers, tous les
angles didres et ceux entre artes aux sommets sont des droits et les parois
sont des rectangles 2 2 opposs et parallles. Ils mritent le nom de poutres,
les artes tant de 3 longueurs en gnral ingales choisies ici comme tant
123. Il nĠapparat pas de raison qui interdirait dĠappliquer aux poutres les
oprations de translation et de jonction dcrites pour le cube. Fig. 2.
Une
poutre peut subir une translation et devenir une poutre sans volume. Comme
lĠhorizon dĠune paroi ne dpend que de lĠorientation de la perpendiculaire
ses dimensions latrales, il est insensible ces dernires et. rciproquement,
lĠinspection du canevas ne nous renseigne pas sur les dimensions des parois, ni
dĠailleurs sur leur forme. Par suite, les figures ci-dessus pour le cube se
rptent avec ajustements pour la diversit des longueurs des axes, pour la
poutre sans volume et pour la poutre. Fig. 6. Rptons que lĠinspection de la
sphre et du canevas des horizons ne renseigne ni sur les longueurs des artes,
ni sur le volume enferm dans le solide original.
a
bc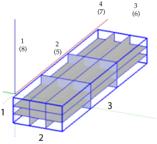
 d
d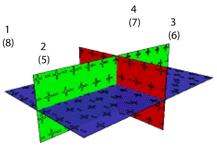
Fig. 11. Une poutre 123. a Papier normale et sans volume sans volume
image clate. LĠoctant papier est multipli par 8 dans un tridre de miroirs
plexi. Eclatee.png
b Une poutre grise et ses 3 artes ingales 123 une tape de sa
translation. Les petits chiffres sont les numros assigns aux 8 cellules
sommitales. PoutreGrise.png
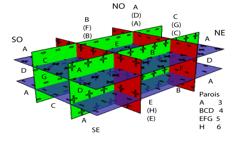
c En couleurs RVB une tape de sa translation. Nombre de parois des
espaces. PoutreEDED.png
d Sans volume. Les parois paires en vis--vis sont + et -. Ce sont des demi-surfaces,
leurs jonctions en forment des surfaces. Cube contracteAsy123-9.gif
Au
cours du processus de translation, aussi bien que pour le cube, 27 espaces
apparaissent. Ë cause des diffrences entre poutre et cube, il y a 3 valeurs
distinctes considrer pour les longueurs des artes. En diffrence dĠavec le
cas du cube, le nombre de parois limitant un espace ne suffit pas
caractriser un type dĠespace. Voici une description.
Ayant
3 parois : 8 = 4A pairs, 4A impairs. Persistent dans le rsultat la
jonction,
Ayant
4 parois: 12 = 4B, 4C, 4D.
Ayant 5 parois: 6 = 2E, 2F, 2G.
Ayant 6 parois: 1 = H. Devient ponctuel la
jonction,
Congruences
et ttradres pour la poutre sans volume.
Ë
la diffrence du cube, la poutre sans volume non colore ou avec 2 couleurs ne
prsente pas 8 cellules trirectangles toutes congruentes entre elles. Colore
ou non, avec la numrotation choisie, les 4 cellules impaires 1, 3, 5, 7 sont
congruentes entre elles et les 4 cellules paires 2, 4, 6, 8 sont congruentes
entre elles. Il nĠy a pas de congruences entre cellules paires et impaires. Si
on remplace chaque cellule par un point centr, les 8 points sont aux 8 sommets
dĠun paralllipde, chacun est reli ses 3 voisins de mme parit selon les
petites diagonales de ce cube. Le rsultat est la dfinition de 2 ttradres dont
les artes se rencontrent selon des angles autres que des droits. Chiralits ou nantiomorphismes sont inhrents
lĠingalit des 3 dimensions de la poutre, que les parois soient colores RVB
ou non.
Ë la ressemblance avec le cube, on peut donc
tracer dans la poutre sans volume 2 ttradres aux artes croises,
correspondant respectivement aux cellules paires et impaires. Mais les
ttradres ne sont pas rguliers et les angles aux croisements ne sont pas des
droits.
Hexadres 3. Faces parallles 2 2.
Le Cube inclin
une fois.
Quatre parois restent des carrs, deux deviennent des
paralllogrammes. Formule 4ca2plg. On dforme le cube, 4 parois B et V restent des carrs
2 2 mutuellement parallles, leurs horizons tant prs de 60o lÔun de
lĠautre. Deux parois R deviennent des paralllogrammes gaux parallles entre
eux. CĠest un prisme base paralllogramme ayant 8 angles didres droits, 2
valant 60o et 2 valant 120o. Figs 12. La reprsentation sur la sphre des
horizons prserve 4 des points principaux B et R comme le cube, 2 points V sont
dplacs. Ici encore, il y a dans la figure sans volume dfinition de 8
cellules tridriques ouvertes et de 2 ttradres inscrits non rgulierscroiss.
a b
b
c
Si le modle 3D, ci-dessus, n'apparait pas veuillez cliquer sur ce lien. CubeInclineXFinalTetra.pdf Fig. 12. Cube inclin une fois a Vue papier. Cube1prlg.png b Comme a, mais plac dans un miroir tridre. On voit que 2 rflexions,
dans un miroir didre, restituent
lĠimage congruente de lĠoriginal. CubePenche1fois.png b Son diagramme en
horizons. CanevasPlanCubeP19XI2010.png c Son aspect 3D manipulable. Tir de CubeinclineX.skp
(HorxCubeInclxx1.ai)
(vxCanevas5h301XI2010.png)
d Image 2D de 3D montrant les ttradres pairs et impairs. CubeInclineFinalTetraC.png Hexadres 4. Le Cube inclin deux
fois. Deux parois restent des carrs, quatre deviennent des
paralllogrammes. On dforme le cube, 2
parois B restent des carrs parallles, 4 deviennent des paralllogrammes
parallles 2 2, les angles didres BR et BV deviennent approxumativement 30o
et 60o dans lĠexemple choisi. CĠest un prisme base carre sans aucun angle
didre droit a Fig. 13. Cube inclin 2 fois. a Vue Papier. Cube2Prlgr2XI2010.png
b Son diagramme en horizons CanevasPlCubeI2fois.png c Ë une tape de sa translation.
LĠhexadre
Fig. 13a devenu sans volume. Trois surfaces planes entirement +- se croisent
lĠorigine, lĠune est un carr, les deux autres sont des paralllogrammes.
Elles dterminent 8 cellules
octants, chacune tant une vue partielle de Fig. 13a avec rduction ½ en
diamtre. Les parois de ces octants sont +-, tous les angles didres sont des
obliques. On peut y inscrire 2 ttradres non rguliers comme dans le cas du
cube inclin 1 fois Fig. 12d, mais avec des angles diffrents. Les cellules de
lĠhexadre inclin deux fois sans volume sont des
octants eux aussi inclins par rapport ceux du cube. Ils
en diffrent par lĠapparition dĠangles didres obliques, ils sont au nombre de
8 et sont formes de surfaces normales ayant 2 cts. Les 4 hexadres sans
volume tudis jusquĠici (1 4)
se composent de 8 cellules tridriques. Pour le cube et la poutre, ces
cellules sont toutes trirectangles, il en est autrement pour le cube inclin une fois ou deux fois. Hexadres 5. Le Cube inclin quatre
fois. La pyramide tronque. Deux parois sont des
carrs parallles mais ingaux + au haut de la figure, - en bas servant de
base, la distance entre ces carrs est la hauteur ; 4 parois latrales
sont des trapzes gaux entre eux +. CĠest une pyramide quadrangulaire
tronque. La translation sĠopre vers le centre de gravit du solide dfini, la
jonction sĠeffectue quand le centre de figure de chaque paroi a t amen au
centre de gravit. Ce cdg est situ sur lĠaxe de symtrie B une hauteur au
dessus de la base gale 76/39 =1,95, soit sensiblement mi-hauteur. a d Fig. 14. a Un hexadre driv du cube modifi devenu pyramide quadrangulaire
tronque, ayant 2 parois carrs
parallles ingaux et 4 parois trapzes gaux, dont 2 seulement sont figures,
formant avec les carrs des angles didres 90-36,9 = 53,13o et 36,9+90 =
126,87o, soit sensiblement la moyenne entre 30o et 45o ou entre 60o et 45o. b Son diagramme en horizons. CanevasPlanPyrTr539XI2010.ai c Son image 2D de 3D comme a et b (mais angles didres autres). d et e Comme c, des tapes successives de la translation. f Comme c, mais aprs jonction.
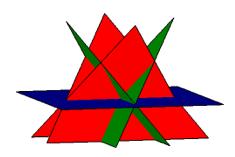
CĠest la pyramide tronque sans volume. Elle montre 18 cellules non
femes: 2 sont ttradres et 16 sont tridres. Les parois sont des semi-parois
sauf une portion infrieure B. PyramTronSVol.png Quant aux congruences entre cellules Fig. 14, il nĠy en pas
entre celles au dessus et celles en dessous de la paroi B. Dans lĠespace
suprieur, les 4 cellules tridriques R2V sont congruentes entre elles et il en
est de mme des 4 cellules RVB diamtralement opposes ; le mme nonc
sĠapplique six cellules de lĠespcae infrieur. Les 2 cellules 2V2R nĠont pas de
congruences. Hexadres 6. Le Cube inclin quatre
fois. La Pyramide quadrangulaire. La face suprieure de la
pyramide tronque qui prcde est rduite la limite un point et nous avons
une pyramide quadrangulaire, rgulire si les faces sont comme ici choisies
triangles quilatraux. Nous lĠenvisageons comme un hexadre modifi. Elle est en fait un
pentadre 4 faces triangles quilatraux gaux, soit une moiti dĠoctadre
rgulier. LĠoctadre rgulier est un solide rgulier et de Platon. Si son arte
vaut lĠunit, sa hauteur vaut racine carre de 2 = 1,4142. La hauteur de la
pyramide est 0,7071, La pyramide
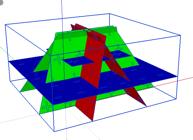
quadrangulaire aussi se prte devenir sans volume. a Fig. 15. Une pyramide quadrangulaire
moiti dĠun octadre rgulier. a Un modle papier. b Son image 3d
.skp. c Son image 2D de 3D.
Tir de .skp. d La description plus haut pour la pyramide tronque reste
valable pour la pyramide sans troncature, congruences comprises, sauf lĠabsence
de toute surface ayant 2 cts dans la pyramide sans troncature.
Observations. 1. La translation. La translation rpond un protocole, consistant
dplacer une paroi du solide original paralllement lui-mme jusquĠ ce que
son centre de figure concide avec un point choisi comme centre de figure du
solide sans volume. Le choix de ce point est arbitraire, il peut tre le centre
de gravit du solide original, mais il doit tre le mme pour la translation de
chacune de ses parois. Ce protocole est appliqu chacune des parois du
solide original. 2. Rgles sur le nombre des
cellules dans les hexadres prcdents. Voici un recensement des
rsultats du prsent travail pour le cas des 6 solides sans volume prsents,
tous des hexadres. Ils se classent en 2 sous-catgories. 1o. Solides sans
volume de 1re catgorie, Nos 1 4 ci-dessus. Cube, poutre et autres
solides hexadres ayant 2 parois carrs parallles et des parois quadrilatres
celles-ci gales et opposes parallles 2 2, inclines ou non. Il y a dans le solide
sans volume : 8 cellules tridriques.
Chacune provient dĠun sommet du solide original. Il y a autant de cellules que
de sommets dans le solide original. Total 8 cellules. 2o. Solides sans volume
de 2e catgorie, Nos 5 et 6 ci-dessus. Les hexadres normaux ont 2 faces
opposes parallles horizontales, dont lĠune est la base et lĠautre peut tre
rduite un point. Les 4 faces latrales sont non parallles : i.
e., aucune dĠentre elles nĠest parallle une autre. Le solide sans volume
est form de 6 semi surfaces dont 2 sont runies partiellement en une surface
ou de 5 semi-surfaces et dĠun point Il y a 8 cellules
tridriques au-dessus du plan central, dont 4 provenant des sommets tridres du
solide original. Il y a 8 autres cellules
cellules tridriques en-dessous du plan central, dont 4 provenant des sommets
tridres du solide original et 8 autres. Soit 16 cellules
tridriques. Il y a en plus 2
cellules ttradriques. Total 18 cellules. Conclusions. 1. Il reste contrler
les rgles gnrales obtenues et si possible dcouvrir des rgles encore plus
gnrales, sĠappliquant aux solides rguliers ou non et non seulement aux
hexadres examins. Ce que nous nous proposons de faire en continuant
dĠutiliser des modles sur cran dĠordinateur, en papier et les procds
dĠanalyse exposs ici. 2. Il faudra en
constituer un Atlas illustr des solides sans volume. Par exemple ceux drivs
des solides de Kpler, de Poinsot, dĠArchimde et de Johnson. 3. Puisque toute matire
tant gravide occupe un volume sinon il nĠy a pas de masse prsente, le prsent
travail dmontre la possibilit dĠune sorte de dmatrialisation des objets
matriels constituant les reprsentations des solides normaux puisquĠon
remplace leur forme pleine par une forme gomtrique creuse limite par des
plans et quĠon les amne logiquement ne possder aucun volume. Le solide sans
volume nĠenferme aucun volume. CĠest une manire de
remplacer la matire tridimensionnelle par une collection de surfaces, dont
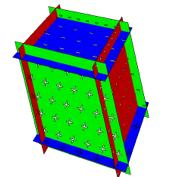
chacune est bidimensionnelle. 4. Cette sorte de
dmatrialisation est concrtise dans lĠexemple dĠun cube, matrialis par une
masse dĠeau cubique dans un rservoir cubique avec une paroi suprieure carre
B+ flottante et des parois latrales verticales. En ouvrant le robinet de vidange
situ dans sa paroi infrieure B-, il se vide, les parois B+ et B- entrent en
jonction et le cube solide est devenu sa manire un cube sans volume. Ë suivre. Remerciements. Nous remercions Pierre
Auger Ph.D. qui a calcul pour nous certains paramtres de nos pyramides. Rfrences. Rf. 1. Pierre Demers 2007, Systme du Qubcium, Solides sans
volume, Traduction interdite 1.
Surfaces nĠayant quĠun seul ct. Elles sont voques dans le
paragraphe: Ç Surface n'ayant qu'une face. Surfaces anti-Mbius.È. 2.
Les lignes suivantes dates de 2007 rclament une mise au point par leur
auteur. La voici en 2010, et dĠabord les lignes de lĠoriginal dont certaines
ont t mises en italiques. Ç Un suivi. Quelles consquences a) pour la thorie
gomtrique des solides, b) pour la thorie gnrale des symtries y compris
ses applications la thorie quantique de la matire?N.B.
XI2007. Une rdaction prcdente contenait une erreur : j'affirmais que tous
les solides normaux 1 11 possdaient une version sans volume. J'ai reconnu
que certains solides en sont dpourvus : Nos 3, 4,
5; et je rserve ma rponse pour les Nos 7 11. - La rdaction errone a t
retire, son adresse tait Systme du Qubcium. Cinq solides de Platon, 22
solides rguliers.
http://www.lisulf.quebec/CinqSPlaton22reguliers.html È Mise
au point. Je
ne vois plus de raisons pour refuser certains solides, rguliers ou non, la
capacit de devenir sans volume, cd, suivre le protocole convenu. Restera
apprcier dans chaque cas le degr de naturel, pertinence et intrt du
rsultat. Quant la thorie quantique de la matire et au projet imagin
par Kauffman, v. Rf. 2 qui suit : plutt que la topologie suggre par cet
auteur, jĠai suggr et commenc
dĠutiliser ce que jĠai appel gomtrie
quantique. Rf.
2.Louis H. Kauffman (1945-). http://www.math.uic.edu/~kauffman/A
tudi le ruban de Mbius et les nÏuds. A spcul sur leur utilisation et plus
gnralement lĠutilisation possible de la topologie pour ajouter la
description de la matire dans une continuit qui prolongerat celle amorce par
la mcanique ondulatoire de Louis de Broglie et la mcanique quantique de
Schrdinger. Voyez Gomtrie quantique selon Pierre Demers 2006, 2007 dans http://www.lisulf.quebec/quebecium.htm -30-  d
d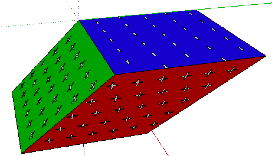 e
e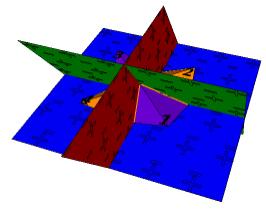 f
f
 b
b c
c
 b
b c
c
 e
e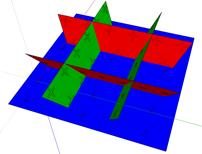 f
f
 b
b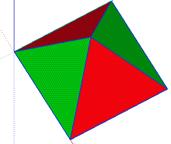 c
c
 d
d