Svisionbis19X2008 quebecium.html
Systme du
Qubcium.
Spin, vision et
principe de Pauli.
Pierre
Demers
Traduction interdite
Sommaire. Le tableau platonicien des lments chimiques reprsente les strates compltes par des solides rguliers tels le ttradre rgulier et le cube, chaque face de l'un de ces solides correspondant un lment. Or la reprsentation plane de ces solides ne peut pas montrer la totalit de leurs faces ni, par suite, des lments qu'ils sont censs figurer. A. Cette limitation suggre d'examiner la vision projective de ces solides et la perspective gomtrique. J'appelle vision d'un solide le nombre de faces que ce solide montre d'un coup d'oeil un observateur. La vision du cube est de 3 faces sur 6. La vision des 3 autres faces requiert une symtrie miroir. Quant au ttradre rgulier figurant les lments s ayant l = 0 : on peut le placer de manire que sa vision directe soit de 2 faces et sa vision miroir, des 2 autres faces. B. Vision directe et vision miroir correspondent spin - et spin + d'exclusion de Pauli ajoutant au modle atomique de Bohr. Le principe d'exclusion se trouve ds lors concrtis: il revient la ncessit, pour loger les lments de spin + une fois logs les lments de spin -, d'oprer une symtrie miroir. Qui donc a mis en scne la symtrie des miroirs faisant passer d'un monde un autre? Sinon Jean Cocteau. "Je vous livre le secret des secrets. Les miroirs sont les portes par lesquelles la Mort va et vient. Ne le dites personne". C. La symtrie miroir donne 2 visions des faces d'un solide, en analogie avec le principe faisant qu'il existe des lments chimiques de spin - et +. Augmentant le contenu physique du tableau platonicien, elle ajoute une dimension autrement cache.
Le tableau
platonicien des lments
chimiques.
Voyez ce tableau, qui apparat dans la rfrence 1. Le tableau platonicien des lments chimiques. Fig. 1.

Fig. 1. Le tableau platonicien des lments chimiques. La vision directe montre la moiti du nombre des faces et des lments : ce sont les lments s-; les autres faces sont visibles dans un miroir, les lments correspondants sont de spin +. 3platon120.gif
Les visions d'un
objet. L'observateur extrieur
l'objet.
La perception visuelle met en jeu un objet et un observteur qui lui est extrieur. Je la rapporte ici plutt l'objet. J'appelle vision d'un objet ce que cet objet offre la perception de l'observateur. Mon observateur est thorique, il regarde d'un seul oeil en ce qu'on appelle diversement Òprojection conventionnelle parallle ou cylindriqueÒ, ou Òperspective axonomtrique conventionnelle orthogonale."
Ainsi une sphre prsente invariablement une vision 2¹, parce qu'elle offre l'observateur, quel que soit son placement, la moiti de sa surface value 4¹ en angles solides. On peut placer un cube pour qu'il prsente une vision de 3 faces sur 6, un ttradre rgulier pour qu'il prsente une vision de 2 faces sur 4, Fig. 1. Ces visions du cube et du ttradre rgulier s'apparentent une vision 2¹ puisqu'elles montrent la moiti du nombre des faces. Des placements diffrents peuvent ne montrer qu'une vision rduite : par exemple une seule face cd 1/6 ou 1/4 de 4¹. Etc. Figs2, 3, 4. Les angles solides mentionns sont ceux rapports l'occupation angulaire vue du centre des figures.
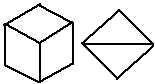
Fig. 2. Visions 2¹ : 3 faces du cube et 2 faces du ttradre rgulier.

Fig. 3. Une face du cube, vision 2¹/3; 2 faces du cube, vision 4¹/3 . Une face du ttradre rgulier, vision ¹; 3 faces du ttradre rgulier, vision 3¹. Le ttradre rgulier denier est une pyramide normale. Une pyramide normale peut montrer une seule face, elle peut montrer toutes ses faces sauf une.
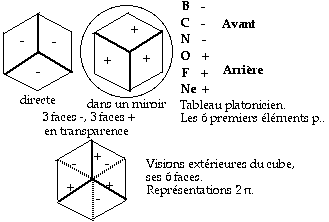
Fig. 4. Le cube, ses visions extrieures : directe, dans un miroir suppos plac l'arrire, en transparence. svfig4.gif
L'observateur
intrieur l'objet.
La description des solides platoniciens suppose des objets pleins, opaques et vus de leur extrieur. Mais supposons maintenant des objets, une sphre ou des solides, qui soient creux, et par suite rduits des surfaces, et l'observateur plac l'intrieur. Bornons-nous des surfaces convexes, sans parties rentrantes, cd que nous excluons les solides d'Euler et de Poinsot. Ë l'observateur, suppos centr ou non, ces objets prsentent une vision 4¹, laquelle est difficile suggrer dans une illustration plane, aussi bien que l'ensemble de la vote cleste comme les astronautes peuvent l'exprimenter, qu'une chambre dans un sous-marin ou dans une maison. Une sphre rflchissante place dans un jardin ou un objectif oeil de poisson couvrant 2¹ et davantage donnent une ide d'une telle vision. Puisque le champ visuel humain est approximativement une calotte d'angle solide 2¹, l'observateur muni d'un miroir plan obtient la vision complte 4¹ en 2 calottes.
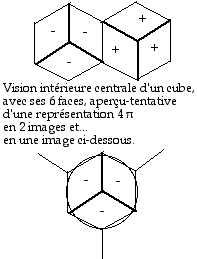
Fig. 5. Le cube, sa vision intrieure 4¹. svfig5.gif
L'observation externe d'un cube dtermine une vision comprenant 3 faces et limite 3 faces. Il ne peut en tre ainsi en observation interne. Je gnralise : les objets meublant notre paysage se prsentent pour tre connus de nous en observation externe. L'observation interne ne peut s'appliquer qu' un de ces objets la fois. Elle est en quelque sorte artificielle. La gomtrie habituelle se comprend par observation externe.
Formons une calotte sphrique en traant sur la sphre un cercle d'ouverture 90o, puis traons un 2e cercle de mme ouverture tangent au 1er. Puis un 3e de mme ouverture et tangent au 1er.et au 2e. Nous avons devant nous ce qu'il faut pour dlimiter 3 cnes avec leurs surfaces de rvoluton et leurs 3 surfaces appartenant chacune un plan. Or la rencontre de ces 3 plans forme un tridre trirectangle, que nous supposons plac au znith. En recommenant le processus autour du nadir, nous faisons apparatre 3 autres plans et 7 autres tridres trirectangles. Nous tenons un cube complet.
Ces dmarches proposent une logique de symtrie centrale pour le remplissage des faces du cube. Pour les lments p de spin - tels que B, C, N, il se fait naturellement sur 3 faces adjacentes formant un tridre; ensuite sur les 3 autres, de spin + : O, F, Ne.
Un processus analogue celui qui prcde est possible pour le ttradre rgulier. Le remplissage par les lments s de spin - tels que H, Li, se fait naturellement sur 2 faces fomant (ncessairement) un didre; ensuite sur les 2 autres, de spin + : He, Be.
La vision interne a donc l'intrt d'offrir, pour le remplissage des faces dans le tableau platonicien des lments, une dmarche ayant une symtrie centrale s'accordant avec celle des forces atomiques. Cette dmarche est humanise, puisqu'un observateur est ncessaire.
lments s et
p.
Ce qui prcde s'applique aux 16 lments s des strates 1, 2, 3, 4 et aux 36 lments p des strates 2, 3, 4.
lments d et
f.
Les 32 lments d des strates 3 et 4 en dehors de la colonne vertbrale, rpondent 4 rpartitions sur les faces de 4 octadres rguliers, au total 16 faces de spin - en vision directe et 16 de spin + en vision miroir.
Les 24 lments f de la strate 4 en dehors de la colonne vertbrale, rpondent des rpartitions sur les faces de 2 rhombododcadres rguliers, au total 12 faces de spin - en vision directe et 12 de spin + en vision miroir.
Les 12 lments d et f de la colonne vertbrale, soit 8 d et 4 f, sont traits comme s'ils taient des lments s avec l = 0. Ils sont rpartis sur les 12 faces de 3 ttradres rguliers.
Remerciements.
Je remercie Maurice Day pour d'utiles discussions sur la reprsentation plane des solides.
Rfrences.
1. Vers une gomtrie quantique bis. 7XI2007, Pierre Demers,
http://www.lisulf.quebec/Versgeometriequantiquebis.html,
2. Lonard de Vinci, qui essaya de rdiger un trait de la perspective, wiki, http://agora.qc.ca/mot.nsf/Dossiers/Leonard_de_Vinci, http://membres.lycos.fr/seddryck/ldvinci.html, http://www.devinci.fr/deploy/x-net/internet/institutionnel/accueil.1.html
3. Cours de gomtrie descriptive de l'cole d'architecture de Nancy. Wiki, GeoDescriptiveNancy, Thorie de la perspective et des projections
4. Claude Cossettehttp://www.comviz.com.ulaval.ca/module1/1.4_alphaiconique.php