Tableau3DOctaTT
Systme du
Qubcium.
3DOctadre
Tétraédrique Tétrades des Éléments. Tableau
3DOctaTT.
Pierre
Demers, EAPD.
Traduction
interdite.
6 au 20 X 2011. Modifi lr
12XI2011
Rsum. Ce tableau original est en 3D. Il est
form de 30 fois un octadre autres que de Platon, identique un ttradre
tronqu dĠArchimde, ayant 4 faces hexagones et 4 faces triangles, et en plus
dĠun certain nombre de fois un ttradre rgulier auxiliaire. LĠassemblage est
pavant et occupe exactement un ttradre de Platon. Chacun des octadres
reprsente une ttrade dĠlments. Le tableau a 4 strates dont 3 sont des
troncs ttradrique. On en donne des figurations 3D, 2D et manipulables dans
lĠespace. Ceci complte une prsentation prcdente. LĠanalyse du prsent
Tableau 3DOctaTT suggre des consquences que jĠespre examiner dans des publications
venir : peut-on en dduire une limitation au nombre des lments ?
peut-on le dduire de la thorie arithmtique des nombres premiers ?
Notre octadre.
On peut lĠobtenir
la manire dĠArchimde, en rduisant au tiers chaque arte dĠun ttradre de
Platon. Ou encore, on le construit partir de 4 hexagones rguliers et de 4
triangles quilatraux, tous de mme arte. Je prfre lĠappeler un octadre
plutt que ttradre tronqu dĠArchimde, afin de rappeler quĠil possde 8
faces. Patron de dcoupage et apeeus en projection plane. Figs 1, 2, 3.
1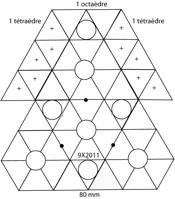 2
2 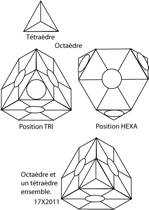 3
3
Figs 1, 2, 3. LĠoctadre et le ttradre
auxiliaire, patrons. Des cercles pour recevoir les critures. 1. Dcoupage sur carton
lger. Des pattes facilitent lĠassemblage. Les cases portant le signe + donnent
le ttradre auxiliaire. 2. Aperus en projection plane. Dans celle gauche,
la projection de lĠoctadre rduit la face hexagone au 1/3 de sa hauteur. De
lĠoctadre pos sur la table, on montre 2 positions principales, selon la face
visible par lĠobservateur :
une face hexagone sur la table = position
TRI ;
une face triangle sur la table = position HEXA.
Dans ce qui suit, les octadres sont dans lĠune ou
lĠautre de ces positions. 3. Voyez lĠimage manipulable dans lĠespace de Nouma.
Modèleocta9X2011.png, OctaTétraProjection.png, Rf. 2.
LĠoctadre a la
mme arte que le ttradre auxilaire mais des deux, le dernier a un volume
beaucoup plus petit. Les parois de lĠun et de lĠautre sont une collection de
triangles quilatraux gaux: 28 pour chaque octadre, dont 24 aux faces
hexagones et 4 aux faces triangles ; 4 pour chaque ttradre auxiliaire.
Dans leurs ralisations en 3D, on trouvera commode se contenter des faces hexagones
et dĠomettre les faces triangulaires.
Les positions principales de lĠoctadre. De
lĠoctadre pos sur la table Fig.
2 montre les 2 positions principales de notre choix: une face octadre sur la
table, une face triangle sur la table. Dans ce qui suit, les octadres sont
dans lĠune ou lĠautre de ces positions.
Le tableau 2D quart dĠellipse des lments chimiques.
Voici une version
mise jour du tableau 2D quart dĠellipse des lments. Rf. 1, Fig. 4.
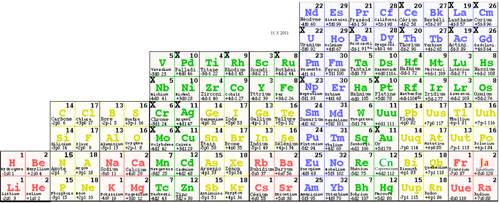
Fig. 4. Tableau quart dĠellipse des 120 lments,
ceux-ci tant groups en 30 ttrades. Ë lĠintrieur dĠune strate, une ttrade
groupe 4 lments ayant mme valeurs de l et de m, et une permutation de 2
caleurs de n et de s. DĠaprs Rf. 4 avec mise jour des cases 112 Cn
Copernicium et 120 Ja Janetium. 2DebTétradesbis.png
Voici ce mme
tableau rcrit afin de mettre en vidence les ttrades et leur composition.
Figs 5, 6, 7.
5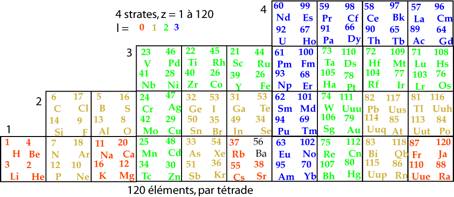
6
7
Figs 5, 6, 7.
Tableau 2D des 120 lments en ttrades. Idem, les ttrades tant dsignes par
le nom de leur 1er lment, de 1 87. Idem, les ttrades tant
dsignes par leur numro dĠordre, de 1 30. ParT́trade120.png,
Tétrades30,187.png, Tet́rades30,130.png,
Tableau original
3D en octadres ttradriques des lments en ttrades.
Voici, transform en
3D, le tableau Fig. 7, chaque ttrade tant reprsente par un octadre dcrit
Fig. 3. On imagine que chaque face hexagonale porte le nom de lĠun des lments
de la ttrade. Ë lĠintrieur dĠune strate, la collection des numros des
ttrades est impose, comme suit.
Strate 2. Ttrade 1............ = 1
ttrade (4 lments, z = 1 4)
Strate 2. Ttrades 2 5.....= 4 ttrades
(16 lments, z = 5 20)
Strate 3. Ttrades 6 14...= 9 ttrades
(36 lments, z = 21 56)
Strate 4. Ttrades 15 30.= 16 ttrades
(64 lments, z = 57 120)
En revanche, le placement de ces numros
lĠintrieur dĠune strate prte discussion. Je montre celui qui me semble le
plus naturel et dcoulant du placement 2D de Fig. 7.

Fig. 8. Tableau 3D des ttrades des lments, vue
en 2D des 4 strates et des 30 octadres. De chaque strate aprs la 1re, on a
figur sparment les octadres selon leur position principale, HEX ou TRI. Le
groupe HEX sĠembote dans le groupe TRI pour donner les troncs de ttradres
des strates 2, 3 et 4, aprs lĠaddition des ttradres auxiliaires. Les
ttradres. Strates123415X2011.png
Chaque strate complte, augmente au
besoin de ttradres complmentaires,
est un ttradre ou un tronc ttradrique. Voici ces 4 entits. Les
patrons Figs 9 13.
9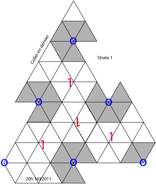 10
10 11
11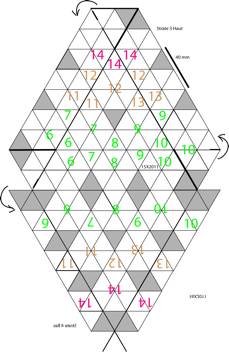 12
12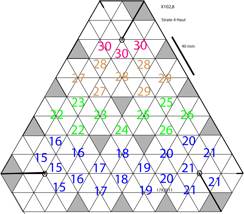 13
13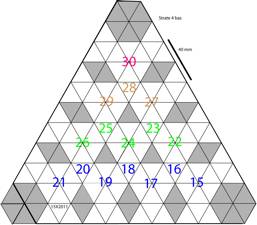
Figs 9 13. Les 4 strates : la 1re
en un ttradre, les suivantes en troncs ttradriques. Les patrons. Les
ttradres auxiliaires sont en gris. Strate116X2011.png,
Strate210h3016X2011.png, Strate316X2011.png, Strate4Haut17X2011.png, Strate4Bas17X2011.png
14 15
15 16
16
Figs 14, 15, 16. Les 4 strates : la
1re en un ttradre, les suivantes en troncs ttradriques. Vues. Les strates
isoles on montree le haut ; le bas. Idem runies composant un grand
ttradre. Les ttradres auxiliaires sont en gris.
Image13tétrastrates1234.png, ImageStratesBas.png,
Imageletétraocta4strates.png
Un caractre frappant de la distribution
des ttrades apparat Figs 14, 15, 16 et concerne les couleurs soit les
quanta azimutaux R pour l=0 et B pour l=3. Ces deux catgories forment des
barres, simple pour R et double pour B, orientes angle droit mutuellement.
Elles ne se touchent pas et dlimitent elles seules le volume du grand
ttradre Fig. 16.
Voici un dnombrement par strate.
Strate 1...1 octadre.......4 ttradres
auxiliaires.
Strate 2...4 octadres.....6 ttradres
auxiliaires.
Strate 3...9 octadres....11 ttradres
auxiliaires.
Strate 4...16 octadres..18 ttradres
auxiliaires.
Voici une image en ronde bosse de la
strate 4 avec les numros de quelques ttrades. Fig.17.

Fig. 17. Image en ronde bosse partielle de
la strate 4. Les ttrades TRI. ImageStrate4RBosse.png
Et voici une image manipulable 3D du grand
ttradre Figs 18, 19. 3DOctaTT
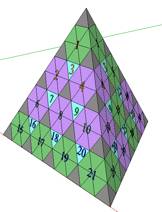
Figs 18, 19. Le grand ttradre. 18. Vue
2D de la vue 3D manipulable. 19. ImagedeSKP.png, ouvrir en dclenchant TETRAEDRE TRONQUEaugmente.skp, il faut ouvrir le logiciel Sketchup....
Discussion.
Ce qui prcde se ramne une distribution
de 30 nombres entiers allant de 1 30, munis de caractres quantiques dous de
signification physique. Elle confirme nouveau lĠintervention des symtries du
ttradre pour conprendre lĠorganisation de lĠatome.
Press par dĠautres besognes, jĠarrte ici
lĠanalyse du prsent Tableau 3DoctaTT, qui me semble poser des questions telles
que celles-ci. QuĠarriverait-il si on essayait dĠajouter une 5e
strate avec les 25 ttrades imaginaires quĠelle doit comporter?
Pourrait-on dduire de ce tableau une limitation au nombre des lments ?
Pourrait-on le dduire de la thorie des nombres premiers ? Ë suivre. Voir
Addition 12 XI 2011 Voir Rf. 6.
20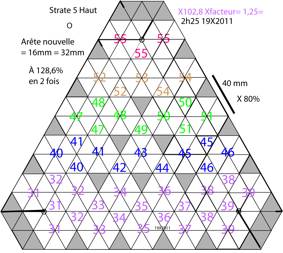 21
21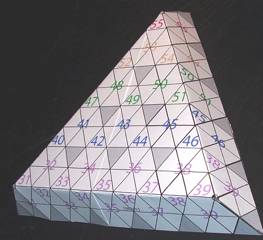
Figs 20, 21. Strate 5 haut, ttrades
imaginaires 31 55. Patron. Photo. Strate5Haut18X2011.png,
Strate5Haut20X2011.png
Remerciements.
Je remercie Patrick Demers pour son aide.
Addition le 12XI2011.
En examinant bien Fig. 19 sous tous les angles,
on constate que tous les numros de 1 30 sont lisibles sur au moins lĠune des
faces du ttradre compos de 4 strates, mme 24 sur le fond de la strate 4. CĠest
une face hexagonale numrote 24 dĠun octadre. Par contre, si on met en place
une strate 5, celle-ci obstrue la vue et empche de voir 24.
LĠagencement dĠune, deux, trois ou quatre
strates en un grand ttradre unique satisfait un critre de visibilit de tous
et chacun des octadres composants ; ce critre cesse dĠtre satisfait si
on envisage un grand ttradre de cinq strates.
On peut attribuer ce critre une interprtration
physique : une cinquime strate, avec 100 lments z = 121 220 est
impossible. Figs 22, 23.
22 23
23
Figs 22, 23. Agencement dĠune 5e
strate, Image11Strate5.pngImage11Strate5bis.png
Rfrences.
Rf. 1. Pierre Demers. Un tableau 2D des
lments quart dĠellipse
http://www.lisulf.quebec/QbTetrades.quart.gif
Rf.
2. Nouma. Ttradre tronqu manipulable dans lĠespace.
http://www.ac-noumea.nc/maths/polyhedr/classic/A_01.htm
Rf. 3. Systme du Qubcium. Un octadre
pavant et son usage dans un tableau 3D des lments chimiques. Traduction
interdite.
http://www.lisulf.quebec/Unoctaedrebis.htm
NB. Bien noter que
lĠoctadre lui seul nĠest pas pavant. Il lĠest associ au ttradre.
Rf. 4. Pierre Demers 2007, Qubcium International, Le Systme du
Qubcium et le Tableau elliptique des lments,
http://www.lisulf.quebec/conf.ClubSc.JdeB22II2007.html, Fig. 08.
Rf. 5. Pierre Demers. Systme du
Qubcium. Huit nombres premiers remarquables entre 1 et 30. Pierre Demers,
EAPD. Traduction interdite. 26IX2011.mj17X2011. Huit nombres premiers
remarquables.htm
Rf. 5. Pierre Demers.
Systme du Qubcium. Priodicits chez les nombres premiers.
Affinits avec le Systme du Qubcium. Pierre Demers, EAPD.
-30-