TableauTTR

En construction, m. à j. 1erX2104,

De la science en français.

Système du Québécium.

Un tableau des éléments

tout en rectangles,

basé sur les symétries géométriques

de l'écriture.

Pierre Demers.

12IX2014

M. à J. 9X2014

Traduction interdite.

1 ttr et TTR.

Pour désigner les tableaux présentés, je propose l'appellation abrégée ttr en minuscules pour les versions intermédiaires et TTR pour les résultats finaux.

Je propose une manière simplifiée d'accéder aux tableaux symétriques que j'ai publiés tels le tableau elliptique et le carré de carrés dernièrement: j'examine le graphisme du tableau traditionnel de 7 périodes occupant chacune une rangée. Je rappelle qu'il n'existe pas de solution rigoureuse de l'équation de Schrödinger sauf pour l'atome d'hydrogène, un proton et un électron, un problème de 2 corps.

Je le garde en rangées, dans l'ordre numérique des valeurs de z numéro atomique, en mettant en vedette par les couleurs RJVB selon les blocs ayant respectivement valeurs de l nombre azimutal. 0, 1, 2, 3, symbolisées par s, p, d, f..

2 Mendeleev.

Je pars donc du tableau bien connu de Mendeleev, dont voici deux exemplaires représentatifs contemporains. Figs 1, 2.

.1.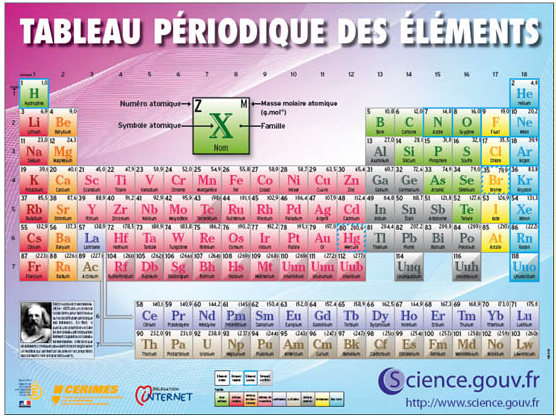

. 2

Figs 1, 2. Le tableau traditionnel, qui a rendu de grands services.

Tableau périodique des éléments chimiques, versions récentes: 1 Gouvernement français et 2 Jeantantout.

Dans Fig. 1, les 3 cases 113Uut, 115Uup et 117Uus ne sont pas tracées.

Excellent comme un répertoire ordonné et comparatif des éléments.

Trois longs espaces vides au début.

Les 2 dernières périodes se présentent avec alinéas et reprises.

On peut le découper en plusieurs rectangles, à la manière d'un ttr.

Périodique à peu près, symétrique guère.

On peut espérer mieux au point de vue symétrie.

Le placement des cases suggère qu'il recèlerait des symétries bien caractérisées et invite à faire mieux.

..

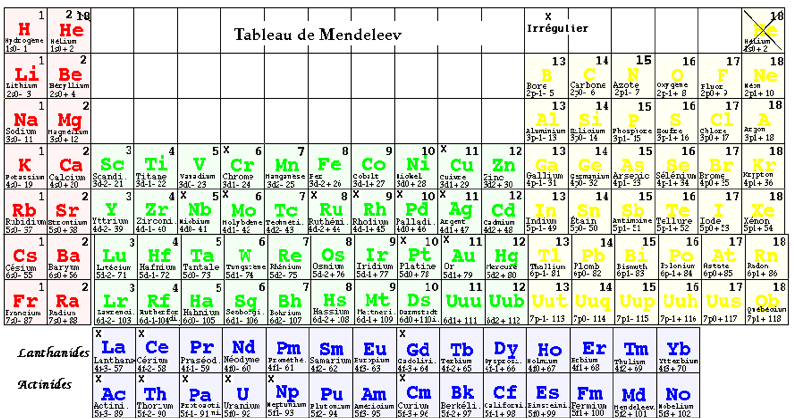Fig. 2bis. Le tableau de Mendeleev tel que je l'ai présenté en 2007.

....

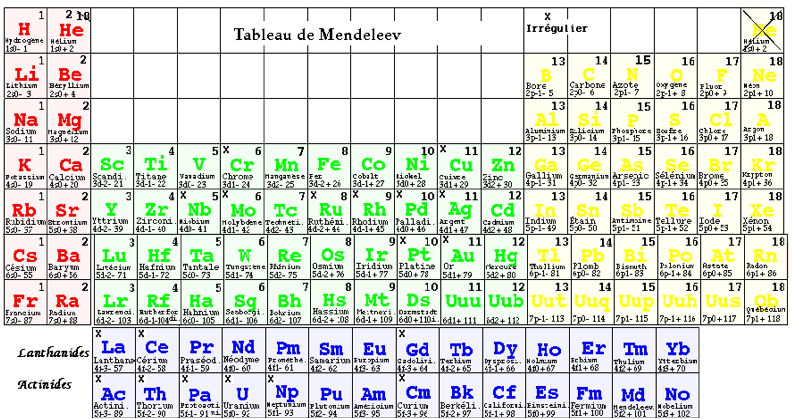Fig. 2ter. Mon tableau de Mendeleev tel que je le présenterais en 2014. Comme le précédent, augmenté de 119Uue et 120Ja.

Dans la version que j'adopte, Fig. 3. ce tableau traditionnel est un ttr de 7 rangées horizontales paralllèles de cases carrées représentant chacune un élément, une rangée par période se terminant sur un gaz rare. L'élément chimique est désigné par son numéro atomique z, allant de 1 à 118 et même 120, et par son symbole, incluant le québécium Qb ayant 118 protons et 118 électrons.

Dans chaque période: rouge le bloc s de 2 éléments, jaune le bloc p qui a 6 éléments, vert le bloc d de 10 éléments, bleu le bloc f de 14 éléments. Ces 4 couleurs sont fondamentales en science de la couleur. Les caractères spdf s'expriment, en théorie quantique, par des valeurs de l quantum azimutal 0, 1, 2, 3 de l'élément. Les 7 périodes se logent dans 32 colonnes, la 1re contient les alcalins , la dernière contient 6 gaz rares après He, celui-ci étant dans la colonne 2. Des cellules: imaginez des carrés tous de mêmes dimensions, non tracés par économie d'efforts, entourant l'écriture de chaque élément, contigus sur une même rangée de 32 colonnes.. Il a 224 cases dont 118 occupées.

1H 2He

3Li 4Be 5B 6C 7N 8O 9F 10Ne

11Na 12Mg 13Al 14Si 15P 16S 17Cl 18A

19K 20Ca 21Sc 22Ti 23V 24Cr 25Mn 26Fe 27Co 28Ni 29Cu 30Zn 31Ga 32Ge 33As 34Se 35Br 36Kr

37Rb 38Sr 39Y 40Zr 41Nb 42Mo 43Tc 44Ru 45Rh 46Pd 47Ag 48Cd 49In 50Sn 51Sb 52Te 53I 54Xe

55Cs 56Ba 57La 58Ce 59Pr 60Nd 61Pm 62Sm 63Eu 64Gd 65Tb 66Dy 67Ho 68Er 69Tm 70Yb 71Lu 72Hf 73Ta 74W 75Re 76Os 77Ir 78Pt 79Au 80Hg 81Tl 82Pb 83Bi 84Po 85At 86Rn

87Fr 88Ra 89Ac 90Th 91Pa 92U 93Np 94Pu 95Am 96Cm 97Bk 98Cf 99Es 100Fm 101Md 102No 103Lr 104Rf 105Ha 106Sg 107Bh 108Hs 109Mt 110Ds 111Rg 112Cn 113Uut 114Fl 115Uup 116Lv 117Uus 118Qb

Fig. 3. Un tableau ttr, 7 périodes en 7 rangées et 32 colonnes. Ce tableau est écrit en style justifié à gauche.

3 Écriture centrée.

Tout tableau plan, qu'il soit signé par Fortin ou par Mendeleev, est un graphisme. Soucieux de manifester des symétries, j'exploite la géométrie du graphisme sur papier ou écran: j'écris chaque rangée en style centré.

1H 2He

3Li 4Be 5B 6C 7N 8O 9F 10Ne

11Na 12Mg 13Al 14Si 15P 16S 17Cl 18A

19K 20Ca 21Sc 22Ti 23V 24Cr 25Mn 26Fe 27Co 28Ni 29Cu 30Zn 31Ga 32Ge 33As 34Se 35Br 36Kr

37Rb 38Sr 39Y 40Zr 41Nb 42Mo 43Tc 44Ru 45Rh 46Pd 47Ag 48Cd 49In 50Sn 51Sb 52Te 53I 54Xe

55Cs 56Ba 57La 58Ce 59Pr 60Nd 61Pm 62Sm 63Eu 64Gd 65Tb 66Dy 67Ho 68Er 69Tm 70Yb 71Lu 72Hf 73Ta 74W 75Re 76Os 77Ir 78Pt 79Au 80Hg 81Tl 82Pb 83Bi 84Po 85At 86Rn

87Fr 88Ra 89Ac 90Th 91Pa 92U 93Np 94Pu 95Am 96Cm 97Bk 98Cf 99Es 100Fm 101Md 102No 103Lr 104Rf 105Ha 106Sg 107Bh 108Hs 109Mt 110Ds 111Rg 112Cn 113Uut 114Fl 115Uup 116Lv 117Uus 118Qb

Fig. 4. Comme Fig. 3. Un autre tableau de 7 périodes en 7 rangées.

NB. Attention, note de lecture: seon le réglage en largeur sur l'ordinateur, les rangées les plus longues peuvent s'afficher avec repli et alinéation dans Fig 3 et suivantes.

Voilàun progrès au point de vue symétrie. Fig. 4 a évidemment un axe central vertical de symétrie gauche - droite quant aux nombres des cases occupées sur chaque rangée.

4 Nombre magique 2.

Figs 3 et 4. Ces figures répondent au nombre magique 2: chaque rangée, divisée en 2 parties égales contient un nombre pair de cellules occupées, aussi bien que l'ensemble du tableau.

5 Le cas de l'hélium. La considération chimique.

Dans l'écriture choisie, la couleur R appartient à l'hydrogène, à l'hélium aussi bien qu'aux alcalins et aux alcalino-terreux y compris le béryllium.

La considération chimique: je place au second rang la considération chimique que l'hélium n'est pas un alcalino-terreux.

Dans la considération électronique, rouge R, quantum azimutal l = 0 et symbole s sont synonymes.

6 Nombre magique 2. Symétrie droite - gauche numérique. La considération couleur.

Dans chaque rangée, tous les tableaux Figs 3 à 5 présentent un nombre pair de cases occupées, répondant donc au nombre magique 2, utilisant la notion de nombre magique, qui a fait fortune en théorie du noyau.

Au point de vue numérique, il y a donc symétrie droite - gauche, mais, dans Fig. 5, pas au point de vue couleurs, sauf dans la 1re période.

7 Bidimensionnel. Deux dimensions pour une période. Une rangée pour chaque bloc.

Mais pourquoi limiter à une dimension l'écriture des périodes? Le support papier ou écran en accorde 2. J'accorde à chaque période la bidimensionnalité et j'étends sa représentation selon la verticale en plaçant chaque bloc dans une rangée distincte. Un bloc se distingue, à l'intérieur d'une période, par une couleur et un quantum azimutal l constants; il y a 19 blocs. Je préserve l'association des blocs selon les 7 périodes traditionnelles en les séparant par des lignes intercalaires portant un point noir.

1H 2He

•

3Li 4Be

5B 6C 7N 8O 9F 10Ne

•

11Na 12Mg

13Al 14Si 15P 16S 17Cl 18A

•

19K 20Ca

21Sc 22Ti 23V 24Cr 25Mn 26Fe 27Co 28Ni 29Cu 30Zn

31Ga 32Ge 33As 34Se 35Br 36Kr

•

37Rb 38Sr

39Y 40Zr 41Nb 42Mo 43Tc 44Ru 45Rh 46Pd 47Ag 48Cd

49In 50Sn 51Sb 52Te 53I 54Xe

•

55Cs 56Ba

57La 58Ce 59Pr 60Nd 61Pm 62Sm 63Eu 64Gd 65Tb 66Dy 67Ho 68Er 69Tm 70Yb

71Lu 72Hf 73Ta 74W 75Re 76Os 77Ir 78Pt 79Au 80Hg

81Tl 82Pb 83Bi 84Po 85At 86Rn

•

87Fr 88Ra

89Ac 90Th 91Pa 92U 93Np 94Pu 95Am 96Cm 97Bk 98Cf 99Es 100Fm 101Md 102No

103Lr 104Rf 105Ha 106Sg 107Bh 108Hs 109Mt 110Ds 111Rg 112Cn

113Uut 114Fl 115Uup 116Lv 117Uus 118Qb

Fig. 5. Tableau par périodes traditionnelles une rangée par bloc. Il y a 19 rangées et 32 colonnes, 32*19 = 608 cases dont 118 occupées.

Voilà un nouveau progrès: il y a dans Fig. 5 une évidente symétrie des couleurs dans chaque rangée.

8 Pairage et disparité.

Fig. 6, j'écris la longueur des périodes successives en nombres de termes dans les figures 3, 4 et 5. D'abord le numéro de la période, de 1 à 7

1 2

2 8

3 8

4 14

5 14

6 32

7 32

Fig. 6.

Par le nombre des cases occupées, 1re période se distingue des 6 suivantes: elle apparaît isolée, alors que les 6 suivantes apparaissent par paires. Il y a disparité de la 1re période, les périodes se succèdent comme suit.

1 isolée

2 pairée

3 pairée

4 pairée

5 pairée

6 pairée

7 pairée

Fig. 7. Disparité de la période 1, isolée. Il y a 6 périodes pairées et 1 isolée.

C'est là un défaut de symétrie. Il manque un sorte de symétrie selon la verticale entre les pairages des périodes.

Mais je reprends Fig. 5 en supprimant les lignes intercalaires qui portent un point et séparent les périodes traditionnelles. Le résultat est un tableau des blocs. La lecture des numéros atomiques z reste consécutive, de 1 à 118.

1H 2He

3Li 4Be

5B 6C 7N 8O 9F 10Ne

11Na 12Mg

13Al 14Si 15P 16S 17Cl 18A

19K 20Sr

21Sc 22Ti 23V 24Cr 25Mn Mn 26Fe 27Co 29Cu 30Zn

31Ga 32Ge 33As 34Se 35Br 36Kr

37Rb 38Sr

39Y 40Zr 41Nb 42Mo 43Tc 44Ru 45Rh 46Pd 47Ag 48Cd

49In 50Sn 51Sb 52Te 53I 54Xe

55Cs 56Ba

57La 58Ce 59Pr 60Nd 61Pm 62Sm 63Eu 64Gd 65Tb 66Dy 67Ho 68Er 69Tm 70Yb

71Lu 72Hf 73Ta 74W 75Re 76Os 77Re 78Ir 79Pt 80Hg

81Tl 82Pb 83Bi 84Po 85At 86Rn

87Fr 88Ra

89Ac 90Th 91Pa 92U 93Np 94Pu 95Am 96Cm 97Bk 98Cf 99Es 100Fm 101Md 102No

103Lr 104Rf 105Ha 106Sg 107Bh 108Hs 109Mt 110Ds 111Rg 112Cn

113Uut 114Fl 115Uup 116Lv 117Uus₁ 118Qb

Fig. 8. Tableau par blocs. Il y a 19 blocs.

C'est un tableau en blocs, et il a 19 rangées contenant chacun un bloc. C'est encore un ttr. Par le nombre de cases occupées dans chaque rangée, Fig. 8 présente elle aussi une symétrie droite - gauche, donc de nombre magique 2. Il manque une sorte de symétrie selon la verticale dans l'organisation des rangées successives, la 1re rangée fait bande à part, il est habituel de la présenter isolée, alors que chaque autre rangée R vient associée avec une 2e qui la suit comme dans Fig. 5.

9 Nouvelle définition des périodes.

Dans l'espoir d'améliorer la symétrie selon a verticale, je modifie Fig. 8 en ajoutant des lignes intercalaires ou, ce qui revient au même, je reprends Fig 5 en déplaçant d'une ligne vers le bas, les lignes intercalaires portant un point.

1H 2He

3Li 4Be

•

5B 6C 7N 8O 9F 10Ne

11Na 12Mg

•

13Al 14Si 15P 16S 17Cl 18A

19K 20Ca

•

21Sc 22Ti 23V 24Cr 25Mn 26Fe 27Co 28Ni 29Cu 30Zn

31Ga 32Ge 33As 34Se 35Br 36Kr

37Rb 38Sr

•

39Y 40Zr 41Nb 42Mo 43Tc 44Ru 45Rh 46Pd 47Ag 48Cd

49In 50Sn 51Sb 52Te 53I 54Xe

55Cs 56Ba

•

57La 58Ce 59Pr 60Nd 61Pm 62Sm 63Eu 64Gd 65Tb 66Dy 67Ho 68Er 69Tm 70Yb

71Lu 72Hf 73Ta 74W 75Re 76Os 77Ir 78Pt 79Au 80Hg

81Tl 82Pb 83Bi 84Po 85At 86Rn

87Fr 88Ra

•

89Ac 90Th 91Pa 92U 93Np 94Pu 95Am 96Cm 97Bk 98Cf 99Es 100Fm 101Md 102No

103Lr 104Rf 105Ha 106Sg 107Bh 108Hs 109Mt 110Ds 111Rg 112Cn

113Uut 114Fl 115Uup 116Lv 117Uus 118Qb

Fig. 9. Tableau par périodes nouvelles, étape vers un-

L'ordre d'écriture et l'ordre de lecture des nombres atomiques restent inchangés.

Telle qu'elle se présente, Fig. 9 satisfait certains de mes besoins de symétrie. La lecture des numéros atomiques est consécutive de 1 à 118. Au début du tableau, apparaît une 2e période, la 1re période se trouve pairée avec une nouvelle période de même longueur. Il y a 8 périodes.

Mais la 8e et dernière souffre d'une disparité: toutes se terminent sur 2 rouges, sauf la dernière. La disparité unique des figures précédentes au début est remplacée par 2 disparités à la fin. Il y a un total de 8 périodes, je compte 6 périodes pairées et 2, les 7e et 8e, isolées. J'écris Fig. 10 pour le signaler. Comparer avec Fig. 7.

1 pairée

2 pairée

3 pairée

4 pairée

5 pairée

6 pairée

7 isolée

8 isolée

Fig. 10. Disparité dans Fig. 8 des périodes 7 et 8, isolées. Il y a 6 périodes pairées et 2 isolées.

Ce manque de symétrie est facilement réparé: j'ajoute, à la 8e période, une 4e rangée de 2 R : 119Uue et 120Ja pour Janetium. Voici.

1H 2He

3Li 4Be

•

5B 6C 7N 8O 9F 10Ne

11Na 12Mg

•

13Al 14Si 15P 16S 17Cl 18A

19K 20Ca

•

21Sc 22Ti 23V 24Cr 25Mn 26Fe 27Co 28Ni 29Cu 30Zn

31Ga 32Ge 33As 34Se 35Br 36Kr

37Rb 38Sr

•

39Y 40Zr 41Nb 42Mo 43Tc 44Ru 45Rh 46Pd 47Ag 48Cd

49In 50Sn 51Sb 52Te 53I 54Xe

55Cs 56Ba

•

57La 58Ce 59Pr 60Nd 61Pm 62Sm 63Eu 64Gd 65Tb 66Dy 67Ho 68Er 69Tm 70Yb

71Lu 72Hf 73Ta 74W 75Re 76Os 77Ir 78Pt 79Au 80Hg

81Tl 82Pb 83Bi 84Po 85At 86Rn

87Fr 88Ra

•

89Ac 90Th 91Pa 92U 93Np 94Pu 95Am 96Cm 97Bk 98Cf 99Es 100Fm 101Md 102No

103Lr 104Rf 105Ha 106Sg 107Bh 108Hs 109Mt 110Ds 111Rg 112Cn

113Uut 114Fl 115Uup 116Lv 117Uus 118Qb

119Uue 120Ja

Fig. 11. Tableau en 8 périodes nouvelles, TTR.

Voilà. J'obtiens un tableau TTR de 8 périodes toutes pairées, sans disparité. Il y a 120 éléments. Chaque période se termine sur 2 éléments s, couleur rouge R

1 pairée

2 pairée

3 pairée

4 pairée

5 pairée

6 pairée

7 pairée

8 pairée

Fig. 12. Aucune disparité dans Fig. 11. Il y a 8 périodes pairées et aucune isolée.

Et voilà; 8 puissance de 2 ce qui est satisfaisant.

10 Bidimensionnel A. Deux dimensions accessibles pour un bloc. Des crochets et des demi-crochets de cases.

J'applique cette convention: de répartir les cases d'un bloc ayant plus que 2 termes sur 2, 3 ou 4 rangées; je choisis des répartitions contigües dessinant des crochets de typographie conventionnels ouvrants tournés de 90o vers le bas dans le sens d'une aiguilles d'une montre, comme suit. Fig. 13.

1H 2He

•

3Li 4Be

•

6C 7N 8O 9F

5B 11Na 12Mg 10Ne

•

14Si 15P 16S 17Cl

13Al 19K 20Ca 18A

•

23V 24Cr 25Mn 26Fe 27Co 28Ni

22Ti 32Ge 33As 34Se 35Br 29Cu

21Sc 31Ga 37Rb 38Sr 36Kr 30Zn

•

41Nb 42Mo 43Tc 44Ru 45Rh 46Pd

40Zr 50Sn 51Sb 52Te 53I 47Ag

39Y 49In 55Cs 56Ba 54Xe 48Cd

•

60Nd 61Pm 62Sm 63Eu 64Gd 65Tb 66Dy 67Ho

59Pr 72Hf 74W 75Re 76Os 77Ir 78Pt 68Er

58Ce 73Ta 82Pb 83Bi 84Po 85At 79Au 69Tm

57La 71Lu 81Tl 87Fr 88Ra 86Rn 80Hg 70Yb

•

92U 93Np 94Pu 95Am 96Cm 97Bk 98Cf 99Es

91Pa 105Ha 106Sg 107Bh 108Hs 109Mt 110Ds 100Fm

90Th 104Rf 114Fl 115Uup 116Lv 117Uus 111Rg 101Md

89Ac 103Lr 113Uut 119Uue 120Ja 118Qb 112Cn 102No

Fig. 13. Tableau TTR par périodes nouvelles, graphisme en crochets ouvrants tournés de 90o vers le bas. Chaque crochet est formé de 2 demi-crochets.

Tableau par périodes nouvelles, en 8 rectangles occupés, TTR.

Le résultat est une suite de 8 périodes où je lis les numéros atomiques dans l'ordre. Les nombres d'éléments dans les périodes successives sont comme suit. Fig. 14.

1 2

2 2

3 8

4 8

5 18

6 18

7 32

8 32

Fig. 14. Nombres d'éléments dans les périodes successives Fig. 13. Il y a 8 périodes chacune pairée et aucune isolée.

Pour des raisons que la suite éclaircira, je pourrais réécrire Fig. 13 en inversant l'ordre d'écriture dans les demi-crochets. Réf. 3. Fig. 15

1H 4Be

•

3Li 2He

•

6C 5B 8O 9F

7N 11Na 12Mg 10Ne

•

etc

Fig. 15. Tableau TTR par périodes nouvelles, graphisme en crochets ouvrants tournés de 90o vers le bas. Chaque crochet est formé de 2 demi-crochets.

Tableau par périodes nouvelles, en 8 rectangles occupés, TTR.

Un demi-crochet est une équerre symétrique.

11 Des strates. Quatre strates chacune renfermant deux périodes d'égales longueurs.

Des strates. J'associe les périodes consécutives de chaque paire de celles-ci pour en former ce que j'appelle une strate. Il y a 4 strates.

Lecture. Dans les strates 2, 3 et 4, je lis la suite des numéros atomiques en commençant en bas à gauche de sa 1re période.

À une strate, j'attribue une couleur RJVB, celle de l'élément de 1re lecture. Fig. 15, où j'ai ajouté du vert vif comme couleur de surlignage.

1re strate.

1H 2He

•

3Li 4Be

•

2e strate.

6C 7N 8O 9F

5B 11Na 12Mg 10Ne

•

14Si 15P 16S 17Cl

13Al 19K 20Ca 18A

•

3e strate.

23V 24Cr 25Mn 26Fe 27Co 28Ni

22Ti 32Ge 33As 34Se 35Br 29Cu

21Sc 31Ga 37Rb 38Sr 36Kr 30Zn

•

41Nb 42Mo 43Tc 44Ru 45Rh 46Pd

40Zr 50Sn 51Sb 52Te 53I 47Ag

39Y 49In 55Cs 56Ba 54Xe 48Cd

•

4e strate.

60Nd 61Pm 62Sm 63Eu 64Gd 65Tb 66Dy 67Ho

59Pr 72Hf 74W 75Re 76Os 77Ir 78Pt 68Er

58Ce 73Ta 82Pb 83Bi 84Po 85At 79Au 69Tm

57La 71Lu 81Tl 87Fr 88Ra 86Rn 80Hg 70Yb

•

92U 93Np 94Pu 95Am 96Cm 97Bk 98Cf 99Es

91Pa 105Ha 106Sg 107Bh 108Hs 109Mt 110Ds 100Fm

90Th 104Rf 114Fl 115Uup 116Lv 117Uus 111Rg 101Md

89Ac 103Lr 113Uut 119Uue 120Ja 118Qb 112Cn 102No

Fig. 15. Tableau TTR en 4 strates des 120 éléments. À gauche spin -, à droite spin +. Surlignage en vert vif.

Strates 1 et 2. Constitutifs des vivants.

Strate 3 et Strate début. Utilitaires pour les humains.

Strate 4 fin. Instables.

Un aspect de la matière universelle: un arbre de Noël, vert en tout temps au pays du Québécium.

En faire un vitrail? V. à la fin.

Modifier l'ordre des entrées dans les crochets? Voir Réf. 3

Et voilà un TTR en 4 strates des 120 éléments.

À suivre. Il est midi HAE mercredi 1erX2014.

Le tableau Fig. 15 a 20 rangées. Le voici récrit sans superflus. Fig. 16.

- s +

1H 2He

3Li 4Be

6C 7N 8O 9F

5B 11Na 12Mg 10Ne

14Si 15P 16S 17Cl

13Al 19K 20Ca 18A

23V 24Cr 25Mn 26Fe 27Co 28Ni

22Ti 32Ge 33As 34Se 35Br 29Cu

21Sc 31Ga 37Rb 38Sr 36Kr 30Zn

41Nb 42Mo 43Tc 44Ru 45Rh 46Pd

40Zr 50Sn 51Sb 52Te 53I 47Ag

39Y 49In 55Cs 56Ba 54Xe 48Cd

60Nd 61Pm 62Sm 63Eu 64Gd 65Tb 66Dy 67Ho

59Pr 72Hf 74W 75Re 76Os 77Ir 78Pt 68Er

58Ce 73Ta 82Pb 83Bi 84Po 85At 79Au 69Tm

57La 71Lu 81Tl 87Fr 88Ra 86Rn 80Hg 70Yb

92U 93Np 94Pu 95Am 96Cm 97Bk 98Cf 99Es

91Pa 105Ha 106Sg 107Bh 108Hs 109Mt 110Ds 100Fm

90Th 104Rf 114Fl 115Uup 116Lv 117Uus 111Rg 101Md

89Ac 103Lr 113Uut 119Uue 120Ja 118Qb 112Cn 102No

Fig. 16. Comme Fig. 15, sans superflus. En signalant spins - à gauche et + à droite. Chaque période est devenue un rectangle dont la largeur est le double de sa hauteur. Chaque strate est un carré. Pour chaque spin, ii apparaît des crochets emboîtés. de cases, successivement autour d'une case R: 3 J. 5 V, 7 B. Fig. 16bis

12 Équerres de cases.

Deux demi - équerres de cases composent un crochet. Chaque crochet contient 2 équerres opposées horizontalement. Fig. 16bis.

BBBB

BVVV

BVJ J

BVJR

Fig.16bis. Schéma de l'emboîtage. Deux équerres opposées horizontalement forment un crochet. Deux crochets opposés forment un cadre..

11 Symétriser haut - bas dans chaque strate.

Dans chaque strate, la symétrie gauche - droite se manifeste; il est opportun que j'établisse une symétrie haut - bas. Rien à changer à la strate 1. Mais il faut que j'inverse l'ordre des rangées dans chaque 2e période des strates 2, 3 et 4. Voilà aux Figs 17.

- s +

1H 2He

3Li 4Be

6C 7N 8O 9F

5B 11Na 12Mg 10Ne

13Al 19K 20Ca 18A

14Si 15P 16S 17Cl

23V 24Cr 25Mn 26Fe 27Co 28Ni

22Ti 32Ge 33As 34Se 35Br 29Cu

21Sc 31Ga 37Rb 38Sr 36Kr 30Zn

39Y 49In 55Cs 56Ba 54Xe 48Cd

40Zr 50Sn 51Sb 52Te 53I 47Ag

41Nb 42Mo 43Tc 44Ru 45Rh 46Pd

60Nd 61Pm 62Sm 63Eu 64Gd 65Tb 66Dy 67Ho

59Pr 72Hf 74W 75Re 76Os 77Ir 78Pt 68Er

58Ce 73Ta 82Pb 83Bi 84Po 85At 79Au 69Tm

57La 71Lu 81Tl 87Fr 88Ra 86Rn 80Hg 70Yb

89Ac 103Lr 113Uut 119Uue 120Ja 118Qb 112Cn 102No

90Th 104Rf 114Fl 115Uup116Lv 117Uus 111Rg 101Md

91Pa 105Ha 106Sg 107Bh 108Hs 109Mt 110Ds 100Fm

92U 93Np 94Pu 95Am 96Cm 97Bk 98Cf 99Es

Fig. 17. Dans les strates 2, 3, 4, dans la 2e période, l'ordre des rangées de Fig. 16 a été inversé. Dans les strates 2, 3 et 4, les crochets B, V, J se rejoignent pour se refermer complètement sur le rectangle massif R. Le résultat est un autre TTR.

Dans chaque strate, un pâté de 4 cases R.

Dans les strates 2, 3, 4, ce pâté est encadré concentriquement de cadres de cases , les cadres disponibles étant 12J, 20V, 28B.

13 Chaque strate en 4 quadrants

Ces quadrants sont désignés par les points cardinaux intermédiaires. NO, SO, SE et NO. Fig. 18

NO | NE

s- ------|----- s+

SO | SE

Fig. 18. Chaque strate est divisible en 4 quadrants NO, SO, SO, SE, selon les 4 points cardinaux intermédiaires.

Les quadrants O sont de spin -, les qudrants E, de spin =. Chaque quadrant comprend au moins une cellule s. Il comprend 1, 4, 9 ou 16 cases, ces nombres sont les carrés du numéro de la strate. Les strates apparaissent comme des rectangles, mais elles sont des carrés aplatis, puisque j'ai choisi jusqu'ici de ne pas dessiner les cases carrées. Par exemple, la strate 4 a 8 cases de large et 8 cases de haut.

14 Des équerres emboîtées.

Ces équerres sont formées de 3, 5 ou 7 cases et s'emboîtent autour de 2 côtés de la cellule s du quadrant.

Nombre de cases dans les quadrants.

Je répète: chaque quadrant comprend au moins une cellule, qui est s rouge. Il comprend 1, 4, 9 ou 16 cases, ces nombres sont les carrés du numéro de la strate.

La somme de ces nombres est 30, confirmant que le nombre total des cases du tableau et le nombre des éléments est 120 = 4*30.

Correctement figurées, chaque demi-strate est un rectangle, chaque strate est un carré.

15 Nombres magiques 2, 4, 8, 30 et 120.

Importants: 2 et 8, puisqu'il y a 8 strates; 4, 30 et leur produit 120 sont des nombres magiques du tableau périodique des éléments, càd, des atomes. Aussi bien que les célèbres nombres magiques du noyau 2, 8, 20, 28, 50, 82 et 126. Je mentionne la règle de l'octet en chimie et l'évocation des symétries du cube par G. N. Lewis. Un cube a 8 sommets et 6 faces. Il circonscrit le tétraèdre qui a 6 arêtes, 4 sommets et 4 faces.

16 Écriture des caractères.

s

Je reconnais un élément par z numéro atomique et par les 4 caractères quantiques de l'électron de valence s, n, l, m. Jusqu'ici j'ai pu me contenter d'en figurer l, nombre azimutal qui vaut 0, 1, 2 ou 3 synonymes des notations s, p, d et f, par la couleur R, J, V ou B. Afin de poursuivre, il m'est nécessaire d'inscrire ces 4 caractères dans chaque case, y compris les notations s, p, d ou f en redondance. Fig. 19.

			1H-1s0	2He+1s0
			3Li-2s0	4Be+2s0
		6C-2p0	7N-2p1	8O+2p-1	9F+2p0
		5B-2p-1	11Na	12Mg+3s0	10Ne+2p1
		13Al-3p1	19K-4s0	20Ca+4s0	18A+3p1
		14Si-3p0	15P-3p1	16S+3p-1	17Cl+3p0
	23V-3d0	24Cr-3d1	25Mn=3d2	26Fe+3d-2	27Co+3d-1	28Ni+3d0
	22Ti-3d-2	32Ge-4p0	33As-4p1	34Se+4p-1	35Br+4p0	29Cu+3d1
	21Sc-3d-2	31Ga-4p-1	37Rb-5s0	38Sr+5s0	36Kr+4p1	30Zn+3d2
	39Y-4d-2	49In-5p-1	55Cs-6s0	56Ba+6s0	54Xe+5p1	48Cd+4d2
	40Zr-4d-1	50Sn-5p0	51Sb-5p1	52Te+5p-1	53I+5p0	47Ag+4d1
	41Nb-4d0	42Mo-4d1	43Tc-4d2	44Ru+4d-2	45Rh+4d-1	46Pd+4d0
60Nd-4f0	61Pm-4f1	62Sm-4f2	63Eu-4f3	64Gd+4f-3	65Tb+4f-2	66Dy+4f-1	67Ho+4f0
59Pr-4f-1	73Ta-5d0	74W-5d1	75Re-5d2	76Os+5d-2	77Ir+5d-1	78Pt+5d0	68Er+4f1
58Ce-4f-2	72Hf-5d-1	82Pb-6p0	83Bi-6p1	84Po+6p-1	85At+6p0	79Au+5d1	69Tm+4f2
57La-4f-3	71Lu-5d-2	81Tl-6p-1	87Fr-7s0	88Ra+7s0	86Rn+6p1	80Hg+5d2	70Yb+4f3
89Ac-5f3	103Lr-6d-2	113Uut-7p1	119Uue-8s0	120Ja+8s0	118Qb+7p1	112Cn+6d2	102No+5f3
90Th-5f2	104Rf-6d1	114Fl-7p0	115Uup-7p1	116Lv+7p-1	117Uus+7p0	111Rg+6d1	101Md+5f2
91Pa-5f1	105Ha-6d0	106Sg-6d1	107Bh-6d2	108Hs+6d-2	109Mt+6d-1	110Ds+6d0	100Fm+5f1
92U-5f0	93Np-5f1	94Pu-5f2	95Am-5f3	96Cm+5f-3	97Bk+5f-2	98Cf+5f-1	99Es+5f0

Fig. 19. La formule électronique complète d'un atome est la somme de ce qui lui est attribué dans sa case propre et dans toutes les cases qui précèdent la sienne. Ces valeurs sont nominales et ne tiennent pas compte des irrégularités, voyez Réf. 4.

Ainsi, la formule complète du janétium Ja 120 commence par -1s0 +1s0 ... et se termine avec ... +7p1 -8s0 +8s0.

Ce sont là les caractères nominaux, 19 éléments ne se conforment pas à cette liste et sont appelés irréguliers. Ils sont marqués d'une astérisque dans Fig. 2bis et ci-dessous.

17 Réorienter le tableau.

Selon les 4 orientations principales, avec les 4 aplombs de l'écriture. Un 1er essai, grâce à Maurice Day. Figs 19, 20.

Fig. 20. Essai 1 des aplombs strates 1 et 2.

Fig. 21. Essai bis des aplombs des strates 1 et 2

Fig. 22. Essai ter des aplombs des strates 1 et 2

Fig. 23. Essai quater des aplombs des strates 1 et 2.

En assemblant des collections de tels graphismes, on pourrait présenter des tableaux dont toutes seraient lisibles d'aplomb, ayant la 1re strate en haut, en bas, à gauche ou à droite.

18 Symétries par rapport à un point.

Chaque strate présente une symétrie de rotation de 90o quant aux couleurs. Cela me suggère d'expérimenter ces symétries d'une strate à la fois.

À suivre. 11h06 jeudi 2X2014

Une symétrie par rapport à un point signifie une symétrie par rapport à un axe linéaire passant par ce point, augmentée d'une symétrie par rapport à un autre axe linéaire à angle droit par rapport au précédent, passant par le même point. Ces axes sont symbolisés pourla strate 1 dans le tableau Fig. 22, soit 1o selon les axes NS, EO, soit 2o en X selon les axes intermédiaires à 45o qui sont eux=mêmes une ligne neutre. Il faut garder les termes dans leur colonne. Inutile de changer l'ordre dans la colonne 1. Le seul changement possible est d'échanger les termes dans la colonne 2, ce qui revient à 1o. La symétrie par

-|+

1H-1s0

2He+1s0

-X-

3Li-2s0

4Be+2s0

|

devient

1H-1s0

4Be+2s0

3Li-2s0

2He+2s0

Fig. 24. Opération de symétrie selon X sur la strate 1. La lecture se fait 1234, en zigzag.

Voici un essai sur la strate 4.

-|+

60Nd-4f0	61Pm-4f1	62Sm-4f3	63Eu-4f3	64Gd+4f-3	65Tb+4f-2	66Dy+4f-1	67Ho+4f0
59Pr-4f-1	73Ta-5d0	74W-5d1	75Re-5d2	76Os+5d-2	77Ir+5d-1	78Pt+5d0	68Er+4f1
58Ce-4f-2	72Hf-5d-1	82Pb-6p0	83Bi-6p1	84Po+6p-1	85At+6p0	79Au+5d1	69Tm+4f2
57La-4f-3	71Lu-5d-2	81Tl-6p-1	87Fr-7s0	88Ra+7s0	86Rn+6p1	80Hg+5d2	70Yb+4f3

-X-

89Ac-5f3	103Lr-6d-2	113Uut-7p1	119Uue-8s0	120Ja+8s0	118Qb+7p1	112Cn+6d2	102No+5f3
90Th-5f2	104Rf-6d1	114Fl-7p0	115Uup-7p1	116Lv+7p-1	117Uus+7p0	111Rg+6d1	101Md+5f2
91Pa-5f1	105Ha-6d0	106Sg-6d1	107Bh-6d2	108Hs+6d-2	109Mt+6d-1	110Ds+6d0	100Fm+5f1
92U-5f0	93Np-5f1	94Pu-5f2	95Am-5f3	96Cm+5f-3	97Bk+5f-2	98Cf+5f-1	99Es+5f0

|

Fig. 25.

19 Vers les tableaux présentés précédemment.

Entre autres les tableaux symétriques que j'ai publiés antérieurement, tels le tableau elliptique et le carré de carrés.

Par exemple, voici ce que devient la strate 4 mise à jour. J'ai

-|+

57 96

60Nd	59Pr	58Ce	57La	96Cm	97Bk	98Cf	99Es
61Pm	73Ta	72Hf	71Lu	108Hs	109Mt	110Ds	100Fm
62Sm	74W	82Pb	81Tl	116Lv	117Uus	111Rg	101Md
63Eu	75Re	83Bi	87Fr	120Ja	118Qb	112Cn	102No
95Am	107Bh	115Uup	119Uue	88Ra	86Rn	80Hg	70Yb
94Pu	106Sg	114Fl	113Uut	84Po	85At	79Au	69Tm
93Np	105Ha	104Rf	103Lr	76Os	77Ir	78Pt	68Er
92U	91Pa	90Th	89Ac	64Gd	65Tb	66Dy	67Ho

Fig. 26. La strate 4 dans le tableau elliptique du 1er novembre 2004.

20 Bidimensionnel B.

Le Tableau elliptique du 1er novembre 2004. L'ordre d'écriture équilibré.

Quelques idées pour continuer cette présentation. Un arbitraire, je commence en haut à gauche avc z=1. Les équerres sont insécables, je les écris dans le sens direct, celui des aiguilles d'une montre ou son inverse.

Un autre arbitraire, je commence les autres périodes le plus à droite possible avec le sens de rotation inverse, par exemple 5B pour le 2e période.

J'ai refait le Tableau elliptique du 1er novembre 2004 en cherchant de réaliser au maximum, dans l'ordre de lecture dans les équerres, l'alternance gauche droite et l'alternance du sens de rotation.

60Nd

59Pr

58Ce

57La

96Cm

97Bk

98Cf

99Es

23V

22Ti

21Sc

61Pm

73Ta

72Hf

71Lu

108Hs

109Mt

110Ds

100Fm

44Ru

45Rh

46Pd

6C

5B

24Cr

32Ge

31Ga

62Sm

74W

82Pb

81Tl

116Lv

117Uus

111Rg

101Md

52Te

53I

47Ag

16S

17Cl

1H

7N

11Na

25Mn

33As

37Rb

63Eu

75Re

83Bi

87Fr

120Ja

118Qb

112Cn

102No

56Ba

54Xe

48Cd

20Ca

18A

4Be

3Li

15P

19K

43Tc

51Sb

55Cs

95Am

107Bh

115Uup

119Uue

88Ra

86Rn

80Hg

70Yb

38Sr

36Kr

30Zn

12Mg

10Ne

2He

14Si

13Al

42Mo

50Sn

49In

94Pu

106Sg

114Fl

113Uut

84Po

85At

79Au

69Tm

34Se

35Br

29Cu

8O

9F

41Nb

40Zr

39Y

93Np

105Ha

104Rf

103Lr

76Os

77Ir

78Pt

68Er

26Fe

27Co

28Ni

92U

91Pa

90Th

89Ac

64Gd

65Tb

66Dy

67Ho

Fig. 27. Le tableau elliptique mis à jour 7X2014. Comme No 1 qui suit. Ce No 1contient des astérisques marquant les 19 éléments iréguliers

Ce tableau possède une colonne vertébrale.

60Nd

59Pr

*58Ce

*57La

*96Cm

97Bk

98Cf

99Es

Tableau

elliptique

No 1.

X2014

23V

22Ti

21Sc

61Pm

73Ta

72Hf

71Lu

108Hs

109Mt

110Ds

100Fm

*44Ru

*45Rh

*46Pd

* irrégulier

6C

5B

*24Cr

32Ge

31Ga

62Sm

74W

82Pb

81Tl

116Lv

117Uus

111Rg

101Md

52Te

53I

*47Ag

16S

17Cl

1H

7N

11Na

25Mn

33As

37Rb

63Eu

75Re

83Bi

87Fr

120Ja

118Qb

112Cn

102No

56Ba

54Xe

48Cd

20Ca

18A

4Be

3Li

15P

19K

43Tc

51Sb

55Cs

95Am

107Bh

115Uup

119Uue

88Ra

86Rn

80Hg

70Yb

38Sr

36Kr

30Zn

12Mg

10Ne

2He

14Si

13Al

*42Mo

50Sn

49In

94Pu

106Sg

114Fl

113Uut

84Po

85At

*79Au

69Tm

34Se

35Br

*29Cu

8O

9F

*41Nb

40Zr

39Y

*93Np

105Ha

104Rf

103Lr

76Os

77Ir

*78Pt

68Er

26Fe

27Co

28Ni

*92U

*91Pa

*90Th

*89Ac

*64Gd

65Tb

66Dy

67Ho

Ce tableau ne possède pas une colonne vertébrale.

60Nd

61Pm

62Sm

63Eu

102No

101Md

100Fm

99Es

Tableau

elliptique

No 2.

X2014

23V

*24Cr

25Mn

59Pr

73Ta

74W

75Re

112Cn

111Rg

110Ds

98Cf

48Cd

*47Ag

*46Pd

* irrégulier

6C

7N

22Ti

32Ge

33As

*58Ce

72Hf

82Pb

83Bi

118Qb

117Uus

109Mt

97Bk

54Xe

53I

*45Rh

18A

17Cl

1H

5B

11Na

21Sc

31Ga

37Rb

*57La

71Lu

81Tl

87Fr

120Ja

116Lv

108Hs

*96Cm

56Ba

52Te

*44Ru

20Ca

16S

4Be

3Li

13Al

19K

39Y

49In

55Cs

*89Ac

103Lr

113Uut

119Uue

88Ra

84Po

76Os

*64Gd

38Sr

34Se

26Fe

12Mg

8O

2He

14Si

15P

40Zr

50Sn

51Sb

*90Th

104Rf

114Fl

115Uup

86Rn

85At

77Ir

65Tb

36Kr

35Br

27Co

10Ne

9F

*41Nb

*42Mo

43Tc

*91Pa

105Ha

106Sg

107Bh

80Hg

*79Au

*78Pt

66Dy

30Zn

*29Cu

28Ni

*92U

*93Np

94Pu

95Am

70Yb

69Tm

68Er

67Ho

Fig. 27bis. Tableaux elliptiques No 1 et No 2. Seul le tableau No 1 possède une colonne vertébrale. J'appelle ainsi les 2 rangées les plus longues du No 1, dont aucun terme n'est irrégulier. 20 colonnes, 8 rangées, 160 cases dont 120 occupées. - Dans le No2, les deux rangées centrales renfement 4 éléments orréguliers

,ont

21 Remerciements et hommages à des prédécesseurs.

Merci à Maurice Day et à Patrick Demers pour leur aide.

Je dois beaucoup à Gilbert Lannoy qui m'a fait connaître Fernando Dufour dont l'oeuvre m'a inspiré au départ en 1995, à Guy-Robert Barthélémy, dont les travaux m'ont fait remarquer les propriétés du nombre 30, membre de la LISULF. Ausi bien que le célèbre Grothendieck, il publie ses résultats en français et en ligne. Et à un grand nombre de de penseurs et de savants à commencer par les Grecs de l'Antiquité, à Charles Janet, à Béguyer de Chancourtois et Mendeleev.

Il faut que je mentionne la contribution de Paul-Antoine Giguère à l'Université Laval à Québec, en particulier ce vitrail monumental qu'il lui a légué, oeuvre du vitrailliier Marius Plamondon.

. .

https://www2.ulaval.ca/fileadmin/ulaval_ca/gabarit/art-public/Volume_1_-_Art_public.pdf

L'art public sur le campus de l'Université Laval 83Comité d'aménagement et de mise en oeuvre (CAMEO)56 - Tableau périodique des éléments Giguère Plamondon Figure 101

Concepteurs:

Oeuvre: Marius Plamondon (Québec, 1914 - Montréal, 1976).

Type et code de l'oeuvre:

Vitrail - 8 unités (L.BAv.14).

Matériaux:

Verre.

Dimensions:

Longueur 8,80 mètres.

Description et signification:

Le vitrail présente la classification des éléments chimiques d'après la loi périodique de

Mendéléev et la configuration électronique des atomes

Fig. 28. ...Je souhaite que l'Université Laval en diffuse une représentation plus détaillée.

Ce vitrail m'a suggéré le surlignage de Fig. 15 ci-haut, et la possibilité de réaliser un vitrail à partir de cette figure, le vert est couleur d'espérance pour le Québec et couleur des Patriotes de 1837.

Cela m'a aussi rappelé un immense vitrail souvenir de mon enfance, oeuvre de Nincheri dans l'église Saint-Viateur à Outremont, dans le transept côté est. Fig. 29bis.

Et encore l'admirable petit livre intitulé Vitrail de la poëtesse et peintre Cécile Chabot que je rencontrais à la Côte-des-Neiges.

. .

Fig. 29. Vitrail de Cécile Chabot.

. .

Fig. 29 bis. Vitrail de Guido Nincheri, S. Viateur d'Outremont. Courtoisie Maurice Day. Le Congrès eucharistique de 1910, rappel du discours historique de Henri Bourassa.

22 Références.

Réf. 1. https://www.google.ca/search?q=atomes+cubiques+de+lewis&client=firefox-a&hs=Ave&rls=org.mozilla:fr:official&channel=fflb&tbm=isch&tbo=u&source=univ&sa=X&ei=SBEnVNH_GYKTyQT4wYHQBw&ved=0CDYQ7Ak&biw=1152&bih=746

atomes cubiques de G. N. Lewis.

Réf. 2.

http://fr.wikipedia.org/wiki/Crochet_%28typographie%29

Un crochet est un signe de ponctuation. Il peut être ouvrant (« [ ») ou fermant (« ] »). On dit un astérisque *.

Réf. 3. En modifiant l'ordre des éléments inscrits dans les crochets Fig. 15, sans changer le contenu de ceux -ci, j'expliquerais logiquement la création du tableau elliptique No 1, possédant une colonne vertébrale de 2 rangées horizontales; les 40 éléments inscrits dans ces rangées présentent une saturation des valeurs de m, quantum magnétique.

Réf. 4. Les exceptionnels ou irréguliers. Système du Québécium La nouvelle classification des éléments PUM 2004. Extrait d'une publication papier Pierre Demers PUM 2004 ISBN 2-9802454-0-2 page 48, La nouvelle classification des éléments.

. .

Fig. 30. Les irréguliers.

À suivre. 11X2014

- 30 -