Trentemagiquecommunsavoir2XII2012, http://www.lisulf.quebec/Trentemagiquecommunsavoir2XII2012.htm,

Système du Québécium.

Le nombre 30, nombre magique commun à plusieurs domaines du savoir.

Pierre Demers

Traduction interdite

3X2012*. Version du 17XII2012.

Sommaire. On appelle « nombres magiques » certaines suites d’entiers remarquables observées dans la nature, parce qu’elles jouent un rôle explicatif important par exemple en physique du noyau atomique : 2, 8, 20, 28, 50, 82 et 126, en art le nombre d’or et en phytomathématique les nombres de Fibonacci 1, 1, 2, 3, 5, 8... Des théories abstraites justifient leur intervention, celle des quanta ou celle de l’arithmétique. Procédant à l’inverse, je signale qu’en théorie mathématique abstraite 30 génère nécessairement des suites d’entiers remarquables douées de symétrie 4, je propose d’appeler 30 nombre magique. Il se trouve que 30 et ces entiers ont un rôle explicatif important dans plusieurs domaines du savoir: temps, calendriers, usages de l’humanité, architecture et urbanisme, mécanique, système du québécium comprenant structure atomique, code génétique et évolution biologique jusqu’au genre Homo. Dans un travail distinct, je présente à l’appui l’analyse d’une écriture cyclique des nombres premiers situés dans la base de numération 30. Réf. http://www.lisulf.quebec/quebecium.htm, Nos 1061, 1060, etc

Tel que soumis à l’ACFAS. Votre proposition de communication libre pour le 81^e Congrès de l'Acfas, intitulée Système du Québécium. Le nombre 30, nombre magique commun à plusieurs domaines du savoir. -2147 a été enregistrée avec succès. 28XI22012 15h13.

*Sous un titre différent.

Des nombres magiques dans le noyau atomique et ailleurs.

•a. En physique, Goeppert-Mayer et Jensen ont valorisé l’expression. Les nombres magiques des nucléons du noyau atomique sont 2, 8, 20, 28, 50, 82 et 126. Ils ont expliqué ces nombres dans une théorie quantique des spins et des moments cinétiques orbitaux des nucléons, par un couplage ls ou spin-orbite comme il en est connu en spectrosopie optique où ils s’appliquent aux électrons. Réfs 1, 2, 3, 4.

•b. En chimie, on appelle magiques les nombres d’atomes dans les agrégats d’atomes, distincts des cristaux et des molécules ordinaires. Dans le cas du sodium, ces nombres sont : 2, 8, 20, 40, 58 et 82. Ils sont interprétés dans une théorie des orbitales électroniques. Réf. 5.

•c. En chimie encore, on a appelé magiques, parmi les numéros atomiques z des éléments chimiques, ceux des gaz rares 2, 10, 18, 36, 54, 86 (et 118) terminant les périodes traditionnelles. Réf. 6.

•d. En beaux-arts, on appelle magique le nombre d’or ou de Fibonacci, encore appelé la divine proportion, égal à 1,618 033... Réf. 7.

•e. Les nombres de Fibonacci en biologie, végétale principalement. Ils forment en principe des suites illimitées, telle la suite 1, 1, 2, 3, 5, 8, 13, 21, 34… Ils génèrent le nombre d’or. Réf. 8, 9, 10

•f. En religions, ésotérisme, usages, jeux tels les carrés de Sudoku, des nombres très nombreux et des géométries, examinés scientifiquement, le carré alchimique, des univers magiques. Réfs 11, 12, 13.

•g. Ce qui n’a rien de numérique, une foule de publicités, vantant des moments magiques, des éclairages magiques etc. Il y eut la Lanterne magique du Chat noir en 1881 et les lanternes magiques que Descartes affectionnait. Réfs 14, 15, 16, 17, 18.

Dans tous ces cas de domaines, le qualificatif magique a une connotation historique et de surprise, suggérant, pour certains d‘entre eux, que les nombres proposés permettent de résoudre un problème jugé difficile à résoudre.

•h. Et puis, c’est le temps d’évoquer la magie des Rois qui approche, cette fête qui revient à tous les 6 de janvier, les Québécois fêtent l’Épiphanie catholique, ces Mages d’Orient étaient guidés par une étoile intriguante, venus à dos de chameau ou de dromadaires, Balthazar, Melchior et Gaspard apportèrent de l’or, de l’encens et de la myrrhe à Jésus nouveau-né, c’était l’An 0.

Description : Macintosh HD:Users:pierre:Desktop:images.jpg

Fig. 1.

(Noter quadrupèdes les montures). Merci Le Sourd. Réf. 19.

Discussion sur 30 et 4.

Ici, je propose d’appeler 30 et 4 nombres magiques, aussi bien que les nombres qui en découlent tels la suite 1, 4, 9, 16 et cette autre : 4, 16, 36, 64. L’aspect purement mathématique de ces nombres est discuté dans une publication distincte. Réf. 20.

On est conduit à dire que voilà des nombres magiques universels, disponibles pour s’appliquer à toute réalité numérisable : 30 concernant des dénombrenents et 4 des symétries. Ils ne semblent pas s’appliquer aux domaines a à h décrits plus haut. (Sauf h, où apparaît le transport à 4 pattes… Locomotion assistée: c’était par une monture quadrupède, avec mise en évidence du nombre magique 4 en l’an 0)

Mais voilà plusieurs autres domaines de connaissance, de A à H, où ils paraissent s’appliquer. Ils pourraient recevoir une interprétation quantique.

A. Mesure du temps. Horlogerie.

Par suite de conventions humaines inspirées de l’astronomie visuelle, qui se sont imposées au cours de l’histoire, trente s’applique exactement, après multiplication au besoin par des facteurs entiers simples 2 et 3 aux durées de la minute 60 secondes, de l’heure 60 minutes et du jour composé de 24 heures = 86400 sec. Pour des raisons astronomiques, il s’applique approximativement à l’année de 365,25 jours voisine de 360 jours et aux lunaisons de mois lunaire 29 jours 12 heures 44 minutes et 2,9 secondes voisines de 30 jours. L’écoulement du temps règle nos vies et l’activité de chacun. Pour le bonheur de l’industrie horlogère, chaque humain se doit de porter sa montre et de la consulter fréquemment, afin d’être à l’heure et à la minute. Voyez chaque jour, ville ou campagne, le flot de population laborieuse allant à son occupation quotidienne puis en revenant, usant de tous les moyens de transport régulièrement encombrés aux heures de pointe.

Trente se divise sans reste par 2, 3 et 6 ce qui donne lieu aux expressions quart-d’heure et 5 minutes. « Passer un mauvais quart-d’heure »; « le quart-d’heure académique », abrégé chez les germanophones en « m. z », « mit Zeit » ou « m. Z. » (avec temps), en latin « c. t. » (cum tempore, que les germaniques prononcent tsé té), pour signifier un retard admissible; à l’expression « encore 5 minutes », comme dans une anecdote relative à Saint Louis de Gonzague, utilisée par Françoise Loranger dans le titre d’une de ses pièces de théatre.

L’heure, son double valant 60 minutes, est divisible par 2, 3, 4, 6 et 12. (Le nombre 60, le nombre 12 permettent des fractionnements exacts commodes pour les commerces : une douzaine d’oeufs.)

Le morcellement sans reste par 30 de 60 minutes et par 15 de 60 minutes sont possibles mais guère usités.

Les essais de rationalisation décimaliste des durées sous la Révolution française eurent un succès temporaire. Le calendrier républicain ou révolutionnaire affirmait des mois uniformes de 30 jours divisés en décades, avec des sans-culottides, jours compensatoires en fin d’année. Il était anti-religieux, remplaçant les saints à souhaiter chaque jour par des noms de légumes et autres tirés de la nature et de la vie courante : potiron, plomb, violette, thon, pelle... Il dura de 1789 à 1815. Réf. 21.

Le calendrier révolutionnaire soviétique fut en vigueur en URSS de 1929 à 1940. Il affirmait lui aussi des mois de 30 jours, avec des jours compensatoires. Les semaines furent des pentades ou des hexades, de 5 ou 6 jours. Il était anti-religieux. Réf. 22.

B. Mesure des fréquences.

La fréquence est l’inverse d’un temps et a pour dimension temps^-1, son expression se fait en hertz Hz dont l’unité est la sec^-1. Ce qui est dit ci-avant au sujet du temps peut se répéter au sujet de la fréquence en Hz mutatis mutandis. Trente intervient donc dans l’expression de la fréquence de toute activité sociale; par exemple la parution du quotidien Le Devoir une fois par jour, la fréquence de cette de cette parution en Hz est 1/86400 = 86400^-1= 1,157.10^-5. La fréquence d’un anniversaire est 365 fois plus petite et vaut 1,157.10^-5/365 = 1/35186000 = 2,842.10^-8Hz. La fréquence d’un battement du cœur est un peu inférieure à 1Hz. Les sons audibles vont de 14 à 10⁴ Hz environ. La fréquence du courant alternatif d’Hydro-Québec est très exactement 60 Hz, 60 étant 2 fois trente. Naguère on disait « Aetas hominis septuaginta annos », l’homme vit 70 ans; de nos jours, il faudrait plutôt dire, cent ans.

La fréquence d’un décès devient alors le centième de celle d’un anniversaire, soit.

2,842.10^-8Hz/100

2,842.10^-10Hz.

Elle est minuscule mais non négligeable. Mais peut-on parler d’une fréquence pour un phénomène non-répétitif?

Restriction : il faut dire que le nombre trente comme tel ne se manifeste pas de façon aussi évidente dans notre appréciation humaine des fréquences que dans celle des durées, quand on jette un coup d’œil sur un cadran muni de ses 3 aiguilles, avec ses demi-heures et ses demi-minutes. Lorsqu’on surveille le soleil ou la lune ou une étoile se défiler entre les branches d’un arbre.

C. Mesure des vitesses et des accélérations. Mécanique.

vitesse = longueur.temps^-1, accélération = longueur.temps^-2; restrictions comme ci-avant.

D. Mesure des angles. Rotations. Géométrie appliquée.

Encore une fois par suite de conventions humaines, et très explicitement, trente est à la base de la division exacte du cercle en 360 degrés puis du degré en 60 minutes d’arc et de la minute d’arc en 60 secondes d’arc. On pourrait ajouter ici des considérations sur les vitesses angulaires de dimension angle. temps^-1; restrictions comme ci-avant.

E. Arpentage, architecture, génie civil, urbanisme.

Tous sont fondés sur une rose des vents avec 4 fois le triple de 30^o.

Trente est encore un nombre figuré tétra-octaédrique, l’octaèdre mis en cause étant le tétraèdre tronqué. Ces octaèdres s’associent de façon jointive pour donner des formes s’inscrivant dans un tétraèdre, en nombres 1, 5, 14, 30. 30 est le 4^e nombre tétra-octaédrique. recreomath tronque tetraedre

D Trente est encore un nombre figuré par l’association de son double 60 au 60-gone, polygone régulier de 60 cotés occupant 5 degrés chacun, ce qui s’inscrit dans un cercle : c’est le cadran horaire normal, famuiwr sur la place publique et dans l’ameublement..

E. Trente est la base d’un système de numération à la place de 10. On pourrait dès lors écrire la durée d’une heure exprimée en minutes, avec des conventions faciles.

une heure = 2 X 30 min = 02.00 min

Avec 02. pour 2 fois la demi-heure.

Et un jour de 24 h.

un jour = 48 demi-heures = 01.18.00 min

F.Vie urbaine.

.Il n’y a pas de vie urbaine possible sans les indispensables véhicules automobiles personnels. Ceux-ci font largement appel au nombre 4 pour 4 roues symétriquement placées; l’expression 4X4 est bien connue. Le genre Homo aux lointains ancêtres quadrupèdes est devenu bipède dans son domicile, mais s’il sort.en ville, il ne marche pas à 4 pattes, il circule en mettant en évidence le nombre magique 4. Fig. 2.

Description : Macintosh HD:Users:pierre:Desktop:Capture d’écran 2012-12-17 à 09.03.22.png

Fig. 2. Le 17XII2012 à Montréal. Merci QMI.

Quadri-roues en 2012 A. D., quadrupèdes en l’an 0: l’assistance à la locomotion recourt d’une façon qui a persisté à travers les siècles, au nombre magique 4. Voyez Fig. 1.

F. Suite du Québécium, nombres magiques 30 et 4.

Dans cette suite numérique, les nombres de 1 à 120 sont associés en 30 tétrades de 4. La suite du québécium figurée par un assemblage pyramidal de 30 tétraèdres tronqués. Réf. 23. Fig. 3 tirée de Réf. 24, Fig. 8.

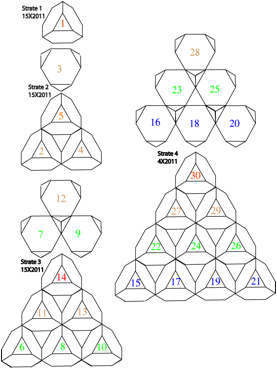
Fig. 3. La suite du québécium figurée par un assemblage pyramidal de 30 tétraèdres tronqués, vus dans la strate 4 une petite ou une grande face sur la table. La figure montre 7 pièces s’assemblant jointivement. Chaque tétraèdre tronqué peut figurer 4 éléments chimiques. De symétrie 4 comme le tétraèdre régulier. Tirée de Réf. 24, Fig. 8.

Références.

Réf. 1. Maria Goeppert-Mayer

Réf. 2. Hans Daniel Jensen

Réf. 3. Weizsäcker, Nombres magiques en physique du noyau, http://fr.wikipedia.org/wiki/Nombre_magique_%28physique%29,

La version anglaise est plus complète.

Réf. 4. Guedira, Couplage spin-orbite,

cours.polymtl.ca, GUEDIRA

Réf. 5 Jean Farges, Agrégats,

Nombre magique chimie

Réf. 6. David Verney, « En physique atomique les nombres magiques d’électrons correspondent aux gaz nobles hélium (2 électrons de valence), néon (10), argon (18), krypton (36), xénon (54) et radon (86) qui sont immuables et inscrits pour l’éternité en bout de ligne du tableau des éléments de Mendéléiev. «

structure couches in2p3

Réf. 7. Craponne, Le nombre d’or,

trucsmaths free

Réf. 8. Roger Jean, Phytomathématique Roger V. Jean, PUQ, 1978. ISBN, 0777002329, 9780777002322.

puq, roger jean

Réf. 9. Roger Jean, Croissance végétale et morphogénèse

Réf. 10. Charles-Émile Jean, Dictionnaire de mathématiques récréatives ,

recreomath qc fibonacci

Réf. 11. Guillaume Yoda, Nombres - Curiosités, théorie et usages,

yoda guillaume pages perso orange,

Réf. 12. Marie-Claire Lagacé, …des univers magiques avec Moment Factory, sur la toile, cherchez « Les diplômés magazine », », No 423, automne 2012, page 14.

Réf. 13. Yvan Saint-Pierre 2012, sur la toile, cherchez « Les diplômés magazine », No 423, automne 2012, page 50.

http://www.amazon.com/Le-carr%C3%A9-alchimique-French-Edition/dp/1466269693,

Réf. 14. Henri Rivière, Le Chat Noir 1881,

wiki Le Chat noir Apparitions«… Caran d'Ache. Il créa également, avec l'aide d'Henri Rivière, un théâtre d'ombres en couleurs…

Réf. 15. Jac Remise,

Magie lumineuse du théatre d'ombres à la lanterne magique ...

www.lepuitsauxlivres.com › Catalogue › Objets › Photo-Ciné

Magie lumineuse du théatre d'ombres à la lanterne magique - Remise Jac ... De la chambre noire à la lanterne magique 18 ... L'épopée du Chat-Noir 303

http://www.alienor.org/articles/chat_noir/engouement.htm

Réf. 16. Comte de Paroy, lanternes magiques,

ac-nancy-metz.fr/cinemav,

“… ce moyen d’éducation se propagerait de la Chine au Canada.”

Réf. 17. Édouard Cornely, http://diaprojection.unblog.fr/2012/03/08/la-lanterne-magique-dans-les-cabinets-de-physique/

Réf. 18. René Descartes, il invente la lanterne magique.

http://books.google.ca/books?id=LQ4hwJPYdoIC&pg=PA78&lpg=PA78&dq=descartes+sa+lanterne+magique&source=bl&ots=8w9BZ_QbmR&sig=9S3KnMasULS6kexzfREkhnIfW8k&hl=fr&sa=X&ei=bLDOUJ_HLYGm8QTF94H4CQ&redir_esc=y - v=onepage&q=descartes sa lanterne magique&f=falsh

Description : Description : Description : Macintosh HD:Users:pierre:Desktop:Capture d’écran 2012-12-17 à 00.47.16.png