Unoctaedrebis10IV2008

Système du Québécium.

Un octaèdre pavant et son usage dans un tableau 3D des éléments chimiques.

Pierre Demers

Sommaire. L'octaèdre que j'étudie est le tétraèdre tronqué d'Archimède. Il possède 4 faces hexagones réguliers et 4 faces triangles équilatères. Il se prête à paver l'espace 3D. On obtient aisément cet octaèdre creux par troncature du tétraèdre régulier creux et alors il n'a que les 4 faces hexagones, les faces triangles étant des fenêtres. Il permet de figurer une tétrade d'éléments, un élément pour chaque face hexagone. En associant 30 de ces octaèdres jointivement, je réalise un tableau 3D des 120 éléments dessinant un tétraèdre régulier, dans lequel il est possible de lire de l'extérieur le nom de chaque élément. Références : heptaèdre, hexaèdre, pentaèdre obtenus semblablement.

 

Introduction

Le présent travail continue celui 967 de 2005, dont les figures 3 et 4 montrent des patrons triangulaires de tétraèdres, composés d'un triangle central entouré de 3 triangles extérieurs. 967 http://www.lisulf.quebec/Atomesentetradeshtml

 

Patron triangulaire. Figuration 3D d'une tétrade.

Un triangle équilatéral peut se décomposer en 4 triangles équilatéraux égaux. Par pliage selon 3 lignes, un grand triangle peut être replié 3 fois pour donner un tétraèdre creux fermé ou un aspect godet. Par 2 replis, il peut prendre l'aspect d'un escarpin, deux faces se rejoignant. Fig. 1.

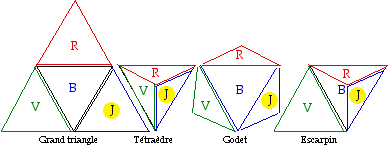
Fig. 1.  Un grand triangle et ses transformations par pliage. Le code coloré diffère selon les figures. OctaFig1.gif

 

À chacun des 4 triangles, est attribué le nom d'un élément d'une tétrade. Ainsi, on peut affecter un patron à chacune des 30 tétrades des éléments. Cette intention, présentée, comme exploratoire en 2005, est ici réalisée pour les 5 premières tétrades allant de z = 1 à z = 20, de H  à Ca, dans les formes 3D godet et escarpin, fig. 2, fig,3.

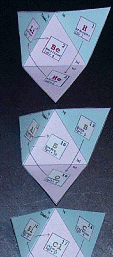
Fig. 2. Godets. OctaFig2a.gif, OctaFig2b.gif, OctaFig2c.gif, OctaFig2d.gif

 

Fig. 3. Escarpins. Cinq tétrades, la rangée supérieure d'une tétrade constitue la strate 1, la rangée inférieure de 4 tétrades, la strate 2. Il faudrait ensuite une rangée de 9 tétrades pour la strate 3 et une de 16 tétrades pour la strate 4. OctaFig3.gif Mais voyez la figure suivante.

 

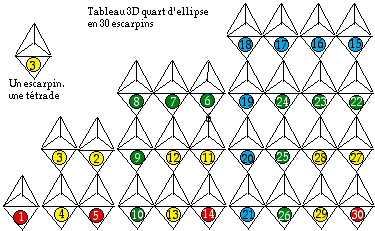
Fig. 4. Tableau 3D  quart d'ellipse des 120 éléments en 30 escarpins. Poursuivant l'exploration, je dispose les 30 escarpins à la manière de la figure 6 Atofig6b.gif du travail de 2005, soit en quart d'ellipse. Chaque escarpin porte ici le numéro d'une tétrade, comme dans  le Tableau quart d'ellipse, gqafig15,54aquartd.gif, dans http://www.lisulf.quebec/gqajuin2.htm

http://www.lisulf.quebec/Atomesentetradeshtml

OctaFig4.gif

 

Troncatures.

Octaèdre.

Dans le grand triangle de la figure 1, on remplace chacun des 4 triangles composants par l'hexagone régulier inscrit. Un triple repli donne alors un tétraèdre quatre fois tronqué. L'arête est le tiers de celle du tétraèdre original. Le tétraèdre tronqué obtenu est creux, il a 4 faces hexagones et délimite 4 faces fenêtres vides triangles équilatères. Les arêtes des faces hexagones et triangles sont égales, valant chacune le tiers de l'arête du tétraèdre original. La figure obtenue a 8 faces et est un octaèdre non régulier. Une autre manière d'obtenir cet octaèdre est de raccourcir symétriquement au tiers chaque arête d'un tétraèdre régulier.. Fig. 5. Cet octaèdre s'inscrit dans un tétraèdre qui le circonscrit de 2 façons : par ses faces octaèdres, ce qui résulte de la construction décrite; et par ses faces triangles, et alors le tétraèdre circonscrit est d'arête double de celle du tétraèdre circonscrit précédent. On peut encore dire que l'octaèdre décrit est l'intesection de 2 tétraèdres réguliers dont les arêtes sont dans le rapport 1 à 2.

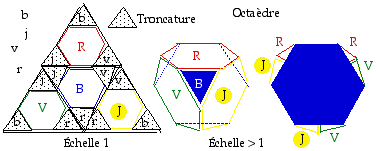
Fig. 5. Par troncature d'un tétraèdre régulier sur chacun de ses 4 sommets bvjr, on obtient un octaèdre ayant 4 faces hexagones et 18 arêtes égales. Il a en outre 4 faces triangles équilatères qui sont des fenêtres. Vues : une face triangle b en haut, puis en bas. Les sommets tronqués et les faces triangles résultantes sont désignés par les lettres minuscules des capitales désignant les faces opposées.

 

Heptaèdre.

Fig. 6. Comme la figure précédente, mais troncature appliquée à 3 sommets d seulement. On obtient un heptaèdre ayant 3 faces fenêtres. Cet heptaèdre a un plan de symétrie perpendiculaire aux faces R et B..

 

Hexaèdre.

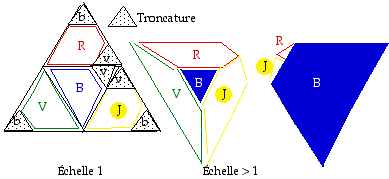
Fig. 7. Troncature appliquée à 2 sommets seulement. On obtient un hexaèdre ayant 2 faces fenêtres. Cet hexaèdre a un plan de symétrie perpendiculaire au plans V et B.

Pentaèdre.

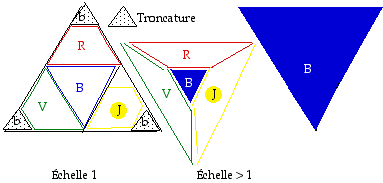
Fig. 8. Troncature appliquée à un seul sommet. On obtient un pentaèdre ayant une face fenêtre. Ce pentaèdre a un axe de symétrie ternaire centré sur la face B et 6 plans de symétrie passant par cet axe.

 

pavage 3D par l'octaèdre.

Dans l'utilisation que je décris, un octaèdre est affecté à chacune des tétrades d'éléments et chaque face hexagonae d'un octaèdre porte le nom de l'un des éléments de la tétrade. Les octaèdres décrits ont la propriété de s'associer jointivement pour paver l'espace 3D, en déterminant des pyramides tétraédriques.

 

Ils ne pavent pas l'espace à eux seuls comme le font les rhombododécaédres ou les cubes. Il faut les accompagner de tétraèdres de même arête appliqués à leurs faces fenêtres, ces tétraèdres pouvant être imaginés ou sous-entendus. Chaque fois qu'un tétraèdre est requis, au moins 3 de ses arêtes sont en commun avec celles d'une fenêtre d'un octaèdre. Un tétraèdre a 6 arêtes.

Fig. 9. Dans un octaèdre, les 4 fenêtres triangles rjvb.

 

Pour s'appliquer l'un sur l'autre, 2 octaèdres doivent être tête-bèche comme ceux de la figure 9 et l'un d'eux doit effectuer une rotation de 60o, puis une translation horizontale. C'est à la différence de deux cubes, qui, figurés tête-bèche côte-à-côte, s'appliquent l'un sur l'autre par translation horizontale aussi, mais sans rotation. D'ailleurs, pour des cubes, tête-bèche ne se discerne pas d'identique.

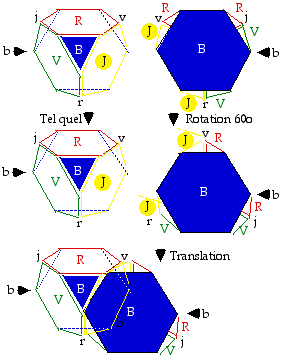
Fig. 10. Application d'un octaèdre sur un autre par la face jaune..

Fig. 11. Quatre octaèdres associés définissent un tronc tétraédrique que six tétraèdres complémentaires complèteraient, numérotés t1 à t6. OctaFig11.gif

 

Fig. 12. Vue de quatre octaèdres associés. OctaFig12.gif

 

Fig. 13. Vue de 5 octaèdres associés. Ils définissent un tétraédre que dix tétraèdres complèmentaires complèteraient.OctaFig13.gif

Hublots.

Une fenêtre, par exemple circulaire comme un hublot, pratiquée dans chaque face hexagonale d'un octaèdre, facilite l'inspection intérieure de cet octaèdre et celle des octaèdres voisins. Présentement, je manque d'un emporte-pièce qui faciliterait l'opération nécessaire sur la feuille imprimée. J'utilise du papier et du carton mince et je colle arête sur arête.

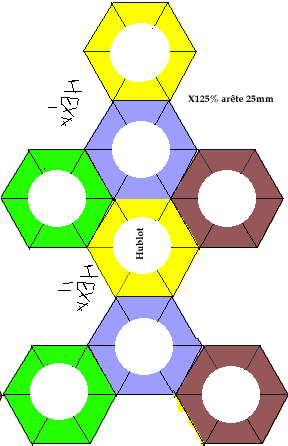
Fig. 14. Patron donnant 2 octaèdres avec hublots. OctaFig14.gif

 

Strates. Tableau 3D.

Les strates peuvent maintenant se figurer par des agencements d'octaèdres représentant chacun une tétrade. L'ordre à l'intérieur d'une tétrade est RJVB, H1, He2, Li3, Be4 dans la 1re strate, N7, Ne10, P 15 , A18 etc. Il est donné figs 2 et 3. Les agencements sont jointifs et pavants (on suppose les octaèdres complétés par les tétraèdres complémentaires). L'agencement global dessine un tableau 3D qui est un grand tétraèdre ayant à ses 4 sommets autant de tétraèdres complémentaires, ayant 4 niveaux. Les niveaux sont numérotés à partir de 1 pour le niveau supérieur. Un niveau par strate. Fig. 15.

Strate 1 : un octaèdre, tétrade 1, 4 tétraèdres complémentaires.

Strate 2 : 4 octaèdres,tétrades 2 à 5, 6 tétraèdres complémentaires.

Strate 3 : 9 octaèdres, tétrades 6 à 14 9 tétraèdres complémentaires.

Strate 4 : 16 octaèdres, tétrades 15 à 30, 14 tétraèdres complémentaires.

 

Le contenu des équerres du tableau 2D quart d'ellipse déterminant les nombres de cases 1, 3, 5, 7 se transpose dans les strates du présent tableau 3D, une équerre correspondant à une rangée. Des considérations de symétrie pourraient suggérer un agencement différent, mais ici j'ai choisi une transposition dans l'ordre numérique. De la sorte, il se trouve que la colonne vertébrale occupe la face à droite dans la figure, soit les cases 1, 3, 5, 10, 13, 14, 21, 26, 29 et 30.

Fig. 15. Tableau 3D en tétrades octaèdres quart d'ellipse des éléments chimiques. Les nombres manuscrits sont les numéros d'ordre des tétrades. Chaque face limitant le tableau est formée de 10 hexagones. La colonne vertébrale forme la face à droite. OctaFig15.gif

 

Heptaèdres, hexaèdres, pentaèdres et tétraèdres.

De toute évidence, on peut remplacer par des tétraèdres, les 4 octaèdres aux sommets du tableau 3D. Ces tétraèdres ont une arête valant 3, l'unité étant l'arête de l'octaèdre. On peut remplacer certains octaèdres par des heptaèdres, des hexaèdres ou des pentaèdres. Les nombres de tétraèdres complémentaires requis sont modifiés en conséquence. Fig. 16.

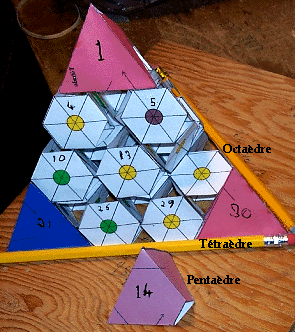
Fig. 16. Modification de la figure précédente. Tableau 3D en tétrades quart d'ellipse, octaèdres, tétraèdres, un  pentaèdre. La place du pentaèdre est vide. OctaFig16.gif

 

 

Conclusions et perspectives.

Ma première conclusion est géométrique. Le présent travail attire l'attention sur des formes rarement examinées, ayant 5, 6, 7 ou 8 faces et dérivées du tétraèdre régulier. Notre pentaèdre n'est pas une pyramide quadrangulaire, notre hexaèdre n'est pas un cube. Notre octaèdre n'est pas l'octaèdre régulier; il est l'un des 13 solides d'Archimède, connu sous le nomm de tétraèdre tronqué.

Ma deuxième conclusion est davantage physique. Je présente une classification des éléments chimiques en 3 dimensions, dans une solution remarquable par ses symétries qui, encore une fois dans le système du québécium sont d'ordre 4 et associées à celles du spin de l'électron.

Troisième conclusion :  tout objet 3D est encombrant et si l'on tient à représenter la classification des éléments chimiques en 3 dimensions, l'objet aux dernières figures ci-dessus, plus ou moins transformé, pourrait-il devenir pratique et d'utilité courante, le nom de chaque élément étant bien lisible? Après tout, les globes terrestres ont leurs qualités distinctives et on en fabrique encore malgré la commodité des planisphères faciles à ranger. L'objet pourrait se déployer en 4 strates grâce à des charnières.

Quatrièmement : sur la base des dernières figures encore, on pourrait créer un jeu d'assemblage. Les cubes de Rubik ont eu un succès persistant.

-30-