gqajuin2.doc.w5.1
Précédent gqajuin1.html Suivant à venir
Traduction interdite Tous droits de traduction réservés
Système du Québécium
Nombres et géométrie
dans la classification des éléments.
1 sur 2. Suite et fin.
Pierre Demers.
1/2 Première partie. Suite.
Tableau quart d'ellipse

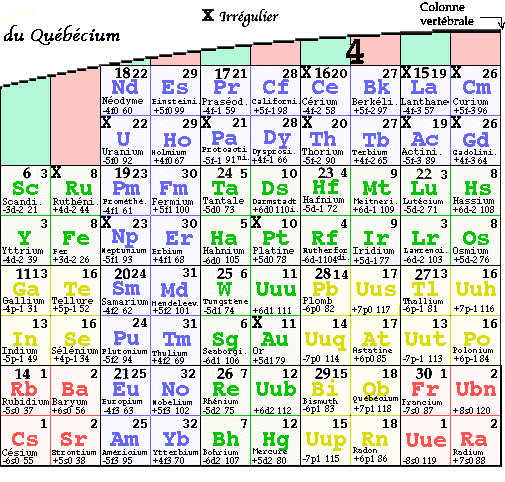
Fig. 15, 54. Tableau quart d'ellipse, Il contient cent vingt éléments en trente tétrades. Les tétrades sont repérées par leur numéro allant de 1 à 30 et par le premier élément écrit dans leur grande case en position NO. Ainsi numéro 25 W 74.. Une tétrade renferme deux orbitales. - La colonne vertébrale comprend la rangée inférieure de dix tétrades ou quarante éléments
Atomes réguliers, atomes irréguliers.
Une théorie atomique semi-empirique basée sur la succession des niveaux de l'atome d'hydrogène a permis d'établir par convention, une liste unidimensionnlle des atomes par valeurs de Z qui fait pratiquement l'unanimité des chimistes et des physiciens. Cette liste contient, dans l'ordre des valeurs de Z, le caractère de chaque électron constituant. Voyez la formule du québécium. Fig. 3, 71.
La formule électronique d'un atome Z peut s'y lire en commençant à gauche et en arrêtant au numéro égal à Z. C'est la formule idéale, régulière ou nominale de cet atome. Tout atome a sa formule nominale uniquement définie. Il occupe une case Z, par exemple dans le tableau Fig. 3, 51ter où l'on inscrit son caractère c'est-à-dire le caractère de son électron de valence. Sa formule comprend celle de son coeur, c'est-à-dire le contenu des cases précédentes, en plus de son caractère propre. Ces conventions permettent d'établir des tableaux pratiques des éléments sans illogisme.
L'expérience a montré que la formule nominale de 19 éléments appelés irréguliers, ne coïncide pas avec la formule réelle, laquelle ne répond pas à à la règle de lecture ci-haut, le coeur et l'électron de valence réels diffèrent des valeurs régulières. Pour ces atomes, si on inscrivait dans la case Z le caractère vrai de l'électron de valence, il y aurait illogisme car il faudrait récrire la composition du coeur, ce qui rendrait le tableau faux pour certains éléments.
Atomes réguliers. La colonne vertébrale du tableau quart d'ellipse. L'expérience démontre que les dix grandes cases, formant la rangée inférieure du tableau en tétrades, ne renferment que des atomes réguliers. C'est la colonne vertébrale du tableau, qui renferment. tous les éléments dont toutes les sous-couches sont complètes. Fig. 15, 54.
Une autre catégorie d'atomes réguliers est celle des trente atomes s et p, dont vingt-quatre sont situés en dehors de la colonne vertébrale. Au total la colonne vertébrale "élargie" est formée de soixante-quatre éléments. Les éléments hors la colonne vertébrale sont au nombre de cinquante-six et sont le domaine des irréguliers. Ce sont exclusivement des éléments d et f.

Fig. 16, 12. Colonne vertébrale de quarante éléments dans le Tableau quart d'ellipse. La colonne vertébrale élargie comprend en outre vingt-quatre atomes p, soit au total soixante-quatre.
Atomes irréguliers. On en connaît dix-neuf, qu'on peut repérer sur le Tableau elliptique Fig. 14, 53. On reconnaît qu'ils sont exclusivement d ou f, aucun élément s ou p n'étant irrégulier. Leur disposition, à première vue ne présente pas de régularité apparente. La plupart des auteurs leur accordent peu d'attention et ils constituent un inconvénient pédagogique. Je n'ai pas pu trouver une théorie satisfaisante les expliquant. Un caractère commun à tous les atomes irréguliers est que leur formule, telle que pointée sur la liste Fig. 2, 71, comporte des lacunes.
http://www.lisulf.quebec/QbSyst2e.23quater.html "Les exceptions".*
*Une manière de signaler le caractère exceptionnel d'un atome consiste à faire suivre son symbole de deux nombres, l'un égal à z nombre d'électrons qu'il renferme et l'autre égal au numéro d'électron le plus élevé qu'il renferme. L'électron manquant ou lacunaire est mentionné entre parenthèses. Ainsi Cr24, 25. Sa formule complète serait Cr24, 25 (non 20)."
Régularités dans la disposition des atomes irréguliers. Ils sont aussi repérés sur le Tableau quart d'ellipse. On voit qu'ils sont compris dans onze tétrades. Leur présentation en tétrades révêle une sorte de régularité à laquelle ils obéissent. Voici la suite des onze tétrades qui contiennent des éléments irréguliers, ordonnées selon la valeur de leur désignation Z. Fig. 17.

Fig, 17irr. Dix-neuf éléments irréguliers présentés par tétrades. Seules sont figurées les onze tétrades renfermant des atomes irréguliers. L'utilisation des tétrades et du Tableau quart d'ellipse permet d'apercevoir une sorte de régularité dans la répartition des atomes irréguliers selon le numéro de la tétrade. Cette répartition est unimodale et elle est dispersée de la tétrade six du scandium jusqu'à la tétrade vingt-cinq du tungstène, elle passe par un maximum unimodal caractérisé étalé sur les deux tétrades neuf du chrome et quinze du lanthane. - En se bornant aux tétrades figurées : le maximum des irrégularités se situe à la fin de la strate trois et au début de la strate quatre.
Le processus d'analyse utilisé, basé sur l'emploi des tétrades pour classifier les éléments, fait apparaître des régularités dans la fréquence d'apparition d'éléments irréguliers dans une tétrade. Cette fréquence peut valoir zéro, un, deux, trois ou quatre. Les tétrades de fréquence zéro sont omises de la liste et on n'aperçit pas de fréquence trois. Ces apparitions répondent à l'apparition des séries de nombres quatre, deux, un en sens inverse dans la strate trois et en sens direct dans la strate quatre. Dans la strate quatre, il se trouve trois apparitions de la fréquence un en plus. Les séries complètes sont comme au Tableau suivant. On n'a pas observé la fréquence trois.
Le Tableau qui suit résume ce qui précède sur les éléments irréguliers.
Tableau
Éléments irréguliers. Fréquence de leurs apparitions dans une tétrade
Tétrades par valeurs croissantes de Z
Strate 3.........1 1 2 4............
Strate 3.........4 2 1 1 1 1 1
Il y a là une symétrie miroir remarquable dans les fréquences d'apparition des éléments, qui apparaît grâce au groupement des éléments par tétrade. Elle n'apparaît nullement dans la liste des éléments par valeur de Z. Sa manifestation est attribuable à l'intervention de symétries d'ordre quatre. En d'autres termes, l'usage des symétries quatre dans la classification des éléments paraît être plus qu'un artifice de calcul mais bien correspondre à la nature des forces entre électrons et noyaux.
Plus ample analyse de cette symétrie des éléments irréguliers toucherait les différences entre formules nominales et réelles.
La coupure 4s/3d
Après l'argon 18 qui est +3p1, la comparaison classique avec les niveaux de l'hydrogène suggère que l'élément suivant 19 devrait être -3d-2. Or le 19 est le -4s0. le potassium. Le niveau atomique -3d-2 appliqué au 19e électron aurait évidemment une énergie supérieure au niveau -4s0 et ne peut pas, pour cette raison, caractériser l'élément 19.
Le problème ne se pose pas dans le tableau par strates et par équerres du système du québécium. La construction Aufbau se fait par un processus topologique dans un espace virtuel ayant l'aspect de grilles indéfiniment étendues et où la premère occupation par des équerres définit l'espace limité d'une strate. L'occupation se poursuit dans l'espace disponible, par des équerres de dimensions adaptées à l'espace disponible. Or justement, une fois l'élément 18 qui est +3p1 est installé dans la strate 2, il ne reste que 2 places. Et un bloc d'éléments, qu'il soit s, p, d ou f, ne se brise pas. Soit il se case tout entier dans une strate soit il colonise l'espace indéfini des grilles virtuelles. Mais cette colonisation, qui est la création d'une strate nouvelle, est interdite tant que la strate précédente n'est pas pleine.
Le bloc d ayant 5 éléments - et 5 éléments +, ne peut pas se briser pour occuper 1 ou 2 cases seulement qui restent disponibles de la strate 2. Il faut trouver pied à la chaussure puisqu'on ne peut pas ajuster la chaussure au pied!
Le pied voulu est évidemment composé de 2 éléments d'une paire suivante, soit -3s0 et +3s0.
On peut suivre ce raisonnement éminemment stérique à la figure 6, strate 2, fichier 23bishtml du disque accompagnant mon livre de 2004.

Fig. 18,4s Extrait de mon livre de 2004 avec correction.
Le problème de la coupure 4s/3d est longuement discuté par Scerri qui critique Atkins.
Tableau de Kibler
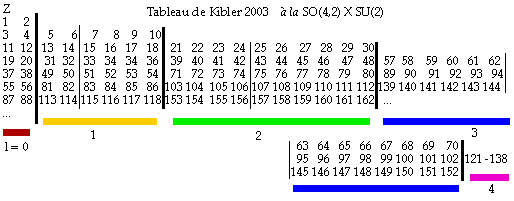
Fig.19, 67. Tableau 1 de Kibler (2003) réécrit.
Kibler présente un tableau (Tableau 1) qui a l'intérêt d'être inspiré par la théorie des groupes SO(4,2) et SU(2)l. Fig. 19, 67. Il ne le présente cependant pas comme étant le seul que la théorie des groupes pourrait inspirer. Un caractère intriguant de son tableau est la fragmentation des sous-blocs l = 1, 2 et 3 en fragments de sous-blocs inégaux, contenant l'un et l'autre un nombre pair de termes. Il les aligne linéairement. Le fragment court est entièrement de spin -. Le premier terme du fragment long est de spin - et les suivants, de spin +. Le fragment long est donc de spin hétérogène. Les rangées horizontales augmentent de longueur à chaque alinéa, ce qu'il obtient par des translations et par l'introduction de plusieurs éléments spéculatifs. L'accroissement de longueur des rangées est de quatre termes à chaque ligne nouvelle. La dualité de longueurs dans la Tableau périodique n'apparaît pas ici.
Les longueurs des rangées L sont évaluées en nombres de termes présents. Le Tableau 1 ressemble à cet égard au Tableau périodique Fig. 1.51ter avec ses régularités. Voici le relevé de ce dernier et de celui de Kibler
Périodique L =
2
8
8
18
18
32
32
2
Kibler L =
2
8
18
32
50
...
...
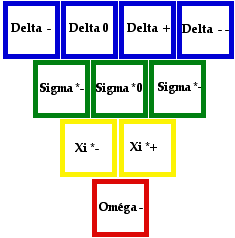
Fig. 20, 56. La théorie des groupes SU(3) a conduit à certains tableaux d'une symétrie évidente. Ici l'exemple de son application à la classification des particules du décuplet de baryons de spin-parité J = 3/2+. Les symétries triangulaires sont évidentes. Un tel tableau (la case ici en rouge étant aors vide) a conduit à la découverte de la particule oméga. Réf. Gell-Mann, Kibler p. 318.
Yves Schutz http://www-subatech.in2p3.fr/~photons/subatech/physics/collisionneurs/node11.html
Dans les deux cas, les quatre nombres 2, 8, 18, 32 sont présents, les nombres 8, 18 et 32 étant répétés dans le tableau périodique, non dans celui de Kibler.
J'aperçois aux cinq premières rangées du Tableau 1 de Kibler qui en comporte huit, une forme de régularité intéressante, basée sur le nombre quatre, dans la progression de la longueur des lignes, mais aucune apparence de symétrie d'ensemble particulière, d'ordre quatre ou autre, ce qui est à la différence de certains tableaux inspirés eux aussi par la théorie des groupes et qui ont conduit à des découvertes notoires. Fig. 20, 56.
Mise en équerres du Tableau 1
Convenons que les rangées de Kibler soient écrites dans deux dimensions, et que la partie courte (entièrement de spin -) soit écrite selon y à la manière d'une colonne selon y et la partie longue, selon x.. Alors nous avons le nécessaire pour obtenir une équerre, Voici le nombre de cases x et y selon la valeur de l.
l = 0, x = 2, y = 0
l = 1, x = 4, y = 2
l = 2, x = 6, y = 4,
l = 3, x = 8, y = 6
J'ai mis en équerres une partie du Tableau 1. Fig. 21, 57. Les équerres de rangées successives se prêtent à former des couronnes, ce qui est montré Fig. 22, 58.
Voyez Rouvray et King 2004, The Periodic Table : Into the 21st Century, ISBN 0-86380-292-3
www.research-studies-press.co.uk
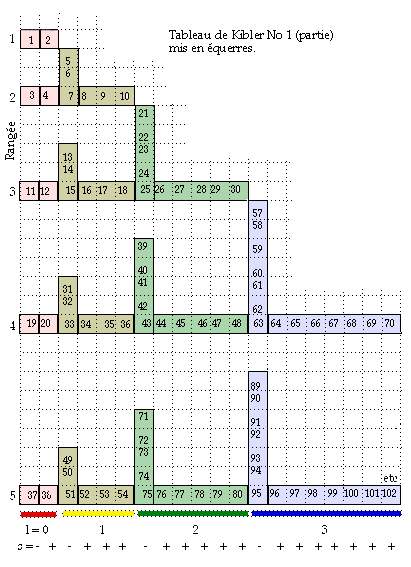
Fig. 21, 57. Mise en équerres d'une partie du Tableau 1 de Kibler. Telles quelles, ces équerres non équilatères ne démontrent pas une symétrie d'ordre quatre, mais elles la démontrent lorsqu'on ls associe deux à deux entre rangées successives. Voyez la figure suivante.
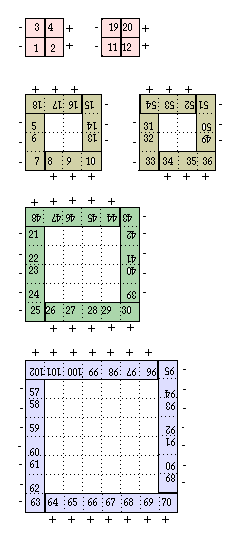
Fig. 22, 58. Couronnes résultant de la mise en équerres d'une partie du Tableau 1 de Kibler. Ces couronnes carrées manifestent une symétrie d'ordre 4 liée aux dégénérescences impaires dans les blocs. Les impairs impliqués sont 1, 3, 5, 7 pour les moments orbitaux 0, 1, 2, 3 respectivement. Le contenu du Tableau 1 ne permet pas de mettre en couronnes la totalité des 120 éléments.
Couplages j dans le Tableau 1 de Kibler
Kibler explique un peu de l'organisation de son Tableau 1 Fig. 19, 67, dans une publication distincte. Il utilise le paramètre j somme vectorielle de l et s. Ce paramètre étant impair donne une dégénérescence paire égale à 2, 4, 6, 8. Chaque sous-couche est de la sorte divisée en deux fragments pairs et inégaux, ce qui ne favorise pas le repérage des orbitales. En utilisant ce procédé, on ne change pas le nombre d'éléments présents dans sous-couche, égal à deux fois un impair.
On se prive d'afficher des nombres impairs. On se prive d'afficher, dans chaque sous-couche, des fragments égaux contribuant à la symétrie de l'ensemble.http://monsite.wanadoo.fr/Maurice_Kibler/index.jhtml
http://spiral.univ-lyon1.fr/3-gestionmodule/module.asp
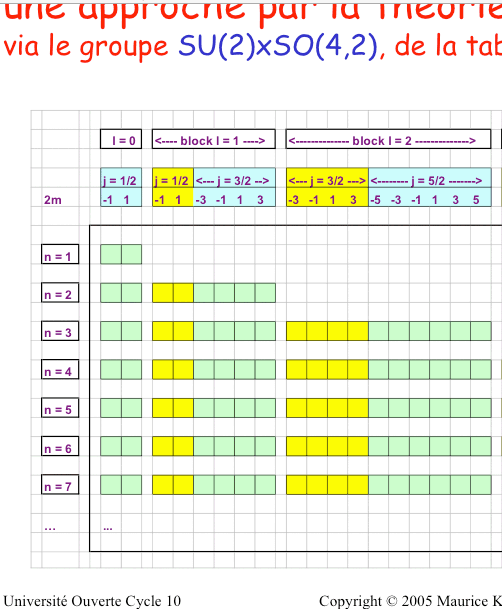

Fig.22bis, 19. Figure de Kibler explicative de son Tableau 1. Réf. Fig. 29, 67. Les rangées sont les couches n = 1, 2, 3,..., les colonnes sont les portions de sous-couches divisées selon les valeurs du paramètre j égal à lą(1/2), avec l = 0, 1, 2, 3. Avec permission demandée à l'auteur.
Couplages j ou couplages l et s
Je reviens sur l'observation précédente et je la développe concernant les sous-couches renfermant les éléments irréguliers chrome Cr24 et molybdène Mo42, qui se trouvent dans une sous-couche p avec l = 2 et n = 3 et 4 respectivement. Fig. 22ter.
Si Cr24 et Mo42 représentaient la saturation du fragment j = 3/2 de la sous-couche l = 2, on s'attendrait à ce qu'ils soient des éléments réguliers, au contraire de l'expérience. Ils sont irréguliers, ce que marque l'astérisque*. Cela suggère que la fragmentation selon j manque de signification physique. Fig. 22ter. Je montre les demi sous-couches 2- et 2+. Les éléments Mn25, Tc43 etc font partie de la colonne vertébrale. Fig. 14,43 et ailleurs. Fig. 22ter,9.
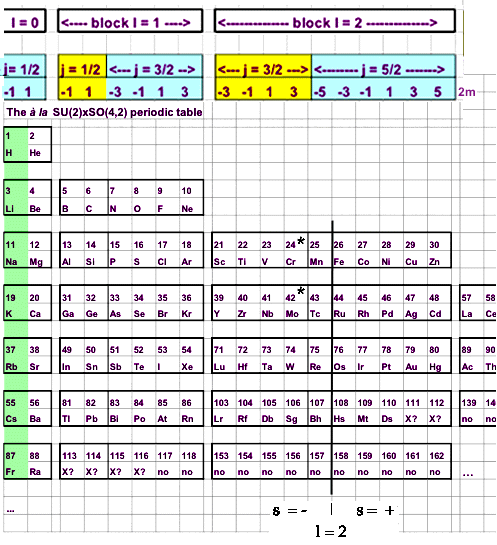
Fig. 22ter,9. D'après Kibler fig. 9 et passim. Si Cr24 et Mo42 représentaient la saturation du fragment j = 3/2 de la sous-couche l = 2, on s'attendrait à ce qu'ils soient des éléments réguliers, au contraire de l'expérience. Ils sont irréguliers, ce que marque l'astérisque*. Cela suggère que la fragmentation selon j manque de signification physique. Je montre les demi sous-couches 2- et 2+. Les éléments Mn25, Tc43 etc font partie de la colonne vertébrale Fig. 14,43 et ailleurs.
Maurice R. Kibler. Une question.
Maurice R. Kibler a fait paraître sur internet et ailleurs, depuis au moins 1983, une série remarquable d'études sur la classification des éléments, dont plusieurs développent et rationalisent le principe de construction Aufbau dans la théorie mathématique des groupes. Voici une liste de références qu'il m'a communiquée, ce dont je le remercie.
•
/LISTE \
web site:
•On the structure of matter from the Greeks to 2005 (in French)
http://spiral.univ-lyon1.fr/entree.asp?id=2770
recent papers:
•A group-theoretical approach to the periodic table of chemical elements: http://spiral.univ-lyon1.fr/entree.asp?id=2770
Old and new developments
http://xxx.lanl.gov/abs/quant-ph/0503039
•On a group-theoretical approach to the periodic table of chemical
elements
http://xxx.lanl.gov/abs/quant-ph/0408104
•On the use of the group SO(4,2) in atomic and molecular physics
http://xxx.lanl.gov/abs/quant-ph/0409209
•Classifying chemical elements and particles:
From the atomic to the sub-atomic world
http://xxx.lanl.gov/abs/quant-ph/0310155
•Fractional supersymmetric Quantum Mechanics as a set of
replicas of ordinary supersymmetric Quantum Mechanics
http://xxx.lanl.gov/abs/math-ph/0312019
•De la chimie à la physique subatomique :
des mots pour les constituants de la matière
http://democrite.in2p3.fr/democrite-00024034
textbook (second edition):
•Eléments de mathématiques pour la physique et la chimie
http://monsite.wanadoo.fr/math_physique_chimie/index.jhtml
\LISTE /
•
Question. Les symétries liées au spin de l'électron sont-elles correctement introduites dans les hypothèses à la base des calculs de Kibler? Je propose que ces symétries doivent être d'ordre quatre et qu'une représentation correcte réclame deux dimensions pour chaque rangée du tableau, trois pour l'ensemble.
/Correspondance 12 juin 2006\
> PierreDemers wrote:
> >
> > http://www.lisulf.quebec/gqajuin2.html
> >
> > Prof. Maurice Kibler,
> >
> > Cher collègue,
> >
> > Je souhaiterais avoir votre permission pour
> > utiliser une de vos figures du 18 mai 2005 dans
> > ce travail de moi : elle forme Fig 22bis.
> >
> > Est-ce que je vous cite correctement?
> >
> > Avec mes salutations amicales.
> >
> > Pierre Demers, prof. honoraire de l'Université de Montréal
Cher Professeur Demers,
Je vous autorise à utiliser la figure en question
à condition de bien mentionner sa source sous la
forme suivante :
On the structure of matter from the Greeks to 2005 (en français))
http://spiral.univ-lyon1.fr/entree.asp?id=2770
ainsi que les articles où cette figure est décrite :
A group-theoretical approach to the periodic table of chemical elements:
Old and new developments
http://xxx.lanl.gov/abs/quant-ph/0503039
On a group-theoretical approach to the periodic table of chemical
elements
http://xxx.lanl.gov/abs/quant-ph/0408104
Classifying chemical elements and particles:
>From the atomic to the sub-atomic world
http://xxx.lanl.gov/abs/quant-ph/0310155
De la chimie à la physique subatomique :
des mots pour les constituants de la matière
http://democrite.in2p3.fr/democrite-00024034
Avec mes respectueuses salutations.
Professeur M. Kibler
\Correspondance 12 juin 2006/
Éric Scerri sur la recherche de symétrie.
Éric Scerri, à propos des critères de symétrie, de beauté, élégance et vérité, a exprimé sa désapprobation de certains propos d'Einstein et de Dirac et sa défiance envers la recherche de symétrie dans le tableau des éléments. : "It may be completely misleadng to demand that the Periodic Table itself be symmetrical". Traduction : "Le Tableau Périodique lui-même doit-il être symétrique? Il me semble qu'une telle exigence soit trompeuse et ne mènerait à rien du tout". RK p, 149. Pourtant, la périodicité est une forme (modeste il est vrai) de symétrie que Scerri semble admettre dans le choix de ses mots ci-dessus, ce qu'il confirme au tableau p. 151.
L'opinion défavorable de Scerri envers une recherche de symétrie dans la classification atomique paraît bien risquée alors que telle recherche a été remarquablement fructueuse dans le domaine subatomique au siècle passé.
On peut établir un parallèle entre la recherche de symétrie dans le tableau des atomes et la recherche d'une structure en couches dans les noyaux, Il y a moins d'un siècle, certains physiciens réputés, dont Eugène Wigner et Édouard Teller, étaient d'avis que les noyaux n'obéissaient pas à un modèle en couche avec des nombres magiques jusqu'à ce que Maria Goeppert-Mayer, avec l'encouragement de Fermi, démontre le contraire et obtienne le Prix Nobel de physique en 1963. * Leçon à tirer : les idées reçues sont parfois erronées.*
Scerri aurait beau jeu critiquer mes contributions au chef d'une recherche incessante (et d'une réalisation) de symétrie et d'élégance dans le tableau périodique des éléments amélioré par moi depuis 1995. Il invoque le critère d'élégance pour approuver le tableau tridimensionnel de Dufour.
*Les nombreuses expériences et déceptions que les plus "anciens" ont accumulées au cours des ans les amènent souvent à adopter une approche trop conservatrice. Ce fut le cas de Wigner et d’autres grands physiciens du nucléaire qui avaient tenté en vain de développer un modèle en couches. Ils en étaient arrivés à penser que la spéculation sur les nombres magiques et les modèles en couches étaient une pure perte de temps. Même Teller se désintéressa de la question, se tournant vers d’autres domaines.
Mais Maria n’en démordit pas. Passionnément, elle continua à étudier les nombres magiques. Elle alla à l’encontre des physiciens de laboratoire, discutant dans les détails avec eux des données, et rassemblant tous les renseignements sur la stabilité et d’autres propriétés du noyau atomique qui pourraient suggérer une "structure d’oignon". Bientôt le célèbre physicien Wolfgang Pauli la surnomma la "madone de l’oignon".
http://www.prismeshebdo.com/prismes hebdo/article.php3?id_article=230
*In 1946 they went to Chicago. This was the first place where she was not considered a nuisance, but greeted with open arms. (Ils allèrent à Chicago en 1946. Ce fut le premier endroit où elle ne fut pas regardée comme une nuisance, mais au contraire accueillie à bras ouverts).
http://nobelprize.org /physics/laureates/1963/mayer-bio.html
Représentations tridimensionnelles.
Je rappelle en terminant la représentation en pyramide à base carrée de la figure13 et je mentionne la possibilité peu explorée d'une représentation en pyramide à base triangulaire, dessinant un tétraèdre régulier. Fig. 23.
Fig. 23, 10. Cent vingt cellules sphériques s'agencent en une pyramide tétraédrique. Deux étages forment une strate. Nombre quatre : un tétraèdre régulier a quatre faces.
Conclusions
Concluons cette analyse de l'intervention du nombre quatre dans le système du québécium : on reconnaîtra que le nombre quatre intervient abondamment dans le système du québécium appliqué à la mise en ordre rationnelle des éléments chimiques. De plus il offre au moins une amorce de solution aux deux problêmes encore irrésolus depuis de longues années des éléments irréguliers et de la coupure 4s/3d.
On reconnaîtra finalement que le nombre quatre intervient abondamment dans le système du québécium appliqué à la mise en ordre rationnelle des éléments chimiques.
Le monde est une tétralogie.
Les symétries d'ordre quatre que je présente ne sont pas l'effet d'un artifice. Elles ne sont pas l'effet du système du québécium avec son tableau elliptique. Le système du québécium avec son tableau elliptique ne fait que les révéler. Il est quasi-indispensable pour les révéler mais leur existence est indépendante de l'emploi du système du québécium. L'attachement exclusif au tableau traditionnel considéré comme une proposition pédagogique indiscutable retarderait la reconnaissance de cette vérité. Le système du québécium est particulièrement adapté à mettre en évidence la "tétralogie" des atomes et les conséquences qu'il faut en tirer.
"Le monde observable, étant formé par l'association des atomes, est fondamentalement une tétralogie".
J'essaierai, dans un travail qui suivra, d'interpréter les symétries de la classification par les symétries de l'atome qui sont associées aux cônes de précession des moments cinétiques propres et orbitaux.*
*Paul Verlaine (1844-1896), Prince des poètes en 1894.
"De la musique avant toute chose,
Et pour cela préfère l'Impair".
Art poétique, 1874
*L'impair trois dans l'alexandrin prête à sa mise en carré. Fig. 1, 0.

Fig. 1, 0 . Racine, Phèdre.
•
gqajuin2.html
Traduction interdite Tous droits de traduction réservés
Précédent gqajuin1.html Suivant à venir