HetJa.htm

Système du Québécium.

Géométrie et nombre magique 30. Édification d'un tableau symétrique 2D des éléments, de l'Hydrogène 1 au Janétium 120.

par Pierre Demers

1er décembre 2014.

Version du 22XII2014

Traduction interdite.

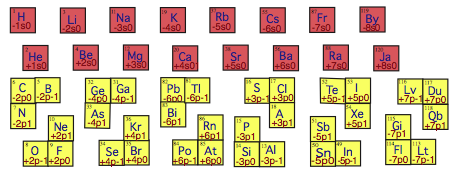
Effet Pauli, spin-, spin+. Effet Zeeman 1, 3, 5, 7.

..

Dans le tableau, l'ordre est ainsi: valeurs spin - de l'électron d'abord, puis spin +, ce qui établit une moitié Est et une moitié Ouest. C'est l'effet Pauli. Ensuite l'effet Zeeman, générateur d'équerres qui s'emboîtent

Le Tableau périodique des éléments bidimensionnel. Introduction.

Voici du CEGEP de Drummondville une introduction, avec réserves, à l'atome de Bohr.

"Structure électronique 41. Les valeurs des niveaux d’énergie calculées par Bohr correspondent parfaitement à celles du spectre d’émission de l’hydrogène. Cependant, le modèle de Bohr présente de sérieuses lacunes. Par exemple, quand on tente de l’appliquer à d’autres atomes que l’hydrogène, rien ne va plus. Le modèle de Bohr ne fonctionne que pour les espèces chimiques contenant un seul électron! Après diverses tentatives infructueuses pour tenterde l’améliorer, on a dû admettre qu’il n’y avait rien à faire: le modèle de Bohr était fondamentalement erroné."

Réf.1. www.cdrummond.qc.ca/cegep/scnature/chimie/NotesDeCours/ChimieNYA/chapitre2.pdf

Des auteurs ont dit que les atomes présentent une énigme discutée plus loin. Voici d'abord une introduction, où je reprends et mets à jour une argumentation parue en 2004. Réf. 2.

Voici un diagramme de l'atome H formé d'un proton et d'un électron.

. .

Fig. 2. L'atome d'hydrogène. Voilà 7 de ses états ou niveaux d'énergie, entièrement définis par le seul nombre quantique principal n. Pour n = 8, le niveau est -0,21 ev. Pour n quelconque, en ev, il est -13,6/n2.Les transitions entre 2 de ces niveaux sont à l'origine des rayonnements qu'il émet. Les niveaux individuels ont des correspondances avec l'organisation des 120 atomes du tableau des éléments. Le niveau le plus bas est -13,6 ev, le potentiel d'ionisation est 13,6 v. Il s'agit des énergies dues aux seules forces électromagnétiques entre le noyau et un électron. Au niveau 0 et plus haut, il y a ionisation avec apparition d'un proton et d'un électron libres. Réf. 3. Germain Salvato-Vallverdu

À retenir de cette figure: le niveau 1 est à la source de 2 éléments du tableau, soit l'hydrogène lui-même 1 H et l'hélium 2 He. Les autres niveaux, de 2 à 8, sont à la source des 118 autres éléments, de 3 Li à 120 Ja.

Théorie des atomes. Un atome est formé d'un noyau de charge positive valant un nombre entier z fois l'unité, et de z électrons. La théorie des atomes est calquée sur l'atome de Bohr modifié, qui concerne l'atome d'hydrogène, lequel est de nos jours bien compris. On lui associe les noms de Abraham, Balmer, Bloch, Dirac, Heisenberg, Pauli, Rutherford, Weyl et autres et l'équation de Schroedinger, qui s'applique admirablement au système formé d'un noyau positif associé par la force électromagnétique à un électron négatif. En revanche, cette dernière équation ne s'applique pas aux autres atomes, pluriélectroniques, avec z supérieur à 1. C'est alors un autre problème dit de trois corps, mieux vaudrait dire plus de 2 corps, car ce problème est connu en mécanique céleste, où il se prête à des méthodes de calcul satisfaisantes par approximations successives. Dans ces approximations, on ramène le problème à celui de 2 corps en considérant l'un des corps d'une part et la totalité des autres corps en présence, d'autre part.

Les 4 variables de la théorie des quanta

Spin, n, 1, m

spin qui vaut -1/2 ou + 1/2, en abrégé - ou +

n nombre quantique principal vaut un entier positif, 1, 2 ....

l nombre quantique azimutal vaut un entier positif plus petit que n.

Synonymie: 0, s, R; 1, p, J; d,2, V; f, 3, B; g, 4, Violet,

m nombre quantique magnétique, vaut un entier entre -l et l, 0 admis.

Tout atome, neutre ou ionisé, répond à une description par des nombres quantiques. Un atome pluriélectronique privé, par ionisation, de tous ses électrons sauf 1, est appelé un hydrogénoïde, et répond correctement à la théorie de Schroedinger avec un noyau de charge z au lieu de l'unité. Si ce qu'on appelle l'atome de Bohr s'appliquait à tous les éléments, leurs potentiels de 1re ionisation seraient tous égaux à 13,6 ev, comme pour l'hydrogène. Or l'expérience donne des résultats différents. Fig. 3.

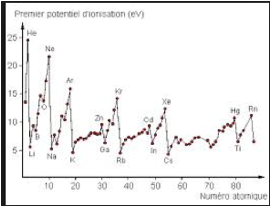
Fig. 3. Potentiels de 1re ionisation de quelques atomes. http://dc594.4shared.com/doc/gIusb5YS_26isRedirect_3Dtrue/preview.html

Il n'existe pas de théorie exacte des atomes autres que l'hydrogène. À partir de 2 He, dans un atome z > 2, il existe un potentiel de 2e ionisation.

Édification des atomes pluriélectroniques.

J'imagine ajouter un proton et un électron à la fois au noyau de l'hydrogène, avec un certain nombre de neutrons, totalisant z protons et z électrons. J'imagine que chaque paire proton-électron vient de l'un des états d'un atome d'hydrogène qui est utilisé en conservant les valeurs n et l qui lui appartiennent, ces niveaux pouvant être utiisés plus d'une fois.

On a trouvé que les apports successifs se font à partir d'une liste définie qui est celle des niveaux ou états n = 1 à 8 de l'atome 1H, augmentée et modifiée par deux effets. À cette liste, je lui donne l'appellation H source. Je me répète: pour les fins de cette édification, le niveau déplacé est défini par deux nombres quantiques: n et l, qui se conservent dans le résultat de l'atome une fois édifié.

Effet Pauli, le spin de l'électron, qui peut être - ou +. Il double le nombre d'états autrement disponibles, - est le plus bas par convention.

Effet Zeeman. Cet effet ajoute le nombre quantique magnétique m. Ce nombre magnétique multiplie par 1, 3, 5 ou 7 le nombre d'états disponibles, selon qu'il s'agit d'un état s, p, d ou f, respectivement. Dans le langage couleurs du système du Québécium. RJVB correspond aux nombres quantiques l = 1, 2, 3, 4 ou spdf. Les valeurs - de m d'abord. Fig. 1.

Pour un atome z, je distingue son caractère et sa formule.

Pour le 120 Ja janétium, le nméro atomique est 120, le caractère est.

Caractère du 120 Ja est

8s0

Sa formule comprend en outre 119 termes écrits à gauche de son caractère. La voici, je la suppose écrite sur une seule ligne, repliée à cause de sa longueur.

(NB1: spin, n, l, m)

(NB2: | séparateur)

Formule du 120 Ja est

-1s0 1s0 -2s0 +2s0 | -2p-1 -2p0 -2p1 +2p-1 +2p0 +2p1 -3s0 +3s0 | -3p-1 -3p0 -3p1 +3p-1 +3p1 -3p-1 0 -

etc. Voyez Tableau 3 dans Réf. 1.

Formule du 120 Janétium

La formule du janetium 120 ci-dessus contient celle de chacun des autres atomes qui le précèdent, de 1 H à 119 By. La formule d'un atome z contient son caractère propre augmenté des caractères de tous les atomes précédents depuis l'hydrogène: c'est sa formule.

Par exemple la formule du 5 Bore, dans l'ordre. S'il n'y a pas le signe -, le signe + est sous-entendu.

-1s0 1s0 -2s0 2s0 -2p-1

Le caractère du 5 Bore est le dernier terme à droite.

-2p-1

qui détermine la case de son placement dans le tableau des éléments. Les électrons libres sont tous semblables, mais dans un atome, il n'y a pas 2 électrons ayant les 4 mêmes valeurs spin, n, l, m. On doit parler d'une entité globale noyau et électrons, où on peut discerner des paires noyau - électron, ayant un caractère défini. La collection de ces paires est la formule de l'atome. En écriture symbolique, voici la formule nominale de l'atome z, avec une suggestion de la source

Formule nominale de l'atome z = Somme (de 1 à z) (niveaux H X Pauli X Zeeman)

Il faut ajouter la formule réelle, dont on sait qu'elle diffère de la formule nominale dans 19 atomes dits irréguliers. Pour ces atomes irréguliers.

Formule réelle de l'atome z = Somme (1 à zt avec lacunes, voir Tableau 2 Fig. 6) niveaux H X Pauli X Zeeman

Pour les 101 autres atomes.

Formule réelle = Formule nominale

Correspondances.

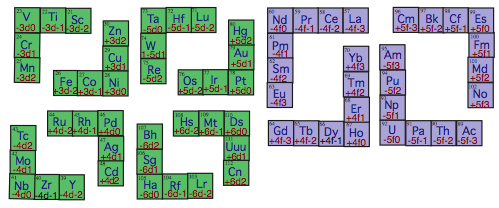
Voici le tableau des 120 atomes avec leurs caractères. Tableaux 1, 2

Pour un atome d'hydrogène, voici la liste des triplets de valeurs de n et l permises, avec le nombre de valeurs de m permises par l'effet Zeeman, selon la règle m = un entier entre -l et l, 0 admis.

1, 0, 1

total nombre de valeurs 1

2, 0, 1

2, 1, 3

total nombre de valeurs 4

3, 0, 1

3, 1, 3

3, 2, 5

total nombre de valeurs 9

4, 0, 1

4, 1, 3

4, 2, 5

4, 3, 7

total nombre de valeurs 16

Grand total jusqu'ici: 30.

Puis...

5, 0, 1

5, 1, 3

5, 2, 5

5, 3, 7

5, 4, 9

total nombre de valeurs 25

Pour chacune de ces paires, voici les valeurs de m permises écrites sous la forme de triplets et le nombre de ces triplets

1, 0: 0, 1 valeur de m

2, 0: 0, 1 valeur de m

2, 1: -1, 0, 1

2, 1: -1, 0, 1

Tableau 1.

Système du Québécium.

Formule du 120 Ja Janétium. 120 termes

Niveaux de H, n, l, à partir du plus bas, -13,6 ev. Spin - d'abord, avec toutes valeurs m Zeeman. Puis spin + avec toutes valeurs de m Zeeman.

L'ordre des atomes est imposé par l'expérience. On peut morceler la liste tel que dans la colonne de gauche, où ils sont groupés en 4 strates de 2 périodes chacune, selon le plan décrit plus bas. À droite, le morcellement en 7 périodes selon le tableau traditionnel de Mendeleev.

La colonne centrale énumère les états de l'atome H

qu'on peut associer à l'

élément. La somme des entrées .................................Atome H source ..............................Selon les 7 périodes

est la formule nominale du 120 Janétium

suite des niveaux correspondant aux états d'atomes H

modifiés par effet Pauli et effet Zeeman.........................États en ev croissant vers le bas.

z nominal..Nom.......Caractère nominal...................n quantum principal, l quantum azimutal

.........................................spin, n, l, m.

Un élément renferme l'entrée sur sa propre ligne,

augmentée des entrées sur les lignes précédentes

depuis z = 1.

Numéro z Période Mendeleev.

Strate 1. Période 1

1 H Hydrogène -1s0 1 0 -13,6 1

2 He Hélium +ls0 1 0 -13,6 1

Période 2

3 Li Lithium -2s0 2 0 -3,4 2

4 Be Béryllium +2s0 2 0 -3,4 2

Strate 2.

5 B Bore -2p-l 2 1 -3,4 2

6 C Carbone -2p0 2 1 -3,4 2

7 N Azote -2pl 2 1 -3,4 2

8 O Oxygène +2p-l 2 1 -3,4 2

9 F Fluor +2p0 2 1 -3,4 2

10 Ne Néon +2pl 2 1 -3,4 2

Période 3

11 Na Sodium -3s0 3 0 -1,51 3

12 Mg Magnésium +3s0 3 0 -1,51 3

13 Al Aluminium -3p-l 3 1 -1,51 3

14 Si Silicium -3p0 3 1 -1,51 3

15 P Phosphore -3pl 3 1 -1,51 3

16 S Soufre +3p-l 3 1 -1,51 3

17 Cl Chlore +3p0 3 1 -1,51 3

18 A Argon +3pl 3 1 -1,51 3

Période 4.

19 K Potassium -4s0 4 0 -0,85 4

20 Ca Calcium +4s0 4 0 -0,85 4

Strate 3.

21 Se Scandium -3d-2 3 2 -1,51 4

22 Ti Titane -3d-l 3 2 -1,51 4

23 V Vanadium -3d0 3 2 -1,51 4

24 Cr* Chrome -3dl 3 2 -1,51 4

25 Mn Manganèse -3d2 3 2 -1,51 4

26 Fe Fer +3d-2 3 2 -1,51 4

27 Co Cobalt +3d-l 3 2 -1,51 4

28 Ni Nickel +3d0 3 2 -1,51 4

29 Cu* Cuivre +3dl 3 2 -1,51 4

30 Zn Zinc +3d2 3 2 -1,51 4

31 Ga Gallium -4p-l 3 2 -1,51 4

32 Ge Germanium -4p0 3 2 -1,51 4

33 As Arsenic -4pl 3 2 -1,51 4

34 Se Sélénium +4p-l 3 2 -1,51 4

35 Br Brome +4p0 3 2 -1,51 4

36 Kr Krypton +4p1 3 2 -1,51 4

Période 5.

37 Rb Rubidium -5s0 5 0 -0,54 5

38 Sr Strontium +5s0 5 0 -0,54 5

39 Y Yttrium -4d-2 4 2 -0,85 5

40 Zr Zirconium -4d-l 4 2 -0,85 5

41 Nb* Niobium -4d0 4 2 -0,85 5

42 Mo* Molybdène -4dl 4 2 -0,85 5

43 Te Technétium -4d2 4 2 -0,85 5

44 Ru* Ruthénium +4d-2 4 2 -0,85 5

45 Rh* Rhodium +4d-l 4 2 -0,85 5

46 Pd * Palladium +4d0 4 2 -0,85 5

47 Ag * Argent +4dl 4 2 -0,85 5

48 Cd Cadmium +4d2 4 2 -0,85 5

49 In Indium -5p-l 5 1 -0,54 5

50 Sn Étain -5p0 5 1 -0,54 5

51 Sb Antimoine -5pl 5 1 -0,54 5

52 Te Tellure +5p-l 5 1 -0,54 5

53 I Iode +5p0 5 1 -0,54 5

54 Xe Xénon +5pl 5 1 -0,54 5

Période 6.

55 Cs Césium -6s0 6 0 -0,38 6

56 Ba Baryum +6s0 6 0 -0,38 6

Strate 4.

57 La* Lanthane -4f-3 4 3 -0,85 6

58 Ce * Cérium -4f-2 4 3 -0,85 6

59 Pr Praséodyme -4f-l 4 3 -0,85 6

60 Nd Néodyme -4f0 4 3 -0,85 6

61 Pm Prométhéum -4fl 4 3 -0,85 6

62 Sm Samarium -4f2 4 3 -0,85 6

63 Eu Europium -4f3 4 3 -0,85 6

64 Gd* Gadolinium +4f-3 4 3 -0,85 6

65 Tb Terbium +4f-2 4 3 -0,85 6

66 Dy Dysprosium +4f-l 4 3 -0,85 6

67 Ho Holmium +4f0 4 3 -0,85 6

68 Er Erbium +4fl 4 3 -0,85 6

69 Tm Thulium +4f2 4 3 -0,85 6

70 Yb Ytterbium +4f3 4 3 -0,85 6

71 Lu Lutécium -5d-2 5 2 -0,54 6

72 Hf Hafnium -5d-l 5 2 -0,54 6

73 Ta Tantale -5d0 5 2 -0,54 6

74 W Tungstène -5dl 5 2 -0,54 6

75 Re Rhénium -5d2 5 2 -0,54 6

76 Os Osmium +5d-2 5 2 -0,54 6

77 Ir Iridium +5d-l 5 2 -0,54 6

78 Pt* Platine +5d0 5 2 -0,54 6

79 Au* Or +5dl 5 2 -0,54 6

80 Hg Mercure +5d2 5 2 -0,54 6

81 TI Thallium -6p-l 6 1 -0,37 6

82 Pb Plomb -6p0 6 1 -0,37 6

83 Bi Bismuth -6pl 6 1 -0,37 6

84 Po Polonium +6p-l 6 1 -0,37 6

85 At Astatine +6p0 6 1 -0,37 6

86 Rn Radon +6pl 6 1 -0,37 6

Période 7.

87 Fr Francium -7s0 7 0 -0,28 7

88 Ra Radium +7s0 7 0 -0,28 7

89 Ac* Actinium -5f-3 5 3 -0,54 7

90 Th* Thorium -5f-2 5 3 -0,54 7

91 Pa* Protoactinium-5f-l 5 3 -0,54 7

92 U* Uranium -5f0 5 3 -0,54 7

93 Np* Neptunium -5f 5 3 -0,54 7

94 Pu Plutonium -5f2 5 3 -0,54 7

95 Am Américium -5f3 5 3 -0,54 7

96 Cm* Curium +5f-3 5 3 -0,54 7

97 Bk Berkélium +5f-2 5 3 -0,54 7

98 Cf Californium +5f-l 5 3 -0,54 7

99 Es Einsteinium +5f0 5 3 -0,54 7

100 Fm Fermium +5fl 5 3 -0,54 7

101 Md Mendélévium+5f2 5 3 -0,54 7

102 No Nobélium +5f3 5 3 -0,54 7

103 Lr Lawrencium -6d-2 6 2 -0,37 7p

104 Rf Rutherfordium-6d-l 6 2 -0,37 7

105 Ha Hahnium -6d0 6 2 -0,37 7

106 Sg Seaborgium -6dl 6 2 -0,37 7

107 Bh Bohrium -6d2 6 2 -0,37 7

108 Hs Hassium +6d-2 6 2 -0,37 7

109 Mt Meitnerium +6d-l 6 2 -0,37 7

110 Ds Darmstadtium+6d0 6 2 -0,37 7

111 Uuu** Unununium +6dl 6 2 -0,37 7

112 Uub** Copernicium +6d2 6 2 -0,37 7

113 Lt Lortium -7p-1 6 1 -0,28 7

114 Uuq** Flérovium -7p0 6 1 -0,28 7

115 Gi Giguérium -7p1 6 1 -0,28 7

116 Uuh** Livermorium +7p-l 6 1 -0,28 7

117 Du Dufourium +7p0 6 0 -0,28 7

118 Qb Québécium +7pl 6 0 -0,28 7

(Période 8, inexistante

dans le tableau de Mendeleev.

119 By Barthélémyum-8s0 6 0 -0,21 (8

120 Ja Janetium +8s0 6 0 -0,21 (8

** Appellation temporaire de l'UIPPA.

Synonymie.

120 Ubn, 119 Uue, 118 Uuo, 117 Uus, 115 Uup, 113 Uut.

* signifie élément irrégulier.

Tableau 2

Les 19 éléments irréguliers*.

zt électron terminal réel. On donne z, zt et les lacunes et la formule depuis le gaz rare précédent.

Le symbole en fin de ligne est celui qui a, ou aurait s'il était régulier, ce numéro atomique, exemples 30Zn, 45Rh.

Cr* 24,25, (non 20) 18A 19 21 22 23 24 25Mn

Cu* 29,30, (non 20) 18A 19 21 22 23 24 25 26 27 28 29 30Zn

Nb* 41,42, (non 38) 36 Kr 37 39 40 41 42Mo

Mo* 42,43, (non 38) 36 Kr 37 39 40 41 42 43Tc

Ru* 44,45, (non 38) 36Kr 37 39 40 41 42 43 44 45Rh

Rh* 45,46, (non 38).. 36Kr 37 39 40 41 42 43 44 45 46Pd

Pd* 46,48, (non 37,38) ).. 36Kr 39 40 41 42 43 44 45 46 47 48Cd

Ag* 47,48, (non 38) ).. 36Kr 37 39 40 41 42 43 44 45 46 47 48Cd

La* 57,71, (non 57 à 70).. 54Xe 55 56 71Lu

Ce* 58,71, (non 58 à 70) ).. 54Xe 55 56 57 71Lu

Gd* 64,71, (non 64 à 70).. 54Xe 55 56 57 58 59 60 61 62 63 71Lu

Pt* 78,79, (non 56).. 54Xe 55 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79Au

Au* 79,80, (non 56).. 54Xe 55 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80Hg

Ac* 89,103, (non 89 à 102).. 86Rn 87 88 103Lr

Th* 90,104, (non 89 à 103).. 86Rn 87 88 104Rf

Pa* 91,103, (non 91 à 102) 86Rn 87 88 89 90 103Lr

U* 92,103, (non 92 à 102).. 86Rn 87 88 89 90 91 103Lr

Np* 93,103, (non 93 à 102).. 86Rn 87 88 89 90 91 92 103Lr

Cm* 96 103, (non 96 à 102) .. 86Rn 87 88 89 90 91 92 93 94 95 103Lr

Formule du 120 Janetium. Un plan d'organisation.

Disposant donc de la liste des atomes z = 1 à 120, je crée un plan pour organiser davantage leur présentation, dans l'ordre. Ce sera un tableau, de la catégorie des graphismes bidimensionnels.

Règle 1. Je me donne un carrelage indéfini de carrés vides.

Ce graphisme, je le place dans les cases d'un carrelage indéfini, dont je tire un carrelage distinct pour chaque strate à faire apparaître. (Anticipant sur ce qui suit: il s'agit de remplir successivement des carrelages carrés ayant comme côté 2, 4, 6 et 8 cases, et je me donne des règles pour occuper les cases.) Voici le plus grand carrelage, lequel contient tous les autres. Il a 8 cases de côté. Je lui associe une rose des vents.Fig. 6.

Ouest - spin + Est

N

..

S

Fig. 6. Carrelage carré ayant 8 cases de côté. Ouest O à gauche, Est E à droite. QbS2Fig297.3.gif

Règle 2. Affectation des cases. Par moitiés, Ouest spin -, Est spin +.

Règle 3. Case de début de strate. La 1re case occupée sera dans le quadrant NO, au plus près du centre de figure. Ainsi se trouve désigné un carré, centré sur l'origine.

Je chemine à partir du niveau le plus profond de H, -13,6 ev, n=1, l=0, doublé à cause de Pauli, spin - d'abord. Puis spin + et c'est He n = 2.

Règle 4. Case suivante. Les cases que je choisis d'occuper sont au plus près du centre de figure en regard càd, en symétrie par rapport au centre du carrelage, en diagonale NO, SE. Voici un placement réalisé. Il reste dans le carré 2 cases vides. Fig. 6

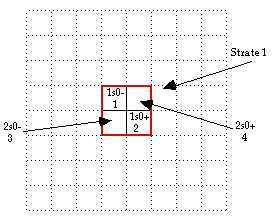
Fig. 6. Placement de H et de He. QbS2Fig298

Règle 5. Le carré désigné doit être rempli avant d'aborder un nouveau carré.

La suite: placement de Li et Be, les cases sont toutes occupées. Fig. 7.

.

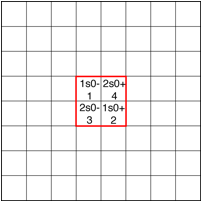
Fig. 7. Placement de Li et de Be. Strate 1.png

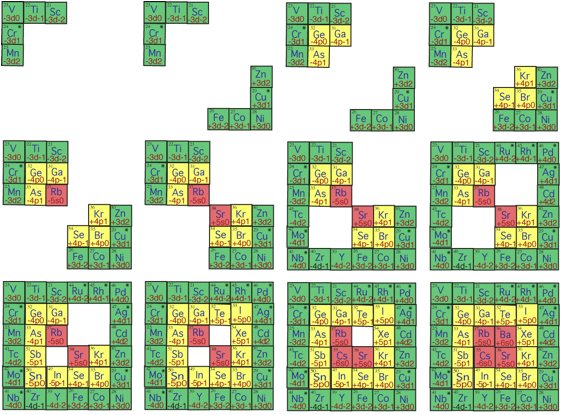
Et la strate 1 est complétée. Il me faut passer à réaliser la strate 2. Dans ce qui suit, je me dispenserai de récrire le canevas de carrés, son rôle est suffisamment suggéré par l'arrangement en équerres que voici.

Régle 6. Créer des équerres Zeeman. Une 1re strate étant remplie, je crée une nouvelle strate, soit ici, une strate 2, que j'amorce dans le quadrant NO, avec les éléments B, C et N qui sont tous -2p, formant un groupe Zeeman. Je choisis de former chacun des groupes Zeeman en une équerre.

Je dis que tous les éléments font partie d'un groupe Zeeman, même les éléments s ayant m = 0 que je considère comme des équerres sans bras. Les autres éléments font partie d'équerres ayant des bras de 1, 2 ou 3 cases, et pointent obligatoirement selon une diagonale de la rose des vents.

Voici une collection des équerres, chacune sous la forme de cubes pour la manipulation, aux nombres de 1, 3, 5 ou 7 cubes. Cette collection contient tous les éléments de z = 1 à 120. Pour une présentation graphique, je recours à des cases carrées. Figs 8, 9.

NDLR. Dans les figures 8 et 9, les graphismes de droite sont des mises à jour des photos de gauche.

. ..

Fig. 8. Les 16 équerres s sans bras. Je les nomme par le seul élément qu'elles contiennent: 1 H, 2 He, 3 Li, 4 Be, 11 Na, 12 Mg, 19 K, 20 Ca, 37 Rb, 38 Sr, 55 Cs, 56 Ba, 87 Fr, 88 Ra, 119 By, 120 Ja.

Les 12 équerres ayant ayant 2 bras d'une case. Je les nomme par le 1er des éléments qu'elles contiennent, dans l'ordre: 5 B, 8 O, 13 Al, 16 S, 31 Ga, 34 Se, 49 In, 52 Te, 81 Tl, 84 Po, 113 Uut ou Lt, 116 Lv, Parmi ces équerres, 3 sont orientées NO, 3 orientées SE, 3 orientées SO et 3 orientées NE.

image017.pct, HHeLtFl.ai

. ..

Fig. 9. Les 8 équerres d ayant 2 bras de 2 cases. Je les désigne par le 1er des éléments qu'elles contiennent: 21 Sc, 26 Fe, 39 Y, 44 Ru, 71 Lu, 76 Os, 103 Lr, 108 Hs.

Parmi ces équerres, 2 sont orientées NO, 2 orientées SE, 2 orientées NE et 2 orientées SE.

Les 4 équerres f ayant 2 bras de 3 cases. Je les désigne par le 1er des éléments qu'elles contiennent: 57 La, 64 Gd, 89 Ac, 96 Cm

Parmi ces équerres, une est orientée NO, une orientée NE, une orientée SO et une orientée SE,

image019.png, VTiThAc.ai,

Règle 7. Sens de rotation. Il me faut choisir un sens de rotation dans les équerres ayant des bras non nuls. Je crée la 1re équerre ainsi rencontrée BCN dans le sens de rotation anti-horloge. Cela est déterminant pour la création des autres équerres présentées Figs 8, 9 et l'occupation des cases des carrés des strates 2, 3 et 4

Sens de rotation. Rotation anti-horloge dans les quadrants NO e SE, rotation horloge dans les quadrants SO et NE. La règle s'énonce ainsi:

Rotations dans les quadrants: NO et SE: rotation anti-horloge; SO et NE: rotation horloge. Les flèches incurvées Fig. 10.

..

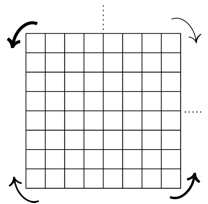
Fig. 10. L'écriture est anti-horloge aux quadrants NO et SE, horloge aux quadrants SO et NE. flèches.png

L'ordre du remplissage des quadrants est selon l'épaisseur des traits des flèches.

Muni de ces équerres, je m'affaire à meubler les strates 1, 2, 3, 4. Ici je remarque que la 1re équerre B, C, N rencontrée, placée au plus près du centre de figure dans le quadrant NO, désigne un carré ayant 4 cases de côté. Je place immédiatement en regard la 2e équerre 8 O. Fig. 11.

Voici les étapes du remplissage de la strate 1 par les 4 équerres sans bras. Fig. 11.

. .Source H utilisée, valeurs n et l: 1 0, 2 0.

Fig. 11. En 4 étapes, le remplissage de la strate 1 en 4 étapes par les 4 équerres sans bras de 1 H à 4 Be. Lesstrates1et221h157XII2014, 2.Publication

Voici les 8 étapes du remplissage de la strate 2 par 8 équerres. Fig. 12.

.. Source H utilisée, valeurs n et l: 2 1, 3 0; 3 1, 4 0.

Fig. 12. En 8 étapes, le remplissage de la strate 2 en 8 étapes par 8 équerres de 5 B à 20 Ca. Les strates1et221h157XII2014.

Voici les étapes du remplissage de la strate 3 par 12 équerres. Fig. 13.

. . Source H utilisée, valeurs n et l: 3 2, 4 1, 5 0; 4 2, 5 1, 6 0.

Fig. 13. Les 12 étapes du remplissage de la 3e strate, de 21 Sc à 56 Sr, par 12 équerres s, p et d. ScàBa9hyclesirréguliers5010XII2014, 2.Publication

. .

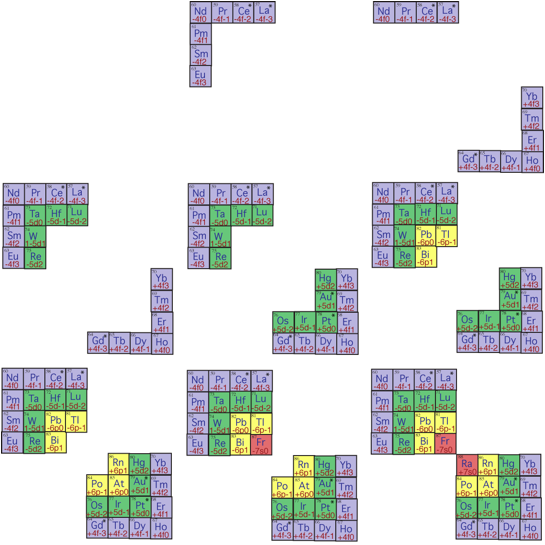Fig. 14. Strate 4. Les 8 premières étapes sur 16 du remplissage de la strate 4, de 57 La à 88 Ra, par les équerres s, p, d et f. LaàRaycirréguliers18h4710XII2014.png, 2.Publication

. Source H utilisée, valeurs n et l: 4 3, 5 2, 6 1, 7 0; 5 3, 6 2, 7 1, 8 0.

Fig. 15. Strate 4. Suite et fin du remplissage de la strate 4, les 8 dernières étapes. 89 Ac à 120 Ja. AcàJaycirréguliers18h2010XII2014.png, 2.Publication

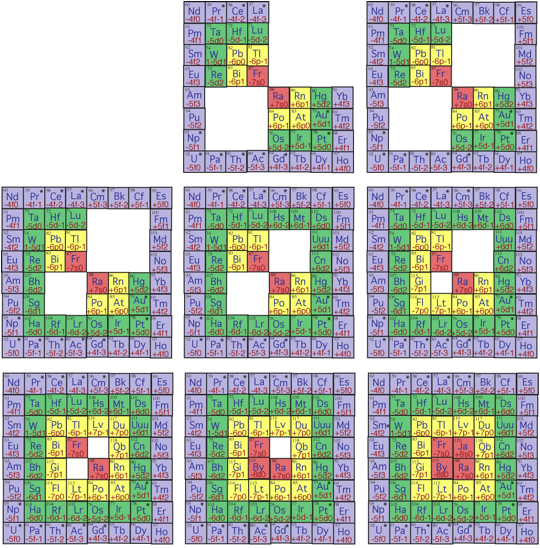
Et voici la totalité ses remplissages accomplis, sous la forme d'un tableau des éléments en demi-ellipse. Fig. 16.

. .

Fig. 16. D'après ci-dessus, tableau des éléments en demi-ellipse. H à Ja y compris irréguliers11XII2014.png, 2.Publication

Ainsi se trouve obtenu, par 7 règles géométriques, le tableau en demi - ellipse, qui manifeste une symétrie 4 et répond au nombre magique 30.

Une énigme du tableau périodique. Quelle énigme?

L'énigme du tableau périodique selon Scerri, appuyant ou reprenant des considérations semblables émises par d'autres auteurs.

Voici ce que je trouve dans une publication d'Eric Scerri. Réf. 2.

(Trad. et soulignés de rédaction)) "Les règles gouvernant l’attribution des nombres quantiques furent rigoureusement expliquées par la théorie quantique, de sorte que les 2 1res couches contiennent au maximum 2 et 8 électrons – et on eut ainsi enfin une explication des longueurs des 2 1res périodes du tableau !

Des considérations semblables appliquées aux couches 3 et 4 annoncent 18 et 32 électrons respectivement, mais cela ne s’accorde pas avec la répartition des éléments dans le tableau périodique. Et c’est là tout un problème : la 3e période contient 8 électrons au lieu de 18."

Je commence par la couche 3. Si je comprends bien cet auteur, il se réfère à un tableau dont la 3e période contient 8 éléments alors qu'elle devrait en contenir 18.

Couche 3.

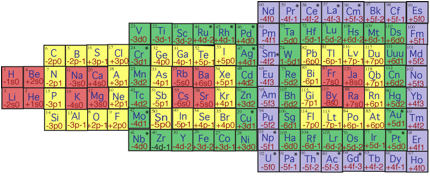
Pourquoi le 3e période devrait-elle contenir 18 éléments? Cette hypothèse peut se comprendre si on se réfère à un tableau de Mendeleev traditionnel, par exemple celui du CNRS illustré Fig. 17 et si on extrapole à partir du contenu des périodes 1 et 2, qui se terminent sur un gaz rare: 2 He puis 10 Ne, voyez la colonne Mendeleev du Tableau 1. Un alcalin commence la période 2.

Ces périodes 1 et 2 renferment toutes les possibilités offertes par Zeeman pour n = 1 et n = 2 respectivement, soit 2 et 2+6 = 8 éléments. Pour n = 3 ces possibilités sont 2+8+10 = 18, alors que ce qui est réalisé, c'est 2+8 = 10 seulement. En extrapolant sur cette base, les éléments Sc à Zn, dérivant de H n = 3, devraient intervenir, avec des numéros z de 19 à 28, suivis de K qui serait 29 K et de Ca qui serait 30 Ca. Or l'ordre est inversé, 29 K et 30 Ca se présentent avant la suite 31 Sc 40 Zn.

..

Fig. 17. Un tableau de Mendeleev du CNRS. au format pdf .

Ceci est, dans son début, la ligne 3 de Fig. 17.

11Na 12Mg 13Sc 14Ti 15V 16Cr 17Mn 18Fe 19Co 20Ni 21Cu 22Zn 23Al 24Si 25P 26S 27Cl 28Ar

Fig. 18. La ligne 3 de Fig. 17 remaniée, le 3e terme étant tiré se la ligne suivante 4.

Dès lors, la ligne 4 commencerait avec 29K, au lieu de 19, puis 30Ca au lieu de 20....

Couche 4.

Je pourrais faire une présentation analogue pour la période suivante qui serait la 4e.

Une solution à l'énigme?

Il me semble que le fondement de l'extrapolation de Scerri est bref quoique réel: les périodes 1 et 2 du tableau de Mendeleev. Tant qu'on récrira ce tableau de la même façon, ce fondement continuera de se présenter, on aura beau dire qu'un tableau n'est qu'un tableau. Il perpétue l'inquiétude d'une énigme.

En revanche, le processus d'édification du tableau par géométrie que je propose ici-même ne fait pas apparaître de discontinuïté particulière au voisinage du scandium.

Je suggère qu'une solution de l'énigme décrite se trouve dans l'adoption du tableau par géométrie que je propose. Il n'est pas exclu qu'il existerait des solutions équivalentes.

Remerciements.

Je remercie Patrick Callet et Maurice Kibler, qui ont présenté à Montréal récemment des communictions concernant le Système du Québécium. Leurs observations m'ont déterminé à rédiger le présent texte. Réfs 3, 4.

À suivre...

22XII2014

Références.

Réf. 1. Voyez le texte paru en 2004 dans le disque CD accompagnant le livre papier Pierre Demers 2004, Système du Québécium, La nouvelle classification des éléments, PUM 2004. ISBN 2-9802454-7-X. Il est présent en libre accès sur la toile: H et Qb : un parallèle entre les états. Fichier 23bis http://www.er.uqam.canobel/c3410/Fichier23bis.html

Voir aussi le texte papier de ce livre papier, accessible en libre accès sur la toile.

H et Qb : un parallèle entre les états par Pierre Demers

Le présent texte en est une mise à jour en 2014. En voici un extrait, modifié afin que le dernier terme soit 8s0+ Janétium 120, et non 7p1+ Québécum

Tableau 3. Formule du janétium.

Numéros électroniques 1 à 120

Numéros

1 à 10	1s0-	1s0+	2s0-	2s0+	2p-1-	2p0-	2p1-	2p-1+	2p0+	2p1+
11 à 20	3s0-	3s0+	3p-1-	3p0-	3p1-	3p-1+	3p0+	3p1+	4s0-	4s0+
21 à 30	3d-2-	3d-1-	3d0-	3d1-	3d2-	3d-2+	3d-1+	3d0+	3d1+	3d2+
31 à 40	4p-1-	4p0-	4p1-	4p-1+	4p0+	4p1+	5s0-	5s0+	4d-2-	4d-1-
41 à 50	4d0-	4d1-	4d2-	4d-2+	4d-1+	4d0+	4d1+	4d2+	5p-1-	5p0-
51 à 60	5p1-	5p-1+	5p0+	5p1+	6s0-	6s0+	4f-3-	4f-2-	4f-1-	4f0-
61 à 70	4f1-	4f2-	4f3-	4f-3+	4f-2+	4f-1+	4f0+	4f1+	4f2+	4f3+
71 à 80	5d-2-	5d-1-	5d0-	5d1-	5d2-	5d-2+	5d-1+	5d0+	5d1+	5d2+
81 à 90	6p-1-	6p0-	6p1-	6p-1+	6p0+	6p1+	7s0-	7s0+	5f-3-	5f-2-
91 à 100	5f-1-	5f0-	5f1-	5f2-	5f3-	5f-3+	5f-2+	5f-1+	5f0+	5f1+
101 à 110	5f2+	5f3+	6d-2-	6d-1-	6d0-	6d1-	6d2-	6d-2+	6d-1+	6d0+
111 à 120	6d1+	6d2+	7p-1-	7p0-	7p1-	7p-1+	7p0+	7p1+	8s0-	8s0+

Réf. 2. Éric Scerri 2007, (L’héritage Mendéléévien : le système périodique) Mendeleev’s Legacy: The Periodic System, ©2007 , No 1, http://www.chemheritage.org/pubs//ch-v25n1-articles/feature_mendeleev_print.html

(Cette adresse m'est restée inaccessible en 2014.)

A. "Les règles gouvernant l’attribution des nombres quantiques furent rigoureusement expliquées par la théorie quantique, de sorte que les 2 1res couches contiennent au maximum 2 et 8 électrons – et on eut ainsi enfin une explication des longueurs des 2 1res périodes du tableau !

Des considérations semblables appliquées aux couches 3 et 4 annoncent 18 et 32 électrons respectivement, mais cela ne s’accorde pas avec la répartition des éléments dans le tableau périodique. Et c’est là tout un problème : la 3e période contient 8 électrons au lieu de 18."

Et la 4e, ... 32?

"Tout compte fait, les nombres quantiques paraissent fournir une explication déductive satisfaisante du nombre total que chaque couche peut renfermer, mais en revanche la correspondance de ces valeurs avec les nombres d’éléments dans les périodes est en quelque sorte une coïncidence fortuite. L’ordonnance bien connue du remplissage des orbitales spdf* (*diagramme manquant) a été déterminée essentiellement de façon empirique. Bohr a échoué à déduire l’ordre du remplissage des orbitales, et comme certains auteurs l’ont reconnu, c’est là un des grands problèmes de la mécanique quantique.…Concernant le système de Mendeleev, la question n’est plus de savoir s’il est valide, mais plutôt, de trouver quelle serait la meilleure manière de le représenter**……"

The rules that govern the assignment of quantum numbers are rigorously explained by quantum theory, with the outcome that the first 2 shells contain a maximum of 2 and 8 electrons—at long last an explanation for the lengths of the first two periods of the table! Similar considerations for the 3rd and 4th shells predict 18 and 32 electrons respectively, but this is not in accordance with the arrangement of the elements in the periodic table.The problem is this: the third row of the periodic table contains 8, not 18, electrons.

It turns out that while quantum numbers provide a satisfying deductive explanation of the total number of electrons that any shell can hold, the correspondence of these values with the number of elements that occur in any particular period is something of a coincidence. The familiar sequence in which the s, p, d, and f orbitals are filled (see diagram, left) has essentially been determined by empirical means. Indeed, Bohr’s failure to derive the order for the filling of the orbitals has been described by some as one of the outstanding problems of quantum mechanics.…The problem is no longer the validity of Mendeleev’s system, but the best way to represent it.

NDLR. ** La validité du sytème de Mendéléev est-elle vraiment hors de question? La représentation serait-elle donc sans grande importance dans un système tel que celui de Mendeleev ? Un système représenté par un tableau est du fait même nécessairement associé à la topologie, à la géométrie et à la théorie quantique ; toutes disciplines que j’invoque dans le système du québécium. L’introduction d’une représentation nouvelle peut conduire à réviser cette théorie, encore aujourd'hui insuffisante. - Il n’y a pas un tableau idéal unique, une multitude de tableaux sont possibles qui sont scientifiquement corrects, mais inégaux devant notre besoin de comprendre la structure de l’atome et en particulier sa symétrie d’ordre 4. Le système du québécium et ses tableaux, à la différence de ce qui était admis jusqu’ici, mettent en évidence pour la 1re fois cette symétrie et proposent une compréhension meilleure de l’organisation de l’atome.

Réf. 3. 565) Système du Québécium. Patrick Callet 2014, À venir

Réf. 4. Maurice Kibler 2014. 563) Système du Québécium. Maurice Kibler 2014, Pierre Demers, Centenaire, lisulf.quebec/2_allocutionKibler.htm

563) Système du Québécium. Maurice Kibler 2014, Pierre Demers, Centenaire, lisulf.quebec/2_allocutionKibler.pdf

Réf. 5. Pierre Demers 2010, http://lisulf.quebec/ObtenirACFAS30XI2010.htm

Réf. 6. Eric Scerri, http://www.chem.ucla.edu/dept/Faculty/scerri/