3e de 4 communications pour le XIVe congrès international de biologie mathématique.
Paris, 9, 10 et 11 septembre 1993.
Revue internationale de biomathématique, XXXII, 2e trimestre 1994, No 126, 35-46
Nouvelle analyse de l'échelle musicale
des particules fondamentales
Pierre Demers, Centre québécois de la Couleur
Résumé. On rappelle que la distribution des masses des particules fondamentales s'accorde sensiblement avec deux invariances d'échelle établissant un parallèle avec la théorie de la musique : 1o le facteur d'échelle est le nombre 2; 2o le facteur d'échelle est la racine douzième de 2, ègale à l'intervalle diatonique de la gamme musicale tempérée. 3o On examine dans quelle mesure l'adoption des intervalles musicaux utilisées dans d'autres gammes peut améliorer cet accord. 4o Cette invariance d'échelle signifie que les degrés de cette distribution sont proportionnels au logarithme des masses. Un parallèle se présente dès lors avec la théorie de l'information, dans laquelle le nombre de bits d'information est proportionnel au logarithme des probabilités. Dans la théorie statistique de la matière, les probabilités sont égales à un nombre de complexions parmi lesquelles un choix a été réalisé. On cherche à interpréter ce parallèle.
15 particules fondamentales
Ce travail continue celui qui fut présenté au XIIIe Congrès et publié dans notre Revue. L'analyse porte sur 15 particules qui apparaissent comme plus fondamentales que les autres et qui sont chargées électriquement. Par ordre des masses croissantes, elles vont de l'électron e± au boson de jauge W±. Deux particules de même masse sont comptées pour une seule si elles ne différant que par le signe de leur charge électrique, comme c'est le cas pour l'électron et le proton. Rappelons que Louis de Broglie, dans son premier travail, posa comme principe que chaque masse possède une énergie mc
2 selon la relation d'Einstein et une fréquence f selon la relation de Planck. (1)f= mc2/h c célérité de la lumière, h constante de Planck
De la sorte, il est indifférent de parler des rapports mutuels des masses, des rapports mutuels des énergies ou des rapports mutuels des fréquences.
Si on évalue les masses en millions d'électron-volts Mev, voici la relation donnant numériquement la fréquence en hertz Hz.
f = 0,409.62 m 269 m en Mev
Si on fait apparaître la masse en unités valant la masse de l'électron soit 0,511 Mev :
f = 428,7 (m/0,511) 258 m en Mev
Au facteur 258 près représentant 58 octaves, la fréquence de l'électron est 428,7 Hz, voisine du la normal qui vaut 440 Hz.
Exemples d'invariances
La physique contemporaine doit beaucoup de ses progrès à la mise en oeuvre des notions de symétrie et d'invariance. On retrouve ces notions dans une foule d'exemples tirés des mathématiques élémentaires de la vie courante. L'exemple le plus immédiat peut être tiré de notre propre humanité. Dans l'opération de symétrie qui consiste à passer de l'un de nous à un autre, quelquee chose reste le même, c'est ce qui nous fait tous ressembler l'un à l'autre : le langage, une tête, deux bras, deux jambes, etc, en nous bornant aux caractères les plus évidents. Par ailleurs on note des différences de grosseur, de hauteur, de chevelure, et bien d'autres. L'invariance est à la fois véritable et incomplète. Entre l'aspect physique de tous les humains existent une différence d'échelle et en même temps une ressemblance ou ce que nous pouvons appeler une invariance d'échelle, elle aussi incomplète. Dans la structure du corps humain, il y a une symétrie entre la gauche et la droite, mais incomplète puisque le coeur est à gauche.
Considérons des triangles équilatéraux, qui sont des fictions oeuvres de notre imagination, et passons d'un tel triangle à un autre plus grand. Ils différent par leur côté mais c'est là leur seule différence : entre eux existe une rigoureuse invariance d'échelle.
Si l'on examine certains objets de l'art sériel tels que ceux du défunt Andy Warhol, on trouve un grand nombre de fois la représentation d'un même objet, mais pas tout à fait idenique à lui-même à chaue fois. C'est ce qu'on observe dans son célèbre "210 bouteilles de Coca-Cola", qui a rapporté 2,1 millions de dollars américains à leur propriétaire. L'opération de symétrie est le passage d'une case à l'autre, l'invariance est encore une fois véritable et incomplète. L'invariance est accompagnée d'une certaine diversité. Les chefs-d'oeuvre de l'architecture fournissent dans leurs structures des exemples de ces trois principes : symétrie, invariance et diversité.
La physique des particules a connu des progrès extraordinaires par l'exploitation de ces trois notions. La symétrie et l'invariance du groupe SU3 et d'autres groupes encore ont permis de prévoir l'existence et les propriétés plusieurs particules, mais elles sont imparfaites, et on parle alors de théories de jauge. Un très grand problème de symétrie imparfaite concerne l'abondance des protons positifs et des électrons négatifs. Comment expliquer l'absence apparente dans l'Univers d'une égale proportion de protons négatifs et des électrons positifs?
La musique présente un exemple particulièrement intéressant pour nous d'une invariance d'échelle. À tous les facteurs 2 exercés sur une fréquence audible donnée, on retrouve une perception musicale analogue : un do1 devient un do2. Un air transposé d'une quinte c'est-à-dire dont toutes les fréquences sont multipliées par un facteur voisin de 3/2, sonne pareil à nos oreilles. On dira qu'un son musical est invariant d'échelle sous l'opération de symétrie qui consiste dans ces transpositions, le facteur d'échelle étant tantôt le facteur 2 ou le facteur 3/2. Encore une fois, la symétrie est imparfaite et la transposition donne un résultat qui se discerne de l'original, la preuve étant que précisément on éprouve le besoin de transposer pour les fins de l'art.
La série des sons musicaux elle-même fournit un exemple d'invariance. Lorsqu'on passe d'une fréquence de cette série à la suivante, quelque chose reste constant et invariant : c'est la qualité d'appartenir à la collection des sons admis dans le cadre de la convention musicale, disons de la gamme choisie; les fréquences étrangères sont exclues, elles sont fausses. Et pour réaliser cette invariance, on trouve la foule des règles anciennes et modernes des tons, des semi-tons, des demi-tons, qu'ils soient majeurs ou mineurs, diésés ou bémolisés, doublés ou triplés ou bécarre, etc.
Une règle rigoureuse et universelle semble se maintenir à travers l'histoire de la musique : c'est la règle d'octave. Au bout de la gamme se trouve invariablement, c'est le cas de parler d'une invariance, l'octave de facteur 2. On peut assurément rattacher ce facteur 2 à des exigences de géométrie et de mécanique vibratoire. On pourrait philosopher sur l'importance de ce facteur 2 qui survient en musique et en physiologie et la rapprocher de ce qu'on vérifie en théorie de la gravitation et de l'électromagnétisme : la valeur exacte de 2 intervient dans les formules, comme puissance affectant les dimensions spatiales. Déjà Faraday l'avait vérifié pour la loi de l'inverse du carré de la distance en élevctricité, et toute la mécanique céleste repose sur l'exactitude de la puissance 2 dans la loi de l'attraction universelle. On peut assurément rattacher cela à des raisons d'angle solide donc de géométrie.
Quant à l'invariance d'échelle correspondant au respect du caractère musical quand on passe d'une note à une autre dans une gamme déterminée, une autre règle émergea il y a 300 ans et ce fut un perfectionnement décisif, qui facilita les transpositions et qui donna un essor nouveau à la polyphonie. C'est alors que Jean-Sébastien Bach (1685-1750) fit admettre que la gamme serait formée de douze demi-tons égaux emplissant l'octave, chacun est appelé demi-ton diatonique et la gamme est la gamme tempérée. Le demi-ton diatonique de la gamme chromatique vaut par suite un facteur b.
L'invariance d'échelle en musique concerne les fréquences. L'équidistance des octaves et celle des degrés de la gamme(do, do#, ré, etc) concerne le logarihme des fréquences. Si on fait usage du logarithme base 2, l'équidistance des octaves est d'une unité à la fois, l'équidistance des degrés de la gamme tempérée est d'un douzième d'unité ou 0,083.333. Si on fait usage du logarithme base b, l'équidistance des
octaves est de douze unités et l'équidistance des degrés de la gamme tempérée est d'une unité.L'invariance d'échelle se distingue de ce qu'on peut appeler l'invariance arithmétique. Ainsi un mur de briques égales, une page emplie de lignes équidistantes présente une sorte d'invariance ou de régularité, mais qui mérite l'épithète d'arithmétique : un rang, une ligne s'obtient à partir de l'élément précédent en ajoutant à ce dernier une hauteur additive. il y a progression arithmétique. Dans l'invariance d'échelle, il y a progression géométrique d'un degré au suivant, par l'application d'un facteur d'échelle, et les degrés deviennent égaux si l'on se sert de la fonction logarithme.
Première invariance d'échelle : le facteur 2
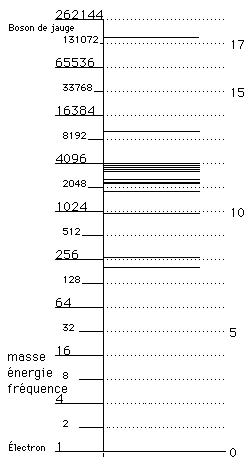
Voyons, dans le Tableau I, la description de nos 15 particules fondamentales.
Tableau I
Les particules fondamentales
(m/0,511), m masse, la masse de l'électron valant 0,511 Mev.
Classe Nom
3 leptons
électron e± (1)
muon µ± (206,77)
tau ± (3491,4)
1 boson de jauge
W± (157730)
11 hadrons
6 mésons
kaon K± (966,05)
pion π± (273,13)
D± (3658,1)
Ds± (3852,8)
Ds*± (4129,7)
beauté B± (10328)
5 baryons
proton p± (1836,15)
sigma ∑+ (2327,5)
sigma ∑- (2342,3)
xi
oméga
W (3272,9)
Ce sont là les particules chargées électriquement classées S (pour stables), en omettant les baryons charmés. Ces masses sont fort disparates, elles s'échelonnent entre 1 et 157730 et leur répartition, dans un premier examen, n'obéit à aucune régularité. Tout au plus peut-on remarquer une accumulation des masses au voisinage de celle du proton. Cependant, nous allons voir qu'une régularité apparaît dans cette distribution si nous examinons non les valeurs naturelles des masses mais leurs logarithmes. Nous utilisons le logarithme base 2, lequel vaut 3,321.928 fois le logarithme base 10. On reconnaît, au Tableau II, que les fréquences occupent 18 octaves. On rattache chaque valeur de X, égale à L
2(m/me±), au nombre entier le plus proche ou numéro d'octave K, qui reste compris entre 0 et 17.X = L
2(m/me±)K = entier(X + 0,5)
Tableau II. 15 particules fondamentales
logarithmes des masses : base 2 et base b = 2
1/12 = 1,059.463Dans la colonne "octave", on a inscrit l'entier K le plus proche du nombre dans la colonne précédente
| Nom |
Mev |
m/me± |
X L2(m/me ± ) |
K Octave |
D X |
Lb(m/me ± ) |
|
e± |
0,511 |
1 |
0 |
0 |
0 |
0 |
| µ± |
105,07 |
206,77 |
7,692 |
8 |
- |
92,30 |
| π± |
139,568 |
273,13 |
8,093 |
8 |
+ |
97,12 |
| K± |
493,696 |
966,05 |
9,916 |
10 |
- |
118,99 |
|
p± |
938,27 |
1836,15 |
10,842 |
11 |
- |
130,11 |
| S + | 1189,4 |
2327,5 |
11,185 |
11 |
+ |
134,22 |
| S - | 1197,4 |
2342,2 |
11,194 |
11 |
+ |
134,33 |
| X - | 1321,32 |
2385,8 |
11,337 |
11 |
+ |
136,04 |
| W - | 1672,43 |
3272,9 |
11,678 |
12 |
- |
140,12 |
| t ± | 1784,1 |
3491,4 |
11,77 |
12 |
- |
141,24 |
| D± |
1869,3 |
3658,1 |
11,837 |
12 |
- |
142,04 |
| Ds± |
1968,8 |
3852,8 |
11,912 |
12 |
- |
142,94 |
| Ds*± |
2110,3 |
4129,7 |
12,012 |
12 |
+ |
144,14 |
|
B± |
5277,6 |
10328 |
13,334 |
13 |
+ |
160,01 |
| W± |
80600 |
157730 |
17,268 |
17 |
+ |
207,21 |
Par invariance d'échelle facteur 2, nous voulons ici dire que les masses rapportées à celle de l'électron seraient toutes égales aux puissances de 2. En d'autres termes, les valeurs de X seraient exclusivement des entiers. Le Tableau II fait apparaître, si on examine les colonnes X et K, des différences évidentes entre X et K (dont le signe seul figure dans la colonne
D X = X - K).Analysons ces différences D X = X- K. Sept d'entre elles sont positives et sept sont négatives, et la moyenne de leurs valeurs est 0,005, ce qui suggère soit qu'elles sont réparties au hasard soit que l'électron joue un rôle normatif dans leur répartition. Par construction, ces valeurs de D X restent comprises entre -0,5 et +0,5, mais en fait, leur distribution est plus resserrée : entre -0,322 et+0,337. Les valeurs extrêmes de D x représentent, pour les masses, un écart d'un facteur compris entre 1/1,251 et 1,263. Si la distribution des différences D X était aléatoire, elle pourraient aller de -0,5 à +0,5, avec un facteur touchant 1/1,414 et 1,414; leur moyenne arithmétique serait 0,250 alors qu'elle est 0,191. Cette analyse suggère qu'il existe vraiment une tendance à ce que les masses se groupent autour des valeurs puissances entières de 2.
Un petit changement dans la valeur du facteur d'échelle pris égal à 2 augmenterait la valeur moyenne de D X. Cela suggère que cette valeur possède une signification particulière pour les particules fondamentales. La figure 1 montre la distribution par niveaux des valeurs de X. Elles se rassemblent au voisinage des valeurs entières K = 0, 8, 11, 12 13,

Fig. 1. Invariance d'échelle facteur 2 pour 15 particules. En ordonnées, les valeurs de X pour les 15 particules fondamentales.
Le facteur d'invariance de la gamme tempérée
Dans l'ordre du clavier musical,
les notes vont du fa au do# supérieur.Jean-Sébastien Bach fit franchir à la pratique musicale une étape considérable en adoptant la gamme tempérée, dans laquelle tous les intervalles sont des demi-tons égaux entre eux et au douzième de l'octave. La transposition ou changement de tonique devenait ainsi beaucoup plus facile qu'auparavant. L'intervalle diatonique ainsi défini vaut un facteur racine douzième de 2 ou 21/12. Désignons par la lettre b ce facteur.
b = 2 1/12 = 1,059.463.
Invariance d'échelle facteur b (gamme tempérée)
Rappelons que le nom des notes se répètent à chaque octave : un facteur deux ou puissance entière de deux ne change pas le nom d'une note. On peut toujours ramener une fréquence choisie, par réduction d'octaves appropriées, à l'intérieur d'une octave déterminée. C'est ainsi que nous pouvons décrire la fréquence f de l'électron comme voisine du la normal, car, à plusieurs octaves ou à plusieurs facteurs 2 près, cette fréquence vaut 428,7 Hz. Le la normal admis de nos jours vaut 440 Hz.

Fig. 2. Invariance d'échelle facteur b pour les particules fondamentales.
Une bonne manière de figurer cette comparaison est celle de la figure 2, où l'intervalle de l'octave occupe un cercle horaire, avec l'électron placé à midi. Le proton est au sol à 10 heures et le boson de jauge au do à 3 heures, etc. Avant d'apparaître dans cette figure, les fréquences ont été divisées par deux un nombre suffisant de fois pour les ramener dans les limites de l'octave renfermant la fréquence de l'électron prise comme la à 427,3 Hz.
Si l'accord était parfait, le rayon marquant chaque particule se placerait exactement sur l'une des positions horaires marquées par un pointillé. Chaque particule tomberait sur une heure juste et sur un demi-ton exact. On voit qu'il n'en est pas ainsi et les incertitudes sur les valeurs exactes des masses ne peuvent pas expliquer la totalité des écarts observés. Par exemple, pour le proton, l'écart est de 11 centièmes d'heure ou de demi-ton diatonique. Si l'on voulait faire apparaître cet écart en minutes, le proton serait représentépar deux aiguilles, l'une qui est figurée étant l'aiguille des heures, l'autre étant celle des minutes serait à la position de 6 minutes et 6 dixièmes après midi : en bref, le proton est à 10 heures et 6 minutes et semblablement, le boson de jauge est à 3 heures et 13 minutes, etc.
On peut mettre en évidence ces fractions de demi-ton marquant l'imperfection de l'accord entre les masses et les places exactes que l'invariance d'échelle leur assignerait. On peut tout autant s'étonner que l'accord ne soit pas plus imparfait, alors que le domaine des fréquences concernées touche 17 octaves. Cela veut dire que même pour le boson de jauge W±, la masse se fixe très près de l'un des degrés de l'échelle d'invariance, au sein d'une octave dont le la possède une fréquence valant 131.072 fois celle de l'électron.
Tout cela vaut pour les invariances d'échelle dans une gamme tempérée.
Cependant, la gamme tempérée fut précédée par des gammes de diverses descriptions donnant également 12 notes par octave, valant approximativement ceux de la gamme tempérée. Si l'on se réfère à l'histoire de la musique, on y apprend que la structure de ces gammes anciennes posait des problèmes qui excluaient certaines transpositions qui conduisaient à des discordances excessives, entre autres celles faisant passer de la tonalité en do à une tonalité en mi. Leur multiplicité rendait en outre impossible la musique symphonique parce que chaque instrument avait ses règles propres d'accord et d'exécution.
Il serait indiqué d'essayer de remplacer, dans l'octave de la figure 2, les intervalles diatoniques égaux par ceux, inégaux, de ces diverses gammes. Avant même d'avoir essayé ces remplacements, il paraît assez évident que l'une quelconque de ces gammes pourrait améliorer l'accord entre les fréquences des particules et l'échelle adoptée. Des remarques communiquées par Langlet
† au cours du XIVe congrès m'ont encouragé à réaliser les calculs requis.Gammes et intervalles
Rappelons que les gammes anciennes distinguaient dièses d'une note et bémols de la note supérieure, alors que la gamme tempérée les confond. Ces gammes comprenaient donc, en principe, 21 valeurs par octave.
Les gammes les plus connues sont celles de Pythagore qui procède par quintes successives et celle de Zarlino, qui fait usage des rapports d'entiers simples. Tous les rapports de fréquences de la gamme de Pythagore sont obtenus par les puissances successives de 3 ramenées à une octave unique. Prenons do1 pour tonique et procédons par quintes montantes. Le do supérieur est atteint à la puissance 12e et il est 1,36 % trop haut.
Tableau III Gamme de Pythagore
Quintes
|
Notes | Puissance de 3 | Rapports |
| do1 | 1 | 1 |
|
sol | 3 | 1,5 |
|
rè |
9 | 1,125 |
| la | 27 | 1,6875 |
| mi | 81 | 1,265625 |
| si | 243 | 1,8984375 |
| fa# | 729 | 1,423828125 |
| do# | 2187 | 1,06787109375 |
| sol# | 6561 | 1,601806640625 |
| ré# |
19683 | 1,20135498046875 |
| la# | 59049 | 1,802032470703125 |
| fa | 177147 |
1,3515243530273438 |
| do2 | 531441 |
1,0136432647705078 |
Dans la gamme de Pythagore, les fréquences obtenues pour chacune des notes de la gamme sont toutes systématiquement plus élevées que dans la gamme diatonique. Les écarts apparaissent dans la dernière colonne du Tableau IV, dans des unités telles qu'un demi-ton diatonique vaut 0,059.463
Tableau IV Gamme de Pythagore
fréquences croissantes
|
Quintes, do = 0 | Octave |
L2fréq."Q" |
D L2 ="Q" - Diaton. |
|
do | 0 | 0 | 0 |
|
do# | 7 | 0,09474 |
0,0114 |
| ré |
2 | 0,16993 |
0,00326 |
| ré# |
9 | 0,26466 |
0,01466 |
| mi | 4 | 0,33985 |
0,00652 |
| fa | 11 | 0,50978 |
0,00978 |
| fa# |
|
|
|
| sol | 1 | 0,58496 |
0,00163 |
| sol# | 8 | 0,6797 |
0,01303 |
| la | 3 | 0,75489 |
0,00489 |
| la# | 10 | 0,84963 |
0,01629 |
| si |
5 |
0,92481 |
0,00815 |
| do |
12 |
1,01955 |
0,01955 |
Tableau V
Déviations aux octaves dans les gammes de Pythagore
Octave de départ 1,000.00
| Octave |
Déviation |
| 1 |
1,013.64 |
| 2 | 1,027.47 |
| 3 | 1,041.49 |
| 4 | 1,055.70 |
| 5 | 1,070.10 |
| 10 | 1,145.12 |
| 20 | 1,311.30 |
| 40 | 1,719.51 |
| 60 | 2,254.80 |

Fig. 3. On montre les écarts entre la hauteur X dans la gamme de Pythagore et la hauteur dans la gamme diatonique. La hauteur selon Pythagore est trop élevée.

Fig. 4. Le do1 est à 0 heure midi. Un tour vaut une octave. Les hauteurs successives X apparaissent en fraction d'un tour pour la gamme de Pythagore. Les intervalles sont des demi-tons inégaux. Le do2 apparaîtrait à 0,1637 heure à droite de midi.
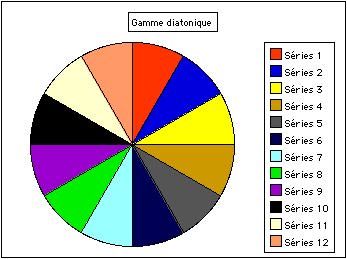
Fig. 5. Gamme diatonique. Tous les demi-tons sont égaux.
La valeur exacte de 2 est de la plus grande importance en physique classique et, nous l'avons reconnu ci-dessus, pour l'invariance facteur 2 des particules. Cela suggère de considérer avec méfiance une gamme telle que celle de Pythagore qui ne conduit pas à cette valeur exacte mais qui introduit une déviation de plus d'un pour cent à l'octave et presque un quart de ton après deux octaves. Les déviations aux octaves successives sont énumérées au Tableau V sous la forme d'un facteur.
Tableau VI
Gamme de Zarlino
| Z - d, L2 |
idemX12, Lb | |
| do = 1 |
||
|
do# = 15/16 ré | -0,00652 |
-0,07821 |
| ré = 9/8 | 0,00326 |
0,0391 |
| ré# = 15/16 mi | -0,02118 |
-0,25418 |
| mi = 5/4 | -0,01141 |
-0,13686 |
| fa = 4/3 | -0,00163 |
-0,01955 |
| fa# = 15/16 sol | -0,00815 |
-0,09776 |
| sol = 3/2 | 0,001629 |
0,01955 |
| sol# =15/16 la | -0,02281 |
-0,27373 |
| la = 5/3 | -0,01303 |
-0,15641 |
| la# = 15/16 si | -0,01955 |
-0,23463 |
| si = 15/8 | -0,00978 |
-0,11731 |
| do = 2 | -1 | 0 |
La gamme de Zarlino est fondée sur une série des nombres entiers, ramenés à un rapport entre 1 et 2. Cette fois, le do supérieur est atteint exactement.
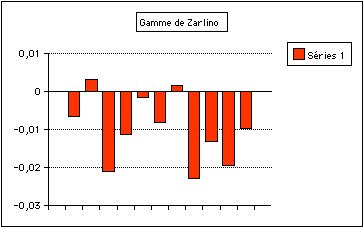
Fig. 6. Écarts entre les hauteurs dans la gamme de Zarlino et dans la gamme diatonique. Les hauteurs selon Zarlino sont trop basses sauf ré et sol
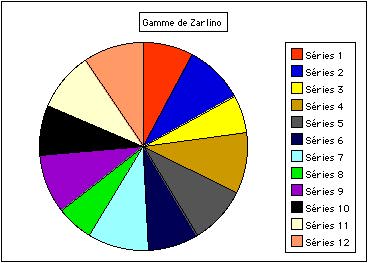
Fig. 7. Les hauteurs successives X apparaissent en fraction d'un tour pour la gamme de Zarlino. Les intervalles sont des demi-tons inégaux. Le do2 apparaît exactement à midi.