Il reste à savoir comment choisir les retournements des 4 quadrants dans chaque angle droit des strates. À priori, chaque quadrant peut intervenir sous le retournement de notre plaisir, et cela représente 256 possibilités pour une strate donnée. Par souci de symétrie, nous optons pour la diversité, de manière que les 4 retournements soient employés. À ce moment, il y a 24 possibilités. Plus symétriques que les autres, nous remarquons 2 options parmi les 24.

   1re option, option centrifuge. Les cases s sont aussi loin que possible du centre de figure.

   2e option, option centripète. Les cases s sont aussi près que possible du centre de figure, elles se touchent et tracent un carré. Figure 2.20.

Figure 2.20. Placements des quadrants dans une strate, 2 options.

   Dans ces 2 dernières options, les diagonales principales des quadrants tracent un X centré. Dans la 1re option, 28 cases f dessinent une croix centrale aux barreaux épais de 2 cases. Dans la 2e option, elles dessinent une couronne périphérique. Dans cette même 2e option, les cases utilisées restent jointives dans les quadrants obtenus par réduction des quadrants types, pour les strates autres que la 4e, ce qui n'est pas le cas dans la 1re option. Autre avantage - du point de vue symétrie et simplicité, de la 2e option, les cases de même dénomination forment une couronne alors que, dans la 1re option, les cases s, p et d forment des îlots disjoints.

   Pour ces raisons, nous préférons la 2e option, option centripète. Une sorte de loi de la nature semble l'imposer inévitablement.

   Une matrice 8X32. Adoptant la 2e option ci-dessus et utilisant les quadrants types, voilà la grille complète contenant la configuration du Québécium. Elle a 8 lignes, 32 colonnes et 256 cases, elle se divise en 4 strates (4 matrices strates) alignées horizontalement. La configuration y est décrite de façon abrégée et littérale seulement. Figure 2.21

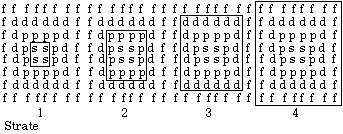
Figure 2.21. Matrice 8X32 de la configuration du Québécium. Termes en écriture littérale. Quadrants types. Les encadrements distinguent les quadrants réduits.

   Cette matrice se condense en un tableau par la suppression des cases inutiles. Le résultat est un tableau qu'on peut inscrire dans une matrice 8X20 de 160 cases, dont 40 non employées. Fig. 2.22.

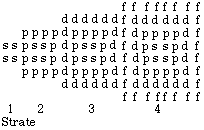
Fig. 2.22. Comme la figure 2.21, tableau. Quadrants réduits. 120 cases dont 2 vides.

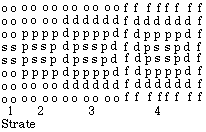
Fig. 2.23. Le tableau de la figure précédente inscrit dans une matrice 8X20 avec 40+2 cases vides.

   Dans les grilles des dernières figures, les numéros d'ordre des termes individuels croissent de gauche à droite. D'autres dispositions mutuelles des strates constituées sont possibles. Des exemples apparaissent à la figure 2.24, où les strates sont représentées schématiquement par des carrés de tailles différentes. Une disposition ramassée est particulièrement économique d'espace, elle s'inscrit dans une matrice 14X10 de 140 cases. Figure 24.

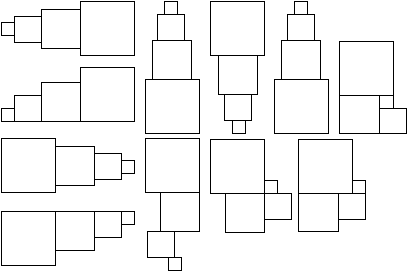
Figure 2.24. Diverses dispositions des strates.

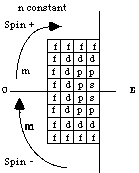
   Périodes. À l'intérieur des strates, il nous faut répartir les 4 quadrants entre les périodes composantes, de numéro pair ou impair. Chaque période répond à 2 quadrants, où les signes des spins sont opposés. À priori, 12 dispositions sont possibles, mais nous retenons seulement celle figurée ci-dessous. Les spins sont négatifs dans les quadrants O et positifs dans les quadrants E. Le 1er terme d'une période se trouve dans un quadrant O, le dernier, dans un quadrant E. Les 2 termes des orbitales se répondent dans des quadrants diamétralement opposés. Figure 2.25.

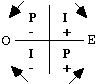
Fig. 2.25. Quadrants dans une strate. Période paire P, impaire I, spins - et +. Sens de rotation dans les équerres.

   Placements des termes individuels. Voilà donc comment la configuration du Québécium peut apparaître globalement à 2 dimensions, mais les termes individuels ne sont jusqu'ici identifiés que par leurs lettres s, p, d ou f. Il nous faut inscrire dans chaque case les caractères complets de chaque électron. Nous posons que le contenu d'un quadrant est fixe. Nous posons aussi que le contenu de chaque équerre est fixe et ordonné selon les valeurs du quantum magnétique m et du numéro d'ordre de l'électron.

   Sauf pour les équerres s, il nous faut choisir un sens de rotation pour cette mise en ordre et ce sens sera le même pour toutes les équerres d'un quadrant. 16 possibilités se présentent. Nous posons que ce sens sera le même pour les 2 quadrants opposés d'une période. De la sorte, les cases diamétralement opposées sont les termes d'une orbitale. Par symétrie, les sens de rotation seront opposés pour les périodes paires et impaires. Nous choisissons arbitrairement le sens des aiguilles d'une montre pour la période impaire. Figure 2.25. Exemple figure 2.26.

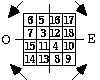
Figure 2.26. Rotations dans la strate 2.Numéros d'ordre des termes : 3 à 18.

2.3.7 Enchaînement des quadrants

   Voici une mise en évidence schématique des quadrants dans l'ordre des périodes et des numéros d'ordre des termes individuels. Toute période commence dans un quadrant - et se termine dans un quadrant +. Figure 2.27.

Figure 2.27.Enchaînement des 14 quadrants. Leur assemblage pour former les 4 strates.

2.3.8 Le quadrant type en couleurs

    Le quadrant type, avec ses 16 cases et ses 4 équerres, est à la base de la présentation bidimensionnelle de la configuration électronique du Québécium. Afin de faciliter son utilisation, nous colorons les cases des équerres : rouge, jaune, vert et bleu, R, J, V et B au lieu des lettres s, p, d et f respectivement. (On espère que l'information colorée parviendra jusqu'au lecteur). Les lettres dans les cases codées par ces couleurs deviennent redondantes. Voici l'aspect de ce quadrant en couleurs RJVB. Ce sont les 4 couleurs fondamentales non neutres. Fig. 2.28.

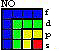
Figure 2.28.Quadrant type en couleurs RJVB.

   On s'efforce, dans cet ouvrage, de réserver l'usage des couleurs au symbolisme des valeurs du quantum azimutal l, à la synonymie avec les lettres s, p, d, f.

   Reprenons schématiquement, avec usage des couleurs, certaines des figures précédentes. 2 quadrants opposés représentent une période. Fig. 2.29.

Figure 2.29.Deux quadrants renfermant une période. Quadrants NO et SE. En carreaux de couleurs.

   Quatre quadrants s'associent pour former une strate. Figure 2.30.

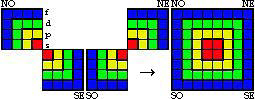
Figure 2.30. 4 quadrants renfermant 2 périodes, réunis en une strate de 4 couronnes.

   Un enchaînement de 14 quadrants représente la configuration. Figure 2.31.

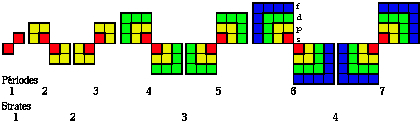
Figure 2.31. 14 quadrants représentant la configuration du Québécium. Largeur 40 carreaux, hauteur 8 carreaux.

   Quatre strates représentent la configuration. Figure 2.32

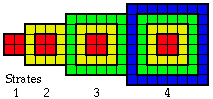
Figure 2.32. Les 4 strates, emboîtements résultant de la figure 2.31. On a ajouté 2 carreaux vides, total 120 carreaux.

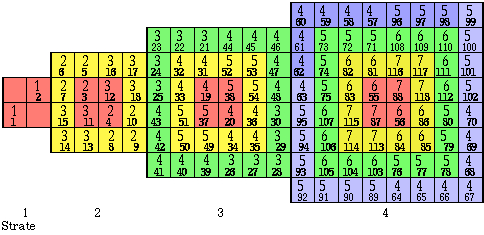
   Voici la représentation bidimensionnelle de la configuration du Québécium, figurant les termes individuels des 118 électrons. Figure 2.33.

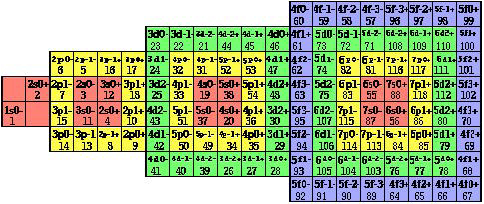
Figure 2.33. Représentation bidimensionnelle de la configuration électronique du Québécium. Dans chaque case : le caractère et le numéro d'ordre des 118 électrons. Les couleurs sont synonymes des lettres.

2.3.9 Redondances, codage simplifié

   Étant donné les conventions faites, l'écriture complète du quadruplet nlms dans une case est redondante et peut se simplifier au point de devenir un singulet ne renfermant que la valeur de n. Voici ces conventions et leurs conséquences. Elles établissent un contexte positionnel et coloré rendant superflue l'écriture du triplet (l, m, s) au sein du quadruplet (n, l, m, s). Tableau 2.8, figures 2.34, 2.35, 2.36.

Fig. 2.34 Quantum azimutal dans les cases de la strate type. Valeur.

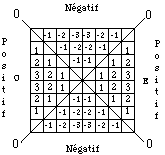
Figure 2.35 Quantum magnétique m dans la strate type. Signe et valeur.

Figure 2.36 Spin s dans la strate type. Signe.

   En écrivant dans les cases le singulet (n) au lieu du quadruplet (n, l, m, s). on a refait la figure 2.33. Figure 2.37.

Figure 2.37. Représentation synonymique de la configuration électronique du Québécium. Dans chaque case, le caractère, réduit au singulet (n) en tirant parti des synonymies, et le numéro d'ordre des 118 électrons. Les synonymies évitent d'écrire les valeurs de l, m et s. Cette représentation met en évidence les couches d'électrons.

2.3.10 Présentation par couches

    La considération de la figure 2.37 qui met enévidence les valeurs de n et par suite les couches d'électrons du Québécium suggère une présentation remaniée, oublieuse de l'organisation des sous-couches en périodes et en strates mais respectueuse des structures en équerres et de l'option centripète qui rassemble les cases s. Les équerres sont associées en matrices types 8X4 avec un sens de rotation unique. Figure 2.38.

Figure 2.38 Matrice type 8X4

   Le 1er terme des périodes est au sud, le dernier, au nord. Étant donné le codage, il suffit d'inscrire dans les cases les numéros d'ordre des termes. On obtient une présentation par couches. Figure 2.39.

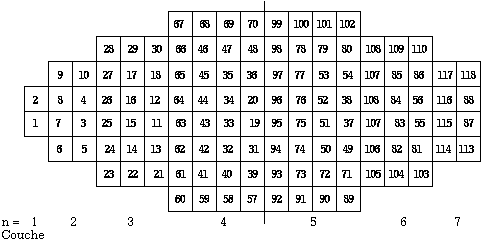
Figure 2.39 Configuration du Québécium par couches. On a inscrit les numéros d'ordre des termes.

2.4 La grille du Québécium.

    La présente analyse a fait apparaître la grille remarquable de la figure 2.33, qui rattache la configuration du Québécium à la théorie des matrices et à la géométrie du carré. Nous ne gardons dans les cases que les numéros d'ordre des termes. Nous appellerons cette grille la grille du Québécium. Elle est cotée en correspondance avec les numéros d'ordre des électrons du Québécium et elle nous servira plus tard. Figures 2.40, 2.41.

Figure 2.40. Grille du Québécium de 120 cases. 118 cases cotées par correspondance avec les électrons du Québécium, 2 cases restantes numérotées 119 et 120. Version en blanc et noir.

Figure 2.41. Grille du Québécium de 120 cases. 118 cases cotées par correspondance avec les électrons du Québécium, 2 cases restantes numérotées 119 et 120. Version en couleurs.

2.5 Des équerres, des carrés et des quantifications

2.5.1 Un résumé de la logique

    Équerres. Les équerres symétriques géométriquement sont liées aux nombres de valeurs permises du quantum magnétique m, nombres impairs.

   Carrés. Que ces équerres s'emboîtent exactement sans lacune pour chaque sous-période est une quantification remarquable, correspondant à la complétude des sous-couches dans les sous-périodes.

   Pairage des orbitales. Que ces équerres et ces carrés se présentent par paires dans une période correspond au pairage dû aux deux valeurs - et + du quantum de spin doublant des termes autrement uniques.

   Pairage des strates. Que les périodes après la première se présentent deux par deux avec les mêmes longueurs et les mêmes configurations est une autre quantification remarquable que nous avons appelée stratification.

   Nombres pairs et impairs interviennent dans ces quantifications pour structurer la configuration du Québécium après la 1re période en grilles carrées. En bref ci-dessous.

      m nombres impairs 1, 3, 5, 7, complétude -> équerres, carrés, carrés d'entiers.

       s nombre pair 2 -> facteur 2.

       2 nombre pair -> stratification -> facteur 2.

      Ces deux derniers facteurs -> facteur 4.

2.5.2 Quadruplets d'électrons