2.6.7 Coordonnées non trirectangles. Trois angles obliques
Afin d'étudier commodément la répartition des termes du Québécium dans les cases sphériques du tétraèdre, il nous faut choisir un système de coordonnées adapté aux files de boules issues de l'une d'elles occupant un sommet. Examiné avec l'habitude des coordonnées cartésiennes, un tel tétraèdre est déroutant. Les files de boules font entre elles des angles de 60o. Le système de coordonnées peut se symboliser ainsi. Figure 2.58.
R0O3[xy, zx, zy (phi = 60o)
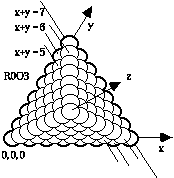
Figure 2.58. Axes de coordonnées triobliques R0O3 pour accommoder l'empilement tétraédrique. Les équations représentent les files de boules de la sous-couche f.
Le paramètre k est sans intérêt ici, parce qu'il ne s'agit pas de déplacer les strates l'une par rappport à l'autre, mais de coter les positions des termes dans les cases ayant forme de boules. Les coordonnées sont celles du centre des boules et elles ne prennent que des valeurs entières et positives comprises entre 0 et 7. Par exemple, le long de l'axe des z c'est à dire de l'arête montante à gauche dans la figure 2.58, x et y sont nuls pour toutes les cases. x = y = z = 0 représente la case origine des coordonnées à l'extrême gauche en bas. L'arête opposée pourvue de 8 boules répond à l'équation x+y = 7 d'une droite dans le plan z = 0.
Dans les représentations bidimensionnelles et tridimensionnelles par quadrants et coordonnées trirectangles, l'algorithme des couronnes avec correspondance aux couleurs et aux valeurs de l s'imposait pour raisons de symétrie et de simplicité. Les mêmes raisons appliquées à la représentation actuelle en coordonnées triobliques et en strates brisées en deux étages suggèrent de ne pas se contenter des répartitions de la figure.2.57, et de trouver mieux que la régularité des formes en équerres obliques reliquat des représentations précédentes. Une exigence persiste : les strates doivent garder mêmes compositions globales. La répartition des termes reste à ajuster.
Voilà ce qu'on a trouvé : placer les termes semblables sur des droites x+y = C = constante. La constante C peut prendre 8 valeurs. Il se trouve que cette ordonnance reçoit correctement tous les termes de chaque strate. Figure 2.59.
Sous-couche f B C = 6, 7 Étage impair; C = 5, 6 Étage pair
Sous-couche d V C = 4, 5 Étage impair; C = 3, 4 Étage pair
Sous-couche p J C = 2, 3 Étage impair; C = 1, 2 Étage pair
Sous-couche s R C = 0, 1 Étage impair; C = 0 Étage pair
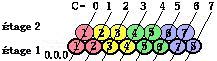
Figure 2.59. Valeurs de C pour les files. Nombre de boules dans chaque file. Vue latérale selon l'axe des x. Attribution des files aux 4 types de sous-couches R, J, V, B dans les 2 étages d'une strate, la strate 4 prise comme strate type.
Ces choix déterminent les nombres voulus de cases pour les sous-couches de la strate.
Les équerres sont devenues des files rectilignes de boules, 4 files sauf 3 dans la sous-couche s. Les files de chaque sous-couche forment un ensemble continu et, de plus, les files de même valeurs de l forment un ensemble continu, allongé selon la droite x+y = constante pour les groupes f et d et selon l'axe des z pour les groupes p et s. Ces paires de groupes concrétisés peuvent s'éloigner ou se réassembler à volonté. Il est frappant de voir que les groupes s et f sont à angle droit mutuellement. Figure 2.60.
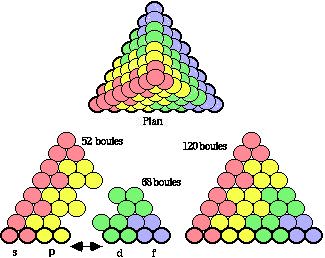
Figure 2.60. Groupes sp, df assemblables et démontables.
Dans une strate, les files de 2 étages s'associent pour recevoir les termes de chacune des périodes, selon une disposition en X reconnaissable sur les figures 2.59 et 2.61.
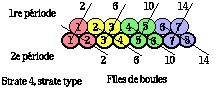
Figure 2.61. Alternances des files et des périodes. Division des files entre les périodes d'une strate. 2, 6, 10, 14, nombres de boules dans les sous-couches.
Tétrades. Les files de chaque sous-couche renferment un nombre entier de fois 4 boules. Cela rappelle la structure en paires d'orbitales notée dans une section précédente.Une paire de cette sorte est mise en évidence, qui comprend les termes de numéros 6, 9, 14 et 17. Nous appelons tétrade un tel groupe de 4 termes. Une tétrade de termes est définie par le numéro d'ordre électronique le plus petit qu'elle renferme dans la formule du Québécium.La tétrade 1 est incomplète. Figure 2.62.
Voici la liste des tétrades.
1, 3, 5, 6, 7, 19, 21, 22, 23, 24,
25, 31, 32, 33, 55, 57, 58, 59, 60, 61,
62, 63, 71, 72, 73, 74, 75. 81, 82, 83

Figure 2.62. Tétrades de termes et paire d'orbitales, termes ayant tous la même formule abrégée lm au sein d'une strate. Ici lm s'exprime par p0. Le numéro d'ordre électronique de cette tétrade est 6. Son numéro d'ordre de rangement est 2 dans la sous-couche p de la strate 2.
Les tétrades de boules sont évidentes dans les sous-couches s à la figure 2.60. Dans les autres sous-couches, on peut discerner les groupes de tétrades de boules. Chaque tétrade de boules résulte de l'association jointive de 4 boules, les unes ayant 3 boules en bas et les autres 3 boules en haut. De la sorte, elles garnissent la strate de deux étages. Les tétrades latérales marquant x = 0 ou y = 0 ont obligatoirement 3 boules en bas. Le tétraèdre entier renferme 30 tétrades.
2.6.8 Tétraèdre du Québécium. Structuration
L'organisation du tétraèdre suggère d'assigner à chaque tétrade de termes une tétrade de boules et la question se pose de les placer dans les files de chaque sous-couche. C'est ce que nous appelons la structuration du tétraèdre. Dans une recherche d'optimisation, un principe s'offre à nous : placer la tétrade renfermant le terme final des 2 sous-couches de la strate dans la position centrale. Il existe invariablement une telle position, puisque chaque sous-couche renferme un nombre impair de fois 4 termes. Poursuivons : quant aux sous-couches p, il faut bien placer la 1re tétrade d'un côté et la 2e, de l'autre côté. Nous adoptons l'ordre des coordonnées x croissantes. Pour les autres sous-couches, nous choissons le va et vient. Ainsi, pour les diverses sous-couches, voici les numéros d'ordre des tétrades, valable pour toutes les strates. L'ordre est ici celui du rangement des tétrades à l'intérieur d'une sous-couche.
f 1, 3, 5, 7, 6, 4, 2
d 1, 3, 5, 4, 2
p 1, 3, 2
s 1
À l'intérieur d'une tétrade, l'ordre d'inscription suit les valeurs décroissantes de z, puis les valeurs croissantes de x pour les tétrades impaires et inversement pour les tétrades paires.
Les principes ci-dessus sont compatibles entre eux et conduisent à la confection d'un tableau structuré pour la sous-couche f, où l'on montre les étapes suivies, puis du tableau global pour les 4 strates. Figures 2.63, 2.64, 2.65, 2.66.
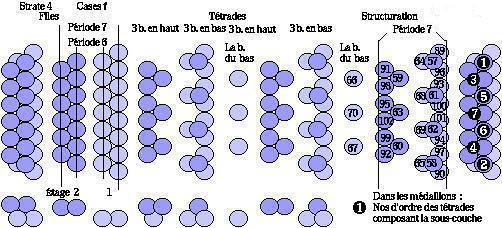
Figure 2.63. Numéros d'ordre des électrons du Québécium dans les cases f de la strate 4 prise comme strate type.
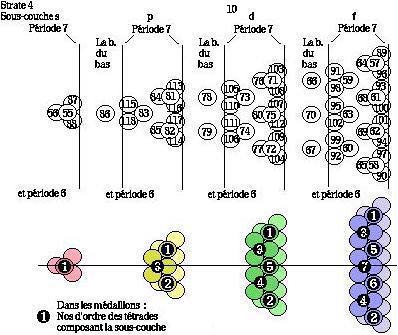
Figure 2.64. Structuration globale du tétraèdre. Les 4 strates, les 19 sous-couches.- Strate 4.
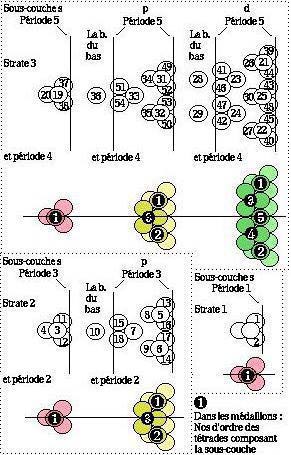
Figure 2.65. Structuration globale du tétraèdre. Les 4 strates, les 19 sous-couches.- Strate 3, 2, 1.
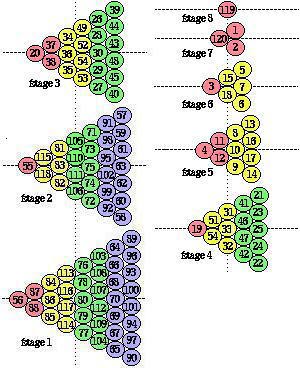
Figure 2.66. Structuration globale du tétraèdre. Les 8 étages.
Précédent
Suivant
Introduction
Chapitre
1
Chapitre 2
Chapitre 3
Chapitre 4
Chapitre 5
Chapitre 6
Dernière mise
à jour
: 4 novembre
2000








