L'axe des Z se trouve finalement incliné à 45o par rapport au plan XY. Chaque boule intérieure est supportée par 4 boules du plan inférieur. Outre ces 4 boules, elle touche 4 boules dans son plan et 4 autres dans le plan supérieur. Au total, elle touche 12 voisines. Cette organisation, faisant partie de la pyramide tétraédrique, est la même que celle de la pyramide à base carrée de la figure 2.54. Il n'y a pas de différences entre l'organisation mutuelle des boules dans l'une et l'autre pyramide, seulement des différences de présentation. Figure 2.67.
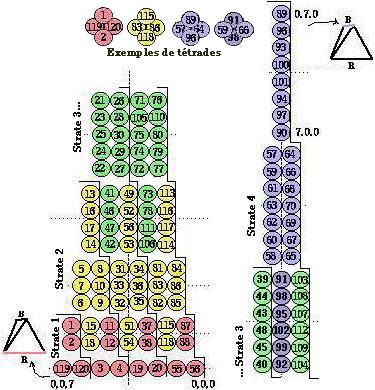
Figure 2.67. Plans x+y = C ou Z = constante. L'arête x+y = 0 est dans le plan du papier.
2.6.10 Polyèdres au lieu des boules
Dans le tétraèdre du Québécium, chaque boule intérieure est au contact de 12 boules. Par le point de contact, on peut faire passer un plan, soit 12 plans dont les intersections déterminent les arêtes et les sommets d'un polyèdre à 12 faces. À la différence du dodécaèdre régulier dont les faces sont des pentagones, le présent polyèdre, dodécaèdre lui aussi, a des faces en losanges. Ces faces ont des diagonales qui sont entre elles comme 1 et 21/2. Elles se rencontrent en arêtes faisant un angle dièdre de 120o. Elles forment 2 types de sommets : 3 par 3 aux rencontres des angles obtus des losanges, et 4 par 4 aux rencontres des angles aigus des losanges, soit 4 sommets 3 et 4 sommets 4. La projection montre un contour hexagonal selon la diagonale joignant 2 sommets 3 opposés, et un carré selon la diagonale joignant 2 sommets 4 opposés. Figure 2.68.

Figure 68. Vues du polyèdre. La boule inscrite. Une face du losange.
Pour réaliser l'étage 1 avec les polyèdres, on les fait tenir sur la table par un sommet 3. Ils s'assemblent par des faces au contact contenant la verticale. 3 polyèdres ainsi assemblés tels que (0, 0, 0). (1, 0, 0) et (0, 1, 0) présentent vers le haut une forme creuse qui épouse la forme d'un sommet 3. Ainsi peut-on poser un polyèdre 1, 0, 0 et commencer l'étage 2. Figure 2.69.
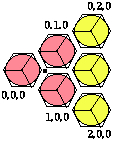
Figure 2.69. Polyèdres au lieu des boules. Portion de l'étage 1 du tétraèdre du Québécium, vue en projection verticale. Les polyèdres s'assemblent par des faces contenant la verticale. Ils reposent sur la table par des sommets 3. Le point noir : où poser le polyèdre 1, 0, 0.
2.6.11 Strates sous la forme de tétraèdres
Telles qu'elles se présentent dans le tétraèdre du Québécium, les strates après la 1re sont des troncs de tétraèdre. Le contenu des strates individuelles et des strates groupées 2 par 2 se prêtent. par des réarrangements des tétraèdres, à des représentations par des structures continues dessinant des tétraèdres, certaines d'entre elles massives et d'autres, à claire-voie. Elles possèdent les symétries du tétraèdre régulier. De ces structures, les tétrades sont des blocs constitutifs inaltérables. Des exemples apparaissent aux figures 2.70 à 2.73. Ces structures, sauf celle de 36 boules, dérivent de celle du tétraèdre du Québécium par suppressions de tétrades et permutations des tétrades restantes avec préservation de leur contenu.
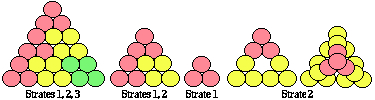
Figure 2.70. Tétraèdres dessinés par les strates 1, 2 et 3, 56 boules, 14 tétrades; par les strates 1 et 2, 20 boules formant un vingtain, 5 tétrades; par la strate 1, 4 boules, 1 tétrade; vues d'une face. Par la strate 2 isolée; vue d'une face et vue plongeante. Cette dernière structure est la même que celle du vingtain avec suppression de la tétrade centrale. Elle renferme 16 boules formant un seizain et 4 tétrades.
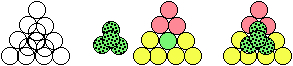
Figure 2.71. Structure tétraédrique dessinée par 36 boules, 9 tétrades de la strate 3. Cette structure résulte de l'addition à celle de 20 boules de 4 tétrades, une sur chaque face. Vue d'une face complète, de la tétrade isolée marquée en granulé, et de celle-ci mise en place. Elle ne dérive pas du tétraèdre du Québécium par suppression de tétrades.

Figure 2.72. Tétraèdre dessiné
par la strate 4.
Sa structure résulte de 4
fois la structure de la strate 2, soit 4 seizains de boules.
À gauche, le seizain supérieur isolé, à droite, en place. Vues en plan.

Figure 73. Vingtain structuré comme celui de la figure 2.70. Tétraèdre dessiné
par les strates 2 et 4 résultant de la structure de la figure 2.72 en quatre seizains augmentés chacun d'une tétrade ajoutée, soit de 4 vingtains. Vue en plan. Des tétrades ajoutées, celle dans le vingtain du haut est rouge, les autres sont jaunes.
2.6.12 Cube circonscrit au tétraèdre
Un tétraèdre régulier s'inscrit dans un cube, chacune de ses arêtes occupant une diagonale sur une face du cube : 6 arêtes au tétraèdre, 6 faces au cube. L'arête du cube vaut l'arête du tétraèdre divisée par 21/2. Figure 2.74.
L'installation d'un tétraèdre de boules dans une boîte cubique transparente posée sur une table permet d'observer commodément toutes les faces et d'apercevoir la projection verticale du tétraèdre. On remarque alors que l'arête supérieure et l'arête inférieure de celui-ci apparaissent croisées à angle droit et que les boules paraissent disposées en équerres occupant un carré. Si le tétraèdre est celui de 4, 16 ou 64 boules jointives des figures précédentes, chaque boule est visible au moins en partie. Puisque le cube a 6 faces, il y a 6 projections distinctes du tétraèdre. Figure 2.75.
Chapitre 3
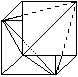
Figure 2.74. Aperçu d'un tétraèdre inscrit dans un cube.
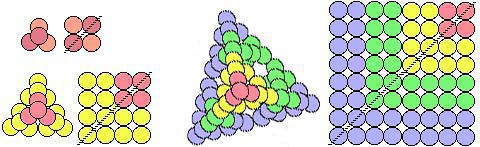
Figure 2.75. Projection verticale d'un tétraèdre
de boules inscrit dans un cube. Une tétrade, un seizain,
un 64-ain;. Un pointillé marque la
diagonale supérieure.
Les projections des boules sont espacées afin
qu'aucune n'en masque une autre.
1 -> 1 et 3;
3 -> 5 et 7;
5 -> 9 et 11;
7 -> 13 et 15.
De la sorte, chaque équerre doublée
remplace une couronne de la figure 2.30.
Précédent
Suivant
Introduction
Chapitre
1
Chapitre 4
Chapitre 5
Chapitre 6
Dernière mise
à jour
: 4 novembre
2000