2.13
Symétries
Les
formes géométriques
figurant la formule
électronique du
Québécium à 2
et à 3 dimensions
possèdent des
symétries nombreuses. Les
symétries peuvent être
purement géométriques
et porter exclusivement sur les
positions mutuelles des cases.
Elles peuvent être en outre
physiques au moins en partie, selon
le contenu des cases. Elles ne sont
jamais physiques
complètement à la
manière des symétries
cristallines, où les
mêmes atomes et les
mêmes ions se retrouvent
indéfiniment à
intervalles réguliers.
À la 1re strate, nous
attribuons 4 cases dont 2 vides,
présentes pour la
géométrie seulement
et colorées en rouge par
convention.
2.13.1
Symétries à 2
dimensions
Tableau d'ensemble. Le tableau
d'ensemble figure 2.37
possède un axe de
symétrie horizontal. Cette
symétrie persiste si on
permute l'ordre des strates
individuelles, si on les fait
glisser sur l'axe et si on les fait
tourner dans leur plan de
90o,
180o ou
270o.
Identifions physiquement les cases
par les nombres quantiques
principaux n. La symétrie
disparaît, parce que les
demi-périodes d'une
même période sont en
diagonale par rapport à
l'axe et non en regard.
Igentifions
les cases par leurs couleurs
conventionnelles. La
symétrie persiste, ce qu'on
peut rattacher à la
structure en couronnes. Si on
identifie les cases par la valeur
de l, l'axe disparaît parce
que les cases occupées de la
1re strate ne sont pas en
regard.
Ces divers résultats restent
inchangés si on identifie en
outre les cases par la valeur de m
et par le signe du spin. Figure
2.76.
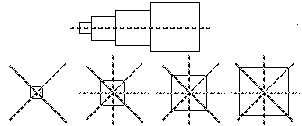
Figure 2.76. Symétries 2D.
En haut : un axe de symétrie
dans le tableau du
Québécium. En bas : 4
axes de symétrie dans les 4
strates individuelles; les axes de
rotation ne sont pas
figurés.
Strates individuelles. Les
strates individuelles
présentent les
symétries d'un carré,
savoir 4 axes, un horizontal, un
vertical et 2 diagonaux et en
outre, 2 axes de rotation, l'un
binaire et l'autre
quaternaire.Figure 2.76.
Identifions
les cases par les valeurs de n :
les axes diagonaux et l'axe de
rotation binaire
persistent.
Identifions les cases par les
couleurs conventionnelles. Les
symétries persistent, ce
qu'on peut, encore une fois,
rattacher à la structure en
couronnes.
Identifions
les cases par les valeurs de l.
Pour les strates 2, 3 et 4, toutes
les synétries notées
persistent. Pour la strate 1, les
symétries persistent pour
les axes diagonaux et pour l'axe de
rotation binaire. Figures 2.76 et
2.77.
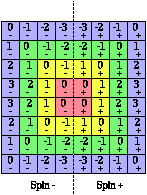
Figure 2.77. Strate type. Ici
apparaissent les couronnes
correspondant aux valeurs de l,
quantum azimutal, les valeurs de m,
quantum magnétique et le
signe du spin. On reconnaît,
en faisant abstraction du signe,
que les 4 quadrants se
répondent avec les 6
symétries décrites
dans le texte. Si on tient compte
du signe, seul subsiste l'axe de
symétrie horizontal.
Ces résultats
persistent si on identifie les
cases aussi par les valeurs de m.
Si on les identifie en outre par le
signe du spin, seules subsistent
les symétries notées
par rapport à l'axe
horizontal.
2.13.2 Symétries
à 3 dimensions
Symétries du
tétraèdre
régulier :
il n'a pas de
centre de symétrie; il est
notoire que le
tétraèdre
régulier est le seul parmi
les 5 solides de Platon à ne
pas posséder un centre de
symétrie; il a cependant un
centre de
figure;
4
axes de symétrie ternaire
passant par un sommet et le
centre;
3 axes
de symétrie binaire
perpendiculaires chacun à 2
arêtes opposées et
passant par le
centre;
6
plans de symétrie passant
par une arête et par le
centre.
Ces
symétries se manifestent
commodément lorsque le
tétraèdre est inscrit
dans un cube. Le cube
possède toutes les
symétries du
tétraèdre et en
outre, un centre de symétrie
et certaines symétries
binaires et quaternaires.
Tétraèdre du
Québécium. Le
tétraèdre du
Québécium
possède toutes les
symétries du
tétraèdre
régulier. Figures 2.78, 2.79
et 2.80.

Figure 2.78. Pour les
symétries 3D du
tétraèdre du
Québécium. L'axe des
z passe par l'enfilade de boules
rouges.
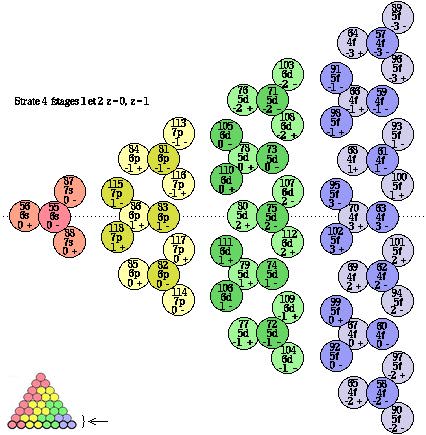
Figure 2.79. Strate 4 du
tétraèdre du
Qtébécium.
Caractères des
électrons au complet. Les
tétrades sont
éclatées afin de
laisser voir les boules de
l'étage inférieur de
la strate.
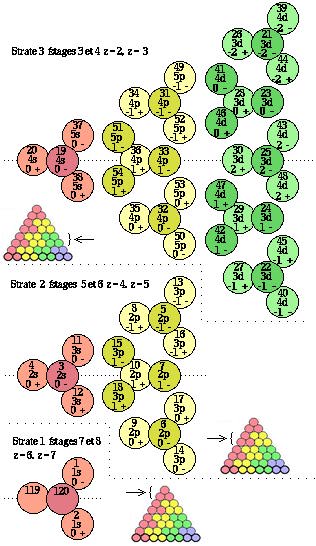
Figure 2.80. Strates 3, 2, 1 du
tétraèdre du
Qtébécium.
Caractères des
électrons au complet. Les
tétrades sont
éclatées afin de
laisser voir les boules de
l'étage inférieur de
la strate.
Toutes ces
symétries disparaissent si
on identifie les boules par la
valeur algébrique de
m.
En revanche, si on
identifie les boules par les
valeurs absolues de m, plusieurs de
ces symétries persistent,
comme suit.
Si on identifie les
boules par les valeurs de n, nombre
quantique principal, il persiste
:
un plan de
symétrie passant par l'axe
des z et par le centre.
Si on identifie les
boules par les couleurs
conventionnelles, il persiste :
un axe de
symétrie binaire
perpendiculaire à l'axe des
z et passant par le centre;
2 plans de
symétrie. l'un passant par
l'axe des z et par le centre,
l'autre perpendiculaire à
l'axe des z et passant par le
centre.
Si on identifie
les boules par les valeurs de l, il
persiste :
un
plan de symétrie passant par
l'axe des z et le centre.
Strates mises en
structures
tétraédriques. Ces
structures possèdent toutes
les symétries du
tétraèdre
régulier. Figure
2.81.
Certaines de ces
symétries persistent si on
identifie les boules par la couleur
et la valeur de l, comme suit.
Toutes ces
structures ont au moins :
un plan de
symétrie passant par une
arête et le centre.
Quant
aux structures B et C, elles ont
:
au total 3
plans de symétrie passant
par une arête et le
centre:
un
axe de symétrie ternaire
passant par le sommet des boules
rouges et par le centre.
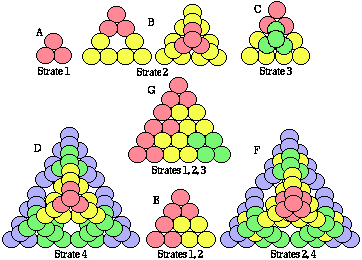
Figure 2.81. Pour les
symétries 3D dans les
strates mises en structures
tétraédriques. Rappel
de figures
précédentes. Vues
diverses.
2.14 Pentaèdre
du Québécium
Si,
du tétraèdre du
Qtébécium, on
ôte les 2 boules vides de la
strate 1, cettte disparition
équivaut à une
troncature faisant apparaître
une face et transformant le
tétraèdre en un
pentaèdre. La face nouvelle
est triangulaire, elle est
définie comme portion du
plan tangent à 3 boules, de
centres (0, 0, 5), (1, 0, 6), (0,
1, 6). Figure 2.82.
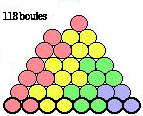
Figure 2.82. Pentaèdre du
Québécium. 118
boules. Vue d'une face.
2.15 Une tétrade
à 2 et à 3
dimensions
Nous
envisageons une tétrade
à 2 dimensions de 4 objets,
des boules par exemple, que, pour
la commodité de la
présente discussion, nous
identifions par les 4 couleurs r,
j, v et b, sans relation avec les
valeurs du quantum azimutal. Nous
les disposons en matrice
carrée 2X2. Sans perdre la
généralité de
ce qui suivra, nous fixons la
position de la boule r. Il y a 6
configurations possibles non
superposables l'une sur l'autre par
une rotation dans le plan.
Nous
formons de ces mêmes boules
une tétrade à 3
dimensions. Nous supposons les 4
boules fixées à 4 des
sommets d'une boîte cubique
transparente de manière
à tracer un
tétraèdre. Il y a 2
configurations de ces 4 boules,
obtenues l'une de l'autre par la
permutation de 2 boules, images
miroir l'une de l'autre, non
superposables l'une sur l'autre. Ce
sont 2 énantiomorphes. La
boîte étant
posée sur la table, il y a 6
projections des 4 boules sur la
table, selon la face du cube
reposant sur la table, et ces 6
projections sont les mêmes
pour une configuration 3D de la
tétrade et pour son
énantiomorphe. Ces 6
projections sont les 6
configurations 2D
mentionnées.Figure
2.83.
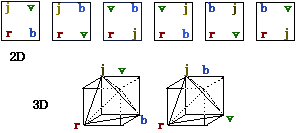
Figure 2.83. Les 6
possibilités 2D et les 2
possibilités 3D d'une
tétrade.
Nous
imaginons que les 2
représentations, 2D et 3D,
décrivent une même
réalité, celle de 4
électrons coexistant dans
l'atome du Québécium
et y formant 2 orbitales
pairées. Cette
réalité peut donc
prendre 6 aspects 2D et 2 aspects
3D. Chaque aspect 2D est en
correspondance aussi bien avec l'un
ou l'autre des aspects 3D, et
réciproquement, chaque
aspect 3D est en correspondance
aussi bien avec l'un quelconque des
6 aspects 2D. Ce que nous avons
exposé dans le chapitre qui
se termine ici repose sur des choix
raisonnés parmi ces diverses
possibilités.
Précédent
Suivant
Introduction
Chapitre
1
Chapitre 2
Chapitre
3
Chapitre
4
Chapitre
5
Chapitre
6
Courrier
QbInterna
Dernière mise à
jour : 4 novembre 2000







