4.10 Sommaire
sur les éléments
exceptionnels
Les
éléments
exceptionnels connus sont au nombre
de 19, tous d ou f. Ils
possèdent 2 numéros,
Z égal au nombre
d'électrons et Z+b
égal à Z
augmenté du nombre b des
cases lacunaires. Z+b est le
numéro descriptif, celui de
la case descriptive, où on
place l'élément pour
pouvoir lire sa formule
électronique.
Les lacunes. Les cases lacunaires
s'intercalent entre les cases de
numéros d'ordre Z et Z+b.
Elle sont au nombre de b. Elles
sont soit s soit f, jamais s et f
pour un même
élément. Si b est
supérieur à
l'unité, les cases
lacunaires sont
consécutives.
Les cases descriptives. Elles sont
exclusivement d et leur tableau est
confiné aux strates 3 et 4.
Certaines sont polyvalentes,
contenant plus d'un
élément. Leur
tableau présente une
alternance de cases monovalentes et
polyvalentes, en plus des cases
vides. Figures 4.52 à
4.54.
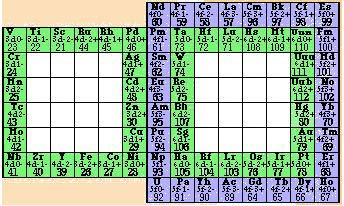
Figure 4.52.
Tableau Z 2D. Les
éléments d et f. Dans
une case : le symbole d'un
élément et la valeur
de Z.

Figure 4.53. Tableau Z+b 2D. Les
éléments d et f. Les
cases descriptives. Dans une case :
les symboles des
éléments et la valeur
de Z+b. Pour un
élément exceptionnel,
b > 0. Cases lacunaires,
monovalentes et polyvalentes. Les
cases lacunaires ne sont
descriptives pour aucun
élément.
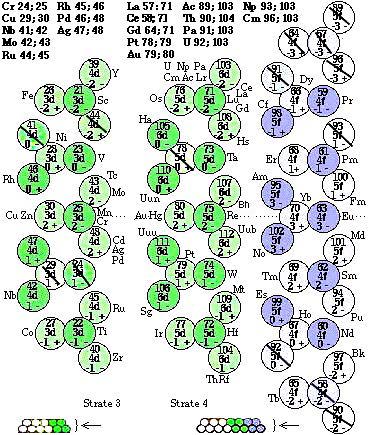
Figure 4.54.
Tableau Z+b 3D des cases
descriptives. Comme la figure
précédente mais 3D.
Formule électronique d'un
élément exceptionnel.
Elle n'est pas connue par la seule
connaissance de Z et de b. Elle est
connue par la lecture du tableau
descriptif.
Tétrades. Il apparaît
2 tétrades
d'éléments
exceptionnels au tableau Z figure
4.43 :
24, 29, 42, et 47;
57, 64, 89 et 96,
et une seule
au tableau Z+b figure 4.44 :
57, 64, 89 et 96.
Les cases polyvalentes. Les cases
71 et 103 se signalent par une
polyvalence élevée :
3 et 6. Elles se trouvent dans la
strate f et dessinent une ligne
verticale. À angle droit
avec cette ligne, les cases
polyvalentes de la strate 3
dessinent une ligne
horizontale.
Interdictions. Certaines cases du
tableau Z+b figure 4.45 sont vides.
Cela signifie qu'aucun
élément ne
possède l'une de ces valeurs
de Z+b. Ces cases sont au nombre de
12. Voici ces valeurs
interdites.
24, 29, 41, 57,
64, 78. 89, 90, 91, 92, 93,
96.
4
d'entre elles forment une
tétrade :
57, 64, 89,
96.
Cette tétrade se
fait remarquer pour la 3e
fois.
Observations. Des
régularités
apparaissent dans la
répartition des
éléments
exceptionnels.
Éléments d. Si b = 1,
la case vide et la case Z+b sont
dans la même période
et la case vide est s0+; si b = 2,
ce qui se produit pour le
palladium, il y a 2 cases s vides
dans la même période,
s0- et s0-. Il y a 2 tels
éléments
exceptionnels d dans chaque
période paire des strates 3
et 4. Il y en a 6 dans la
période impaire de la strate
3. Au total des 2 strates, il y en
a plus dans les périodes
impaires que dans les
périodes paires
Éléments
f. Présents seulement dans
la 4e strate, ils sont plus
nombreux dans la période
impaire que dans la période
paire : 5 au lieu de 2. Dans chaque
cas, b a une valeur
élevée : de 7
à 14, et les cases vides
sont f.
Ces observations indiquent
l'existence d'une
périodicité de
période égale
à la longueur d'une strate.
Figure 4. 55.

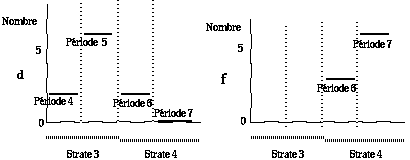

Figure 4.55.
Nombre d'éléments
exceptionnels d et f dans les
strates 3 et 4. Plus
élevé pour la
période impaire dans les
couronnes externes, soit d dans la
strate 3 et f dans la strate
4.
Et voilà une analyse des
données sur les
éléments
exceptionnels, qui pourra aider
à leur trouver une
explication théorique
satisfaisante.
4.11 Niveaux
énergétiques
La suite des cases avec leur
contenu reflète l'ordonnance
des niveaux
énergétiques des
électrons des divers
caractères. Cette suite peut
se figurer si on le désire
par un diagramme de lignes
semblable à ceux de
Grotrian, avec cependant cette
différence qu'ici les
niveaux sont occupés
simultanément chacun par un
électron.
L'établissement de lacunes
et l'apparition d'un
élément exceptionnel
à telle valeur de Z sont
liés à des
altérations de l'ordonnance
énergétique des
niveaux dans l'atome de
Québécium ayant perdu
118-Z électrons. Ces
altérations touchent Z
électrons et sont une
fonction discontinue de Z.
Exemple d'interprétation
énergétique de
l'apparition d'un
élément exceptionnel
dans le Québécium
ayant perdu 94 électrons et
en ayant conservé 24,
donnant le chrome : Cr 24;
25.
Lorsque
sont présents 24
électrons autour d'un noyau,
les électrons de
numéros d'ordre 21, 22, 23,
24 et 25 ont des niveaux
inférieurs à celui de
l'électron de numéro
d'ordre 20. Par suite, la case 20
restera vide et les 24
électrons occuperont les
niveaux 25, 24, 23, 22, 21, 19, 18
etc. Rappelons que les
numéros d'ordre
No
(identiques à Z) sont
synonymes des caractères
décrits par 4 nombres
quantiques. L'énergie d'un
électron est une fonction de
ces 4 nombres, de la valeur de Z et
de la charge du noyau
Zn.
E = E(n, l, m,
s, Z,
Zn).
E =
E(No, Z,
Zn).
On sait par l'expérience que
la charge du noyau intervient dans
cette formule par un facteur voisin
de
Zn2
sur tous les niveaux sans affecter
leur ordre. Pour l'atome neutre,
Zn = Z.
4.12 Attraction de la
sous-couche d
Tous les éléments
exceptionnels ont une
particularité en commun :
ils représentent le
remplacement d'au moins une case s
ou f dans la configuration du
Québécium par une ou
plusieurs cases d.
Réciproquement, les cases s
et f ont une particularité
commune : elles se prêtent,
à l'exclusion des cases d et
p, au remplacement par une ou
plusieurs cases d. La case
descriptive Z+b est toujours une
case d. Si certaines cases de la
sous-couche d sont
favorisées, c'est
naturellement parce qu'elles
présentent des niveaux
énergétiques
inférieurs à celles
des cases
remplacées.
Cases s remplacées. Si une
seule case s est remplacée
(b = 1), elle est s0+. Le nombre de
cases d remplaçantes va de 4
à 10. Le remplacement est
accompagné d'une diminution
de n, n devenant n-1.
Cases f remplacées. Le
nombre b de cases remplacées
va de 1 à 14. Le nombre de
cases d remplaçantes va de 1
à 2. Le remplacement est
accompagné d'une
augmentation de n, n devenant
n+1.
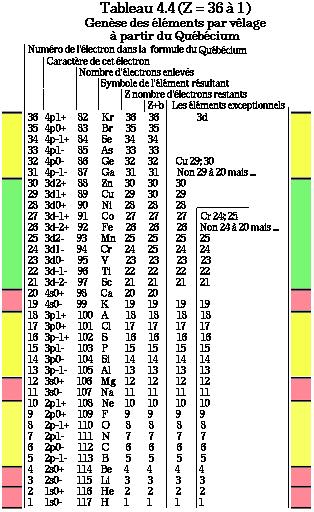
4.13 Genèse des
éléments. Tableau
d'ensemble
Dans ce qui précède,
la genèse des
éléments a fait
l'objet de descriptions 2D et 3D
recourant à la grille et au
tétraèdre du
Québécium. On
présente maintenant un
tableau de cette genèse dans
ce qui revient à un
alignement 1D, soit un tableau
ordonné par colonnes et
rangées, selon les valeurs
décroissantes de Z. Pour la
commodité de l'usager, il
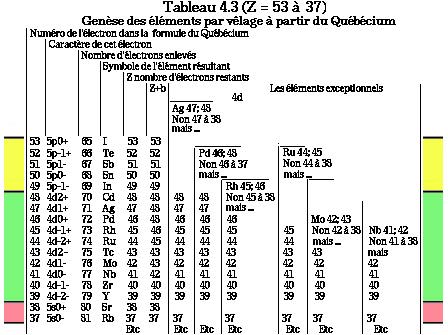
est en 4 parties. Voici son mode
d'emploi. On trouve dans la 3e
colonne le nombre
d'électrons enlevés.
Dans les colonnes voisines, on
trouve le symbole, Z et Z+b. Pour
les éléments
exceptionnels, on se reporte aux
colonnes suivantes. Etc signifie la
suite décroissante des
nombres entiers jusqu'à
l'unité.
Des ressources propres au
système du
Québécium, ce tableau
n'exploite qu'une partie, soit
celle qui touche les principes du
vêlage, qu'il met en
évidence.Tableaux 4.1
à 4.4.


4.14 Domaine
caractérisé des
éléments normaux
2D.
En examinant la figure 4.53 2D
ci-dessus, nous reconnaissons que
les 2 rangées centrales de
la grille ne renferment que des
éléments normaux. Il
y a là un domaine de 12
cases normales, en ignorant pour le
moment le problème de la
case 112. Ces cases marquent des
sous-couches
complétées ou des
demi-sous-couches
complétées.
Sous-couche complétée
ou demi sous-couche
complétée : cela
constitue une sorte de
particularité dans la suite
des configurations
électroniques des
éléments, et cette
particularité met en jeu des
nombres alternativement pairs et
impairs 5, 10, 7 et 14. Il est
satisfaisant de penser que le
respect du 2e principe du
vêlage se trouve ainsi
associé à une sorte
de régularité
physique et mathématique
dans le cas des
éléments d et
f.
Selon le principe de Hund qui
régit l'écriture de
la formule du
Québécium, les cases
de spin + d'une sous-couche se
vident consécutivement puis
celles de spin -. En termes
d'orbitales : les orbitales d'une
sous-couche se vident d'abord
consécutivement de leurs
cases de spin + et en suite de
leurs cases -. Cela suggère
qu'au cours de la genèse, il
se produit quelque chose de
particulier à la disparition
de chaque demi sous-couche. On peut
voir dans l'existence du domaine
caractérisé de cases
normales une confirmation du
principoe de Hund.
Nous avons noté
précédemment que les
cases s et p sont toujours
normales. Ainsi nous obtenons un
domaine de cases normales que nous
appelons caractérisé
à cause de sa
symétrie. Il possède
un axe de symétrie
horizontal qui est celui de la
grille du Québécium.
Il renferme 64 cases dont 2 vides
(119 et 120). Figures 4.56 et
4.57.
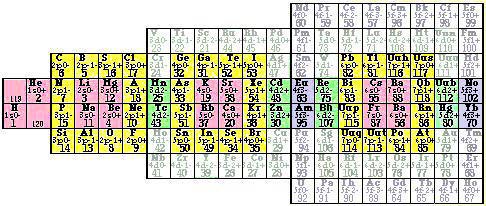
Figure 4.56. 2 D.
Domaine caractérisé
de cases normales. Noter la
symétrie par rapport
à l'axe horizontal de la
grille.
3D.
La figure 4.54 3D sur papier peut
s'analyser semblablement, les 2
rangées d et f devenant 3
tétrades alignées
selon l'axe horizontal dans la
figure. Le domaine complet 3D fait
intervenir 4 étages de
t&etrades s, 3 de tétrades
p, 2 de tétrades d et un
d'une tétrade f. Total 16
tétrades. Le tout
présente un plan de
symétrie passant par
l'arête s et perpendiculaire
à l'arête f, aussi
bien que l'ensemble du
tétraèdre. Figures
4.57 et 58.


Figures 4.57 et
4.58. 3 D. Comme la figure
précédente, mais 3 D.
10 tétrades
traversées par le plan de
symétrie et en plus 6
tétrades des sous-couches p.
Les
symétries nouvelles de ce
domaine caractérisé
ajoutent à celles
décrites plus
haut.
4.15 Tétraèdre
concrétisé du
domaine
16
tétraèdres de 4
boules chacun se prêtent
à un assemblage 3D tel que
celui montré figure
2.72.. Ici la disposition des
couleurs sera différente.
L'assemblage de boules
possède les symétries
du tétraèdre
régulier. Figure 4.59.
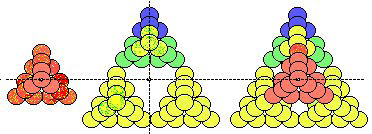
Figure 4.59.
Tétraèdre des 16
tétrades du domaine
caractérisé de cases
normales : 4 s, 9 p, 2 d et 1 f.
(64 boules). Par rapport aux boules
de chaque couleur, l'arrangement a
un plan de symétrie vertical
passant par l'arête rjb.
D'autres arrangements de
symétrie comparable sont
possibles.
Les
14 tétrades
d'éléments non
compris dans le domaine en question
peuvent s'associer en un assemblage
continu semblable à celui de
la figure ci-dessus, sauf qu'il
manque une tétrade à
chacun de 2 sommets, ce qui ne
laisse qu'une arête de 8
boules. De la sorte, l'assemblage
n'a pas les symétries du
tétraèdre
régulier, mais il a un plan
de symétrie passant par
l'arête de 8 boules et un
autre perpendiculaire au
précédent.
4.16 Prédiction :
l'élément 112 est
normal
Par extrapolation et
continuité, il est
raisonnable de prévoir que
la case 112 est normale, sinon,
elle serait la seule sur 64 en
défaut de
symétrie.
Suivant
Précédent
Introduction
Chapitre 1
Chapitre 2
Chapitre
3
Chapitre
4
Chapitre
5
Chapitre 6
CourrierQbInterna
Dernière mise à jour
: 5 novembre 2000











