Figure 5.19,
5.20.
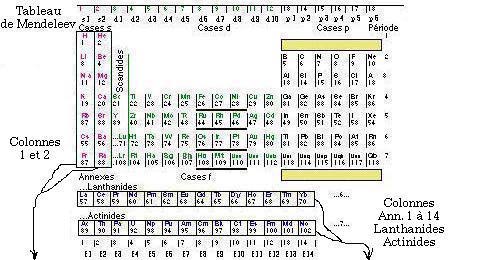
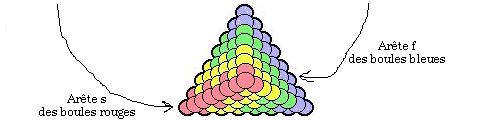
Figures 5.19,
5.20. Correspondances entre le
tableau de Mendeleev et le
tétraèdre du
Québécium. Lea
colonnes s deviennent des boules
rouges; les lignes f des
lanthanides et des actinides
deviennent des boules
bleues.
Strates
superposées. Comme il est
suggéré à la
figure
2.43, il est facile de passer
des strates alignées
à des strates
superposées. Un
modèle articulé
permet ce passage. À ce
moment, les îlots
correspondant aux colonnes du
tableau de Mendeleev se placent les
uns au dessus des autres. Figures
5.21, 5.22.
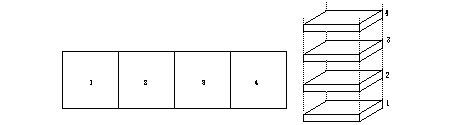

Figures 5.21,
5.22. 4 strates côte à
côte et superposées
(d'après la figure 2.43).
Modèle articulé
fermé (2D) et ouvert (3D).
Les cases vicariantes de même
couleur sont alignées
verticalement. Une broche
enfilée à travers les
strates aide à
reconnaître cet alignement.
5.8 Tableau 2D avec
diverses conventions
Le
tableau du Québécium
peut être donné avec
diverses conventions
abréviatrices concernant ce
qui apparaît dans une
case.
Le
symbole d'un élément
peut remplacer sa formule
électronique.
La formule peut
commencer par le symbole du gaz
rare de numéro
inférieur.
Elle
peut commencer par le symbole de
l'élément
complétant la sous-couche
de numéro
inférieur.
Enfin, on peut
sous-entendre les symboles et se
dispenser de les
écrire.
Exemple de la case Co 27.
Co 27
A
4s23d7
A
rermplace
1s22s22p63s23p6
Ca
3d7
Ca
remplace
1s22s22p63s23p64s2
3d7
: il y a 7 électrons
3d
Figure 5.23.
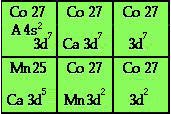
Figure 5.23.
Système du
Québécium, exemple de
la case de Co 27 avec les
conventions abrévuatrices
décrites. A, gaz rare; Ca,
sous-couche complète; Mn,
demi sous-couche
complète.
Avec
ces conventions, voyez le tableau
Figures 5.24 et 5.25.
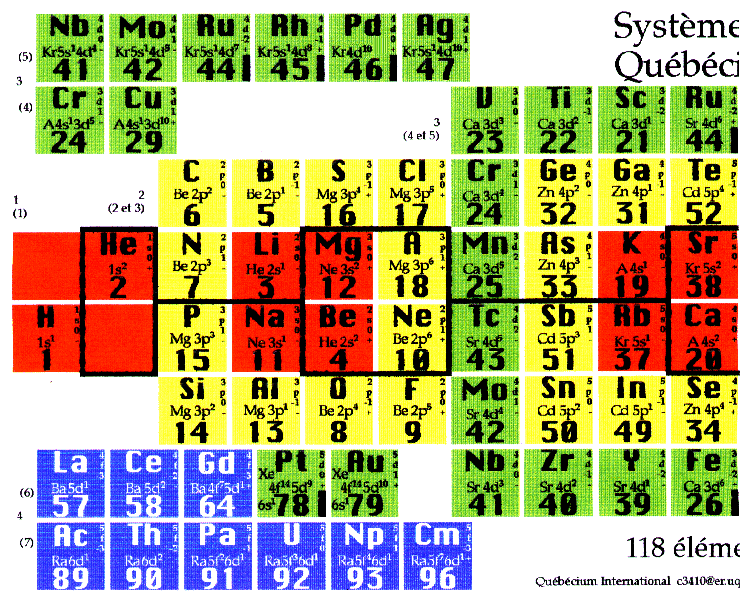

Figures 5.24 et 5.25.
Système du
Québécium, 118
éléments. Tableau 2D
avec les conventions
décrites.
5.9 Tableau 2D uniforme.
Symétries nouvelles
Dans
la version ci-dessous du tableau,
l'écriture est uniforme. De
plus, la formule de
l'élément y est
donnée avec une convention
nouvelle, ajoutasnt à la
liste ci-dessus. Au lieu des
sous-couches, on a recours aux demi
sous-couches .
La demi
sous-couche complète du
numéro inférieur est
sous-entendue.
On
se dispense d'écrire le
symbole sous-entendu.
Cette
convention est intéressante
parce que le symbole sous-entendu
est invariablement celui d'un
élément normal.
(Jusqu'à récemment,
on croyait que le technécium
Tc 43 était un
élément exceptionnel,
ce qui empêchait cette
assertion). Voici l'exemple de Co
27. Figure 5.23.
Co 27
3d2
Le symbole
sous-entendu est Mn 25, de
formule
1s22s22p63s23p64s23d5
3d2
: il y a 2 électrons
3d.
Symétrie
et tétrades. Cette
convention fait apparaît
entre les cases une symétrie
nouvelle concernant les formules
affichées sauf les valeurs
de n. À l'intérieur
d'une strate, il y a une
symétrie miroir des cases
entre le haut et le bas, la gauche
et la droite; un axe de
symétrie vertical et un
autre horizontal; un axe de
rotation binaire perpendiculaire
aux 2 autres. Chaque case
appartient à une
tétrade facilement
repérable dans la nouvelle
convention d'écriture, parce
que ses 4 cases affichent la
même formule sauf n. Figure
5.26.
Exemple la
tétrade du cobalt. Voyez les
4 cases
3d2,
4d2.
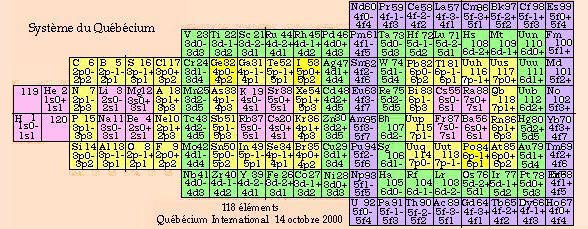
Figure 5.26.
Système du
Québécium. 118
éléments. Tableau 2D
uniforme avec une convention
nouvelle dans l'écriture de
la formule, le symbole
correspondant à une demi
sous-couche étant
sous-entendu. Les formules se
répondent sauf les valeurs
de n entre le haut et le bas, la
gauche et la droite dans chaque
strate. Exemple
3d2 et
4d2.
Une
figure met en évidence les
cases demi sous-couches. Figure
5.27.

Figure 5.27. Les
38 demi sous-couches.
5.10
Un retour à
l'équerre
La
dernière figure
suggère une nouvelle
unité dans la classification
des éléments : c'est
l'équerre, comprenant 1, 3,
5 ou 7 cases, discutée plus
haut dans l'analyse de la formule
du Québécium.Voyez 2.3.3.1.Représentations
bidimensionnelles.
L'équerre apparaît
comme l'unité naturelle par
excellence de la
classification.
Équerre
2D dans la strate 3. La figure 5.28
montre un exemple d'une
équerre faisant suite
à une demi
sous-couche.

Figure 5.28. Une
équerre 2D faisant suite
à la demi sous-couche Ca 20
dans la strate 3.
Il
y a autant d'équerres qu'il
y a de demi sous-couches
complètes. On compte ainsi
38 demi sous-couches et 37 ou 38
équerres
d'éléments. C'est une
question de définition de
choisir entre 37 et 38, selon qu'on
considère la case H 1,
équerre d'une case, comme
constituant une équerre
admissible. Elle ne suit aucune
demi-sous-couche
complète.
L'équerre
et la demi sous-couche s'ajoutent
aux unités naturelles de
classification des
éléments,
après la période, la
strate, la couche et la
sous-couche. On connaît par
ailleurs la colonne, le groupe et
la famille.
Équerres
en 3D. 4e strate. Dans les
représentations 3D. les
équerres 2D deviennent des
équerres 3D qui sont en
réalité rectilignes,
des enfilades de boules. Voici les
équerres 3D de 7 cases des
demi sous-couches f dans la 4e
strate. Figure 5.29. 
Figure 5.29.
Équerres 3D des demi
sous-couches complètes f de
la 4e strate, qui sont des
équerres
géométriques en 2D.
Ici, les équerres 3D sont
des enfilades complètes de
boules, une dans chacune des 7
tétrades de boules. Il y a
là une apparence de
solidité structurale pour la
structure
tétraèdrique, allant
de pair avec la
régularité de la
configuration électronique.
D'après figure 2.64.
5.11 L'équilibre du
tétraèdre
concrétisé et l'ordre
pdfs
Des
considérations sur
l'équilibre du
tétraèdre du
Québécium
modifié par soustraction de
boules conduisent à
justifier la règle sur
l'ordre d'apparition des
éléments, sfdp par
synthèse ou pdfs par
genèse.
Ordre
pdfs. Nous partons du
tétraèdre complet
reposant sur la table par son
étage 1, le contact
étant de 36 boules. Son
polygone de sustentation est un
triangle équilatéral
ayant 8 boules de
côté.
Voici
l'exemple, particulièrement
démonstratif, de l'europium
Eu 63 obtenu par suppression de 55
boules. Le polygone est un triangle
que 8 boules dessinent, soit une
boule 6s (56) (de numéro 56)
de l'étage 1 et 7 boules 4f
(57 à 63) de l'étage
2. Il n'y a pas de porte à
faux, mais le
tétraèdre
modifié est penché,
d'environ
7o. Le
contact avec la table est de 8
boules. Figure 5.30. 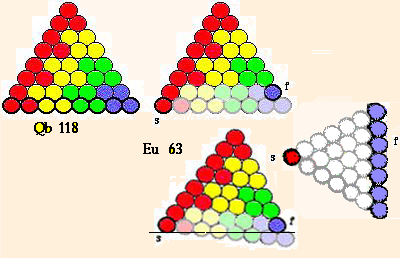
Figure 5.30. Le
polygone de sustentation de
l'europium Eu 63 : un triangle
défini par la boule 56 et
l'enfilade de boules 57 à
63. L'inclinaison préserve
le plan de symétrie passant
par l'arête des boules
rouges.
On
pourrait faire des observations
comparables sur le manganèse
Mn 25 et sur l'azote N 7
etc.
Le
polygone de sustentation du carbone
C 6, obtenu par suppression de 112
électrons, est un triangle
isocèle ayant les boules 5
et 6 aux sommets semblables et la
boule 4 à son autre
sommet.
Si
la genèse procédait
dans un ordre autre que pdfs, cela
favoriserait l'apparition
d'empattements moins larges et de
porte-à-faux plus
importants.
Atomes
exceptionnels. Des
considérations semblables
pourraient aider à
comprendre la raison des atomes
exceptionnels.
Précédent
Suivant
Introduction
Chapitre 1
Chapitre 2
Chapitre
3
Chapitre
4
Chapitre
5
CourrierQbInterna
Dernière mise à
jour : 5 novembre 2000











