QbSyst2e.16.html
Système du Québécium
Suivant QbSyst2e.18.html
Précédent
QbSyst2e.16.htmlDébut QbSyst2e.1.html
Chapitre 9
Applications aux éléments
Placements des électrons dans la formule du québécium
Les orbitales

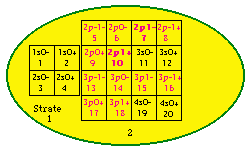
Fig. 198. Strates 1 et 2. Les cases renferment les électrons de 1 à 20 de la formule du québécium. Les électrons p sont mis en évidence et parmi eux, ceux d'une orbitale doublement. Les numéros sont les numéros électroniques.
Symétrie et orbitales.Pourquoi placer des électrons (ou plutôt leurs caractères) d'une manière ou d'une autre dans une grille? Futilité, caprice, exercice vain?
Je propose au lecteur que la question du placement des électrons dans la formule du québécium est un jeu d'ordonnance et de symétrie et que ce jeu peut être passionnant et nous révéler des propriétés importantes de la matière inerte.
Le concept d'orbitale aura un rôle clé pour jouer ce jeu.
Ce concept a conduit à expliquer les liaisons covalentes en chimie. Voyez par exemple Gressier.
http://www.univ-lemans.fr/enseignements/chimie/02/gressier/liaisons.pdf
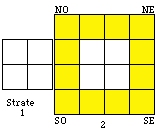
Fig. 199. Strates 1 et 2. Couronne des électrons p, couronne p.
Les orbitales dans la formule du québécium.
Si le lecteur décompte avec moi les signes + et - du tableau figure 197, désignant la valeur du spin s, il reconnaîtra facilement qu'ils sont présents en nombres égaux. Voyez la légende figure 195 et l'Annexe A. Toutes les orbitales sont complètes.
De plus, il reconnaîtra ensuite que les caractères des électrons se présentent par paires, identiques au dernier signe près. Exemple les termes 5 et 8.
2p1-
........2p1+Une telle paire forme une orbitale. On dit encore que l'un des termes est l'orbitale de l'autre : 2p1- est l'orbitale de 2p1+ et réciproquement; ou encore que chaque terme est ou possède une orbitale.
Les cases 1 à 20. Restreignons notre examen aux 20 1res cases, constituant les strates 1 et 2. Nous y découvrons 10 orbitales : 4 sont s, 6 sont p. Figure 198.
Nous convenons de garder intacte la grille et son contenu, mais de réarranger ce contenu dans un nouveau placement qui serait plus esthétique et plus symétrique. Nous convenons aussi de garder intact le contenu d'une strate. Une idée de placement serait évidemment de placer côte à côte les cases orbitales. Une autre serait de les unir 2 en une seule, alors nous aurions 10 cases au lieu de 20 avec une économie d'espace occupé. Mais ce serait dommage, car mieux vaut préserver l'identitification de chaque électron à une case plutôt que la sacrifier pour un bénéfice qui n'est pas évident.
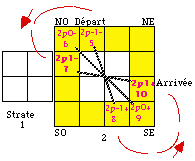
Fig. 200. Placement de 3 orbitales dans la couronne p. Les pointillés marquent les 3 orbitales.
Des orbitales centrées. Nous proposons plutôt d'affirmer la symétie binaire des orbitales, en plaçant les 2 cases de chaque orbitale symétriquement par rapport au centre de figure de la strate. Ainsi 2p1- et 2p1+ devraient apparaître symétriquement par rapport au centre de la strate 2. Cela peut se faire de 8 façons. De même l'orbitale 2p-1- et 2p-1+, etc.
Les cases p. Restreignons encore le domaine de notre examen, aux seuls électrons p, lesquels sont au nombre de 12.
Nous voyons immédiatement qu'ils sont disponibles pour réaliser une couronne centrée sur le centre de la strate 2, couronne de 12 cases précisément. Figure 199.
La couronne des cases p. Quelle heureuse trouvaille! Nous avons trouvé une manière heureuse - lisez symétrique, de placer nos 12 électrons p! Nous les plaçons donc dans les 12 cases de la couronne décrite.
Mais notre travail n'est pas teminé : ces électrons ne sont pas interchangeables. Ils présentent 12! permutations
Nous avons toute raison de préserver les ordonnances diponibles, celles des numéros électroniques, que voici.
5, 6, 7, 8, 9, 10; 13, 14, 15, 16, 17, 18.
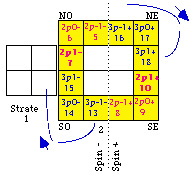
Fig. 201. Placement de 3 autres orbitales dans la strate 2, numéros électroniques 13 à 18
Les premiers rencontrés auront priorité, soit 5, 6, 7. Nous les garderons côte à côte. Par suite du principe ci-haut, ils déterminent la place de leurs orbitales 8, 9, 10, que voici.
8 en regard de 5, 9 en regard de 6, 10 en regard de 7.
Les électrons 5, 6, 7... Pour placer les électrons 5, 6, 7 côte à côte et symétriquement dans la couronne, il est nécessaire de les disposer en équerre de 3 dans l'un des 4 coins.
Les équerres. Nous convenons que la progression numérique des numéros électroniques, comme celle des strates, aboutira à l'est. Nous convenons aussi que le départ est au nord. Alors il faut choisir un départ vers la gauche, par le coin NO et vers le bas. La lecture des numéros électroniques consécutifs est une rotation senestre, dans le sens invere des aiguilles d'une montre. Cela détermine l'occupation de 6 des 12 cases de la couronne tel que dessiné dans la Figure 200.
Le résultat est une paire d'équerres opposées, ayant chacune 3 cases et l'occupation de 6 cases sur 12. Figure 200
Des pointillés unissent les cases des orbitales.
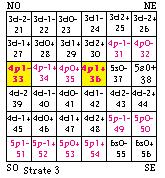
Fig. 202. Strate 3 de la formule du québécium. Les électrons p sont mis en évidence et parmi eux, ceux d'une orbitale doublement. Les numéros sont les numéros électroniques.
Les électrons 13, 14, 15... Pour continuer notre ouvrage, nous avons plusieurs choix, entre autres 2 coins sont disponibles. Le sens de rotation sera choisi dextre par symétrie du précédent. Le départ est choisi pour que la case 18 aille avoisiner la case 10, ainsi les numéros les plus élevés se jouxtent à l'ouest. Le départ est au sud. Figure 201.
Le quantum principal. Notons la répartition de n, quantum principal. Il vaut 2 dans les équerres NO et SE, et 3 dans les équerres SO et NE.
Le spin. La répartition du spin est plus simple : - dans le demiant O, + dans le demiant E.
Conclusion pour les strates 1 et 2. Nous avons réussi à manifester une organisation remarquablement symétrique inhérente aux électrons p de la formule du québécium dans les strates 1 et 2 : ils se disposent naturellement en une couronne de 12 cases où il est immédiat de reconnaître 6 orbitales.
Nous avons mis de côté les électrons s.

Fig. 203. Strate 4 de la formule du québécium. Les électrons p sont mis en évidence et parmi eux, ceux d'une orbitale doublement. Les numéros sont les numéros électroniques.
Strates 3 et 4. Les couronnes p de la formule du québécium
.Les strates 3 et 4 renferment l'une et l'autre 12 électrons p, les cases étant comme suit. Figures 202, 203.
Strate 3 : 31, 32, 33, 34, 35, 36; 49, 50, 51, 52, 53, 54.
Strate 4 : 81, 82, 83, 84, 85, 86; 113, 114, 115, 116, 117, 118.
Nous pouvons naturellement en former 2 nouvelles couronnes p, semblables à celle de la strate 2 sauf les quanta principaux : 4 et 5 dans la strate 3, 6 et 7 dans la strate 4. Les 3 couronnes p disponibles dans la formule du québécium sont visibles dans la figure 204.
Le quantum principal. Notons la répartition de n, quantum principal. Il vaut 4 ou 6 dans les équerres NO et SE, 5 ou 7 dans les équerres SO et NE.
Le spin. La répartition du spin est plus simple : - dans le demiant O, + dans le demiant E de chaque strate.

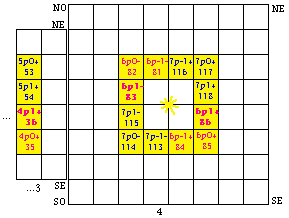
Fig. 204. Les 3 couronnes p de la formule du québécium. Les 6 orbitales de chaque strate sont marqueés par une étoile à 6 branches.

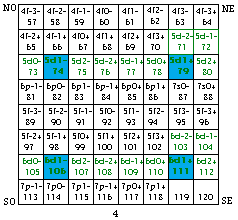
Fig. 205. Strates 3 et 4 de la formule du québécium. Mise en évidence des cases d et parmi elles doublement, de celles de 4 orbitales
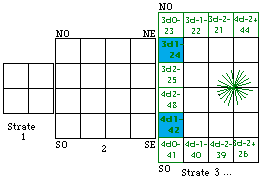
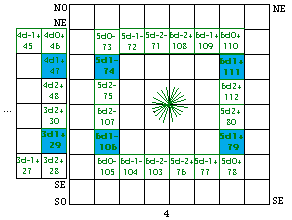
Fig. 206. Les 2 couronnes d de la formule du québécium. Les 10 orbitales d de chaque couronne sont marquées par une étoile à 20 branches.
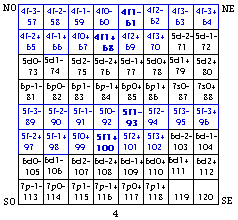
Fig. 207. Strate 4 de la formule du québécium. Mise en évidence des cases f et parmi elles doublement, de celles de 2 orbitales
Les couronnes d de la formule du québécum.
Ce que nous avons reconnu et fait pour les électrons p de la formule du québécium, nous pouvons facilement le répéter pour les électrons d, mutatis mutandis. Absents des strates 1 et 2, ils sont présents dans les strates 3 et 4. La figure 205 les met en évidence.
Leurs cases sont donc mises en équerres puis assemblées en couronnes dans la figure 206.
Les équerres d ont 5 cases, les couronnes d ont 20 cases.
Seulement 2 couronnes d, alors qu'il y a 3 couronnes p. Une étoile à 10 branches marque les orbitales dans chaque couronne d.
Le quantum principal. Notons la répartition de n, quantum principal. Il vaut 3 ou 5 dans les équerres NO et SE, 4 ou 6 dans les équerres SO et NE.
Le spin. La répartition du spin est plus simple : - dans le demiant O, + dans le demiant E.
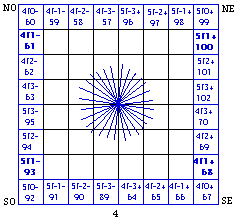
Fig. 208. L'unique couronne f de la formule du québécium. Les 14 orbitales f de cette couronne sont marquées par une étoile à 28 branches.
Les couronnes f de la formule du québécum.
Ce que nous avons reconnu et fait pour les électrons d et p de la formule du québécium, nous pouvons facilement le répéter pour les électrons f, mutatis mutandis. On ne trouve d'électrons f que dans la strate 4. Ils sont mis en évidence puis en équerres et en couronne aux figures 207 et 208.
Les équerres f ont 7 cases, la couronne f a 28 cases.
Seulement 1 couronne f, alors qu'il y a 2 couronnes d et 3 couronnes p.
Une étoile à 28 branches marque les 14 orbitales de cette couronne f.
Le quantum principal. Notons la répartition de n, quantum principal. Il vaut 4 dans les équerres NO et SE, 5 dans les équerres SO et NE.
Le spin. La répartition du spin est plus simple : - dans le demiant O, + dans le demiant E.
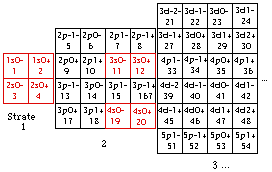
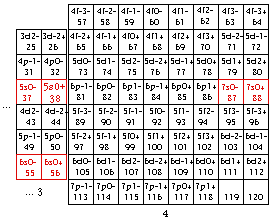
Fig. 209. La formule du québécium avec mise en évidence des cases s.
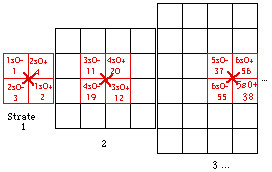
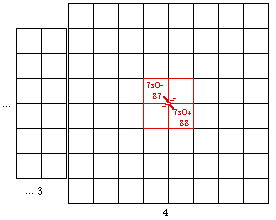
Fig. 210. Les 4 couronnes s de la formule du québécium. Une étoile à 4 branches marque les orbitales.
Les "couronnes" s de la formule du québécium.
Laissées de côté, des cases s sont présentes dans les 4 strates de la formule du québécium, chaque fois sous la forme d'orbitales complètes de 2 cases. Ce que nous avons reconnu et fait pour les électrons d et p de la formule du québécium, pouvons-nous le répéter pour les électrons s?
La question se pose puisque la création d'une équerre proprement dite et d'une autre équerre en regard requiert au minimum 2 fois 3 cases, évidemment introuvables dans une orbitale de 2 cases.
Qu'à cela ne tienne! Nous allons convenir, afin d'uniformiser le langage,
d'étendre la notion d'équerre dans un tableau de manière à inclure la case isolée. Nous avons déjà proposé telle extrapolation : une équerre d'une case est une équerre de bras nuls, b = 0, v = 1 aux figures 6 et 8. Deux cases côte à côte n'ont pas la symétrie d'une équerre. Une case isolée si.
Par extrapolation de langage encore, nous conviendrons d'appeler couronne un assemblage de 4 équerres b = 0, quoiqu'il n'encadre aucun espace vide; disons qu'il entoure un espace nul, égal à 0. Il l'entoure symétriquement. Figure 11.
Nous procédons donc à repérer les cases s à l'intérieur de chacune des strates. Figure 209.
Puis nous essayons de les assembler en couronnes de 4 équerres d'une case, les orbitales traçant une diagonale. Figure 210.
Nous trouvons 3 couronnes complètes, une dans chacune des strates 1, 2 et 3, et une demi-couronne de 2 cases seulement dans la strate 4. Au total 4 couronnes dont une incomplète, 7 orbitales et 14 cases. Une étoile à 4 branches marque les orbitales dans chaque couronne et demi-couronne.
Formule du québécium en couronnes et orbitales.
Nous possédons maintenant une collection de couronnes couvrant toutes les strates et toutes les orbitales de la formule du québécium. Le temps est venu de les réunir. Les couronnes s, p, d et f s'emboîtent pour donner un assemblage compact s'étendant du numéro 1 au numéro 118. Dans chaque strate elles déterminent es qudrants grilles carrées.
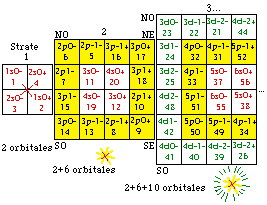
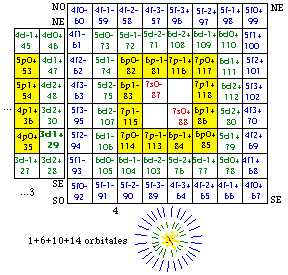
Fig. 211. Formule du québécium en couronnes.
C'est là une version de la formule du québécium ordonnée selon les critères de symétrisation décrits ci-haut en 1er lieu pour les électrons p. Voici cette formule, appelons-la en couronnes, nous pourrions l'appeler en orbitales. Figure 211. Les étoiles emboîtées marquent les orbitales; les nombres d'orbitales par strate sont indiqués.
Une remarque se présente du premier coup d'oeil : 2 cases sont vides au delà de la 118e. Il est tout indiqué de les remplir par les caractères de 2 électrons spéculatifs 8s0- et 8s0+. Cela correspond à un atome de québécium ionisé 1 ou 2 fois négativement, oïde de 2 atomes spéculatufs, l'alcalin Z = 119 ou de l'alcalino-terreux Z = 120.
Rappelons que, selon certains théoriciens, une vallée spéculative de stabilité existerait au voisinage de Z = 120, par parallélisme avec celle connue expérimentalement et décrite dans le modèle de Goeppert-Mayer pour les neutrons du noyau au nombre de 120. Il existerait ainsi une toute petite probabilité que l'élément 120 soit un jour réalisé.
La formule du québécium 120 cases est présentée à la figure 212. Qu'elle arrête à la case 118 ou à la case ne change pas la qualité du québécium d'être le gaz rare spéculatif terminant la 7e période mendélévienne des éléments. L'intérêt de montrer 120 cases est de nature esthétique, il réside dans la symétrie accrue qui apparaît ainsi. Autrement, le tableau paraît incomplet.
Nous allons maintenant raisonner sur la base de la formule du québécium ayant 120 cases occupées. Formule 120 cases, figure 212.
Propriétés de la formule du québécium en couronnes.
Faisons le bilan de la formule du québécium à laquelle nous avons abouti. Tableau 55.

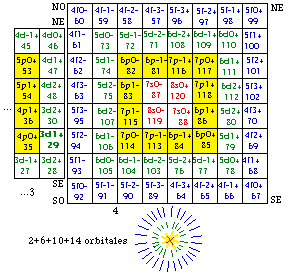
Fig. 212. Formule du québécium en couronnes 120 cases.
Tableau 56. Bilan de la formule du québécium.
120 cases
120 caractères de 1s0- à 8s0+
60 orbitales de 1s0 à 8s0
10 couronnes dont 4 s, 3 p, 2d et 1 f
ayant respectivement 4, 12, 20 et 28 cases chacune
40 équerres dont 16 s, 12 p, 8 d et 4 f
Il apparaît que cette formule répond à des degrés d'organisation qui sont les suivants. Tableau 56.
Tableau 567. Niveaux d'organisation de la formule du québécium.
case = caractère d'un électron
équerre = demi sous-couche spins de signe unique
double équerre de quadrants en regard = sous-couche valeur unique de l quantum azimual
couronne = même valeur de l quantum azimutal au signe près
strate = couronnes emboîtées croissance centripète de n quantum principal;
demiant O = spin -
demiant E = spin +
quadrants = les quadrants en regard ont la même organisation des valeurs de n
formule = n quantum principal central croît de l'0uest vers l'est, 1, 3, 5, 7 double équerre NO SE, 2, 4, 6, 8, double équerre SO NE
Le niveau le plus fondamental est celui des équerres renfemant des demi sous-couches.
De nombreuses symétries existent dans la fomule figure 212. On en montre l'esentiel dans la figure 213, où seules les cases diagonales des strates apparaissent.
Demi sous-couches, quantum magnétique et "nombres carrés".
Chaque équerre renferme une demi sous-couche où le nombre de caractères permis est 2l+1, soit l'un des nombres impairs 1, 3, 5, 7. Les sommes possibles de ces nombres sont 1, 4, 8 et 16, soit les carrés des nombres entiers. Les équerres emboîtées ne peuvent pas manquer de dessiner des carrés.
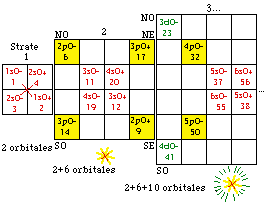
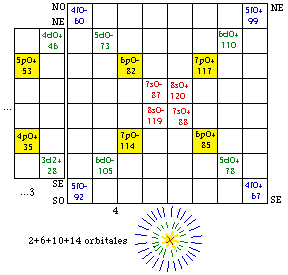
Fig. 213. Formule du québécium 120 cases, seules cases diagonales.
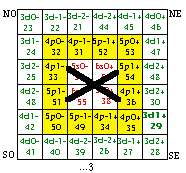
Fig. 214. Une tétrade p1 dans la strate 3.
Nous rencontrons ici les "nombres carrés" évoqués au chapitre 1. La théorie de Schrödinger, dans sa partie qui s'applique aux électrons de tous les atomes, a une affinité avec la théorie des nombres carrés.
Symétries d'ordre 4. Tétrades d'électrons.
La formule figure 212 présente une symétrie d'ordre 4 dans chacune de ses strates. Deux cases de quadrants opposés par rapport au centre de figure forment une orbitale. Mais chaque paire de cases ainsi déterminée a son symétrique par rapport à l'axe NS ou OE, soit une 2e orbitale. Toutes les cases appartiennent ainsi à des paires d'orbitales vicariantes.
Les 120 cases de la formule forment naturellement 30 telles paires d'orbitales. Nous les appellerons des tétrades.
Voici l'exemple des électrons d'une tétrade dans la strate 3. Figure 214.
4p1-, 4p1+, 5p1-, 5p1+
Tous ces électrons sont p1. Ils ont même valeur du quantum azimutal l = 1 et du quantum magnétique m = 1. Leurs spins et leurs quanta principaux diffèrent d'une unité.

Fig. 215. Un tétraèdre régulier.
Forces électromagnétiques de symétrie tétraédrique.
Entre eux existe l'affinité géométrique décrite. Il faut croire qu'il existe aussi une affinité physique. Cette affinité physique se conçoit comme une tendance des électrons p1 à former un groupe de 4. La seule disposition plausible dans l'espace a nécessairemnent les symétries d'un tétraèdre régulier. On imagine que les vecteurs associés aux spins sont orientés selon les normales aux 4 faces d'un tétraèdre régulier. Figure 215.
Les forces électromagnétiques correspondantes expliqueraient les désaccords entre la formule connue du québécium et celle prévue par la théorie normale.
Le principe de Pauli, lié aux forces de symétrie 2 entre électrons de spins - et +, explique les paires de cases formant une orbitale. L'existence de tétrades, qui sont des doubles orbitales, réclame des forces de symétrie 4.
Ces forces devraient avoir une relation avec les propriétés magnétiques des éléments.
Tétravalence du carbone.
Il faut signaler l'analogie entre les forces ci-dessus et celles qui assurent la tétravalence du carbone dont la formule à 6 électrons ne présente pourtant pas 4 électrons semblables.
(2 électrons n = 1) 2s0-
...2s0+...2p-1-...2p0-Or il est bien connu que les 4 valences du carbone sont indiscernables, par exemple dans le méthane CH4. Il faut admettre par conséquent que les paires d'électrons 2s et 2p ont un même comportement quoiqu'elles forment des orbitales différentes. Voici comment Gressier s'exprime à leur sujet.
"
Les 4 électrons périphériques du C par exemple ont donc la même nature, intermédiaire entre le s et le p, du fait des échanges permanents. Par voie de conséquence les 4 orbitales s et p se dégénèrent ou s’hybrident pour donner 4 orbitales hybrides nommées sp et dont les caractéristiques sont intermédiaires entre les orbitales s pure et p pure".Utilisant le langage de cet auteur : les électrons des tétrades ci-haut ont même nature.
Le cas du carbone, qui a l'avantage sur tout autre atome pour assurer la vie, mérite notre attention. Cet avantage est lié à la souplesse de ses liaisons, elles mêmes dépendant évidemment des particularités de sa tétravalence. Cette tétravalence a des ressemblances avec l'organisation des électrons en tétrades dans chaque strate.
L'atome de carbone est minuscule. Il est fait surtout de 4 électrons de valence, avec un oïde de l'hélium au centre.
Une logique de symétrie.
Pourquoi la formule du québécium est-elle ce qu'elle est et non pas celle prévue par la théorie normale? C'est parce qu'il est nécessaire qu'elle réalise les symétries inhérentes au système du québécium que nous venons de reconnaître.
Ces symétries se ramènent à un agencement d'équerres ayant chacune une valeur de l imposée :
l = 0, 1 case
........l = 1, 3 cases ........ l = 2, 5 cases........ l = 3, 7 cases
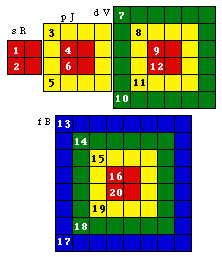
Fig. 216. Lieux d'insertion des sous-couches. Le numéro s'attache aux 2 équerres opposées. Quantum azimutal l : code coloré.
Une logique de symétrie.
Pourquoi la formule du québécium est-elle ce qu'elle est et non pas celle prévue par la théorie normale? C'est parce que des exigences naturelles, exprimées par le système du québécium, lui imposent la réalisation de certaines symétries.
Ces symétries se ramènent à un agencement de couronnes ayant chacune une valeur du quantum azimutal l imposée par le nombre de cases que les orbitales doivent remplir.
Le recrutement des sous-couches.
Voici le nombre de sous-couches qu'il nous faut pour remplir les 4 strates.Tableau 58.
Tableau 58. Les sous-couches nécessaires.
8 sous-couches s, l = 0
6 sous-couches p, l =1
4 sous-couches d, l = 2
2 sous-couches f, l = 3
Nous convenons de les recruter dans les couches de nombres quantiques principaux n les plus petits, dans l'ordre. Pour cela, nous consultons le Tableau 55 donnant les valeurs permises de l pour chaque couche. En voici un abrégé annoté. Tableau 59.
Tableau 59. Recrutement des sous-couches.
Lieu d'insertion figure 216.
n
........l ........Lieu1
........0 ........12
........0 ........22
........1 ........33
........0 ........43
........1 ........53
........2 ........74
........0 ........64
........1 ........84
........2 ........104
........3 ........135
........0 ........95
........1 ........115
........2 ........145
........3 ........175
........4 .........6
........0 ........126
........1 ........156
........2 ........186
........3 .........6
........4 .........6
........5 .........7
........0 ........167
........1 ........197
........2 .........7
........3 .........7
........4 .........7
........5 .........7
........6 .........8
........0 ........208
........1 .........Etc
Le résultat correct s'ensuit.
La formule du
québécium
réclame le système du
québécium.
Nous pouvons raisonner à l'inverse : la formule du québécium ne peut se comprendre qu'en faisant appel au système du québécium. Elle en démontre le bien-fondé.
![]()
QbSyst2e.16.html
Système du Québécium
Suivant QbSyst2e.18.html
Précédent
QbSyst2e.16.htmlDébut QbSyst2e.1.html