QbSyst2e.3.html

Suivant QbSyst2e.4.html

Chapitre 1

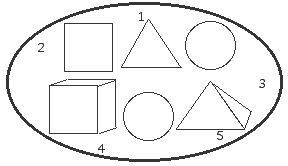
Fig. 1. Quelques nombres entiers, quelques figures à 2 et à 3 dimensions qui sont à la base du système du québécium.

"Les nombres carrés", cela signifie la suite indéfinie des entiers impairs positifs. Leur somme, arrêtée à un nombre arbitraire de la suite, est égale au carré d'un entier. Les sommes successives donnent les carrés des entiers successifs. Tableau 1.

1 = 1 = 1²

1+3 = 4 = 2²

1+3 +5 = 9 = 32

1+3 +5+7 = 16 = 4²

1+3+5+7+9 = 25 = 5²

1+3+5+7+9+11 = 36 = 6²

1+3+5+7+9+11+13 = 49= 7²

etc

Le nombre porté au carré est égal au nombre de termes.

Fig. 2. Mots croisés. Exemple d'un tableau de 144 cases.

Cette propriété curieuse des nombres est introuvable dans les traités d'arithmétique. L'auteur en a appris l'existence dans l'encyclopédie thématique Weber datée de 1969, dans un article, probablement de François Le Lionnais. Elle est importante pour ce qui suit.

Qui n'a pas un tableau chez lui, accroché au mur? Telle est bien la notion la plus courante d'un tableau : un objet d'art, avec son cadre, le plus souvent le tout bidimensionnel et de forme rectangulaire. Au point de vue mathématique, nous conviendrons qu'un tel tableau ne contient qu'un objet, l'objet d'art lui-même.

Toute salle de classe digne de ce nom possède un tableau (noir ou vert), où des objets tracés à la craie ou au feutre ont une existence éphémère et plus ou moins organisée.

Les tableaux d'affichage sont plus près de nos intérêts. Dans les babillards, il s'épingle des objets ayant chacun son individualité. Puis il y a, dans la vie courante, les tableaux des départs et arrivées dans les gares et aérogares et les horaires de toutes sortes qui sont aussi des tableaux. Mais les exemples les plus caractérisés sont les mots croisés, le damier, l'échiquier et les autres surfaces divisées servant à des jeux de société. Figure 2.

Fig. 3. La rose des vents d'un tableau.

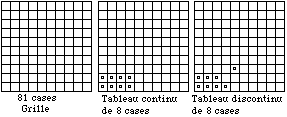
Fig. 4. Grille, tableau continu, tableau discontinu.

Dans la vie scientifique, il y a les tables de constantes à double entrée, etc.

Un peu comme monsieur Jourdain qui faisait de la prose sans le savoir, monsieur Tout le monde se sert de tableaux sans trop se soucier de les définir. Les matrices, définies depuis longtemps, renferment des nombres ou des quantités destinées à réaliser des opérations selon les règles de l'algèbre linéaire. Mais tout tableau n'est pas nécessairement une matrice et la notion de tableau, entité mathématique composé de cases, est d'apparition récente. Voici une tentative de formalisation.

Tableau. 1. Espace bidimensionnel où l'on peut reconnaître des rangées horizontales et des colonnes verticales. Il faut pour cela que la surface contienne la verticale, sinon, il faut dire : des colonnes à angle droit avec les rangées. Cet espace peut s'étendre indéfiniment ou être limité, par exemple à un carré contenant autant de rangées que de colonnes. S'il a 8 cases de côté, on dira un tableau 8X8.

Le tableau est un moyen fondamental d'occuper et d'organiser l'espace.

Un tableau est orienté de sorte qu'on peut y reconnaître les points cardinaux de la rose des vents, le nord en haut. 2. Ensemble des cases occupées par des objets d'un tableau 1. Figure 3.

Tableau continu. Tableau 2 dont chaque case a un côté en commun avec une autre Figure 4.

Tableau discontinu. Tableau 2 dont une case au moins n'a aucun côté en commun avec une autre.

Case. L'une des portions constitutives d'un tableau définie par une rangée et une colonne. Les cases peuvent être vides ou occupées par des objet. Pour simplifier, on les suppose toutes égales et de forme carrée.

Objet. Ce qu'on place dans une case, objet réel ou symbolique. Règle générale, un tableau est destiné à recevoir des objets, à priori de forme et de dimension quelconques L'objet peut être un tableau contenant à son tour des objets.

Tableau vide. Tableau 1. On dira de préférence grille. Même vides, ses cases peuvent avoir une signification comme domaine accessible à des objets.

Tableau occupé. Tableau 1 modifié par la présence d'au moins une case occupée.

Grille. 1. Tableau vide. 2. En mots croisés : tableau vide sauf certaines cases inaccessibles.

Quantification. Un tableau donne l'exemple d'une quantification spatiale et conceptuelle. Par hypothèse, un objet du tableau se trouve dans une case ou une autre, son placement est discret, il n'y a pas de placement intermédiaire entre deux cases. En passant d'une case à l'autre, on passe d'un objet à un autre. Il n'y a qu'un objet par case.

Tableaux et repères. Un tableau et un repère de coordonnées en x et y ont beaucoup en commun : ils concernent le placement d'un objet. La différence réside dans une quantification du placement de l'objet supposé ponctuel. À l'intérieur d'une case d'un tableau, la position exacte d'un point est indifférente, étant définie par deux numéros d'ordre, ceux de la colonne et de la rangée respectivement. Il en est autrement des coordonnées x et y de ce point.

Placement. Le choix d'une case ou d'une autre pour un objet ou chacun de plusieurs objets. Au besoin, la position d'un objet sera prise comme étant le point central de la case.

Les jeux de société. De nombreux jeux de société se jouent sur des tableaux tels que le damier et l'échiquier. Ils donnent lieu à des développements mathématiques considérables, où intervient la dynamique des placements et déplacements. Le damier et l'échiquier sont des grilles, tableaux vides. Le damier a 10 rangées et 10 colonnes soit 100 cases; l'échiquier a 8 rangées et 8 colonnes soit 64 cases. Une fois les pièces en place, ils sont des tableaux occupés.

L'écriture offre un exemple remarquable d'un tableau d'une rangée et d'un nombre indéfini de colonnes. Chaque case contient un caractère, selon les règles de la grammaire. Ce tableau idéal serait très encombrant et pour cette raison on recourt à l'alinéa après un certain nombre de cases occupant une rangée.

Un dictionnaire offre l'exemple d'un tableau où chaque case renferme à son tour un tableau, celui de l'écriture d'une entrée.

Combinatoire. Nombre de combinaisons. Étant donné une grille de n cases, son occupation par des objets tous semblables donne lieu à un grand nombre de combinaisons possibles, selon les placements des objets.

1 objet : n combinaisons

2 objets : n(n-1)/2 combinaisons

etc

Certaines de ces combinaisons peuvent être congrues avec d'autres. Le problème de placer des objets dissemblables est vaste.

Congruence. 1. À 2 dimensions : propriété de 2 objets qu'on peut imaginer coïncider exactement par des translations et des rotations dans le plan. Exemple 2 carrés de même côté, 2 tableaux occupés par les mêmes objets de la même manière. 2. À 3 dimensions : comme 1, sauf que les translations et les rotations peuvent se faire dans l'espace.

Graphes. Occupons chaque case par un point placé en son centre, chaque point est un sommet d'un graphe. S'il y a n cases, le graphe complet comprend n sommets, n(n-1)/2 arêtes, n(n-1) arêtes orientées.

Omino. Synonyme de tableau continu, lorsque sa forme est rectiligne ou en équerre. Le nombre de ses cases est v.

Par extension, on dira.

Fig. 5. Quelques ominos rectilignes, nombre de cases v = 1 à 9.

Domino. 1. Tablette rectangulaires dont la face porte 2 nombres compris entre 1 et 6, pour le jeu de même nom. 2. Jeu joué avec les dominos 1. 3. Tableau de 2 cases contiguës.

Monomino ou monoomino. Omino d'une seule case. Toute case isolée.

Polyomino. 1. Omino de plus de 2 cases. 2. - d'une case.

Triomino, quadriomino, cinqomino, sixomino etc. Voir omino, polyomino 1.

Les monominos sont tous congrus. Les dominos 3 sont tous congrus. Tout omino ayant plus d'une case peut prendre une forme rectiligne, verticale ou horizontale. Ces 2 dispositions sont congrues.

Omino rectiligne. Il est soit vertical soit horizontal. -vertical : toutes ses cases sont dans la même colonne.

-horizontal : toutes ses cases sont dans la même rangée. Figure 5.

Équerre. Supposons l'omino représenté par un point pour chaque case : un point est dit sommital ; il est accompagné soit à l'est soit à l'ouest par au moins un autre point qui est dit bras horizontal; il est accompagné soit au nord soit au sud par un point dit bras vertical. Les points tracent un angle droit.

Orientation d'une équerre. La direction pointée dans la rose des vents par le point sommital associé aux bras. Toute équerre a l'une de 4 orientations : NO, NE, SE, SO. Figure 6.

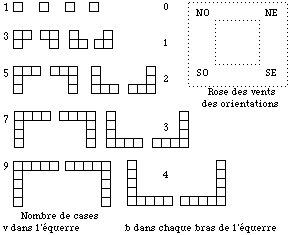
Fig. 6. Quelques équerres symétriques v = 1 à 9.

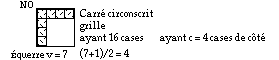
Fig. 7. Exemple d'un carré circonscrit à une équerre symétrique. Il est orienté NO comme l'équerre.

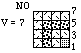
Fig. 8. Exemple d'un emboîtage orienté NO, V = 7. Il comprend 4 équerres : v = 7, 5, 3, 1.

Quadruplicité. On note cette propriété de quadruplicité des équerres, qui découle de la nature même de l'espace bidimensionnel.

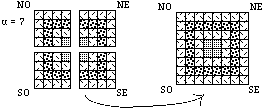
Fig. 9. Emboîtage global. Les 4 emboîtages orientés V = 7 forment un emboîtage global V = 7 qui a (7+1)2 = 82 = 64 cases.

Ominos et jeux de société. Les mouvements des pièces dans un jeu de dames ou d'échec se font entre les cases extrêmes de divers ominos dont certains sont des équerres. Pour le cavalier, c'est une équerre dissymétrique aux bras 1 et 2; pour la tour, c'est un omino rectiligne; pour le fou, c'est une équerre symétrique etc.

Équerre symétrique. Équerre ayant le même nombre b de points dans le bras horizontal et dans le bras vertical : b = (v-1)/2. Dans une équerre symétrique, on nécessairement b entier, v-1 pair et v impair. Une équerre symétrique a l'une des 4 oeientations, même si v = 1. Figure 6.

Circonscription. Une équerre symétrique v est circonscrite par une grille qui est un carré ayant c = b+1 = (v+1)/2 cases de côté et comprenant (b+1)2 = (v+1)2/4 cases. Le carré est orienté comme l'équerre. Figure 7.

Emboîtage orienté. Le carré circonscrit à une équerre d'au moins v = 3 cases peut recevoir plus d'une équerre. Dans ce cas, des équerres plus petites s'emboîtent dans celle-là. Disons que l'équerre la plus grande a V cases (V est un nombre impair).Voici les correspondances. Tableau 2, figure 8.

On remarquera dans le Tableau 2 que l'avant-dernière colonne, intitulée contenu, renferme le carré des nombres entiers successifs inscrits dans la 1re colonne. De plus, le contenu se décompose en une somme par équerre qui reproduit le Tableau 1 des nombres carrés.

Fig. 10. Emboîtages globaux du 1er au 5e. Progressions.

Etc

Emboîtage global. Pour chaque valeur de V, 4 emboîtages congrus entre eux, ayant respectivement les orientations NO, NE, SE, SO se réunisssent naturellement en accolant leurs équerres v = 1, formant un tableau ayant V +1 cases de côté et comprenant (V+1)2 cases. La géométrie conduit naturellement à quadrupler la somme des nombres carrés en suggérant le rassemblement de 4 emboîtages orientés, alors que l'arithmétique ne suggère rien de tel. Figures 9, 10.

Le format A4. Le format de papier A4, répandu en Europe, donne l'exemple d'un quadruplage et de son inverse, le pliage en 4, qui se sont imposés socialement pour des raisons de géométrie. Le format A4 résulte de 2 pliages en 4 successifs d'une feuille mesurant 1 m².

Progressions. Les emboîtages de la figure 10 présentent une double progression : arithmétique, de 1er terme 2 et de raison 2 pour le nombre de cases dans le côté 2c, arithmético-géométrique pour le nombre de cases (2c)².

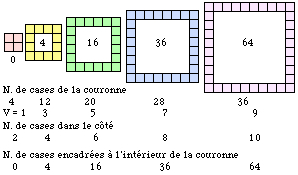
Fig. 11. Quelques couronnes. Les cases encadrées.

Fig. 12. 64 cases numérotées dans l'emboîtage global u = 7 ou dans une grille 8X8.

Dans un emboîtage global, le nombre de cases formant un côté est pair. Ce nombre, pour les valeurs successives de V, prend les valeurs 2, 4, 6, 8, 10... Le nombre correspondant de cases dans l'emboîtage global prend les valeurs 4, 16, 36, 64, 100... Figure 10.

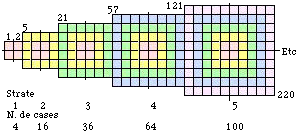
Fig. 13. Grille (système) du québécium. Les strates. On a marqué les quadrants et les couronnes concentriques. On suggère une numérotation des cases. À 2 dimensions.

Couronnes. En réunissant les 4 équerres symétriques v des 4 orientations, on réalise un tableau fermé dont le nombre de cases est un multiple de 4. Si v > 1, le tableau entoure des cases vides et il est une couronne v. Par extension, on appellera encore couronne le tableau de 4 monoominos v = 1, même s'il n'entoure aucune case vide. Figure 11.

Et encore : chaque emboîtage global après le 1er peut se décomposer en couronnes concentriques.

Numéroter les cases. Les cases d'un emboîtage global ont chacune leur individualité. On peut user de diverses conventions pour les discerner. Le plus immédiat est de procéder à la manière de l'écriture sur un papier ligné, par lignes et retours à la ligne. Figure 12.

Dans les applications, nous allons exploiter la figure 10 en associant ses emboîtages à peine modifiés et en délaissant le vocabulaire géométrique utilisé jusqu'ici.

Nous adoptons le nom de grille du québécium (ou encore, de système du québécium) pour l'association des emboîtages globaux successifs accolés, que nous appellerons des strates. La grille la plus utile a 4 strates. Chaque strate s'analyse en quadrants NO, NE, SO, SE qui sont les emboîtages orientés et en couronnes. Les cases peuvent se numéroter selon les principes plus haut. Figure 13.

Tout ceci à 2 dimensions.

Précédent QbSyst2e.2.html

Début QbSyst2e.1.html