Système du Québécium

Cases losanges. En créant un tableau ou une grille, nous pouvons choisir des colonnes obliques au lieu de verticales. En choisissant une inclinaison de 30^o de l'axe vertical NS, les cases deviennent des losanges composés de 2 triangles équilatéraux. Équerres, emboîtages et couronnes sont altérés de façon correspondante. Les diagonales NO SE et NE SO, diagonales d'un losange, ne sont plus à 45^o de la verticale mais restent mutuellement à angle droit. C'est un cas d'homothétie. Figure 14.

Cases circulaires. Cette transformation se visualise commodément si les cases sont circulaires. L'arrangement de symétrie carrée devient de symétrie hexagonale. Un cercle qui en touchait 4 en touche 6. Figure 15.

Occupation de l'espace. Avec des cases circulaires, nous cessons d'occuper jointivement l'espace puisque ces cases laissent nécessairement des vides entre elles. Il subsiste néanmoins la notion d'occupation discontinue de l'espace, la position d'un point figuratif à l'intérieur du cercle étant indifférente. Les points situés entre les cercles sont dénués de sens. On peut imaginer une contraction des points occupant l'espace d'un carré, les amenant à se loger dans un cercle et laissant vide une portion de l'espace .

Cellule. Le terme et la notion de cellule d'occupation discontinue de l'espace peuvent rendre service, pouvant s'appliquer aux cases en forme de carré, de losange et de cercle.

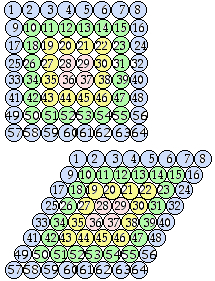
Fig. 15. Cases circulaires. Homothétie de la grille, qui devient un losange. La case circulaire 10 touchait 4 cases : 2, 9, 11, 18; elle en touche maintenant 6 : en outre 1 et 19.

On peut ajouter une dimension munie d'une succession de cases à un tableau bidimensionnel et appeler le résultat un tableau tridimensionnel. Dans le cas le plus simple, sur chaque case carrée on empile des cubes, les cases planes sont remplacées par des cellules cubiques et la grille 3D est elle-même un cube, empilement régulier de cubes. Figure 16.

Cellule. L'équivalent, à 3 dimensions, d'une cellule à 2 dimensions; peut être cubique et peut faire place à une sphère.

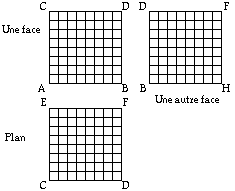
Fig. 16. Un tableau tridimensionnel de 8X8X8 = 256 cellules.

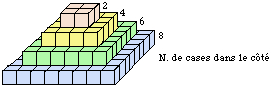
Fig. 17. 4 emboîtages figure 7 devenus pyramide à base carrée.

Pyramide à base carrée. Un passage de pseudo à véritable tridimensionnalité se présente naturellement. Dans la figure plane 7, nous plaçons un cube sur chacune des cases des emboîtages. La répartition des cubes est bidimensionnelle mais ils ont chacun une épaisseur. Nous superposons maintenant les emboîtages, le plus grand au bas et nous obtenons une pyramide à base carrée qui occupe 3 dimensions. Figure 17.

Cases sphériques et forme losange. Un autre cas de pseudo-tridimensionnalité nous intéresse. Nous accordons une épaisseur, 3e dimension, aux cases d'une grille bidimensionnelle. Les cases deviennent par exemple des cubes ou des sphères répartis selon 2 dimensions.

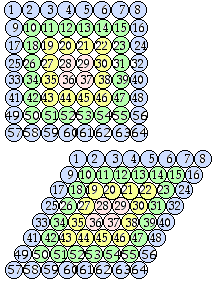
Fig. 18. Des boules et non des cercles : un tableau pseudo-tridimensionnel de 64 cases. La grille carrée devient un losange comme à une figure précédente.

Puis nous passons à la forme losange. La figure nouvelle a exactement l'aspect de la figure 15, mais les cercles se rapportent à des boules vues d'aplomb. Il n'est pas difficile de concrétiser cette figure en utilisant un assemblage de boules maintenues en place par des règles. Figure 18.

Repli. Nous procédons, sur le tableau losange, à des déplacements amenant certaines boules à se placer au dessus des autres. Le résultat est un tableau à 3 dimensions vraies. Le repli d'une feuille plane infiniment mince n'ajoute pas une dimension. Autrement en est-il ici.

Le losange possède une petite diagonale NO SE traversant les boules 1, 10, ... 55, 64, définissant 2 parties dans l'assemblage : partie ouest 40 boules, partie est 24 boules.

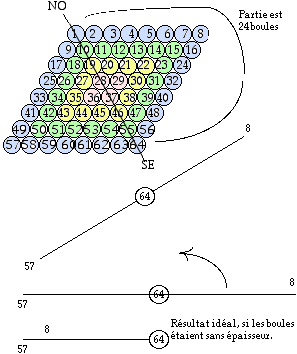
Fig. 19. On fait tourner (hors du plan) la partie est autour de l'axe NO SE. La boule 8 se loge sur les boules 49, 57, 58.

Dans la présente opération de repli, les boules de l'enfilade 2 à 56 restent au contact de celles de l'enfilade 1 à 64 . Toutes les boules de la partie est finissent par se placer chacune au contact de 3 boules de la partie ouest, en équilibre stable. Les étapes se comprennent figure 19, 20, 21. La partie est compte 24 boules qui, après rotation dans le plan, se placent sur 24 vides de la partie ouest.

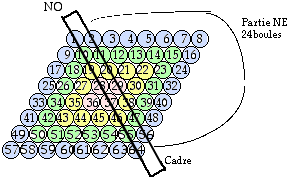
Fig. 20. Dans le repli décrit, il doit y avoir glissement de l'enfilade des boules 2 à 56 au contact de l'enfilade des boules 1 à 64. Un cadre rigide doublement articulé à 2 broches traversant ces enfilades assure le respect de cette condition.

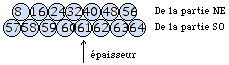
Fig. 21. Vue en élévation de la superposition tridimensionnelle.

Ainsi apparaît un tableau tridimensionnel à 2 étages. Il dessine un tronc de tétraèdre régulier et cela se rattache à la théorie de l'empilement des oranges.

Cela pour un tableau de 64 boules. S'il n'y a que 4 boules, le repli assurant le passage de pseudo à proprement tridimensionnel est plus aisé à comprendre. Figure 22.

En général, un processus de repli appliqué à un tableau de boules pseudo-tridimensionnel carré devenu losange fait apparaître un tronc de tétraèdre régulier. Les résultats sont rassemblés pour 2, 4, 6 et 8 boules de côtés. Figure 23.

Axes doublement obliques. Dans les empilements dessinant des tétraèdres réguliers, les centres des boules se placent à intervalles unités selon des axes de coordonnées triobliques.

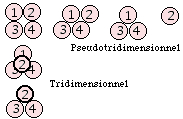
Fig. 22. Tableau de 4 boules. Tétraèdre résultant de sommets 1, 2, 3, 4. Ici le tronc de tétraèdre est un tétraèdre.

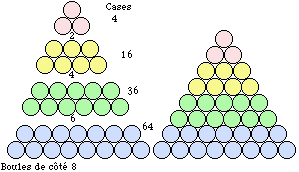
Fig. 23. Les troncs de tétraèdres provenant de tableaux losanges ayant 2, 4, 6 et 8 boules de côté. La réunion de ceux-ci, dessinant un tétraèdre de 120 boules ayant 8 boules de côté. Vue latérale.

Rose des vents 3D. La rose des vents de 4 points cardinaux doit se compléter, dans un tableau tridimensionnel, par un zénith et un nadir. Les 6 directions ainsi définies forment entre elles, selon les axes choisis, des angles droits ou obliques.

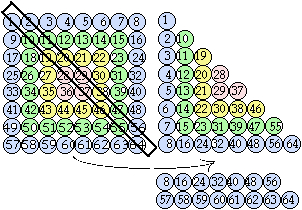
Fig. 24. Repli d'un tableau carré de 8 boules de côté. Le résultat, vue en plan. Les boules d'un étage masquent certaines boules de l'étage inférieur. Vue de côté.

Graphes 3D. Qu'un tableau soit pseudo- ou proprement tridimensionnel, qu'il ait subi ou non des replis, le nombre de sommets du graphe, égal au nombre des cases ou des cellules, reste le même. Semblablement pour les arêtes. Par exemple, dans le tableau tétraédrique de la figure 23, le graphe complet comprend 120X119 = 14280 arêtes orientées.

Repli et continuité. Le processus de repli ci-dessus conduit à remplacer un tableau de boules par 2, occupant 2 étages par une continuité d'un seul tableau. On déclare qu'un étage se continue dans l'autre, un peu comme un tapis qu'on plierait sur lui-même, disons les touffes en dedans. La surface extérieure est l'origine de l'épaisseur, des touffes se font face. Les lieux à l'intérieur du repli ont doubles coordonnées.

Dans une conception analogue qui sert en géographie, on décrit un lieu terrestre par longitude, latitude et altitude au dessus du niveau de la mer. La surface d'altitude zéro est courbe. Les lieux d'altitude négative ont doubles coordonnées, au point d'émerger aux antipodes.

Fig. 25. Voici comment un tableau de 16 boules carré devient un losange puis se replie pour occuper 2 étages.

La cellule élémentaire du réseau de coordonnées est alors un cube déformé de telle sorte que ses faces deviennent des losanges formés de 2 triangles isocèles. Cette cellule est celle du système trigonal en cristallographie : elle pave l'espace.

Pavage. Propriété qu'ont certaines figures de remplir l'espace par leur répétition sans interstice et sans chevauchement. Ainsi le triangle équilatéral pour l'espace plan, le cube pour l'espace tridimensionnel.

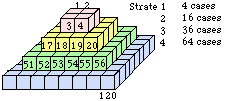
Fig. 26. Pyramide du québécium. 4 strates. Numérotation partielle des cases. Cases cubiques.

Fig. 27. Tétraèdre du québécium. 4 strates. Numérotation partielle des cases. Cases sphériques.

Repli d'un tableau carré. Tout tableau pseudotridimensionnel carré de boules se prête à un repli comparable à celui décrit pour le tableau losange. On a avantage à utiliser un cadre de 2 broches parallèles. Les boules de la partie NE se placent chacune au dessus d'une boule de la partie SO. Leur équilibre est instable. Figure 24.

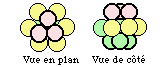
Fig. 28. 12 boules autour d'une seule.

Fig. 29. Le losange du rhombododécaèdre pavant.

Dans les applications, nous allons exploiter la grille du québécium devenue tridimensionnelle, par une mise en forme des figures 17 et 24. Nous persisterons à l'appeler grille et tableau, malgré le passage de 2 à 3 dimensions, mais nous utiliserons plutôt des désignations nouvelles pour éviter la confusion. Grille et système du québécium s'entendent de préférence à 2 dimensions, pyramide et tétraèdre sont à 3 dimensions. Nous limitons à 4 strates et 120 cases.

Pyramide du québécium. Nous reprenons la figure 17 et nous numérotons les cases d'après le schéma du système 2D de la figure 13. Les cases sont des cubes et forment des étages méritant le nom de strates vu leur étagement. Cette pyramide est à base carrée.

Tétraèdre du québécium. Nous reprenons la figure 23. Des strates et des numéros comme dans la pyramide du québécium mais les cases sont sphériques. La numérotation se fait selon la continuité du repli figure 24. Ce tétraèdre est régulier et il est une pyramide à base triangulaire.

Pavage du tétraèdre. Le rhombododécaèdre pavant. Le tétraèdre ne pourrait-il pas être pavé par de petits tétraèdres? La réponse est non. Nous pouvons échafauder des petits tétraèdres. chacun reposant sur les sommets de 3 autres, mais il reste des espaces vides (lesquels sont des octaèdres). Mais ce n'est pas là un pavage. Le seul solide régulier se prêtant au pavage est le cube, qui ne convient pas ici.

Un solide est un corps à 3 dimensions limité de toutes parts par des faces planes. Il est régulier s'il ne renferme qu'une sorte de faces, d'arêtes et d'angles dièdres et polyèdres.

Peut-il être pavé par un autre solide? La réponse est oui.

Une sphère à l'intérieur du tétraèdre est en contact avec 12 autres : 6 alentour en couronne, 3 en dessous, 3 au dessus, total 12. Figure 28.

Par chaque point de contact on fait passer un plan tangent et cela fait 12 plans qui se coupent selon des arêtes d'intersection : nous avons engendré un dodécaèdre pavant pour le tétraèdre régulier. Il existe par ailleurs une infinité de rhombododécaèdres non pavants pour le tétraèdre régulier. Apparemment, cette figure n'a été remarquée que lors de l'étude des empilements d'orange, vers l'an 1650. C'est le rhombododécaèdre à faces losanges, les diagonales de ces losanges étant dans le rapport de 1 à ˆ2 = 1,41421... Figure 29.

Au lieu des cellules sphériques dans le tétraèdre du québécium, nous pouvons installer des cellules en forme de rhombododécaèdres. Les cellules sphériques sont plus faciles à dessiner et à manipuler. On ne trouve pas d'objets ayant la forme nécessaire dans le commerce. Il ne faut pas confondre avec le dodécaèdre régulier aux faces pentagonales.

L'emploi, réel ou imaginé, de cellules en forme de rhombododécaèdres fait disparaître le problème des espaces vides entre cellules sphériques.

Un cube remarquable. La 4e strate renferme 64 cases, sous la forme de carrés dans la grille du québécium, de cubes dans la pyramide. Ces 64 cases peuvent encore s'agencer pour donner un cube ayant 4 cases de côté : le cube du québécium. Cela tient à ce que 64 est à la fois le cube et le carré d'un nombre entier. C'est le plus petit nombre doué de cette propriété. Le nombre suivant doué de la même propriété est 729, carré de 27 et cube de 9.

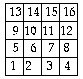
Fig. 30. Le cube du québécium. 64 cases cubiques. Vue d'une face avec une numérotation possible des cases visibles.

La numérotation des cases dans le cube du québécium pose d'intéressants problèmes.

Autres formes tétraédriques. L'échafaudage de boules semblables en nombres multiples de 4 permet de réaliser des structures ayant les symétries du tétraèdre régulier. C'est particulièrement vrai pour des nombres égaux à 16, 20, 36, 56, 64. Les boules peuvent être remplacées par les rhombododécaèdres décrits.

La théorie des ominos a fait apparaître des tableaux remarquables, bi- et tridimensionnels, reliés à la théorie arithmétique des nombres carrés, comme suit.

À 2 dimensions, la grille du québécium.

À 3 dimensions : la pyramide du québécium, le tétraèdre du québécium.

Nous allons voir que ces tableaux sont remarquablement adaptés à la classification des biomolécules et des éléments. Nous essayerons de comprendre pourquoi il en est ainsi.

Ils sont à la base mathématique du système du québécium. Figures 13, 26, 27

Précédent QbSyst2e.3.html

Début QbSyst2e.1.html