Analyse.

Essayons d'imaginer une organisation au niveau atomique correspondant aux accords que voilà. Le modèle nécessaire est aussi bien virtuel que la théorie du spin de l'électron elle-même. Je l'appellerai géométrique, ou géométrico-atomique.

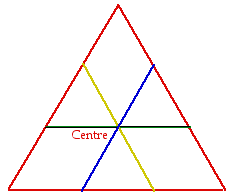
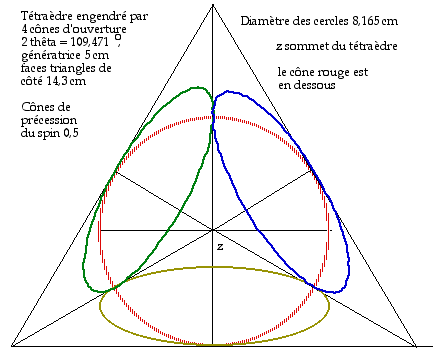
Le spin de l'électron : I = 1/2 = I'. Les spins de quatre électrons dans un atome ont une tendance à grouper leurs cônes de précession avec une origine et une génératrice communes à deux cônes. On suppose ici les cônes impénétrables comme la matière ordinaire est impénétrable. Figs 1, 2.

Fig. 1. Quatre cônes, un tétraèdre. GQAfig. 4.gif.

Fig. 2. Cônes impénétrables (les cônes ont une génératrice en commun), cônes pénétrables (un cône a une génératrice en coïncidence avec l'axe de l'autre) . On montre la base des cônes. Au lieu d'imaginer des cônes se compénétrant, il est équivalent d'imaginer des cônes ayant l'ouverture angulaire moitié.

On peut voir de cela une confirmation dans l'importance des symétries 4, nécessaires pour expliquer la classification des éléments chimiques. Un appui récent provient d'un examen des atomes irréguliers. http://www.lisulf.quebec/Irr%8eguliers22.html

La tétravalence du carbone. Les 4 valences du carbone sont rigoureusement équivalentes chimiquement, malgré qu'elles appartiennent selon la spectroscopie à 2 électrons 2s et 2 électrons 2p. L'explication est immédiate dans le présent modèle. Il faut supposer que les forces qui déterminent l'association selon les 4 cônes uniformisent le comportement des 4 électrons de valence. Les équations d'état de Schrödinger mettent en algèbre cette égalité mais ne la justifient pas.

L'explication encore acceptée aujourd'hui remonte à Linus Pauling. "Pauling introduit notamment le concept d’hybridation des orbitales atomiques. Alors que les électrons dans les atomes sont décrits par des orbitales s, p, (…), il montre que pour décrire les liaisons au sein des molécules il est préférable de construire des fonctions qui sont des mélanges de ces orbitales. Par exemple, les orbitales 2p et 2s d’un atome de carbone peuvent se combiner pour former quatre orbitales équivalentes (appelées orbitales hybrides sp3) qui permettent mieux de décrire des composés comme le méthane, à géométrie tétraédrique. " http://www.amessi.org/Parcours-de-Linus-PAULING

(Voyez Référence 2, AMESSI et Linus Pauling.)

Voici du même auteur ibidem au sujet de la structure du benzène, établissant une similitude entre hybridation et résonance. "Ce phénomène sera plus tard baptisé du nom de résonance. D’un certain côté, ce phénomène est analogue à celui d’hybridation des orbitales atomiques, puisqu’il consiste en la combinaison de plusieurs structures électroniques ."

On trouve un exposé sur l'hybridation sp3 du carbone. http://fr.wikipedia.org/wiki/ Hybridation_(chimie)

On trouve un exposé en termes de 4 fonctions d'onde. Les auteurs leur imposent d'avoir toutes la même forme géométrique et obtiennent pour la molécule de méthane CH4 (leur fig. 10) une figure où "les quatre atomes d'hydrogène forment les sommets d'un tétraèdre régulier dont l'atome de carbone est le centre". Mécanique quantique pp. 865-6, Tome I, Cohen-Tannoudji, Diu et Laloë. 1973 et 1998, Hermann, ISBN 2 7056 6074 7

L'intervention proposée dans le présent travail, des cônes de précession des spins des 4 électrons, fournit une explication à ce que les 4 fonctions d'onde aient toutes la même forme géométrique. Il n'est plus nécessaire d'imposer cette condition, il suffit d'admettre qu'elle découle de la géométrie des 4 cônes saturant l'espace des angles solides. La géométrie des spins s'impose plutôt que celle des moments cinétiques orbitaux avec l = 1 et l =0.

Je propose que la liaison est très forte dans le coeur de l'atome de carbone, qui est un hélioide de charge 6 au lieu de 2. À témoin, le potentiel de première ionisation de l'atome He et le plus grand de tous les éléments ( 24,4 e. v.). Dans l'hélioïde, il est multiplié par le carré du rapport 6/2 Il est attrayant d'attribuer à cette force l'indépendance de comportement des 4 autres électrons, devenant libres d'obéir aux forces modestes liées au présent modèle. Nulle part plus loin dans le tableau des éléments chimiques rencontre-t'on une liberté égale et ce serait le secret de la richesse de la chimie organique et de la vie.

Les fermions. Les valeurs I = I' = 1/2 ne sont pas l'exclusivité des électrons. On admet que tous les fermions, sujets à la statistique de Fermi-Dirac, ont un spin ou moment cinétique propre égal à 1/2 ou à une autre valeur semi-entière, et qu'ils ont une tendance, lorqu'ils interagissent comme c'est le cas à l'intérieur d'un atome ou d'une molécule, à se trouver chacun dans un état différent. Cette tendance s'accorde avec l'incapacité du tétraèdre à daller l'espace : si des électrons sont contraints à voisiner dans l'espace géométrique, ils garderont leur nature propre qui les empêche de procéder au dallage, mais du moins se créeront-ils des cellules virtuelles distinctes dans un espace de configuration : par exemple celles dont la formule du québécium donne la liste.

Électrons atomiques l = 0. Certains électrons dans les atomes sont privés de moment cinétique orbital. ce sont 16 électrons s, qui servent d'électrons de valence dans les 16 alcalins et alcalino-terreux et qui terminent les 4 strates et les 8 périodes : H. He, Li, Be, Na, Mg, K, Ca, Rb, Sr, Cs, Ba, Fr, Ra. Uue. Uub. Ces 16 électrons ont comme momnt cinétique leur seul spin moment cinétique propre. Dans le présent modèle, on voit très bien qu'ils correspondent à 4 tétraèdrs distincts.

Spin du photon : I = 1, I' = 1. On admet que tous les bosons ont un un spin égal à l'unité ou à un autre nombre entier et le photon est un boson auquel on attribue le spin 1. L'aptitude du cube à daller l'espace s'accorde avec la tendance des bosons à obéir à la statistique de Bose-Einstein et à occuper tous le même état lorsque plusieurs d'entre eux interagissent. Le laser présenterait une concrétisation de la géométrie du cube dans le domaine atomique. Le laser est un succès de la théorie de la relativité et de l'émission stimulée auxquelles on attache les noms de Poincaré et d'Einstein. La lumière est le domaine où l'unification relativiste de l'espace et du temps s'est manifestée pour la 1re fois. - Cela rattache notre géométrie platonicienne d'autant à la théorie de la relativité.

Électrons atomiques l = 1. Dans les atomes p, l'électron de valence a un moment cinétique orbital I = 1. La formule du québécium donne leur liste : ils sont 36, soit 12 dans chacune des strates 2, 3 et 4, càd 6 dans chacune des périodes 3, 4, 5, 6, 7 et 8.

Il faut admettre que les électrons de valence p aient invariablement l = I' = 1 dans notre modèle. Ils correspondent dès lors à 6 cubes. Jusqu'ici et en mettant de côté les 68 éléments de transition d et f, on peut alors établir un tableau géométrico-atomique de 52 éléments tous réguliers, en 4 tétraèdres et 6 cubes. Appelons-le platonicien. Chaque strate renferme un tétraèdre; chaque strate après la 1re renferme 2 cubes.

L'écriture des éléments du 1er tétraèdre est consécutive, l'écriture des éléments dans chaque tétrade suivante se fait en 2 temps, comme suit.

• 1re strate

1er tétraèdre (H, He, Li, Be)

• 2e strate

• 3e strate

• 4e strate

<><><><><>

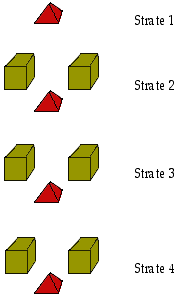
Fig.4. Tableau platonicien des 52 éléments s et p. platonicien52.gif

Octaèdre. Les atomes d ou l = 2 se présentent en 8 demi sous-couches de 5 chacune dans les strates 3 et 4. Or avec 8 atomes d ayant chacun une projection 2, I = I' = 2, on obtiendrait un octaèdre, ce qui suggère que les électrons et les atomes d auraient une tendance à se grouper par 8 pour raisons de symétrie, soit 4 dans chaque demi sous-bloc. On pourrait rattacher à une compétition entre ces deux tendances la présence d'irrégularités, qui sont au nombre de 10 parmi les 40 éléments d.

Les demi sous-blocs d : 5 éléments sont observés

..........................................4 éléments sont suggérés par le modèle de l'octaèdre

Une conciliation est-elle possible? Voici une tentative.

La colonne vertébrale. Il se trouve que, pour des raisons liées à l'observation expérimentale et à la symétrie, distinctes du présent modèle géométrique, le système du québécium propose la présence d'une colonne vertébrale qui contient tous les éléments dont les demi sous-couches sont complètes. Dans cette colonne vertébrale, on n'observe aucun élément irrégulier, et cela tient évidemment à ce que les moments cinétiques orbitaux des Z électrons de ces atomes forment une structure saturée, se combinant pour donner une somme vectorielle nulle, aussi bien qu'un atome s, l = 0 d'alcalin ou d'alcalino-terreux, pour cause de saturation des valeurs possibles du quantum magnétique m.

Dans la colonne vertébrale d, somme l indice i, i = 1 à Z = L = 0 pour Z = 25, 30, 43, 48; 73, 80, 107, 112.

Cela nous donne des raisons de distinguer deux catégories d'éléments d. dans chacune des 8 demi sous-couches d, chacune renfermant un élément L = 0 et 4 autres, et ce nombre 4 s'accorde avec le modèle de l'octaèdre. Il apparaît 4 octaèdres.

Un tableau met en vedette les éléments hors colonne vertébrale, dont les 32 éléments d, voyez http://www.lisulf.quebec/Irr%8eguliers22.html Figs 8, 9, 12

Ce tableau est repris ici avec simplifications. Fig.5

Fig. 5. Les éléments d et f, la colonne vertébrale.

Rhombododécaèdre. Il semble qu'il y ait une situation comparable pour les 28 atomes f, l = 3. Notre modèle suggère que 12 électrons l = 3 pourraient se grouper afin de donner un rhombododécaèdre. Or les atomes f forment des sous-couches de 14. La compétition entre les deux tendances, à réaliser les structures 12 et 14, pourrait expliquer la présence d'irrégularités, au nombre de 9 parmi les 28 éléments f.

Les demi sous-couches f : 7 éléments sont observés

..............................................6 éléments sont suggérés par le modèle du rhombododoécaèdre

La conciliation se fait comme celle des éléments d, pour les 4 demi sous-couches f.

Dans la colonne vertébrale f, somme l indice i, i = 1 à Z = L = 0, i = 1 à Z, Z = 63, 70, 95, 102. Voyez Fig. 5 et encore voyez http://www.lisulf.quebec/Irr%8eguliers22.html Figs 8, 9, 12

Ces 4 éléments sont ainsi exceptés, et il reste deux sous-couches de 12 hors colonne vertébrale, qui satisfont à la confection de 2 rhombododécaèdres.

Solides homoédriques. Il est intéressant de constater que deux polyèdres homoédriques jouent des rôles en tous points comparables à l'égard des deux strates consécutives 3 et 4, quoique l'un d'eux soit platonicien (l'octaèdre) et l'autre pas (le rhombododécaèdre). Cela confirme la pertinence d'agrandir oo catégorie platonicienne, après des siècles de restriction, et de porter attention à la catégorie des solides homoédriques.

On a coutume de reconnaître 4 catégories d'éléments chimiques d'après le caractère de leur électron de valence, selon qu'il est de moment cinétique orbital 0, 1, 2 ou 3, soit s, p, d ou f. La discussion du paragraphe précédent suggère que 8 atomes d et 4 atomes f se rattachent à 2 égards, aux atomes s, quoique leur électron de valence ne soit nullement s. 1o Ils sont systématiquement réguliers, se plaçant dans la colonne vertébrale; 2o ils ne répondent pas au modèle de l'octaèdre ou à celui de rhombododécaèdre destinés aux atomes d et f. Pour chacun d'eux, la somme des moments cinétiques orbitaux S de l'atome est nulle. Afin de leur attribuer une catégorie géométrique à eux aussi, puisqu'ils sont laissés pour compte des deux dernières catégories géométriques mentionnés, on les rattachera aux alcalins et alcalino-terreux avec leurs 4 tétraèdres s, et on leur attribuera 3 tétraèdres, marqués S .

Ce qui précède permet donc d'écrire un tableau des éléments en solides géométriques représentant chacun, selon le cas, 4, 6, 8 ou 12 éléments. L'écriture des éléments se fait en 2 temps dans plusieurs de ces solides. Trois solides platoniciens et un homoédrique qui n'est pas platonicien y apparaissent : le tétraèdre, le cube, l'octaèdre, le rhombododécaèdre.

Un tableau restreint aux 16 éléments s figurés par 4 tétraèdres et aux 36 éléments p, représentés par 6 cubes est à la Fig. 4.

Voici maintenant un tableau complet, ajoutant au précédent 3 types de solides représentant les éléments d et f. La description suit et l'image est à la Fig. 6. Un octaèdre représente 8 éléments d, un rhombododécaèdre représente 12 éléments f, un tétraèdre S représente 4 éléments d ou f dont les demi sous-couches sont saturées.

---------

---------

Fig. 6. Tableau platonicien des éléments. platon120.gif En bref, les correspondances suivantes apparaissent entre les moments cinétiques 1/2, 1, 2 et 3 respectivement et les solides tétraèdre, cube, octaèdre et rhombododécaèdre. Voyez Fig. 8.

Le dodécaèdre et l'icosaèdre correspondraient à un moment cinétique I = 4, projection I' = 4. Ce moment cinétique n'a pas de réalisation dans les atomes au repos. Voyez Fig. 7 la feuille de calcul concernant les cônes de précession des divers moments cinétiques parmi lesquels ceux du dodécaèdre et de l'icosaèdre.

Les solides de Platon aux angles dièdres convexes sont indubitablement au nombre de 5. On a des raisons d'ajouter le rhombododécaèdre régulier, ce qui totalise 6 solides homoédriques. En admettant les angles dièdres concaves, on obtient 5 solides coiffés et le total devient 11 solides réguliers.

Pour obtenir les solides coiffés, on a manipulé le solide original en agissant sur ses faces, la manipulation consistant en une prolongation des faces sans altération des angles mutuels dièdres qu'elles forment. Cette prolongation des faces est accompagnée d'une prolongation des arêtes segments de droites rencontres des faces. Ces rencontres, ne déterminent pas d'angles dièdres de valeurs nouvelles; en revanche, les angles polyèdres à la rencontre de plus de 2 faces prolongées ont des ordres nouveaux, par exemple l'ordre 6 en plus de l'ordre 3, quand on passe du dodécaèdre régulier au petit dodécaèdre étoilé qui en dérive.

La manipulation décrite au paragraphe précédent appartiendait-elle à une catégorie plus générale de manipulations sur un solide? Convenons de conserver le caractère essentiel à l'identification du solide qu'est l'angle dièdre à la rencontre de 2 faces. La catégorie qui apparaît contient alors, outre la prolongation des faces, leur déplacement par translation. Appelons cette catégorie dérivation et disons que dérivation contient prolongement et translation

La dérivation par prolongement conduit aux formes étoilées et s'appelle stellation. Quel est le résultat dérivant de la translation? Sauf contraintes imposées, le résultat est multiple et contient par exemple les parallélipèdes si l'on agit sur un cube.

Procéder à des translations ou à des prolongements des faces : dans les deux cas, les angles dièdres originaux se conservent.

Imposons des contraintes de la façon que voici.

À chaque face nous gardons ses dimensions et ses angles plans. Nous la déplaçons d'un mouvement rectiligne en amenant son centre au centre de figure du solide donné. Voici le résultat pour quelques solides.

1. Tétraèdre régulier. Quatre triangles ayant intersection deux à deux, qui morcellent chaque face en 9 triangles équilatéraux. Le volume fermé par ces triangles est nul, ils dessinent 14 cellules de 3 sortes ayant toutes un sommet au centre et formées de triangles équilatéraux ::

4 sont triangulaires et ont pour faces 3 triangles;

4 sont sont triangulaires et pour faces 3 losanges équilatéraux;

6 sont quadrangulaires et ont pour faces 2 triangles équilatéraux et 2 losanges équilatéraux.

On remarque la manifestation de symétries 3 et 4, en accord avec les nombres entiers impliqués 2 et 3.

Tous les sommets sont simples, d'ordre 1. Ils sont ceux d'une surface de dimension 2 : ce sont des surfaces n'ayant qu'un côté.

L'objet obtenu s'inscrit dans un tétraèdre dont le côté vaut les 4/3 de celui du tétraèdre original

1bis. Surface n'ayant qu'une face. Surfaces anti-Möbius. On est confronté à certains exemples de surfaces où l'on peut passer sans discontinuïté d'une face à son opposée, du type Möbius. Elles sont développées dans 3 dimensions et elles ont des portions courbes. La présente analyse nous place devant un cas opposé, où apparaît une surface bidimensionnelle plane limitée n'ayant qu'une face et où, par hypothèse et construction, on n'a aucun moyen de passer à la face opposée. On pourrait l'appeler surface anti-Möbiüs. Non seulement est-il impossible de passer à la face opposée, mais encore celle-ci est inexistante., Elle n'apas d'existence.

Au lieu de parler d'existence, on pourrait parler de visibilité : la surface serait visible d'un côté mais non de l'autre. Voici des exemples. Les vitres permettant d'observer sans être vu; la transmission d'images par télévision, le spectateur voyant le programme sans être vu; plus généralement, l'information d'une photo ou d'un portrait se transmet de sa source vers le spectateur mais non en sens inverse. Enfin, la flèche du temps fait que l'information se transmet du passé au futur.

1ter. Un aspect philosophique. Ce caractère ajoute à la singularité du tétraèdre régulier, que le présent travail rattache aux fermions, particules remarquables par l'individualité de chacune d'entre elles.

2. Cube. Le résultat final est l'intersection de 3 carrés mutuellement perpendiculaires, formant un trièdre trirectangle de 8 cellules qui sont des octants, où tous les angles dièdres sont des droits 90o. Les faces opposées parallèles en se rapprochant finissent par se confondre 2 à 2 en déterminant un solide d'épaisseur nulle ayant 2 faces; les angles dièdres aux arêtes valent 180o. Les angles polyèdres aux sommets sont simples et d'ordre 1 puisqu'ils appartiennent vraiment à des portions de plans et on peut y reconnaître l'ordre 2 puisque ces portions de plans proviennent de deux plans initialement distincts et devenus virtuels. Il y a une certaine continuïté virtuelle d'une face à la face opposée, à la différence du cas du tétraèdre.

3. Rhombododécaèdre régulier. Les 12 faces sont transportées de façon à contenir le centre du solide, se confondant 2 à 2, elles déterminent 6 plans passant par le centre. Ces plans sont perpendiculaires 2 à 2 et déterminent à eux deux un angle dièdre 90o nouveau pour le RBD. Cet angle est présent dans le RBD, pas comme dièdre à l'intersection de deux faces, mais à la rencontre ponctuelle de deux faces aux sommets 4.

On peut procéder de semblable façon pour les 8 autres solides réguliers énumérés plus haut, y compris les solides étoilés.

Ainsi apparaissent 11 solides nouveaux dérivés par la sorte de translation décrite. à partir des 11 solides réguliers énumérés plus haut.

Ces solides nouveaux ont cette particularité de ne comprendre que des surfaces et de ne fermer aucun volume. On pourrait les appeler solides sans volume ou solides privés (privés de volume). Le tétraèdre sans volume, le cube sans volume etc. Il semble aussi légitime de parler de solides réguliers pour ces "solides sans volume" que pour les "solides coffés" quand on commença à examiner ces derniers. La liste des solides réguliers en comprend donc 22.